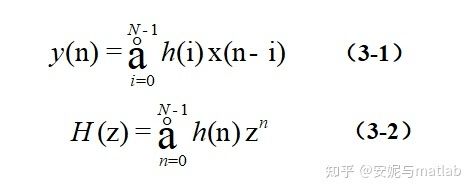基于matlab的语音信号滤波处理

基于matlab的语音信号滤波处理

摘要：本课程设计的主要目的是在MATLAB环境下，使用窗口设计法设计一个滤波器，并对语音信号进行滤波去噪。开发平台为MATLAB，设计方法为窗口设计法。用麦克风采集一段语音信号，绘制波形并观察其频谱，给定相应技术指标，用凯塞窗设计一个满足指标的FIR滤波器，对该语音信号进行滤波去噪处理，比较滤波前后的波形和频谱并进行分析。在滤波前后语音信号波形的变化中，由于我们录制的语音信号噪声不大，所以观察并不明显，但在频域波形中，我们可以明显的看到设计的滤波器对语音信号进行了滤波处理，将噪声进行了滤除。此次滤波基本达到了要求，完成了设计指标。

关键词：滤波去噪；FIR滤波器；凯塞窗；MATLAB

目录

1 课程设计研究内容 1

1.1课程设计研究内容 1

1.2课程设计步骤及流程图 1

1.3课程设计要求 3

2 设计原理 3

2.1 MATLAB简介 3

2.2 滤波器 3

3 设计与实现过程 3

3.1实现方法 3

3.1.1 FIR滤波器 4

3.1.2窗口设计法 4

3.1.3凯塞窗 4

3.2 设计过程 4

3.2.1录制语音信号 4

3.2.2 对原信号加入噪声 5

3.2.2 滤波器的设计 7

3.2.2信号的滤波处理 9

3.3 仿真结果与分析 10

4 调试问题与解决方案 11

5总结与展望 11

致谢 12

参考文献 12

附录 12

附录1. 滤波器脉冲响应源程序 12

附录2. 理想低通滤波器计算源程序 13

1 设计研究内容

1.1设计研究内容

1.语音信号的采集

在Windows下录制一段格式为.wav的语音，利用函数wavread对语音信号进行采样。

2.语音信号的频谱分析

用MATLAB程序对原始语音信号进行采样、频谱分析，并绘制出采样后语言信号时域波形图和频谱图，并针对此图分析语音信号特点。

3.语音信号加噪与频谱分析

利用MATLAB程序产生信号噪声，并加入到语音信号中，模仿语音信号被污染，并对其频谱分析，与原始语音信号进行对比，分析差异。

4.设计数字滤波器

根据语音信号的特点，设计数字滤波器，对加噪后的语音信号进行滤波处理。

5.验证滤波器的滤波效果

对滤波后的语音信号进行时域、频域分析，并将滤波前后的时域波形、频谱波形进行相比较，分析信号的变化，从而验证所设计滤波器的滤波效果是否达到了滤除高频噪音、保留低频原始语音信号的目的。

6.回放语音信号

利用函数sound对滤波后语音信号进行回放。

1.2设计步骤及流程图

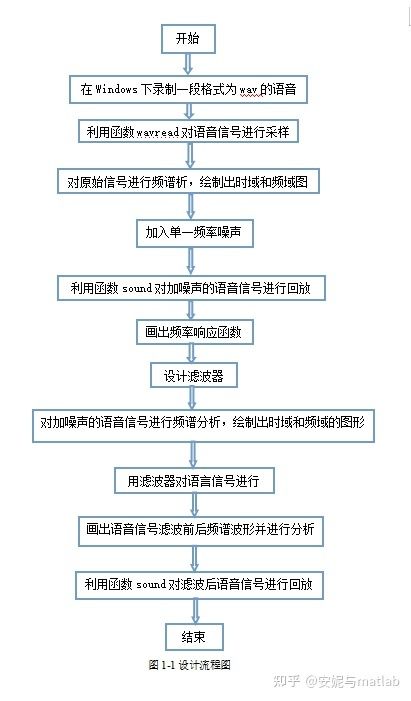
设计本课题的流程为：采集一段语音信号。将语音信号的文件名命名为input18.wav，再用MATLAB中的wavread函数求出语音信号的三个参数，分别为：每个样本的值，生成该语音波形文件时的采样频率，波形文件样本的码数，再对信号及加入单频干扰后的语音信号做傅立叶变化，绘制出时域和频域的波形。最后通过滤波绘制滤波前后时域波形对比图和幅频特性对比图，并回放滤波前后的语音信号来验证是否达到去噪的目的。课程的设计流程图如图1-1所示：

图1-1设计流程图

2 设计原理

2.1 MATLAB简介

MATLAB是一个为科学和工程计算专门设计的交互式大型软件，是一个可以完成各种精确计算和数据处理的，可视化的，强大的计算工具。它具有丰富的函数资源和工具箱资源，语言精练，代码灵活，面向对象，控制功能优良，图形工能也强大。并且它的兼容性很好，几乎能在所有的PC机和大型计算机上运行，适用于Windows，UNIX和多种系统平台。MATLAB形形色色的工具箱中包括控制系统，信号处理，小波分析，统计，优化等，能够很好的运用于语音信号的滤波去噪。

2.2 滤波器

数字滤波器在数字信号处理的各种应用中发挥着十分重要的作用。它是通过对采样数据信号进行数学运算处理来达到滤波的目的。FIR数字滤波器设计的方法有三类，一类是窗口设计法（时间窗口法），第二类是频率采样法，第三类是等波纹优化设计。时间窗口设计法是从单位脉冲响应序列着手，使h(n)逼近理想的单位脉冲响应序列hd(n)；频率采样法是使所设计的FIR数字滤波器的频率特性某些离散频率点上的值准确地等于所需滤波器在这些频率点处的值，在其它频率处的特性则有较好的逼近。等波纹优化设计也叫最佳一致逼近准则，最佳一致逼近即选择N个频率采样值（或时域h(n) 值），在给定频带范围内使频响的最大逼近误差达到最小。可保证局部频率点的性能也是最优的，误差分布均匀，相同指标下，可用最少的阶数达到最佳化。本次课程设计采用的就是窗口设计法。

3 设计与实现过程

3.1实现方法

3.1.1 FIR滤波器

数字滤波器(Digital Filter，简称为DF)是指用来对输入信号进行滤波的硬件和软件。 所谓数字滤波器，是指输入、输出均为数字信号，通过一定运算关系改变输入信号所含频率成分的器件。数字滤波器和模拟滤波器相比，因为信号的形式和实现滤波的方法不同，数字滤波器具有比模拟滤波器精度高、稳定、体积小、重量轻、灵活、不要求阻抗匹配等优点。一般用两种方法来实现数字滤波器:一是采用通用计算机，把滤波器所要完成的运算编成程序通过计算机来执行，也就是采用计算机软件来实现;二是采用实际专用的数字处理硬件。

数字滤波器按照冲激响应的时域特性可分为:无限长单位冲响应滤波器（IIR）和有限长单位冲击响应滤波器（FIR），但与IIR相比，在满足同样阻带衰减的情况下需要的阶数较高，滤波器的阶数越高，占用的运算时间就越多，因此在满足指标要求的情况下应尽量减少滤波器的阶数。

FIR滤波器的基本结构可以理解为一个分节的延时线，把每一节的输出加权累加，可得到滤波器的输出，FIR滤波器的冲激响应h(n)是有限长的，数学M阶FIR滤波器可以表示为：

3.1.2窗口设计法

窗口设计法的基本思想是要选取某一种合适的理想频率选择性滤波器（这种滤波器总是有一个非因果，无限长的脉冲响应），然后将它的脉冲响应截断（或加窗）以得到一个线性相位和因果的FIR滤波器。

3.1.3凯塞窗

窗函数的主瓣宽度和旁瓣峰值衰耗是矛盾的，一项指标的提高总是以另一项指标的下降为代价，窗口选择实际上是对两项指标作权衡。而两项指标是跳变的，于是有人提出可调整窗，适当修改参数，可在这两项指标间作连续的选择。常用的可调整窗是凯塞（Kaiser）窗。凯塞（Kaiser）窗全面地反映主瓣与旁瓣衰减之间的交换关系， 可以在它们两者之间自由地选择它们的比重。

凯塞窗的表达式是：

3.2 设计过程

3.2.1录制语音信号

用windows工具中的录音机录制一段语音信号，语音为“请鞭挞我吧，公瑾！”，时间长度约为2s。将语音信号的文件名设置为input18.wav，并将文件保存在MATLAB下的WOK文件夹里面。然后在MATLAB平台上，用wavread函数调出此语音信号，并得到其采样率fs和比特数bits。

[x,fs,bits]=wavread('input18.wav') ; % 输入参数为文件的全路径和文件名，输出的第一个参数是信号的样本值，fs是生成该波形文件时的采样率，bits是波形文件每样本的编码位数。

sound(x,fs,bits); % 按指定的采样率和每样本编码位数回放录音

x=x(:,2);

N=length(x); % 计算信号x的长度

fn=1000; % 单频噪声频率

t=0:1/fs:(N-1)/fs; % 计算时间范围，样本数除以采样频率

x=x';

y=x+0.1.*sin(fn*2*pi*t); %y为加入单频干扰信号后的语音

sound(y,fs,bits) ;

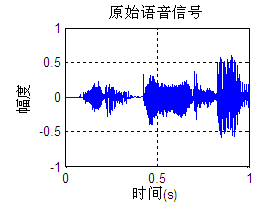
在MATLAB平台上，用plot函数画出原始语音信号，如图3-1所示：

图3-1

3.2.2 对原信号加入噪声

在MATLAB平台上，对原始信号和加噪信号进行fft变换,取幅度谱,并对频谱进行分析。具体实现如下：

[x,fs,bits]=wavread('input18.wav') ; % 输入参数为文件的全路径和文件名，输出的第一个参数是信号的样本值，fs是生成该波形文件时的采样率，bits是波形文件每样本的编码位数。

sound(x,fs,bits); % 按指定的采样率和每样本编码位数回放录音

x=x(:,2);

N=length(x); % 计算信号x的长度

fn=1000; % 单频噪声频率

t=0:1/fs:(N-1)/fs; % 计算时间范围，样本数除以采样频率

x=x';

y=x+0.1.*sin(fn*2*pi*t); %y为加入单频干扰信号后的语音

sound(y,fs,bits) ; % 对加噪信号进行回放

X=abs(fft(x));% 对原始信号进行fft变换,取幅度谱

Y=abs(fft(y)); % 对加噪后信号进行fft变换,取幅度谱

X=X(1:N/2); Y=Y(1:N/2); % 截取前半部分

f=0:deltaf:fs/2-deltaf; % 计算频谱频率范围

subplot(2,2,1);plot(t,x); axis([0 1 -1 1]); grid on; %画原始语音信号的时域图

xlabel('时间(s)');ylabel('幅度');title('原始语音信号');

subplot(2,2,2);plot(f,X);axis([0 4000 0 1500]); grid on; %画原始语音信号幅度谱图

xlabel('频率(Hz)');ylabel('幅度谱');title('语音信号幅度谱图');

subplot(2,2,3);plot(t,y); axis([0 1 -1 1]); grid on; %画加噪语音信号的时域图

xlabel('时间(s)');ylabel('幅度');title('加入单频干扰后的语音信号');

subplot(2,2,4);plot(f,Y);axis([0 4000 0 1500]); grid on; %画加噪语音信号幅度谱图

xlabel('频率(Hz)');ylabel('幅度谱');title('加入干扰后的语音信号幅度谱图');

在MATLAB上运行结果如图3-2所示：

由图3-2可以看出，对比原始信号与加噪信

号幅度谱图我们可以清晰的看到在1000Hz是出现了一个脉冲，从而使原有的音频听上去有了噪声，这样就到达了预期结果

3.2.2 滤波器的设计

滤波器设计就是要找到一组能满足特定滤波要求的系数向量a和b，而它主要是通过设计指标来实现的。滤波器设计的要求或指标一般是在频域上给出的，常用的滤波器频域指标有：fp1、fs1、fs2、fp2、Rp、As。要达到最佳的滤波效果，则需要对fp1、fs1、fs2、fp2和Rp、As进行适当的调整。由图3-3可以看出，语音信号可以选择fp1=900；fs1=950；fs2=1050；fp2=1100；Rp=1；As=60的滤波器。在MATLAB中，通常采用1/2采样频率进行归一化处理，如果将频率转化为角频率，则需将归一化频率乘以pi。设计程序如下：

fp1=900;fs1=950;fs2=1050;fp2=1100;Rp=1;As=60; % 带阻滤波器设计指标

fc1=(fp1+fs1)/2;fc2=(fp2+fs2)/2; df=min((fs1-fp1),(fp2-fs2)); % 计算上下边带中心频率，和频率间隔

wc1=fc1/fs*2*pi;wc2=fc2/fs*2*pi; dw=df/fs*2*pi; %将Hz为单位的模拟频率换算为rad为单位的数字频率

ws1=fs1/fs*2*pi;ws2=fs2/fs*2*pi;

M=ceil((As-7.95)/(2.285* dw)+1)+1; % 计算汉宁窗设计该滤波器时需要的阶数

n=0:M-1; beta=0.1102*(As-8.7); % 定义时间范围

w_kaiser= kaiser(M,beta); % 产生M阶的凯塞窗

hd_bs=ideal_lp(wc1,M)+ideal_lp(pi,M)-ideal_lp(wc2,M); % 调用自编函数计算理想带阻滤波器的脉冲响应

h_bs=w_kaiser'.*hd_bs; % 用窗口法计算实际滤波器脉冲响应

[db,mag,pha,grd,w]=freqz_m(h_bs,1); % 调用自编函数计算滤波器的频率特性

Rp=-min(db(wc1/dw+1:1:wc2/dw)); As=max(-round(db(ws2/dw+1:1:501)));

subplot(2,2,1);plot(w/pi,db);axis([0 0.2 -70 10]);

xlabel('w/pi');ylabel('dB');title('滤波器幅度响应图');grid on;

subplot(2,2,2);plot(w/pi,mag);axis([0 0.2 0 1.2]);

xlabel('w/pi');ylabel('幅度mag');title('滤波器幅度响应图');grid on;

subplot(2,2,3);plot(w/pi,pha);axis([0 1 -3 3]);

xlabel('w/pi');ylabel('相位pha');title('滤波器相位响应图');grid on;

subplot(2,2,4);stem(n,h_bs);axis([0 1500 0 1]);

xlabel('n');ylabel('h(n)');title('滤波器脉冲响应图');grid on;

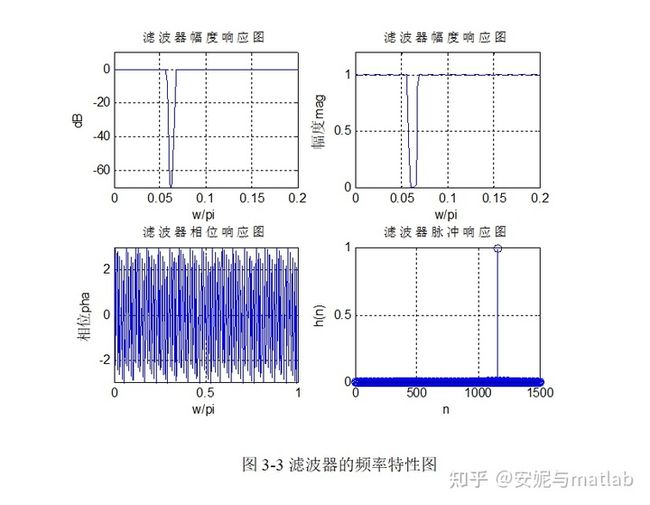
所设计的滤波器的幅度响应和脉冲响应如图3-3所示：

由3-3图可以看出Rp接近于0，而As大于开始的设定值（As=60db)，由此可见满足了设计要求，达到了设计目的。

3.2.2信号的滤波处理

滤波器设计完成后，在MATLAB平台上调用函数fftfilt对信号实现滤波，绘制语音信号去噪前后时域图，频域幅度图形并进行比较。具体程序如下：

y_fil=fftfilt (h_bs, y); % 用设计好的滤波器对y进行滤波

Y_fil=fft(y_fil);Y_fil=Y_fil(1:N/2); % 计算频谱取前一半

subplot(3,2,1);plot(t,x); axis([0 3 -0.2 0.2]);

xlabel('时间(s)');ylabel('幅度');title('原始语音信号x');grid on;

subplot(3,2,2);plot(f,X);axis([0 4000 0 70]);

xlabel('频率(Hz)');ylabel('幅度谱');title('语音信号幅度谱X');grid on;

subplot(3,2,3);plot(t,y); axis([0 3 -0.2 0.2]);

xlabel('时间(s)');ylabel('幅度');title('加干扰后的语音信号x1');grid on;

subplot(3,2,4);plot(f,Y);axis([0 4000 0 70]);

xlabel('频率(Hz)');ylabel('幅度谱');title('加干扰语音信号幅度谱X1');grid on;

subplot(3,2,5);plot(t,y_fil);axis([0 3 -0.2 0.2])

xlabel('时间(s)');ylabel('幅度');title('滤波后语音信号y');grid on;

subplot(3,2,6);plot(f,Y_fil); axis([0 4000 0 70])

xlabel('频率(Hz)');ylabel('幅度谱');title('滤波后语音信号幅度谱Y');grid on;

sound (y_fil,fs,bits)

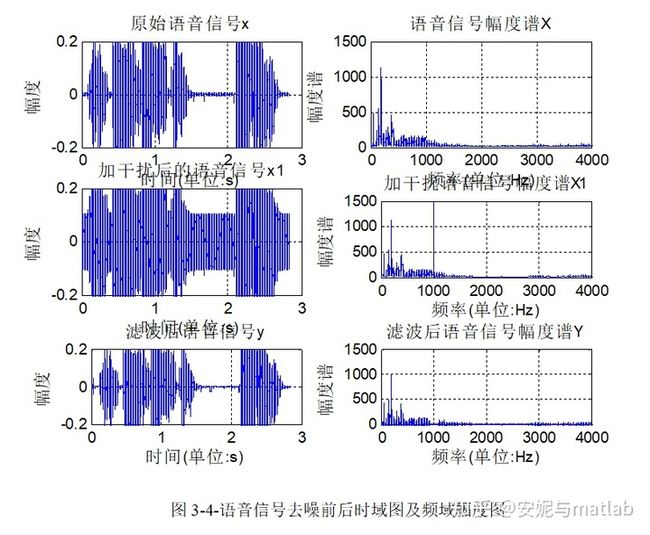
在MATLAB平台上的运行结果如图3-4所示：

由图3-4可以看出，在原始信号上加入的1000Hz 的脉冲信号已经被设计的滤波器滤去，符合实验所要到达的预期效果。

3.3 仿真结果与分析

通过观察滤波前后语音信号波形的变化，即观察图3-3，我们可以知道，原信号的时域图与滤波去噪信号的时域图基本相似；原信号与滤波去噪信号的频谱图波形也大致相似。通过观察可以看到，加噪信号的时域图中大部分都被加入的噪声给遮盖了，加噪信号的频谱图中，我们可以很明显地看到与原信号频谱图相比，它在频率1000Hz的地 方有一个尖脉冲，而滤波去噪信号的频谱图中该尖脉冲已经消失，幅度变为了零，波形大致与原图相似，可见滤波去噪效果基本不错。在将三个信号的时域波形和频谱图比较之后，我们还要通过回放去滤波去噪音乐信号，来跟原信号相比，以检验滤波器的效果。在MATLAB中，函数sound可以对声音进行回放。其调用格式为：sound (x，fs，bits)。用sound(y_fil,fs,bits)语句回放该滤波去噪信号，便可以感觉到滤波后的语音号与原信号差不多。

附录

附录1. 滤波器脉冲响应源程序

function [db,mag,pha,grd,w] = freqz_m(b,a);

% freqz 子程序的改进版本

% ------------------------------------

% [db,mag,pha,grd,w] = freqz_m(b,a);

% db = [0 到pi弧度]区间内的相对振幅(db)

% mag = [0 到pi弧度]区间内的绝对振幅

% pha = [0 到pi弧度]区间内的相位响应

% grd = [0 到pi弧度]区间内的群迟延

% w = [0 到pi弧度]区间内501个频率样本向量

% b = Ha(z)的分子多项式系数(对FIR b=h)

% a = Ha(z)的分母多项式系数(对FIR: a=[1])

%

[H,w] = freqz(b,a,1000,'whole');

H = (H(1:1:501))'; w = (w(1:1:501))';

mag = abs(H);

db = 20*log10((mag+eps)/max(mag));

pha = angle(H);

% pha = unwrap(angle(H));

grd = grpdelay(b,a,w);

% grd = diff(pha);

% grd = [grd(1) grd];

% grd = [0 grd(1:1:500); grd; grd(2:1:501) 0];

% grd = median(grd)*500/pi;

附录2. 理想低通滤波器计算源程序

function hd = ideal_lp(wc,M);

% 理想低通滤波器计算

% --------------------------------

% [hd] = ideal_lp(wc,M)

% hd = 0 to M-1之间的理想脉冲响应

% wc = 截止频率(弧度)

% M = 理想滤波器的长度

%

alpha = (M-1)/2;

n = [0:1:(M-1)];

m = n - alpha + eps;

hd = sin(wc*m) ./ (pi*m);