RSA加密算法Python实现
RSA加密算法Python实现
- 1.RSA算法简介
- 2.RSA算法涉及的数学知识
-
-
- 2.1互素
- 2.2 欧拉定理
- 2.3求模逆元
- 2.4 取模运算
- 2.5 最大公因数
- 2.6 最小公倍数
- 2.7 欧几里得算法
- 2.8 扩展欧几里得算法
-
- 3.RSA算法数学实现
-
-
- 3.1理论
- 3.2实践
-
- 4.RSA算法代码实现
-
-
- 4.1RSA算法代码实现1
- 4.1RSA算法代码实现2
-
1.RSA算法简介
1977年,三位数学家 Rivest、Shamir 和 Adleman 设计了一种算法,可以实现非对称加密。这种算法用他们三个人的名字命名,叫做RSA算法.RSA算法的特征如下:
- RSA算法是非对称加密算法,及算法的加密密钥与解密密钥不同
- RAS是基于大数分解问题实现的算法,
- RSA算法的密钥长度一般为1024位到2048位之间,密钥很长,加密较慢
- RSA算法一般用在数字签名比较多
- RSA还是分组密码算法,需要对明文进行一组一组加密
2.RSA算法涉及的数学知识
2.1互素
两个正整数,除了1之外没有其他公因子,我们称这两个数是互素的,(就是两个数除一外没有公约数,就是互素),如下是判断两个数是否互素的代码实现:
def prime(a, b):
if a > b:
mid = a
a = b
b = mid
mid = b % a
while mid:
b = a
a = mid
mid = b % a
if a == 1:
print('俩数互素')
else:
print('俩数不互素')
if __name__ == '__main__':
prime(8, 3)
2.2 欧拉定理
如果两个正整数a和n互素,则n的欧拉函数φ(n)可以让下面的式子成立
其中a上面的表达式为欧拉函数,欧拉函数的计算方法为,比如计算n的欧拉函数,就是找从1到n-1和n互素元素的个数,其中质数的欧拉函数值为n-1,判断一个数的欧拉函数值方法如下:
def prime(a, b):
if a > b:
mid = a
a = b
b = mid
mid = b % a
while mid:
b = a
a = mid
mid = b % a
if a == 1:
return True
else:
return False
def oula(n):
total = 0
for i in range(1, n):
if prime(i, n):
total = total + 1
return total
if __name__ == '__main__':
print(oula(8))
2.3求模逆元
求模逆元就是贝祖等式,就是d*e = 1 (mod n),e,和 n知道了,求d
def invmod(e, m):
"""
求模逆元:知道x * e + y * m = g
:param e:
:param m:
:return:
"""
g, d, y = exgcd(e, m)
assert g == 1
if d < 0:
d += m
return d
2.4 取模运算
取模运算就是取余数运算
model = a % b
2.5 最大公因数
求最大公因数一般使用欧几里得算法,
欧几里得算法又称辗转相除法,是指用于计算两个非负整数a,b的最大公约数。应用领域有数学和计算机两个方面。计算公式gcd(a,b) = gcd(b,a mod b)。
- 方法1
def gcd(a, b):
"""
求最大公约数
:param a:
:param b:
:return:
"""
if a > b:
mid = a
a = b
b = mid
y = b % a
while y:
b = a
a = y
y = b % a
return b
- 方法二
def gcd(a, b):
"""
求最大公约数
:param a:
:param b:
:return:
"""
while b:
a, b = b, a % b
return a
2.6 最小公倍数
最小公倍数是再最大公因数的基础上使用的,
两个或多个整数公有的倍数叫做它们的公倍数,其中除0以外最小的一个公倍数就叫做这几个整数的最小公倍数。整数a,b的最小公倍数记为[a,b],同样的,a,b,c的最小公倍数记为[a,b,c],多个整数的最小公倍数也有同样的记号。 与最小公倍数相对应的概念是最大公约数,a,b的最大公约数记为(a,b)。关于最小公倍数与最大公约数,我们有这样的定理:(a,b)x[a,b]=ab(a,b均为整数)。
- 方法1
def lcm(a, b):
"""
求最大公倍数
:param a:
:param b:
:return:
"""
divisor = gcd(a, b)
multiple = (a * b) / divisor
return multiple
- 方法二
def lcm(a, b):
"""
求最大公倍数
:param a:
:param b:
:return:
"""
return a // gcd(a, b) * b
2.7 欧几里得算法
欧几里得算法又称辗转相除法,是指用于计算两个非负整数a,b的最大公约数。应用领域有数学和计算机两个方面。计算公式gcd(a,b) = gcd(b,a mod b)。,上面说了
2.8 扩展欧几里得算法
求的a和b的最大公因数,求,x,y使得
x * a + y * b= g(a,b)
def exgcd(a, b):
# a:a和b的最大公因数
old_s:
old_t:
old_s * a + old_t * b = a
"""
old_s, s = 1, 0
old_t, t = 0, 1
while b:
q = a // b
s, old_s = old_s - q * s, s
t, old_t = old_t - q * t, t
a, b = b, a % b
return a, old_s, old_t
3.RSA算法数学实现
3.1理论
- 随意选择两个大的质数p和q,p不等于q,计算N = pq.
- 根据欧拉函数,求得φ(N)=φ§φ(q)=(p-1)(q-1)。这是一个公式
如果N = pq,那么φ(N)=φ(p)φ(q),又因为p和q都是素数,φ(p) = p-1,所以φ(N)=φ(p)φ(q)=(p-1)(q-1) - 选择一个数e,使e大于1,并且e小于φ(N),找一个数d,使得ed≡1(mod φ(N)),(e,n)为公钥,(d,e)为私钥
- 加密:m^e ≡ c (mod n),其中c为密文,解密:c^d ≡ m (mod n)
加解密图解如下:
3.2实践
首先找两个数,及p和q,p和q一般非常大,这里方便计算,取比较小的值,假设:p = 17,q = 19(p,q互素)
- n = p * q = 323
- φ(n) = (p-1) * (q-1) = 144
- 随机取一数e,使1 < e < φ(n)并且gcd(e,φ(n)) =1,e=5合适(还有很多数都合适,这里只取一个数)
- 取一数d,使得ed≡1(mod φ(n)),取d为29,所以公钥为(e,n),私钥为(d,n)
- 加密:假设明文 = 123,则 密文=(123的5次方)mod 323=225
- 解密:明文=(225的29次方)mod 323 =123,所以解密后的明文为123。
4.RSA算法代码实现
4.1RSA算法代码实现1
# 求两个数字的最大公约数(欧几里得算法)
def gcd(a, b):
if b == 0:
return a
else:
return gcd(b, a % b)
# 获取密钥
def get_key(p, q):
n = p * q
fyn = (p - 1) * (q - 1)
e = 2
while gcd(e, fyn) != 1:
e = e + 1
d = 2
while (e*d) % fyn != 1:
d = d + 1
return (n, e), (n, d)
# 加密
def encryption(x, pubkey):
n = pubkey[0]
e = pubkey[1]
y = x ** e % n # 加密
return y
# 解密
def decryption(y, prikey):
n = prikey[0]
d = prikey[1]
x = y ** d % n # 解密
return x
if __name__ == '__main__':
p = int(input("请给定第一个质数p的值:"))
q = int(input("请给定第二个质数q的值:"))
x = int(input("请给定要加密的消息x的值:"))
# 生成公钥私钥
pubkey, prikey = get_key(p, q)
print("加密前的消息是:", x)
y = encryption(x, pubkey)
print("加密后的消息是:", y)
after_x = decryption(y, prikey)
print("解密后的消息是:", after_x)
以上算法只能够实现整数加密,这个算法就是演示了RSA算法的原理
4.1RSA算法代码实现2
from random import randrange
import math
def prime(n):
"""
判断一个数是不是素数
:param n:
:return: BOOL
"""
mid = math.sqrt(n)
mid = math.floor(mid)
for item in range(2, mid):
if n % item == 0:
return False
return True
def generate_n_bit_odd(n: int):
"""
生成大数,不确定是不是素数
:param n:
:return:大数
"""
assert n > 1
return randrange(2 ** (n - 1) + 1, 2 ** n, 2)
first_50_primes = [3, 5, 7, 11, 13, 17, 19, 23, 29, 31,
37, 41, 43, 47, 53, 59, 61, 67, 71, 73,
79, 83, 89, 97, 101, 103, 107, 109, 113, 127,
131, 137, 139, 149, 151, 157, 163, 167, 173, 179,
181, 191, 193, 197, 199, 211, 223, 227, 229, 233]
def get_lowlevel_prime(n):
"""
选择满足不能够整除前50个素数的大数,没找到就一直循环
:param n:
:return:
"""
while True:
c = generate_n_bit_odd(n)
for divisor in first_50_primes:
if c % divisor == 0 and divisor ** 2 <= c:
break
return c
def miller_rabin_primality_check(n, k=20):
"""
米勒-拉宾素性检验
由于假设n是一个素数,n-1=a^s*d,s和d是常量,改变a的值,检测20次
:param n:
:param k:
:return:
"""
assert n > 3
if n % 2 == 0:
return False
# 找出n-1 = 2^s*d
s, d = 0, n - 1
while d % 2 == 0:
d >>= 1
s += 1
for _ in range(k):
a = randrange(2, n - 1)
x = pow(a, d, n)
if x == 1 or x == n - 1:
continue
for _ in range(s):
x = pow(x, 2, n)
if x == n - 1:
break
else:
return False
return True
def get_random_prime(num_bits):
"""
获取大素数
:param num_bits:
:return:
"""
while True:
pp = get_lowlevel_prime(num_bits)
if miller_rabin_primality_check(pp):
return pp
def gcd(a, b):
"""
求最大公约数
:param a:
:param b:
:return:
"""
while b:
a, b = b, a % b
return a
def lcm(a, b):
"""
求最大公倍数
:param a:
:param b:
:return:
"""
# divisor = gcd(a, b)
# multiple = (a * b) / divisor
# return multiple
return a // gcd(a, b) * b
def exgcd(a, b):
"""
扩展欧几里得算法
:param a:
:param b:
:return:
a:a和b的最大公因数
old_s:
old_t:
old_s * a + old_t * b = a
"""
old_s, s = 1, 0
old_t, t = 0, 1
while b:
q = a // b
s, old_s = old_s - q * s, s
t, old_t = old_t - q * t, t
a, b = b, a % b
return a, old_s, old_t
def invmod(e, m):
"""
求模逆元:知道x * e + y * m = g
:param e:
:param m:
:return:
"""
g, d, y = exgcd(e, m)
assert g == 1
if d < 0:
d += m
return d
def uint_from_bytes(xbytes: bytes) -> int:
"""
比特转换位整数
:param xbytes:
:return:
"""
return int.from_bytes(xbytes, 'big')
def uint_to_bytes(x: int) -> bytes:
"""
整数转换成比特的时候,一个整数对应32位比特数
:param x:
:return:
"""
if x == 0:
return bytes(1)
return x.to_bytes((x.bit_length() + 7) // 8, 'big') #做到尽量不补零
RSA_DEFAULT_EXPONENT = 65537
RSA_DEFAULT_MODULUS_LEN = 2048
class RSA:
"""
RSA算法(self.n, self.e)加密密钥
(self.n, self.d)解密密钥
"""
def __init__(self, key_length=RSA_DEFAULT_MODULUS_LEN,
exponent=RSA_DEFAULT_EXPONENT):
self.e = exponent
t = 0
p = q = 2
# 找出一个e使1
while gcd(self.e, t) != 1:
p = get_random_prime(key_length // 2)
q = get_random_prime(key_length // 2)
t = lcm(p - 1, q - 1)
self.n = p * q
self.d = invmod(self.e, t)
# 加密和解密使比特和整数之间的加解密
def encrypt(self, binary_data: bytes):
int_data = uint_from_bytes(binary_data)
return pow(int_data, self.e, self.n)
def decrypt(self, encrypted_int_data: int):
int_data = pow(encrypted_int_data, self.d, self.n)
return uint_to_bytes(int_data)
if __name__ == '__main__':
alice = RSA(512, 3)
msg = b'Textbook RSA in Python'
ctxt = alice.encrypt(msg)
m = alice.decrypt(ctxt)
print(m)
print(ctxt)
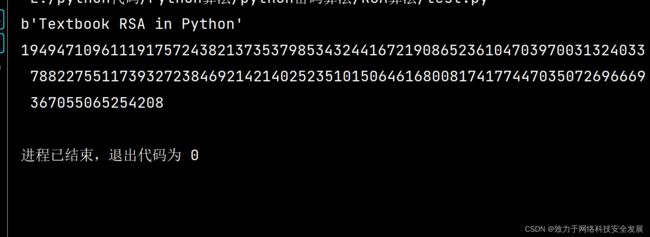
如下是结果运行图: