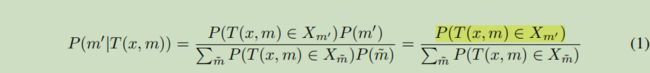异常检测(Out-of-distribution detection\ anomaly detection)相关论文阅读

Learning Confidence for Out-of-Distribution detection in Neural Network

作者 Terrance DeVries 、Graham W. Taylor
论文原地址：https://arxiv.org/abs/1802.04865

OOD : where a network must determine whether or not an input is outside of the set on which it is expected to safely perform

提到任何事物都有认知局限性，认识到这种局限性才可以最小化潜在风险

proposed：

1 train NN classifiers to output confidence estimates for input, and differeniate the in and out-of distribution examples.

2 misclassified in-distribution examples can be used as a proxy when calibrating ood detectors

motivation:

​以学生回答问题作为motivation。当学生回答问题时，对于不太确定的问题，可以申请hints，但是会受到penalty。对于high confidence的问题，不需要hints，对于low confidence的问题，需要hints，当所有问题回答完之后，根据一共申请了多少hints（或者是受到多生penalty），确定这个模型的置信度程度

model：

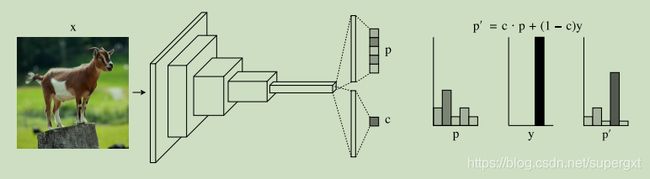
​ 在倒数第二层之后添加一个 confidence estimation branch，original模型有prediction branch and confidence branch.分别输出prediction probabilities p和confidence estimate c
$$p,c=f(x,\Theta )p_i,c\in [0,1],\sum _{i=1}^{M}pi=1.$$
上述motivation中提到的hints，通过interpolate between original predictions and target probability
$$p_i^{{}^{\prime }}=c\ast p_i+(1-c)\ast y_i$$
​ 这个式子还是蛮有意思的，通过置信度C，如果模型对该输入的预测置信度为1，则预测就是模型的预测，如果模型对该输入的预测置信度为零，就是模型完全不可信，则预测就是真实的标签，通过c的大小，来决定调整预测值有多少来自hints。

​ 像传统的softmax loss一样，不过是adjusted prediction propability. 但是只用这样的loss会有一个问题就是模型会把c学的特别低，这样输出都是真实的标签，loss也就越来越小，所以必须要对c有一个限制，添加一个log penalty，confidence loss
$$L_s=-\sum _{i=1}^{M}log(p_i^{{}^{\prime }})y_i$$
$$L_C=-log(c)$$
$$Loss=L_s+\lambda Lc$$

具体训练

三个关键点：

1 对于模型超参数lambda的选择

​ 在训练过程中，很容易所有的样本的c都会收敛到1，这样子就不会考虑hints了，也就和普通的softmax没有区别了，而理想应该是预测正确的样本 c -> 1,预测错误的样本 c-> 0.

​ 提出一个beta，作为预置参数，表示置信度惩罚项的最大值，具体实施:当Lc > beta, 就增加lambda，将Lc降下来；当Lc < beta，就减小lambda，总之就是让Lc维持在一个目标beta附近。

2 避免过度正则化

​ confidence learning可以看作一个很强的正则化，这在某些任务中可以看作是很强的抗过拟合方法，但是也有风险导致欠拟合（就是模型不去学复杂的decision boundry），因此该模型选择每个batch中一半的数据用之前的loss，另一半的数据还是只用传统softmax（也就是只有部分数据可以得到hints）

3 保留错误分类的training example

​ 当多参数模型遇到小量数据集时，会将训练集过拟合，也就是在训练过程中所有样本都被判断正确，但是在该模型中，判断错误的样本同样重要，因为他们会很大程度影响c。因此在训练过程中用了一些数据增强的方法。

一些操作

1 数据预处理

​作者希望数据在输入前就可以增加 in-distribution 和 out-distribution之间的差异性。论文中参考Fast Gradient Sign Method FGSM（GAN）通过对输入数据增加一些pertubation，使得模型更有几率进行错误分类。对图像进行干扰，使得模型能对in-distribution data输出更大置信度。

we observe that in-distribution examples increase in confidence more than out-of-distribution examples using this procedure, resulting in an easier separation of the two distributions

实验数据

in-distribution-dataset: SVHN, CIFAR-10

out-distribution-dataset: TinyImageNet, LSUN, iSUN, Uniform Noise, Gaussian Noise

---

---

Enhancing The Reliability of Out-of-distribution Image Detection in Neural Networks（2018 ICLR）

问题提出：

1 开篇同样是介绍OOD， However, when deploying neural networks in real-world
applications, there is often very little control over the testing data distribution. Recent works have shown that neural networks tend to make high confidence predictions even for completely unrecognizable or irrelevant inputs（对很能识别的或者完全无关的类输入也会产生高置信度。 这里给予的还是最基础的OOD方法，根据置信度判断）

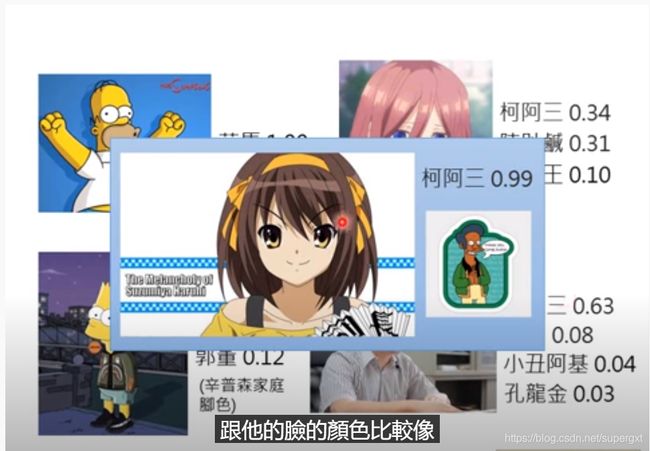
看到论文提到的这一点，联想到之前看李宏毅老师讲OOD的时候一个例子（不得不说李老师讲课真的好），他在做一个关于辛普森家族的分类任务时，输入一个其他动漫的角色，最大softmax输出达到了0.99，也就是模型对于这个样本的置信度很高，但其实这个数据应该是一个Out of distribution的，这就是上述提到问题的一个鲜明的例子。

2 2018年之前的工作training set都还需要包含一些ood data（很难获得），同时也提到如果想同时保证id data的效果和ood data的效果，那么需要一个大的网络框架。

方法基础：

1 论文“ A baseline for detecting misclassified and out-of-distribution examples in neural networks” 中提出 不需要重新训练模型，一个well-trained neural networks tends to assign higher softmax score to id examples

2 使用temperature scaling 和 small controlled perturbations可以提升id 和 ood之间的 softmax score gap

3 只需要用pretrain模型 + 上面两个手段就可以提升效果

方法核心：

1 temperature scaling

具体参考：

Calibration of Modern Neural Networks

首先学习一下temperature scaling的作用，在这之前需要了解一下knowledge distillation and calibrated（校准）。论文提出temperature scaling可以区分ID和OOD的最大softmax分数。那么什么是模型校准呢？

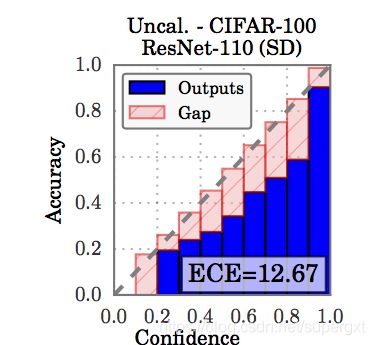
通常模型的输出是一个对应最大softmax的索引，也就是输出预测类，但是如果我们希望模型可以输出预测的置信度(confidence)是多少，那么这个confidence就是calibrated的。譬如：进行一个分类任务，将模型预测判断为某一类A且confidence score为90%的所有样本统计在一起，总数为N；并对着N个样本进行真实类别统计，如果有90%的样本都为A类，则说明该模型是calibrated的。

​ 如上图所示，横纵坐标分别是confidence和acc，蓝色图代表的模型输出，灰色线代表calibration。那么该模型就是较自信的（输出的confidence大于实际acc）譬如在confidence为0.8的这些输出中，期望的是有80%的应该分类正确，但实际只有60%分类正确，那么也就是“网络过于自信了”，输出的置信度具体式子如下：
$$\hat{y}=\frac{exp(z_i/T)}{\sum exp(z_j/T)}$$
如果没有参数T，那么置信度就是softmax对应最大值
$$\hat{y}=\frac{exp(z_i)}{\sum exp(z_j)}$$
T的作用可以这样理解：公式$T->\infty$ 时，$\hat{y}=\frac{1}{K}$ 其中K是类别数，也就时confidence score为1/K，那就是说模型完全的不确定是否判断正确（模型说”我是瞎猜的“），当$T->0$时，$\hat{y}=1$，也就是置信度为1(模型说”我预测的就是对的")，具体推导：

那么根据之前讲的 直接用argmax softmax作为置信度分数有些过于自信了，我们就可以设置参数T，调整他的置信度。注意的是，调整需要用valid set进行调整，训练后利用NLL调整参数T的值。

论文中是直接给定T，经过实验和推导证明T越大，检测效果越好

2 input preprocess

论文里提到对输入增加一个小扰动，其motivation是利用对抗样本，强迫模型输出错误的结果以及对应真实类别的低softmax score。但是论文里是相反的，希望利用一种扰动，使得输出的softmax score可以更高，the perturbation can have stronger effect on the in distribution images than that on out-of-distribution images, making them more separable。

实验

模型结构： DenseNet(Dense-BC), Wide ResNet

数据：训练集 CIFAR-10/ CIFAR-100 测试集 CIFAR-10/ CIFAR-100(ID) + TinyImageNet/LSUN/Uniform/Gaussian(OOD)

---

---

Unsupervised Anomaly Detection via Deep Metric Learning with End-to-End Optimization（2020）

proposed

1 无监督的异常检测（就是只有单标签正常训练数据）（标签信息难以获取，也有可能出现训练集没有出现过的异常类别，因此无监督的异常检测方法是更为合理的存在）

2 当前针对large-scale, high-dimension的数据往往都是两阶段的：先用降维方法投影到低维空间，再使用异常检测模型进行建模，问题是在第一步的时候其实并没有考虑“异常检测”这个任务，所以投影的空间一般是suboptimal的。

3 hard normal mining。我们知道DML中一个很好的trick是 hard negative mining 用来选择真正有效的负样本。本文参考了硬正常样本挖掘(Smart mining for deep metric learning CVPR 2017)，只对离数据中心点最远的数据进行学习。

4 论文证明了传统的contrastive loss如果只有一个类别的样本时，损失函数存在一个恒等式：
$$\begin{gathered} L_{contrastive}=\frac{1}{|M{|}^2}\sum _{i=1}^{|M|-1}\sum _{j=i+1}^{|M|}{\Vert f(x_i)-f(x_j)\Vert }_2^2 \\ =\frac{1}{|M|}\sum _{i=1}^{|M|}{\Vert f(x_i)-\mu \Vert }_2^2=L_{center} \end{gathered}$$
其中$ \mu $是所有数据的均值。也就是说当所有数据为一个类别时，对比损失函数转化为所有数据与均值点之间的距离。

5 anomaly scoring function的计算。 论文对异常样本的检测还是沿用传统的思路：提出一个anomaly score和threshold 如果score 大于 threshold 判断为异常样本，反之就为正常样本。论文先是说既然传统的损失函数计算的其实就是一个样本与所有其他样本的距离的均值的期望也就是最小化：
$$E_{X_t\in M}[\frac{1}{M}\sum _{x_j\in M}{\Vert f(x_t)-f(x_j)\Vert }_2^2]$$
那么自然就可以把待测样本与所有训练数据的距离均值作为anomaly score, 但是存在一个问题，这个计算复杂度是O(n)的，效率不高。根据第四点恒等式的存在，那么就可以通过构造待测样本与训练样本映射空间的均值的距离作为分数也就是
$$S(x_t)={\Vert f(x_t)-\mu \Vert }_2^2$$
因为$\mu$不变，所以计算起来只有O(1)的复杂度。

model

模型其实很简单，特征映射部分只用了简单的全连接层，论文的创新点全部集中后图的右半部分。体现如下：

1 前面提到的$L_{contrastive}$和$L_{center}$和设计的anomaly score $S_{center}$ 在图中有所体现。

2 图中的$\tau$，在下面会介绍，就是规定的训练数据的范围。

highlight

1 data distillation

论文提到在训练过程中，并不是所有的训练数据都是完全正常的（Anomaly detection methods often assume nearly all the training data as normal and provide good performance when the assumption holds and their performance significantly deteriorates if this assumption in wrong ）。所以作者采用在每个epoch开始之前，先把训练数据筛选一遍，譬如当前epoch模型参数为$f(.)$， 那么就用这个模型对所有训练数据求anomaly score，根据score选择训练集
$$\begin{gathered} P=\{x_i|{\Vert f(x_i)-\mu \Vert }_2<\tau \} \\ F=\{\Vert f(x_i)-\mu \Vert \}{x}_i\in M \\ \tau =max(SmallestK(F,K=\rho \ast |M|))\rho \in (0,1] \end{gathered}$$
P就是蒸馏出来的训练集子集，这一个epoch只用这些数据训练，\tau怎么确定呢，取前$M\ast \rho$ 个最小的F值对应的训练数据，这些最小的F值中最大的是$\tau$。也就是在这个epoch训练中，限制了一个region，只有这个region内的数据参与训练。

**论文进一步提到 这一个trick里面的超参数其实是$\rho$ ,而不是直接规定这个范围的大小。这样做的好处是增加可解释性以及不需要为每一个数据集特定选择$\tau$。**这一点倒是一个很好的点，因为在本人实际利用DML的时候，往往要尝试很多margin超参数。

2 minibatch

在利用 distillation之后，论文提到用mini-batch进行训练。这个没什么太多可解释的，论文里主要是介绍一下一个batch的loss怎么计算。

2 hard normal mining

硬挖掘是通过选择训练数据中那些对模型来说具有挑战性的数据进行学习，而不是去拟合所有的数据，因为很多数据模型学起来很简单，就会出现过拟合的现象。具体的挖掘过程如下：

(1) 所有训练数据经过蒸馏，获得一个子训练集

(2) 对子训练集进行mini batch构建

(3) 在每一个batch里面选择$\rho$个最难例样本，难例样本的判断还是根据之前计算的距离，距离越大，就越难。

---

---

2020 ICLR CLASSIFICATION-BASED ANOMALY DETECTION FOR GENERAL DATA

Motivation

1 论文提出当前无监督异常检测的方法可以分为三大方向：Reconstruction-based, Distribution-based 和 Classification-based，分别从重构误差、概率密度和one-class分类三个角度优化模型，并且提到三者的缺点分别是：

“Reconstruction-based 常用深度模型是GAN网络，而GAN网络容易模式崩溃，并且在2018 DAGMM中也提到，Reconstruction-based model往往存在一些重构误差很低的异常点”

“Distribution-based 模型提到概率模型往往基于一个较强的概率假设，当然公认比较好的DAGMM，在我个人实验的过程中，发现GMM的数量，以及模型的结构设计都是有一定难度的”

“Classification-based 模型从OC-SVM, SVDD 发展到 Deep SVDD，最大的问题就是因为只有单类，怎么从训练样本中提取具有高辨别性的特征是比较困难的问题，现在基于图像的异常检测往往可以通过自监督以及辅助任务进行改进，但是怎么运用到general data上是一个待解决的问题。”

2 论文主要参考了2018年NIPS的一篇利用几何变换进行anomaly detection的工作(Geometric-transformation classification GEOM)。利用几何变换包括(rotation, reflection, translation)等将训练集中的图片$x$映射到$T(x,1)...T(x,M)$其中M是变换的数量，利用变换后的数据可以构造一个分类模型，用来区分每个转换图像对应的转换类型，即标签m。最终模型预测条件概率：

假设原始数据数据分布所在区域为$X$ , 即$x\in X$, 经过几何变换后的区域为$X_m$ ，即$T(x_m) \in X_m $。则异常数据$X_a \in R - X$，在经过m变换后，图像应该不会落在$X_m$中，即 $ P(m|T(x_a, m)) $是一个很小的值。

GEOM模型利用测试集上
$$P(m|T(x,m))$$
作为异常分数。

Model

提出的GOAD方法结合了one-class的思想和transformation-based的思想。同样将$X$经过m个几何变换投影到不同的区域（同一维度下），通过训练一个neural network，将这些变换过后的数据映射到新的样本空间。在OC的思想下将每个几何变换子空间$X_M$映射到一个sphere中，中心是$c_m$. 则变化样本点属于某个变化的概率为
$$P(T(x,m)\in X_m^{\prime })=\frac{1}{z}{e}^{-(f(T(x,m)-c_m^{\prime }){)}^2}$$
则归一化后每一类的输出概率为
$$P(m^{\prime }|T(x,m))=\frac{e^{-||f(T(x,m))-c_{m^{\prime }}|{|}^2}}{\sum e^{-||f(T(x,m))-c_m|{|}^2}}$$
利用center triplet loss进行优化

公式表明希望 一个样本的m变化 $f(T(x_i,m))$ 与这种变化对应的中心之间的距离要小于该变化样本与其他所有变化对应中心的最小距离，并且之间的距离差要大于一个margin，通过这种方式将每个变化的样本压缩到一个很小的sphere中。

源码中loss是 Tripletcenterloss 和 softmaxloss的加权和

经过这样一个损失的优化之后，模型的后验概率应该有一个较好的表现，但是文章提到，当数据远离分布的时候(仍然是normal data)，距离会很大，”A small difference in distance will make the classifier unreasonably certain of a particular transformation” 。 这句话我的理解是：**当一个在原始分布就离分布中心较远的数据，在经过几何变换后，肯定也会离变换中心$c_m$ 较远， 则在这种情况，如果发生了一点小小的变化，分类器就会将模型分错了（本身样本点就在类别边界处，稍微有一个扰动，分类器就分类错了。 **因此就在分类模型上添加一个常数约束项
$$P(m^{\prime }|T(x,m))=\frac{e^{-||f(T(x,m))-c_{m^{\prime }}|{|}^2}+ϵ}{\sum e^{-||f(T(x,m))-c_m|{|}^2}+M\ast ϵ}$$
这个式子有什么用呢？可以简单设想一下：
$$\frac{a}{b}>\frac{a+ϵ}{b+Mϵ}$$
当 $aM>b$时，恒成立，结合原式，当判断真实类别概率时$P(m|T(x,m))$ ，因为对应概率最大（也就是$aM>b$恒成立了），所以就是把正确分类的概率减小一点。那么为什么要小一点呢？ 因为这个值越小，对应的的异常分数就越高。也就是希望判别模型可以把不太确定的样本认为是异常的。（提升异常样本召回率）最终确定了一个异常分数：
$$Score(x)=-log\prod P(m|T(x,m))=-\sum logP(m|T(x,m))$$
也就是每个变换对应正确类的概率密度对数和的负数，越大则约异常。

---

---

Deep One-Class Classfication(Deep-SVDD) 2018 ICML

参考链接：2018 ICML Deep One-Class Classfication(Deep-SVDD) 论文阅读&源码分析 (Anomaly Detection)

---

---

Explainable Deep One-Class Classfication 2021 ICLR

参考链接: 2021 ICLR Explainable Deep One-Class Classfication论文阅读总结

---

---

Memorizing Normality to Detect Anomaly: Memory-augmented Deep Autoencoder for Unsupervised 2019 ICCV

参考链接：2019 ICCV Memorizing Normality to Detect Anomaly: Memory-augmented Deep Autoencoder for Unsupervised论文阅读总结

Entropy Maximization and Meta Classification for Out-of-Distribution Detection in Semantic Segmentation 2021 ICCV

参考链接: Entropy Maximization and Meta Classification for Out-of-Distribution Detection in Semantic Segmentation