2020李宏毅机器学习学习笔记--1.概论与Regression回归
第一节课 课程介绍概论(P1)
一. 机器学习的本质就是自动寻找函式
比如:
------输入语音信号,输出文字信号
------输入图片,输出内容
------输入一个问题,输出一个答案
二. 机器学习包含以下
-1.—Regression(回归):
The output of the function is a scalar,函数的输出是一个数值
2.—Classification*(分类)
1).Binary Classification(二元分类): 输出只有两种可能,正面或负面
2).multi-class Classification(多层次分类) :输出当前输入属于既定N个类别的概率值,并将N个概率值中最大者所对应的类别作为正确答案。
3.—Generation(生成) 输出有结构的复杂东西。如翻译,画图,文句。
三. 怎么告诉机器我们要找什么样的函式?
监督学习(supervised learning)
给机器带有标签的数据让他训练分类器(函式)。
再用一个LOSS函数去判断这个分类器(函式)效果是否好。
让机器自动找出Loss最低的分类器。
强化学习(Reinforcement Learning)
强化学习与监督学习的区别
以下围棋为样例解释
监督学习需要和机器说,在这个局面中下一步需要怎么下;而强化学习不需要和机器说下一步,是让他和对手下棋,让他在赢局中思考自己下的好的地方,以及在输局中思考自己不足之处。如果机器完成的好就奖励,完成的不好就惩罚(奖励和惩罚是两种更新模型参数的式),最后机器学到的就是对于每一个步骤,应当如何处理才让得到好结果的概率最大。alphaGO是监督学习与强化学习结合的产物,其升级版alphaGO zero是完全的强化学习的产物。
非监督学习(Unsupervised Learning)
拥有大量数据,但是没有先验知识无法标注或者很难标注,但是又希望得到其中数据的结构时,就涉及无监督学习。无监督学习的典型例子就是聚类。
机器怎么找出我们想要的函式
目前的机器学习,不是要求机器凭空的产生一个较优的函数,而是给机器一个函数结构(特定函数集合),让其去学出一组较优参数。然后机器通过这组参数所决定的函数,就可以较好的完成给定任务。线性函数、CNN和RNN,svm等都是函数结构,函数结构决定了机器所能的搜寻的函数的范围。
使用方法寻找函式
梯度下降(Gradient Descent)(后面视频中详细理解)
获取最佳函数典型方法-梯度下降(gradient decent)
梯度下降(GD)是将风险函数、损失函数最小化的一种常用的方法,是神经网络模型训练最常用的优化算法。对于深度学习模型,基本都是采用梯度下降算法来进行优化训练的。
前沿研究
1.Explainable AI 告诉我们判断/分类等原因
2.Adversarial Attack 用神奇的杂序攻击分类器,
3.Network Compression 把网络缩小放到手机等设备上
4.Anomaly Detection(异常检测) 放一些不是预期的输入信息时,是否可以识别出来 即如何让机器知道他不知道
5.Transfer Learning(迁移学习)(Domain Adversarial Learning) 训练测试信息的分布不一样,类型不一样(比如用黑白手写数字照片训练,但用彩色手写数字照片测试)
6.Meta Learning(元学习) 让机器学习如何学习,自己发明学习算法,比我们设计的算法更有效
7.Life-long Learn 终身学习,不断学习
第二节 课程的要求(P2)
第三节 -Regression(P3)
认识–Regression能够做哪些事情?
- (股票行情预测)输入股票10年趋势,输出明天该股票的变化
- (自动驾驶)输入汽车周围的信息,输出汽车的运行策略
- (推荐系统)输入使用者和商品,输出使用者购买商品的可能性
Regression回归案例分析—宝可梦研究计划
预测宝可梦进化后的CP值
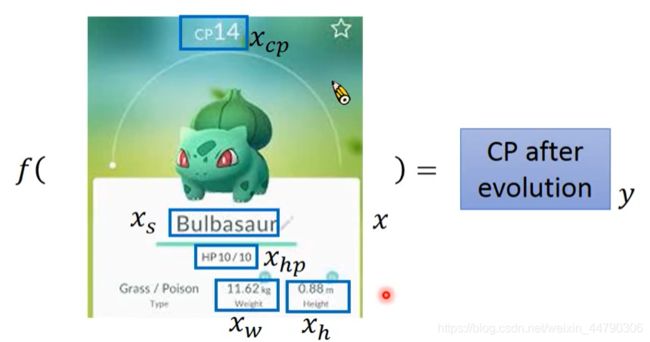
输入为某一只pokemom,输出为进化后的战斗值CP
X: 表示一只宝可梦,用下标表示该宝可梦的某种属性
X cp:表示该宝可梦进化前的cp值
X s: 表示该宝可梦是属于哪一种物种,比如妙瓜种子、皮卡丘
X hp:表示该宝可梦的hp值即生命值是多少
X w:表示该宝可梦的重量
X h:代表该宝可梦的高度
f(): 表示我们要找的function
y:表示function的output,即宝可梦进化后的cp值.
解决的思路
确定Senario(方案)、Task(任务)和Model(模型)
Senario
首先根据已有的data来确定Senario,我们拥有宝可梦进化前后cp值的这样一笔数据,input是进化前的宝可梦(包括它的各种属性),output是进化后的宝可梦的cp值;因此我们的data是labeled,使用的Senario是监督学习。
Task
根据我们想要function的输出类型来确定Task,我们预期得到的是宝可梦进化后的cp值,是一个scalar,因此使用的Task是Regression
Model 关于Model,选择很多,从简单的开始这里采用的是Llinear Model
机器学习的步骤
1.定义一个model即function set
2.定义一个goodness of function损失函数去评估该function的好坏
3.找一个 best function
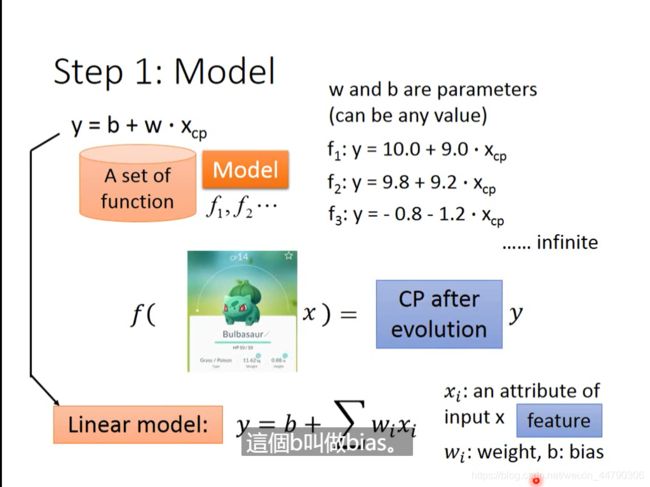
Step1:Model (function set)
y=b+w∗x cp
b、w为参数,参数不同,对应的模型函数就不同
Step 2: Goodness of Function
寻找合适的参数b和w,使得模型函数效果好
Loss function损失函数是函数的函数,用于衡量参数的好坏。
要选出唯一一个function,我们需要衡量一个function的好坏,称之为loss function(损失函数),之前提到的model是由我们自己决定的,这里的loss function也是,最常用的方法就是采用类似于方差和的形式来衡量参数的好坏,即预测值与真值差的平方和;这里真正的数值减估测数值的平方,叫做估测误差Estimation error,将10个估测误差合起来就是loss function
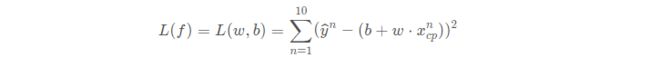
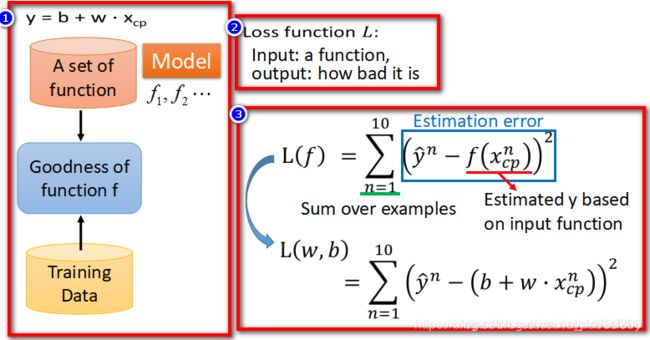
Step3: Best Function
已经确定了loss function,他可以衡量我们model里面每一个function的好坏,接下来我们要做的事情就是,从这个function set里面,挑选一个最好的function。挑选最好的function这一件事情,写成formulation/equation的样子如下:
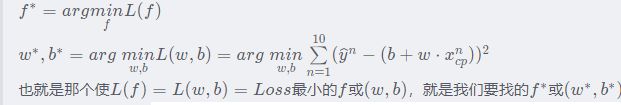
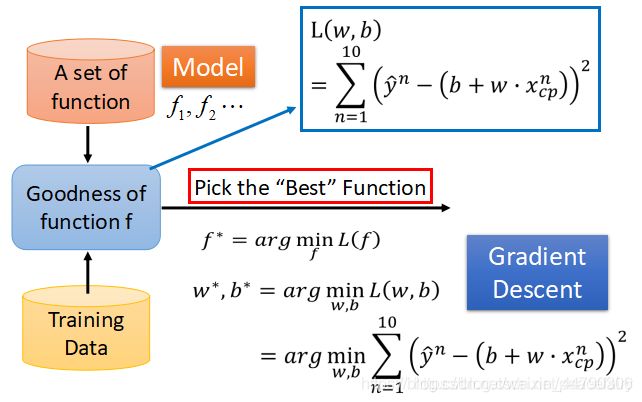
通常我们都采用Gradient Descent 来挑选出最好的function。
因为对于loss function的计算,我们穷举是不太现实的。所以我们采用的梯度下降方法来更新我们的参数来找到是loss最小的那套参数。
求解方法–梯度下降法
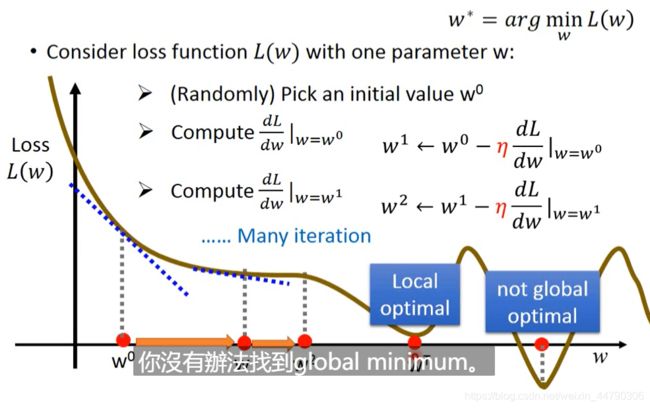
一.Loss function先讨论只有一个参数的情况
w *=argminL(w) 使得损失最小的参数w
步骤如下:
1.随机挑取一个初始点w0;
2.计算 d L d w ∣ w = w 0 \frac{dL }{d w }∣_{w = w ^0}\quad dwdL∣w=w0
如果导数为正,则需减小w;如果导数为负,则需增加w;使得值变小
3.改变w的时候走的步长,首先由微分值定,微分值越大,说明越陡峭,则走的就越多;同时,又由η (学习率)决定,它是提前确定好的,它若大,则走一步,数值更新的幅度就越大,学习的速度就越大。
4. w 1 = w 0 − η d L d w ∣ w = w 0 w1=w0-η\frac{dL }{d w }∣_{w = w ^0}\quad w1=w0−ηdwdL∣w=w0
5.更新w后,重新2、3、4直到微分=0,则找到值最小的点。
二.Loss Function是关于两个参数的函数
w*=argminL(w,b)使得损失函数最小的参数w, b
步骤如下:
1.随机选取一个初始点w0,b0;
2.计算 d L d w ∣ w = w 0 , b = b 0 \frac{dL}{dw}|_{w=w^0,b=b^0}\quad dwdL∣w=w0,b=b0
d L d b ∣ w = w 0 , b = b 0 \frac{dL}{db}|_{w=w^0,b=b^0}\quad dbdL∣w=w0,b=b0
如果导数为正,则需减小w,b;如果导数为负,则需增加w,b;使得Loss 变小
3.改变w,b的时候走的步长,首先由微分值定,微分值越大,说明越陡峭,则走的就越多;同时,又由η (学习率)决定,它是提前确定好的,它若大,则走一步,数值更新的幅度就越大,学习的速度就越大。
4. w 1 = w 0 − η d L d w ∣ w = w 0 , b = b 0 w1=w^0-η\frac{dL }{d w }∣_{w = w ^0,b=b^0}\quad w1=w0−ηdwdL∣w=w0,b=b0
b 1 = b 0 − η d L d b ∣ w = w 0 , b = b 0 b1=b^0-η\frac{dL }{d b }∣_{w = w ^0,b=b^0}\quad b1=b0−ηdbdL∣w=w0,b=b0
5.更新w,b后,重新2、3、4直到微分=0,则找到loss最小的点
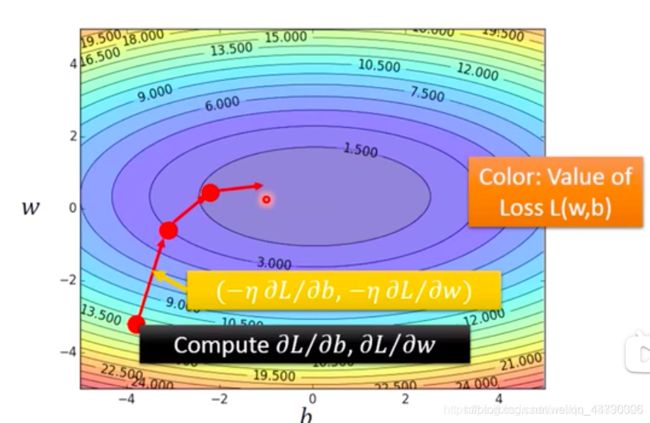
因为梯度下降法选取的初始点不同,最终找到的结果也不一定相同,可能是不同地方的局部最小值。但是,在线性函数中,没有局部最小值,找到的都是全局最小。
结果RESULT
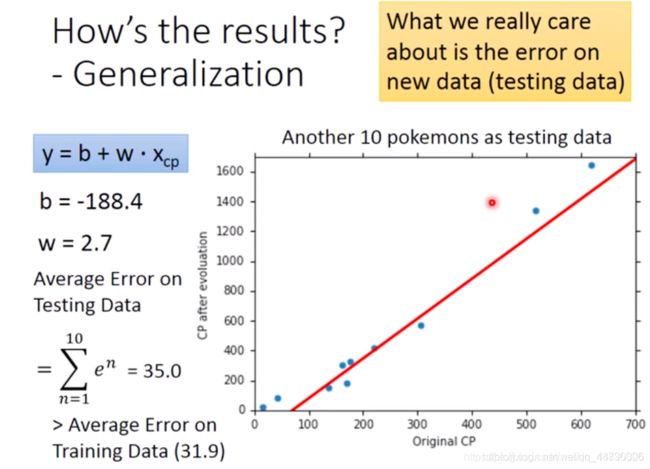
根据gradient descent,我们得到的 y = b + w ⋅ x c p y=b+w\cdot x_{cp} y=b+w⋅xcp中最好的参数是b=-188.4, w=2.7
我们需要有一套评估系统来评价我们得到的最后这个function和实际值的误差error的大小;这里我们将training data里每一只宝可梦 i 进化后的实际cp值与预测值之差的绝对值叫做 e i e^ i ei ,而这些误差之和Average Error on Training Data为 ∑ i = 1 10 e i = 31.9 \sum\limits_{i=1}^{10}e^i=31.9 i=1∑10ei=31.9
我们真正关心的是generalization的case,也就是用这个model去估测新抓到的pokemon,误差会有多少,这也就是所谓的testing data的误差;于是又抓了10只新的pokemon,算出来的Average Error on Testing Data为 ∑ i = 1 10 e i = 35.0 \sum\limits_{i=1}^{10}e^i=35.0 i=1∑10ei=35.0
可见training data里得到的误差一般是要比testing data要小,这也符合常识。
效果并不是很好。
我们猜测,更合适的模型function可能不是线性的。
Step4: Select another Model
y = b + w 1 ∗ ( x c p ) + w 2 ∗ ( x c p ) 2 y=b+w 1 ∗(x cp) +w 2 ∗(x cp) ^2 y=b+w1∗(xcp)+w2∗(xcp)2
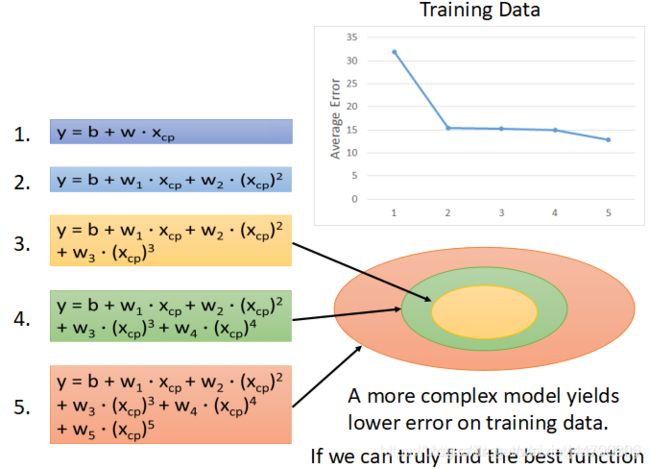
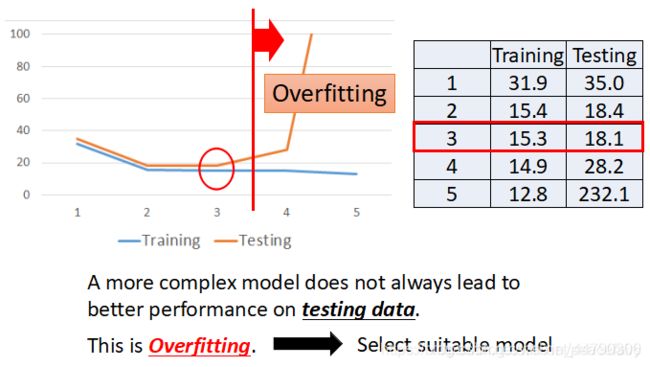
结果可见用越来越复杂的模型,训练误差会越来越小,但是测试误差会越来越大,这就出现了overfitting过拟合!因此我们得知model不是越复杂越好,而是选择一个最适合的model。
Step 5: Improve Model
之前model只考虑了宝可梦进化前的cp值,这显然是不对的,除了cp值外,还受到物种Xs的影响。
然后用60个数据做实验,发现还和物种有关。修改模型,每个物种对应一种参数w,b。
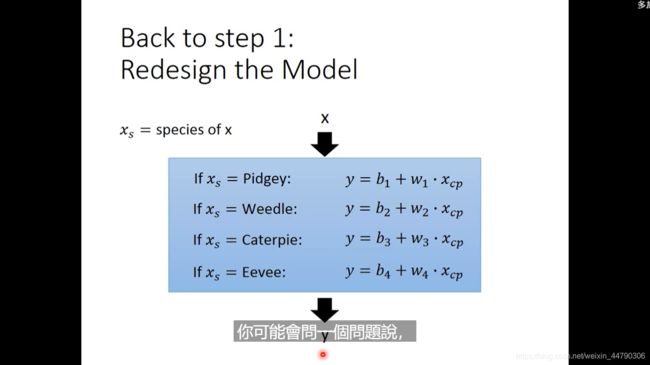
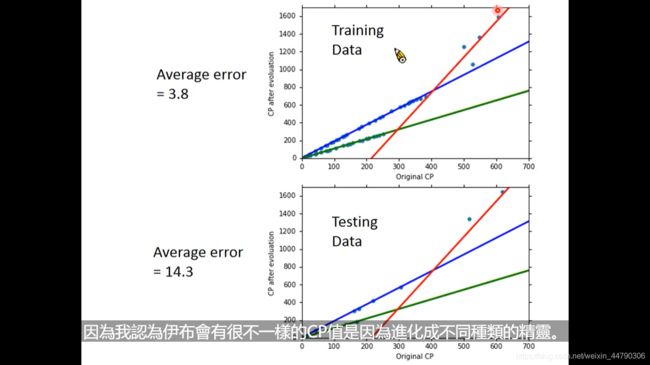
效果比之前更好了,但testing data 还是有些点稍微有点偏。可能还有些其他的因素影响,比如可能是high,weight,hp等。
针对过拟合问题的解决方案-Regularization(正则化)
改变Loss Function结构,通过增加一个regularization项,使得函数更加平滑,当测试数据时有杂讯干扰,对平滑函数会有更小的影响。
正则化的作用是降低模型的泛化误差(测试误差),其中λ是由我们自己进行设置的。

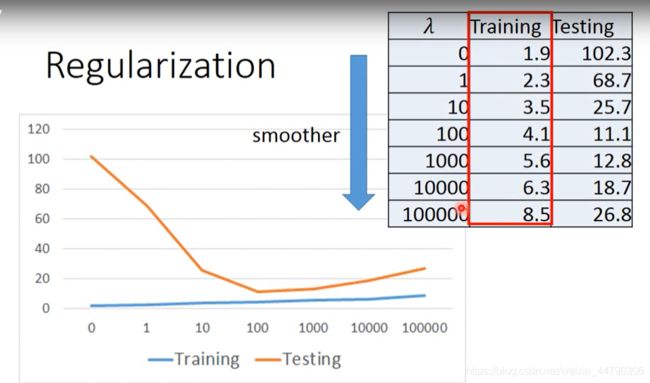
L2正则化就是在惩罚w,在Loss function 里加入正则项,最小化L的时候,既考虑error误差也考虑w,在减少errror误差的同时也让w减到很小。有较小的w的函数是比较平滑的,对于输入的变化不那么敏感。选择合适的λ,可以提升模型的泛化能力。(bias不参与正则化,因为它不影响函数的平滑度)