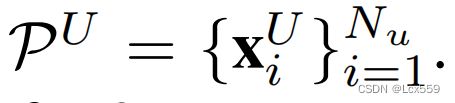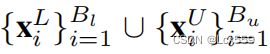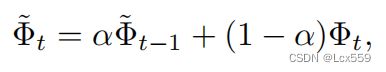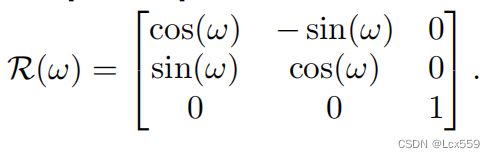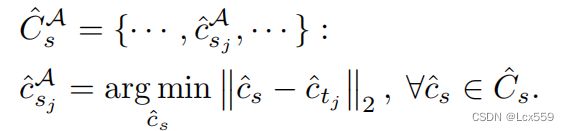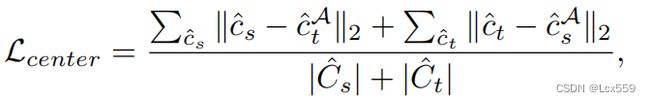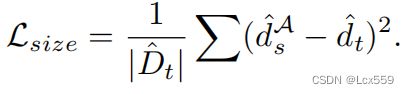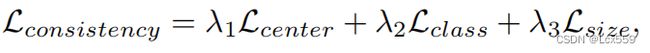SESS: Self-Ensembling Semi-Supervised 3D Object Detection论文阅读及理解

SESS: Self-Ensembling Semi-Supervised 3D Object Detection

Abstract

3d检测通常以来目标的标签和注释，然而获得这些注释是十分困难的。

SESS一种自集成的半监督三维目标检测框架。

设计了一种扰动方案，加强对未标记数据和新的为可见数据的泛化。

提出三种一致损失（consistency loss），加强两组预测三维目标提议之间的一致性。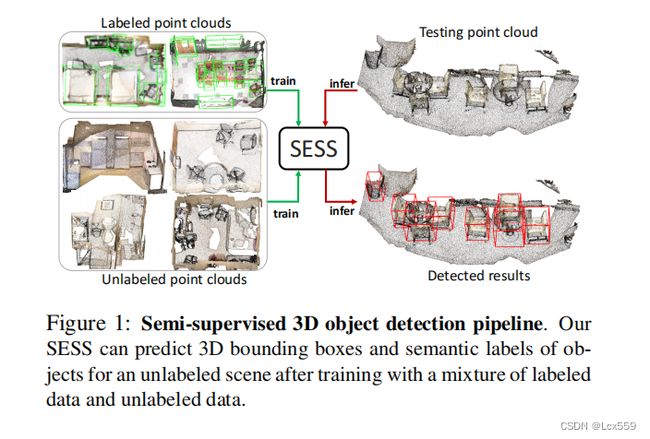

 半监督学习的方式，通过一个混合标签的数据和为标注的数据进行训练。

Introduction

半监督学习只需要很小一部分的标签，很大程度的减少了收集大量数据标签的问题。

3d目标检测任务中完全去除标签是不太可能的，因为3d点云的稀疏性和无序性，且物体容易被阻挡。

SESS通过包含了教师和学生网络的教师平均范式3d目标检测网络进行半监督学习。教师网络指导学说网络在面对不同的扰动下保持相同的预测。在训练结束时，我们希望能够让教师网络和学生网络提出的检测提案是一致的。

提出三种一致性损失，分别是提案的中心点、类别以及大小（bounding box）。

Our Method

Problem Definition

在半监督学习的设定中，输入为N个训练样本，其中包括了Nl个有标签的点云PL，

 和u个未标签的点云

 表示点云的表示场景，具有n个点的3为特征向量。

 以标签点云的真实标签（ground truth）。

 每个对象都由一个语义类s表示（占预定义类的1/1000）.

bbx由中心点坐标和他的大小和沿直立轴的转角θ表示表示。

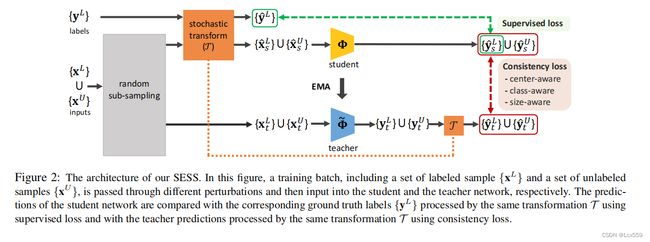
SESS Architecture

SESS总体架构如图：

 将两个有标签和无标签的点云作为输入

 Bl和Bu表示一次采样中标签和未标签样本。首先随机从点云中采样M个点，得到两个点集，将第一个点集Xs通过一个随机的变换矩阵T进行扰动，得到X^s，另一个点集Xt直接送至教师网络，得到的预测Yt也通过同样的随机变换矩阵进行扰动得到Y^t。

对于Y^t中的每个提案，通过欧几里得距离从学生网络预测的Y^s中找到最接近的提案。每个对齐的提案的误差由上述的三个一直损失计算得到。

同时XLs对应的ground truth YL经过同样的变换矩阵T，得到的变换矩阵Y^L于学生网络的输出Y^LS通过监督损失进行比较。

最后，学生网络的参数Φ通过梯度下降进行更新，而将学生网络的参数以指数平均的方式对教师网络的参数Φ~进行平均：

 α是一个超参数，控制教师网络从学生网络中获得多少信息。

Perturbation Scheme

数据扰动和数据扩张对于自集成方案有着很大的作用。

Random Sub-sampling

对学生网络和教师网络的部分都采用了随机子采样作为扰动方案。

Stochastic Transform

对学生网络子采样的点集进行翻转、缩放以及旋转。具体来说，将变换作设置为一个随机的变量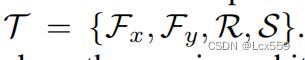：Fx表示沿x轴的随机翻转，Fy表示沿y轴的随机翻转，Fx的值取决于：

从[0，1]中随机取值，Fy的值类似获得。

R表示绕直立轴的旋转矩阵，w从[-θ，θ]中随机采样：

 S从[a，b]中均值采样用来表示缩放。

最终产生的矩阵Ti用于令输入学生网络的点云Xs进行变换，注意，ground truth label yLi在用于计算监督损失之前也需要通过相同的Ti矩阵进行变换。教师网络输出的预测yt也需要通过相同的矩阵进行变换。

 

Consistency Loss

两组三维对象提案的一致性是不能直接计算的。

将来自学生网络和教师网络的提案进行配对，然后使用三个一致性损失进行计算。

作为学生网络bounding box的预测中心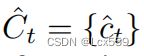，作为变换后的教师网络预测的中心。对于教师网络预测的每个中心点c^t和学生网络预测的中心点通过最小的欧氏距离进行对其。进一步使用表示学生网络预测的中心点和教师网络预测中心点对其的点，表示为：

 

同样收集教师网络与学生网络以欧氏距离判断的最接近的点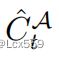与学生网络的预测中心点进行配对。

 若教师网络和学生网络预测的bounding box是一致，各对应元素的距离和应该为0

中心一致损失：

 在集成学习中，教师网络生成学习目标给学生网络进行学习，分别用和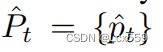表示学生网络和教师网络预测目标类别的可能性。对应的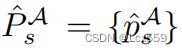基于最小中心距离很容易得到，通过之间的KL散度来定义类感知的一致性损失：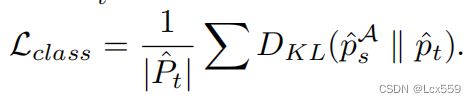

 

 对于学生网络和教师网络对于bounding box大小的预测表示为：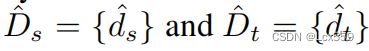

 利用最小中心距离计算得到对应的，之间的均方差误差可以表示为:

 

总的一致性损失可以由这三个损失加权表示得到：