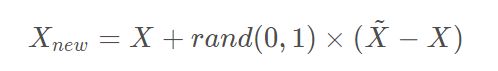机器学习-特征工程中的样本不均衡处理方法
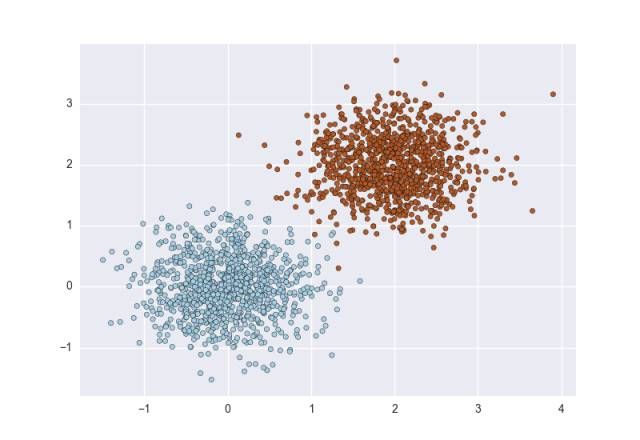
如果你才开始学习机器学习,那么你使用过的数据集很大程度上都是简单、普通、规整的。其中一个原因就是,当你构建分类器时,样本类都是平衡的。在教学中,数据集通常是处理过的,这样才能够把注意力集中在特定算法或技巧上,而不被其它问题干扰。一般情况下,你遇到的样本类似下方的二维图表,其中的点代表样本、点的不同颜色(或形状)代表类:
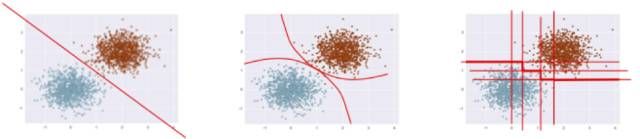
分类算法的目标是尝试学习出一个能够分辨二者的分离器(分类器)。根据不同的数学、统计或几何假设,达成这一目标的方法很多:
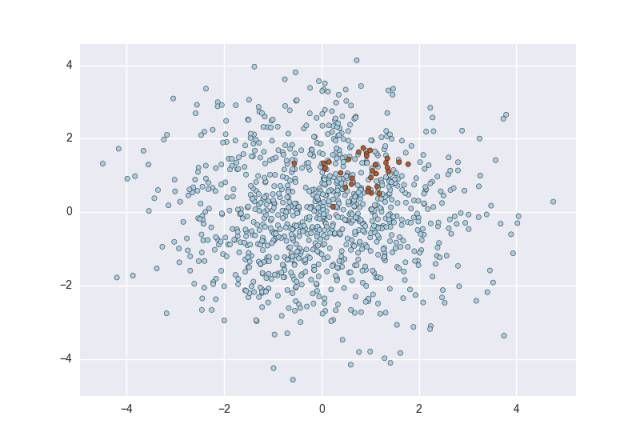
然而,当你开始面对真实的、未加工过的数据时,你会马上注意到,这些数据要嘈杂且不平衡得多。真实数据的散点图看起来更像是这样的:
最主要的问题是这些类是不平衡的:蓝点的数量远超红点。对于不平衡类的研究通常认为「不平衡」意味着少数类只占 10% 到 20% 。而在现实中,数据集甚至能够比上面的例子更加不平衡,比如以下是一些例子:
-
每年,约 2% 的信用卡账户是伪造的。(多数的欺诈检测领域是极其不平衡的);
-
针对某一病征的医学筛查通常涵盖了许多没有此病征的人,以检查出少数患者(例:美国的 HIV 感染率约为 0.4%);
-
每年,硬盘驱动器故障的发生率约为 1%;
-
在线广告的转化率在 10^-3 到 10^-6 的范围区间内;
-
工厂的产品缺陷率一般在 0.1% 左右;
类别不均衡是指在分类学习算法中,不同类别样本的比例相差悬殊,它会对算法的学习过程造成重大的干扰。比如在一个二分类的问题上,有1000个样本,其中5个正样本,995个负样本,在这种情况下,算法只需将所有的样本预测为负样本,那么它的精度(查准率)也可以达到99.5%,虽然结果的精度很高,但它依然没有价值,因为这样的学习算法不能预测出正样本。这里我们可以知道不均衡问题会导致样本较少那一类的高错分率,即较少一类的样本会有较大的比例会被预测成样本数量较多的那一类。
样本不平衡程度的大小不同,解决的难易程度也可能不同,因为问题难易程度还取决于我们所拥有数据有多大。比如在预测癌症诊断的场景中,因为患癌症的人本来就很少,所以数据不但不平衡,样本数还非常少,这样的问题就非常棘手。综上,可以把问题根据难度从小到大排个序:大数据+分布均衡<大数据+分布不均衡<小数据+数据均衡<小数据+数据不均衡。对于需要解决的问题,拿到数据后,首先统计可用训练数据有多大,然后再观察数据分布情况。经验表明,训练数据中每个类别有5000个以上样本,数据量是足够的,正负样本差一个数量级以内是可以接受的,不太需要考虑数据不平衡问题(仅供参考)。
处理不平衡数据,可以从两方面考虑:
一是改变数据分布,从数据层面使得类别更为平衡;
二是改变分类算法,在传统分类算法的基础上对不同类别采取不同的加权方式,使得模型更看重少数类。
一、改变数据分布
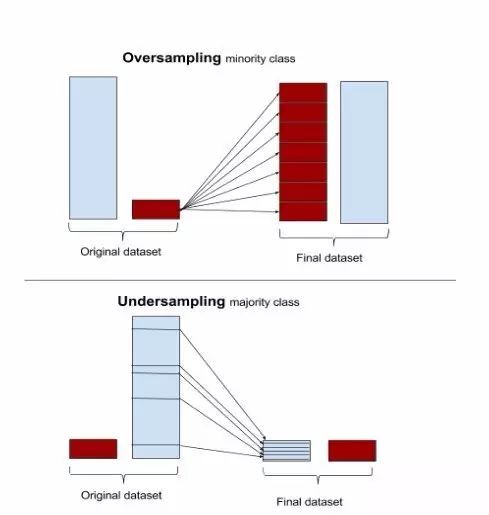
改变数据分布主要是通过对数据进行采样的方法完成,采样分为上采样(过采样)(Oversampling)和下采样(欠采样)(Undersampling),上采样是把小种类复制多份,下采样是从大众类中剔除一些样本,或者说只从大众类中选取部分样本。
通过对数据集的不同的过采样方法,大致可以分为以下四类,具体为:
1. 基础版本的过采样:随机过采样训练样本中数量比较少的数据;缺点,容易过拟合;
2. 改进版本的过采样:SMOTE,通过插值的方式加入近邻的数据点;
3. 基于聚类的过采样:先对数据进行聚类,然后对聚类后的数据分别进行过采样。这种方法能够降低类间和类内的不平衡。
4. 神经网络中的过采样:SGD训练时,保证每个batch内部样本均衡。
1. 随机过采样
通过增加少数类样本数量最简单的方法便是随机复制少数类样本,可以事先设置多数类与少数类最终的数量比例ratio,在保留多数类样本不变的情况下,根据ratio随机复制少数类样本。在使用的过程中为了保证所有的少数类样本信息都会被包含,可以先完全复制一份全量的少数类样本,再随机复制少数类样本使得数量比例满足给定的ratio。
-
优点:操作简单,只依赖于样本分布,不依赖于任何距离信息,属于非启发式方法。
-
缺点:重复样本过多,容易造成分类器的过拟合。
2. SMOTE过采样
SMOTE(Synthetic Minority Oversampling Technique),合成少数类过采样技术.它是基于随机过采样算法的一种改进方案,由于随机过采样采取简单复制样本的策略来增加少数类样本,这样容易产生模型过拟合的问题,即使得模型学习到的信息过于特别而不够泛化,SMOTE算法的基本思想是对少数类样本进行分析并根据少数类样本人工合成新样本添加到数据集中。具体的步骤为:
(1)对于少数类中每一个样本x,以欧氏距离为标准计算它到少数类样本集中所有样本的距离,得到其k近邻。
(2)根据样本不平衡比例设置一个采样比例以确定采样倍率N,对于每一个少数类样本x,从其k近邻中随机选择若干个样本,假设选择的近邻为xn。
(3)对于每一个随机选出的近邻xn,分别与原样本按照如下的公式构建新的样本。
公式为:
SMOTE算法的思想是合成新的少数类样本,合成的策略是对每个少数类样本a,从它的最近邻中随机选一个样本b,然后在a、b之间的连线上随机选一点作为新合成的少数类样本。如图所示:
该算法主要存在两方面的问题:一是在近邻选择时,存在一定的盲目性。从上面的算法流程可以看出,在算法执行过程中,需要确定K值,即选择多少个近邻样本,这需要用户自行解决。从K值的定义可以看出,K值的下限是M值(M值为从K个近邻中随机挑选出的近邻样本的个数,且有M< K),M的大小可以根据负类样本数量、正类样本数量和数据集最后需要达到的平衡率决定。但K值的上限没有办法确定,只能根据具体的数据集去反复测试。因此如何确定K值,才能使算法达到最优这是未知的。
另外,该算法无法克服非平衡数据集的数据分布问题,容易产生分布边缘化问题。由于负类样本的分布决定了其可选择的近邻,如果一个负类样本处在负类样本集的分布边缘,则由此负类样本和相邻样本产生的“人造”样本也会处在这个边缘,且会越来越边缘化,从而模糊了正类样本和负类样本的边界,而且使边界变得越来越模糊。这种边界模糊性,虽然使数据集的平衡性得到了改善,但加大了分类算法进行分类的难度。
3. KMeansSMOTE
KMeansSMOTE采用简单和流行的k-means聚类算法结合SMOTE过采样,以重新平衡数据集。它设法通过仅在安全区域进行过采样来避免产生噪声。此外,它的重点是类别间的不平衡和类别内的不平衡,通过使稀疏的少数类别样本增加来对抗小的分离问题。由于其简单性和kmeans以及SMOTE的广泛可用性,该方法易于实现。它与相关方法的不同之处不仅在于其复杂度低,而且还因为其基于聚类分布生成样本。
KMeansSMOTE包括三个步骤:聚类、过滤和过采样。在聚类步骤中,使用k均值聚类为k个组。过滤选择用于过采样的簇,保留具有高比例的少数类样本的簇。然后,它分配合成样本的数量,将更多样本分配给少数样本稀疏分布的群集。最后,过采样步骤,在每个选定的簇中应用SMOTE以实现少数和多数实例的目标比率。
4. 随机欠采样
减少多数类样本数量最简单的方法便是随机剔除多数类样本,可以事先设置多数类与少数类最终的数量比例ratio,在保留少数类样本不变的情况下,根据ratio随机选择多数类样本。
-
优点:操作简单,只依赖于样本分布,不依赖于任何距离信息,属于非启发式方法。
-
缺点:会丢失一部分多数类样本的信息,无法充分利用已有信息。
5. EasyEnsemble
EasyEnsemble算法是一种有效的不均衡数据分类方法。它将多数类样本随机分成多个子集,每个子集分别与少数类合并,得到多个新的训练子集,并利用每个训练子集训练一个AdaBoost基分类器,最后集成所有基分类器,得到最终的分类器。EasyEnsemble算法有效解决了数据不均衡问题,且减少欠采样造成的多数类样本信息损失。但是,EasyEnsemble算法未考虑少数类样本极度欠缺的情况,由于少数类样本数远小于正确训练分类器所需的样本数,导致基学习器的分类性能差,进而最终的分类器性能也很差。另外,噪声是另一个影响分类器性能的关键因素,在EasyEnsemble算法中并未考虑。
6. 使用K-fold交叉验证
K-fold交叉验证就是把原始数据随机分成K个部分,在这K个部分中选择一个作为测试数据,剩余的K-1个作为训练数据。交叉验证的过程实际上是将实验重复做K次,每次实验都从K个部分中选择一个不同的部分作为测试数据,剩余的数据作为训练数据进行实验,最后把得到的K个实验结果平均。
7. 转化为一分类问题
对于二分类问题,如果正负样本分布比例极不平衡,我们可以换一个完全不同的角度来看待问题:把它看做一分类(One Class Learning)或异常检测(Novelty Detection)问题。这类方法的重点不在于捕捉类间的差别,而是为其中一类进行建模,经典的工作包括One-class SVM等。
二、模型评价方式
谨慎选择AUC作为评价指标:对于数据极端不平衡时,可以观察观察不同算法在同一份数据下的训练结果的precision和recall,这样做有两个好处,一是可以了解不同算法对于数据的敏感程度,二是可以明确采取哪种评价指标更合适。针对机器学习中的数据不平衡问题,建议更多PR(Precision-Recall曲线),而非ROC曲线,具体原因画图即可得知,如果采用ROC曲线来作为评价指标,很容易因为AUC值高而忽略实际对少两样本的效果其实并不理想的情况。
不要只看Accuracy:Accuracy可以说是最模糊的一个指标了,因为这个指标高可能压根就不能代表业务的效果好,在实际生产中,我们可能更关注precision/recall/mAP等具体的指标,具体侧重那个指标,得结合实际情况看。
三、算法选择
(1)选择对数据倾斜相对不敏感的算法。如树模型等。
(2)集成学习(Ensemble集成算法)。首先从多数类中独立随机抽取出若干子集,将每个子集与少数类数据联合起来训练生成多个基分类器,再加权组成新的分类器,如加法模型、Adaboost、随机森林等。
(3)将任务转换成异常检测问题。譬如有这样一个项目,需要从高压线的航拍图片中,将松动的螺丝/零件判断为待检测站点,即负样本,其他作为正样本,这样来看,数据倾斜是非常严重的,而且在图像质量一般的情况下小物体检测的难度较大,所以不如将其转换为无监督的异常检测算法,不用过多的去考虑将数据转换为平衡问题来解决。
四、总结
解决数据不平衡问题的方法有很多,上面只是一些最常用的方法,而最常用的方法也有这么多种,如何根据实际问题选择合适的方法呢?接下来谈谈一些我的经验。
- 在正负样本都非常之少的情况下,应该采用数据合成的方式;
- 在负样本足够多,正样本非常之少且比例及其悬殊的情况下,应该考虑一分类方法;
- 在正负样本都足够多且比例不是特别悬殊的情况下,应该考虑采样或者加权的方法。
- 采样和加权在数学上是等价的,但实际应用中效果却有差别。尤其是采样了诸如Random Forest等分类方法,训练过程会对训练集进行随机采样。在这种情况下,如果计算资源允许上采样往往要比加权好一些。
- 另外,虽然上采样和下采样都可以使数据集变得平衡,并且在数据足够多的情况下等价,但两者也是有区别的。实际应用中,我的经验是如果计算资源足够且小众类样本足够多的情况下使用上采样,否则使用下采样,因为上采样会增加训练集的大小进而增加训练时间,同时小的训练集非常容易产生过拟合。
- 对于下采样,如果计算资源相对较多且有良好的并行环境,应该选择Ensemble方法
参考链接:https://blog.csdn.net/heyongluoyao8/article/details/49408131
参考链接:https://blog.csdn.net/zjx459754206/article/details/81213778
参考链接:https://www.cnblogs.com/charlotte77/p/10455900.html
参考链接:https://mp.weixin.qq.com/s?__biz=MzA3MzI4MjgzMw==&mid=2650718717&idx=1&sn=85038d7c906c135120a8e1a2f7e565ad&scene=0#wechat_redirect