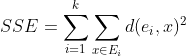K-means聚类算法

目录

简介

对距离的度量及SSE

问题及如何避免

k-means示例

k值选取

肘方法

可视化方法

TSNE

雷达图

---

        总结一些对K-means聚类算法的理解。

        K-means是一种聚类分析方法，聚类分析即是在没有给定划分类别的情况下，根据数据自身的相似度对样本数据进行分组的一种方法。

        K-means也是一种无监督的聚类算法，所谓无监督，即算法需要我们给出分类的数量k，算法本身是不知道需要聚成多少类的（这点可以从K-means的计算步骤看出），即k是K-means 聚类中的超参数，下面先说明K-means的具体内容，再谈k值的选择。

简介

方法名称	K-means
所属方法	聚类分析
监督or非监督	非监督
输入	一组未被标记的样本，即不知道具体分类的样本
依据	数据自身的距离or相似度（常用欧氏距离）
划分原则	组内距离最小，组间距离最大
输出	每个分类的聚类中心，及每个样本的所属分类，本次聚类的SSE
聚类质量判定	误差平方和（SSE）
优点	原理简单；可解释性强；便于处理大量数据
缺点	k值难确定；聚类效果依赖于聚类中心的初始化，导致局部最优；仅能处理连续性数据；对噪音和异常点敏感

对距离的度量及SSE

        对距离的度量常用的方法是欧氏距离，假设样本有p个属性，即，则样本和样本之间的欧氏距离为：

 

        误差平方和SSE是作为聚类质量的判定，公式为：

  

        其中是个聚类中心中的第个聚类中心的聚类中心点。

        即目标是使得k个分类后，每一类中样本与该类的中心的距离尽可能的小，所有样本与其对应的分类中心的距离之和尽可能的小。

        K-means是在最小化误差函数的基础上把数据划分为预先给定的k类，步骤为：

1. 确定聚成k类（业务经验、肘方法等）
2. 从n个样本中随机选取k个对象作为初始的聚类中心
3. 分别计算每个样本到k个聚类中心的距离，将样本分配到距离最近的类中
4. 对所有样本分配结束后，重新计算k个类的聚类中心
5. 与前一次的聚类中心相比较，如果聚类中心发生变化，则转至3，否则转至6
6. 当聚类中心不再发生变化时，停止输出并给出聚类结果

问题及如何避免

问题	解决方法
k值难确定	业务经验、肘方法
聚类效果依赖于聚类中心的初始化，导致局部最优	实践中会多次选择不同的初始聚类中心，多次运行K-means算法
仅能处理连续性数据	离散型数据可以用K-中心点算法，思想类似
对噪音和异常点敏感	提前处理异常数据

k-means示例

 数据样式：

 即数据有三个属性，R、F、M

代码：

import pandas as pd
# 参数初始化
inputfile = r'F:\...\consumption_data.xls'  # 销量及其他属性数据
outputfile = r'F:\...\data_type.xls'  # 保存结果的文件名
k = 3  # 聚类的类别
iteration = 500  # 聚类最大循环次数
data = pd.read_excel(inputfile, index_col = 'Id')  # 读取数据
data_zs = 1.0*(data - data.mean())/data.std()  # 数据标准化

from sklearn.cluster import KMeans
model = KMeans(n_clusters = k, n_init = 4, max_iter = iteration,random_state=1234)  # 分为k类，并发数4
model.fit(data_zs)  # 开始聚类

# 简单打印结果
r1 = pd.Series(model.labels_).value_counts()  # 统计各个类别的数目
r2 = pd.DataFrame(model.cluster_centers_)  # 标准化数据的聚类中心
r2.columns=data.mean().index #修改r2的列，方便逆标准化计算
r_1 = pd.concat([r2*data.std()+data.mean(), r1], axis = 1) # 横向连接（0是纵向），得到聚类中心对应的类别下的数目
r_1.columns = list(data.columns) + ['类别数目']  # 重命名表头
print(r_1)

# 详细输出原始数据及其类别
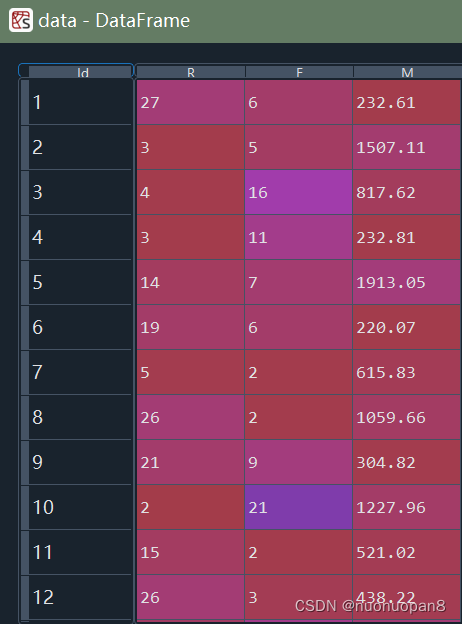
r = pd.concat([data, pd.Series(model.labels_, index = data.index)], axis = 1)   # 详细输出每个样本对应的类别
r.columns = list(data.columns) + ['聚类类别']  # 重命名表头
# r.to_excel(outputfile)  # 保存结果

#同时保存两个结果到xls中
with pd.ExcelWriter(outputfile) as writer:  # doctest: +SKIP
    r_1.to_excel(writer, sheet_name='聚类中心及数目')
    r.to_excel(writer, sheet_name='原始数据聚类类别')


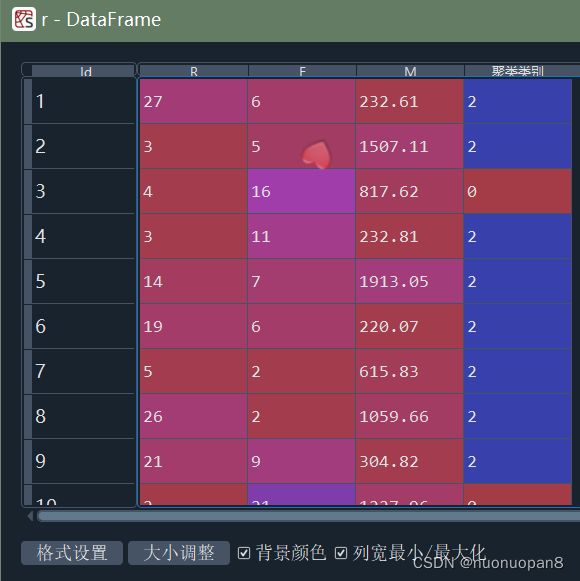
def density_plot(data):  # 自定义作图函数
  import matplotlib.pyplot as plt
  plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
  plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
  p = data.plot(kind='kde', linewidth = 2, subplots = True, sharex = False)
  [p[i].set_ylabel('密度') for i in range(k)]
  plt.legend()
  plt.tight_layout()
  return plt

pic_output = r'F:\...\分群'
# 概率密度图文件名前缀
for i in range(k):
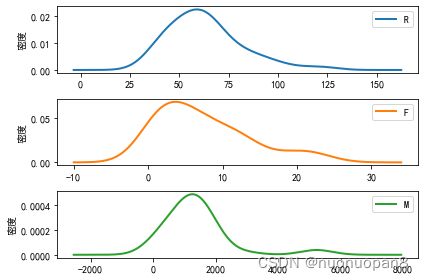
  density_plot(data[r['聚类类别']==i]).savefig('%s%s.png' %(pic_output, i+1))

结果：

①聚类中心和数目

② 原始数据的聚类结果

③每个分类的每个变量的概率密度函数图

 

k值选取

        k值选取：

                1.根据具体业务具体分析（经验）

                2.肘方法--根据具体数据的性质

                3. 轮廓图定量分析法

        k值的选择一方面需要结合具体业务来确定，另一方面可以通过肘方法（下面会有例子）来估计，或者是利用轮廓图定量分析聚类质量（之后再补充）。

肘方法

        肘方法得到的最优参数k是以最小化误差平方和SSE为依据的。K-means使用误差平方和SSE来作为聚类质量的度量，对于两种不同的聚类结果，误差平方和SSE较小的结果更优，SSE是计算每个样本与其所属类别聚类中心的距离的平方，SSE会随着分类k的增加而减小，但随着分类数量k的增大，SSE的值趋于平缓，即分类数量再增加，SSE的也不会改变很大，也就是聚类的质量不会发生显著的提高了。根据这一情况，肘方法选取的k，是SSE发生骤变且骤变之后随着分类数量的增大而趋于平滑的k值。

        肘方法的操作步骤：

                1. 设定不同的k值，计算此k值下的聚类结果质量SSE

                2. 画出k值-SSE图，确定k值

        代码：

d=[]
for i in range(1,11):    #k取值1~11，做kmeans聚类，看不同k值对应的簇内误差平方和
    km=KMeans(n_clusters=i,init='k-means++',n_init=10,max_iter=300,random_state=0)
    km.fit(data_zs)
    d.append(km.inertia_)  #inertia簇内误差平方和

plt.plot(range(1,11),d,marker='o')
plt.xlabel('number of clusters')
plt.ylabel('distortions')
plt.show()

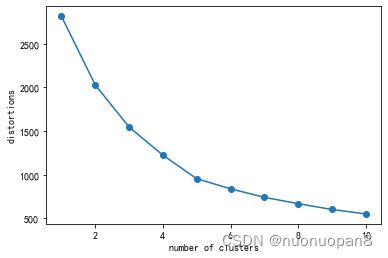
        结果：

        看这个结果，其实选择k=5比较好，k从1到2，从2到3，从3到4，从4到5，误差平方和SSE的减少都相当明显，从5到6，及之后，SSE的减少都有限，所以最佳的k值应该为5。由于上图看上去像一只手肘，理论最佳分类k值在手肘的肘处取得，这也是该方法叫肘方法的缘故。但如果根据具体问题具体分析得到分类k=3比较好，那也可以直接用3分类，肘方法是从数据层面去考虑的一个理论值，在实际操作中需要具体问题具体分析，肘方法可以用于验证3分类也可行，也比较好。

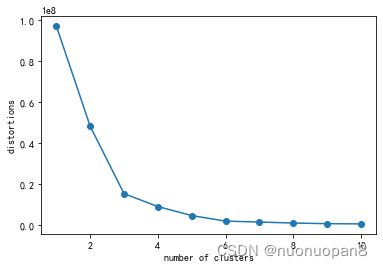
        下面这个肘方法结果图是我做另一个数据分析时的结果，效果更佳好，可以直接看得出SSE的骤变：

可视化方法

        将数据聚类结束后，利用可视化的方式展示分类结果效果更佳。

TSNE

        TSNE是一个聚类结果可视化的工具，其定位是高维数据的可视化。该工具会对数据进行降维，然后展示在二维或三维平面上。

        代码：

import pandas as pd
from sklearn.manifold import TSNE

tsne = TSNE(random_state=105)
tsne.fit_transform(data_zs)  # 用标准化数据进行数据降维
tsne = pd.DataFrame(tsne.embedding_, index = data_zs.index)  # 转换数据格式，tsne.embedding_是降维后得到的数据，把他与原始数据的索引连接在一起(即与原始数据对应)

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

# 不同类别用不同颜色和样式绘图
d = tsne[r['聚类类别'] == 0]  #用原始数据的类别，对应取tsne降维后的结果
plt.plot(d[0], d[1], 'r.')
d = tsne[r['聚类类别'] == 1]
plt.plot(d[0], d[1], 'go')
d = tsne[r['聚类类别'] == 2]
plt.plot(d[0], d[1], 'b*')
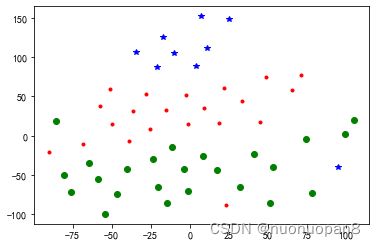
plt.show()

         结果：

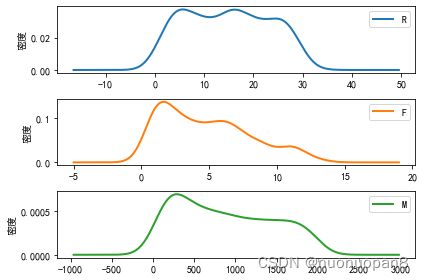
        下面这个结果图是我做另一个数据分析时把20维的变量结果降到到2维平面的结果，说明之前我的分类结果具有较高的准确性，类别非常清晰：

雷达图

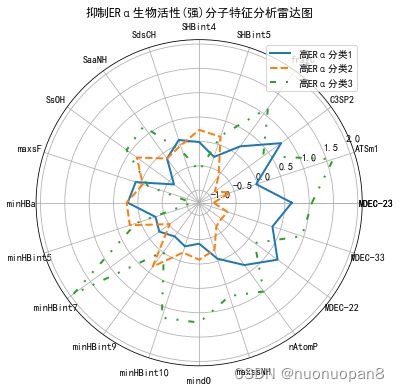
        雷达图可以画出各个聚类中心在不同维度上的值，可以形象化的展示不同类的特点，下图是我比赛时，让给出每个变量的取值范围，但处理数据的时候，画变量的概率密度分布图发现某些变量有两个峰值，不能轻易的认为这些变量就只能有一个小范围的取值，我就对数据进行了一次聚类，利用聚类来区别同一类别不同取值的而形成的新的分类。

        该数据用的是一个20维的数据，与前面使用的数据不同，这里仅展示雷达图显示分类结果的效果。

        代码：

import pandas as pd
cluster_center=r_1.loc[:,col_1]  #这里是取前面计算结果得到的二十维数据
import matplotlib.pyplot as plt
#客户分群雷达图
labels=list(cluster_center.columns)
legen=['高ERα分类'+str(i+1) for i in cluster_center.index] #客户群命名
lstype=['-','--',(0,(3,5,1,5,1,5)),':','-.']
kinds=list(cluster_center.iloc[:,0])
#由于雷达图要保证数据闭合，因此再添加L列，并转换为np.array
a=pd.concat([cluster_center,cluster_center.iloc[:,0]],axis=1)
centers=np.array(a)

#分割圆周长，并让其闭合
n=len(labels)
angle=np.linspace(0,2*np.pi,n,endpoint=False)
angle=np.concatenate((angle,[angle[0]]))
#绘图
fig=plt.figure(figsize=(8,6))
ax=fig.add_subplot(111,polar=True)
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
#画线
for i in range(len(kinds)):
    ax.plot(angle,centers[i],linestyle=lstype[i],linewidth=2,label=kinds[i])
#添加属性标签
labels=labels+list([labels[0]])
ax.set_thetagrids(angle*180/np.pi,labels)
plt.title('抑制ERα生物活性(强)分子特征分析雷达图')
plt.legend(legen)
plt.show()

        结果：