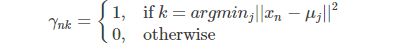kmeans聚类算法python实现、显示折线图_聚类算法kmeans，kmeans++及python实现

1、kmeans

kmeans, k-均值聚类算法，能够实现发现数据集的 k 个簇的算法，每个簇通过其质心来描述。

kmeans步骤：

(1)随机找 k 个点作为质心(种子)；

(2)计算其他点到这 k 个种子的距离，选择最近的那个作为该点的类别；

(3)更新各类的质心，迭代到质心的不变为止。

Q:如何选择 k 值？

A: 根据 k 取不同的值时，模型性能曲线图。

横坐标是聚类数目k，纵坐标是各点到距离中心的距离和。在拐点处的K(距离和下降速率变慢)作为选择的值。

2、kmeans++

因为，kmeans的初始种子的随机找的，这样，算法的收敛快慢与初始值关系非常大，于是，kmeans++ 主要针对初始值的选取进行改进。

初始值选取，如下：

1、也是随机选取一个种子；

2、计算其他点到这个种子的距离；

3、选择这些较大的距离的那个点，替代随机选取的那个种子，作为新的种子点(这里的较大的距离，可以理解为maxDistance*随机数，随机数可以选取0.5-1；)；

4、迭代1-3步，直到选取k个种子为止。

3. 评估聚类效果

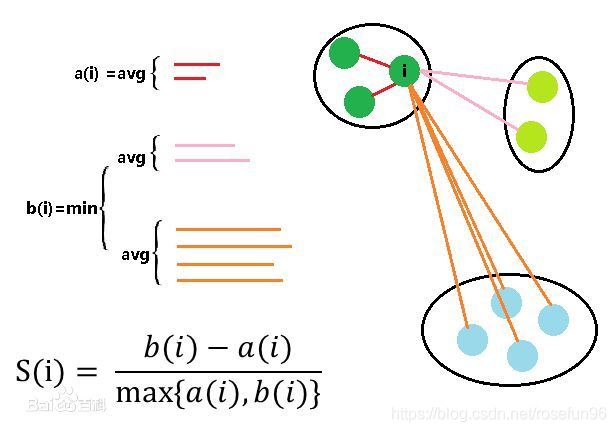
轮廓系数法SC

轮廓系数(Silhouette Coefficient))结合了聚类的凝聚度(Cohesion)和分离度(Separation)，用于评估聚类的效果。该值处于-1~1之间，值越大，表示聚类效果越好。

计算步骤：

(1)选择一个点 ，计算该点 到同一簇内所有其他元素距离的平均值，记为 , 量化簇内的凝聚度；

(2)选择一个其他簇，计算该点到簇内的平均距离。选择该点与其他簇平均距离最小的值，记为 , 用于量化簇间的分离度。

(3)对于样本点，轮廓系数为：

a(i) ：i向量到同一簇内其他点不相似程度的平均值

b(i) ：i向量到其他簇的平均不相似程度的最小值

当轮廓系数<0, 该点可能误分； 值 = 0， 该点在两簇边缘； 值=1， 离其他簇很远。

计算所有点的轮廓系数，求平均值， 即为当前聚类的整体轮廓系数。

因此，轮廓系数可以用来确定Kmean的K值，选取轮廓系数最大的K作为最终的类数目。

(2)误差平方和

4. 其他问题

(1)kmeans一定会收敛吗

kmeans的目标函数：

E步：评估隐变量，每类样本属于的类别

M步：固定数据点的分配，更新参数

由于EM算法具有收敛性，kmeans也会最终收敛。

(2) Kmeans 和KNN的区别

KNN：

分类算法；

监督学习；

数据集是带Label的数据；

没有明显的训练过程，基于Memory-based learning；

K值含义 - 对于一个样本X，要给它分类，首先从数据集中，在X附近找离它最近的K个数据点，将它划分为归属于类别最多的一类

K-means：

聚类算法；

非监督学习；

数据集是无Label，杂乱无章的数据；

有明显的训练过程；

K值含义- K是事先设定的数字，将数据集分为K个簇，需要依靠人的先验知识

不同点：

两种算法之间的根本区别是，K-means本质上是无监督学习，而KNN是监督学习；K-means是聚类算法，KNN是分类(或回归)算法。

K-means算法把一个数据集分割成簇，使得形成的簇是同构的，每个簇里的点相互靠近。该算法试图维持这些簇之间有足够的可分离性。由于无监督的性质，这些簇没有任何标签。KNN算法尝试基于其k(可以是任何数目)个周围邻居来对未标记的观察进行分类。它也被称为懒惰学习法，因为它涉及最小的模型训练。因此，它不用训练数据对未看见的数据集进行泛化。

5. 实践

Kmeans python 代码:

import numpy as np

class KMeans(object):

def __init__(self, n_cluster, epochs=10):

self.n_cluster = n_cluster

self.epochs = epochs

pass

def init_centers(self, X):

idx = np.random.randint(len(X), size=(self.n_cluster,))

centers = X[idx,:]

return centers

def calculate_distance(self,arr1,arr2):

# L2 distance.

distance = np.mean(np.sqrt((arr1-arr2)**2))

return distance

def update_centers(self, X):

predict_class = self.predict(X)

# update centers

centers = self.centers

for ct in range(len(centers)):

idx, = np.where(predict_class == ct)

samples = X[idx, :]

assert len(samples)>0

centers[ct] = np.mean(samples,axis=0)

self.centers = centers

return self.centers

def fit(self, X, y=None):

self.centers = self.init_centers(X)

for epoch in range(self.epochs):

self.centers = self.update_centers(X)

return self.centers

def predict(self,X):

predict_class = np.zeros(shape=(len(X),))

centers = self.centers

for n_sample,arr in enumerate(X):

min_distance = float("inf")

p_class = 0

for ct in range(len(centers)):

distance = self.calculate_distance(arr,centers[ct])

if distance < min_distance:

min_distance = distance

p_class = ct

predict_class[n_sample] = p_class

return predict_class

def score(self, X):

pass复制代码

示例：

定义3个高斯分布。

np.random.seed(1)

data1 = np.random.normal(1, 0.5, size=(100, 2))

np.random.seed(1)

data2 = np.random.normal(4, 0.8, size=(100, 2))

np.random.seed(1)

data3 = np.random.normal(7, 0.8, size=(100, 2))

X = np.concatenate((data1, data2, data3),axis=0)#np.random.randint(10,size=(100,2))

print(X.shape)

kmeans = KMeans(3)

centers = kmeans.fit(X)

print(centers)复制代码

可视化聚类的结果：

# Generate scatter plot for training data

import matplotlib.pyplot as plt

plt.scatter(X[:,0], X[:,1], marker="o", picker=True)

plt.title('Clusters of data')

plt.xlabel('x1')

plt.ylabel('x2')

plt.scatter(centers[:,0], centers[:,1], marker="v", picker=True)

plt.show()复制代码

在这里插入图片描述

参考：

本文使用 mdnice 排版