处理无标签数据的套路：T-SNE与k-means++代码简单实现

背景：当我们在实际工作过程中，我们可能会遇到大量的“无标签”样本数据。针对这个问题，我们可以使用聚类算法进行分类，对每一类的数据进行标注，使“无标签”样本数据转化为“有标签”数据。并通过降维实现数据可视化来检验其效果。

思路：我们可以先随机选取簇的值，将无标签的数据进行聚类，然后在通过Tsne可视化检验其聚类效果。也可以将原数据先进行TSNE降维可视化，看一下降维后的数据分布。根据实际情况设定簇的值，进而使用聚类算法。在实际工作中我们这两种方案可以都尝试以下。

下面我将具体讲述第二种方案的代码实现

一、首先导入相关文件并读取“无标签”数据

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import offsetbox
from sklearn.datasets import load_digits
from sklearn.manifold import TSNE
from sklearn.cluster import KMeans
from sklearn import (manifold, datasets, decomposition, ensemble,
             discriminant_analysis, random_projection)

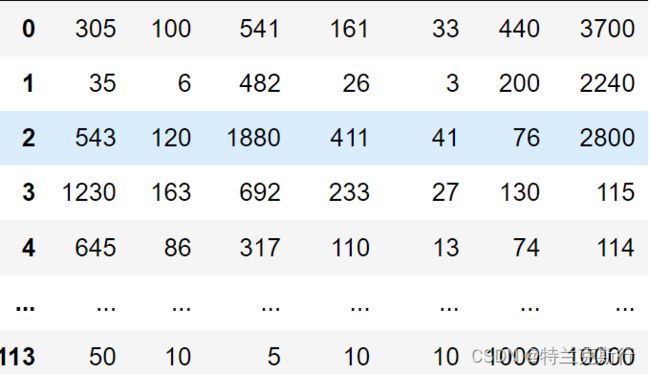
data = pd.read_csv("you.csv")

数据形式如下：

                             

二、使用T-sne对数据进行降维并实现可视化

首先我们需要看清楚sklearn官网的T-SNE参数说明：

n_components	int, optional (default: 2) 嵌入式空间的尺寸。
perplexity	float, optional (default: 30) 困惑与其他流形学习算法中使用的最近邻居的数量有关。较大的数据集通常需要较大的困惑度。考虑选择一个介于5到50之间的值。不同的值可能会导致明显不同的结果。
early_exaggeration	float, optional (default: 12.0) 控制原始空间中自然簇在嵌入式空间中的紧密程度以及它们之间有多少空间。对于较大的值，自然簇之间的空间在嵌入式空间中会更大。同样，此参数的选择不是很关键。如果成本函数在初始优化过程中增加，则早期夸张因子或学习率可能会太高。
learning_rate	float, optional (default: 200.0) t-SNE的学习率通常在[10.0，1000.0]范围内。如果学习率太高，则数据看起来可能像“球”，其任何一点都与其最近的邻居等距。如果学习率太低，则大多数点可能看起来像是密集的云，几乎没有异常值。如果成本函数陷入不良的局部最小值中，则提高学习率可能会有所帮助。
n_iter	int, optional (default: 1000) 优化的最大迭代次数。至少应为250。
n_iter_without_progress	int, optional (default: 300) 在中止优化之前没有进度的最大迭代次数，在250次具有早期夸张的初始迭代之后使用。请注意，仅每50次迭代检查一次进度，因此此值将四舍五入到50的下一个倍数。 0.17版中的新功能：参数n_iter_without_progress用于控制停止条件。
min_grad_norm	float, optional (default: 1e-7) 如果梯度范数低于此阈值，则优化将停止。
metric	string or callable, optional 计算要素阵列中实例之间的距离时使用的度量。如果metric是字符串，则它必须是scipy.spatial.distance.pdist为其metric参数允许的选项之一，或者是pairwise.PAIRWISE_DISTANCE_FUNCTIONS中列出的度量标准。如果度量是“预先计算的”，则假定X为距离矩阵。或者，如果metric是可调用的函数，则在每对实例（行）上调用metric，并记录结果值。可调用对象应将X的两个数组作为输入，并返回一个指示它们之间距离的值。默认值为“欧几里得距离”，它被解释为平方的欧几里得距离。
init	string or numpy array, optional (default: “random”) 嵌入的初始化。可能的选项是“ random”，“ pca”和一个numpy数组（n_samples，n_components）。PCA初始化不能用于预先计算的距离，且通常比随机初始化更全局稳定。
verbose	int, optional (default: 0) 详细程度。
random_state	int, RandomState instance, default=None 确定随机数生成器。在多个函数调用之间传递int以获得可重复的结果。注意，不同的初始化可能导致成本函数的局部最小值。请参阅：term: Glossary .
method	string (default: ‘barnes_hut’) 默认情况下，梯度计算算法使用在O（NlogN）时间内运行的Barnes-Hut近似。method='exact'将在O（N^2）时间内运行速度较慢但精确的算法。当最近邻误差大于3%时，应采用精确算法。然而，精确的方法不能扩展到数百万个例子。 版本0.17中的新功能：通过Barnes-Hut的近似优化方法。
angle	float (default: 0.5) 仅在method ='barnes_hut'时使用。这是Barnes-Hut T-SNE在速度和精度之间的权衡。“angle”是从点开始测量的远距离节点的角度大小（在[3]中称为theta）。如果该大小小于“angle”，则将其用作其中包含的所有点的汇总节点。此方法对此参数在0.2-0.8范围内的变化不太敏感。小于0.2的角度会迅速增加计算时间，大于0.8的角度会迅速增加误差。
n_jobs	int or None, optional (default=None) 为邻居搜索运行的并行作业数。当metric="precomputed"或（metric="euclidean"和method="exact"）时，此参数不起作用。None除非在joblib.parallel_backend环境中，否则表示1 。 undefined表示使用所有处理器。有关更多详细信息，请参见词汇表。 0.22版中的新功能。

#定义T-sne函数
def tsne(data,n):
    tsne=TSNE(random_state=42,perplexity=n)###使用fit_transform而不是fit,因为TSNE没有transform方法
    digits_tsne=tsne.fit_transform(data)###运行时间较久
    return digits_tsne

#实现T-sne降维与数据可视化
tsne_data = tsne(data,15)
plt.scatter(tsne_data[:, 0], tsne_data[:, 1])
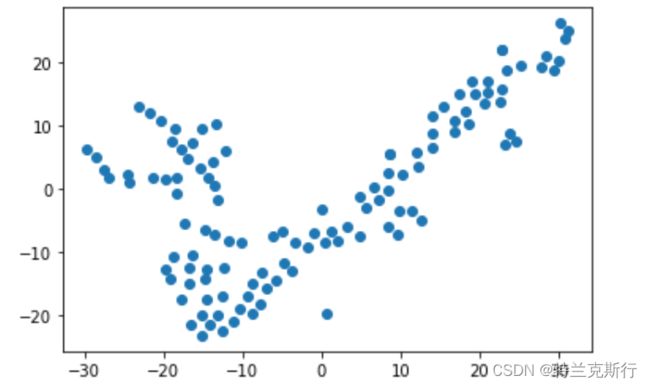
plt.show()

降维后的数据形式如下：

 可视化：

 根据可视化的结果我们可以对接下来的聚类算法设定K值，你们认为是多少？我觉得可以是3或是4或是5.

三、使用k-means++算法进行标注

（1）k-means概述

　在scikit-learn中，包括两个K-Means的算法，一个是传统的K-Means算法，对应的类是KMeans。另一个是基于采样的Mini Batch K-Means算法，对应的类是MiniBatchKMeans。一般来说，使用K-Means的算法调参是比较简单的。用KMeans类的话，一般要注意的仅仅就是k值的选择，即参数n_clusters；如果是用MiniBatchKMeans的话，也仅仅多了需要注意调参的参数batch_size，即我们的Mini Batch的大小。当然KMeans类和MiniBatchKMeans类可以选择的参数还有不少，但是大多不需要怎么去调参。下面我们就看看KMeans类的一些主要参数。

（2）KMeans类主要参数

　　　　1) n_clusters: 即我们的k值，一般需要多试一些值以获得较好的聚类效果。k值好坏的评估标准在下面会讲。

　　　　2）max_iter： 最大的迭代次数，一般如果是凸数据集的话可以不管这个值，如果数据集不是凸的，可能很难收敛，此时可以指定最大的迭代次数让算法可以及时退出循环。

　　　　3）n_init：用不同的初始化质心运行算法的次数。由于K-Means是结果受初始值影响的局部最优的迭代算法，因此需要多跑几次以选择一个较好的聚类效果，默认是10，一般不需要改。如果你的k值较大，则可以适当增大这个值。

　　　　4）init： 即初始值选择的方式，可以为完全随机选择'random',优化过的'k-means++'或者自己指定初始化的k个质心。一般建议使用默认的'k-means++'。

　　　　5）algorithm：有“auto”, “full” or “elkan”三种选择。"full"就是我们传统的K-Means算法， “elkan”是我们原理篇讲的elkan K-Means算法。默认的"auto"则会根据数据值是否是稀疏的，来决定如何选择"full"和“elkan”。一般数据是稠密的，那么就是 “elkan”，否则就是"full"。一般来说建议直接用默认的"auto"

#定义kmeans函数
def kmeans(data,n):
    y_pred = KMeans(n_clusters=n,random_state=10).fit_predict(data)
    return y_pred

#通过kmeans进行聚类
from sklearn import metrics
kmeans_data = kmeans(tsne_data,5)
#现在我们可以用Calinski-Harabasz Index评估的聚类分数，值越大越好
metrics.calinski_harabasz_score(tsne_data, kmeans_data)  

calinski_harabasz_score的值：

k = 3:    219.98599111109104

k= 4:     316.9300725858647

k = 5:    300.64883914453355

由此可知，k为4效果相对较好，我们进行可视化看看具体效果：

#将数据绘制成文本散点
colors=["#476A2A","#7851B8","#BD3430","#4A2D4E","#875525","#A83683","#4E656E","#853541","#3A3120","#535D8E"]
plt.rcParams['font.sans-serif'] = ['SimHei']###防止中文显示不出来
plt.rcParams['axes.unicode_minus'] = False###防止坐标轴符号显示不出来
def plot(digits_tsne, digits_target):
    x_min, x_max = np.min(digits_tsne, 0), np.max(digits_tsne, 0)
    digits_tsne = (digits_tsne - x_min) / (x_max - x_min)
    plt.figure(figsize=(10,10))
    plt.xlim(digits_tsne[:,0].min(),digits_tsne[:,0].max())
    plt.ylim(digits_tsne[:,1].min(),digits_tsne[:,1].max())
    for i in range(len(digits_tsne)):
          plt.text(digits_tsne[i,0],
                     digits_tsne[i,1],
                     str(digits_target[i]),
                     color=colors[digits_target[i]],
                     fontdict={"weight":"bold","size":9})
    plt.xlabel("第一分量")
    plt.ylabel("第二分量")
    
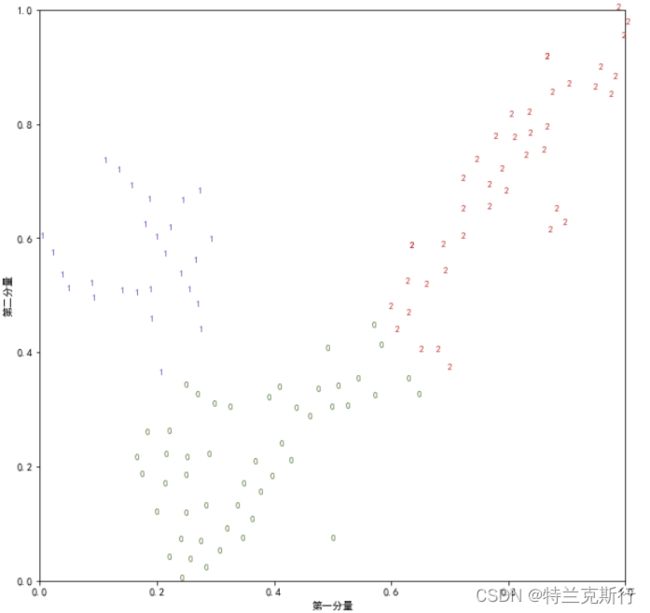
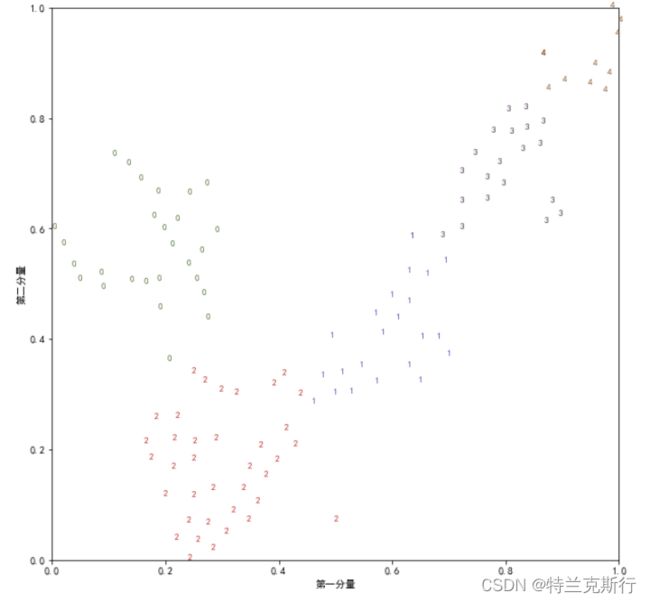
plot(tsne_data,kmeans_data)

k=3:

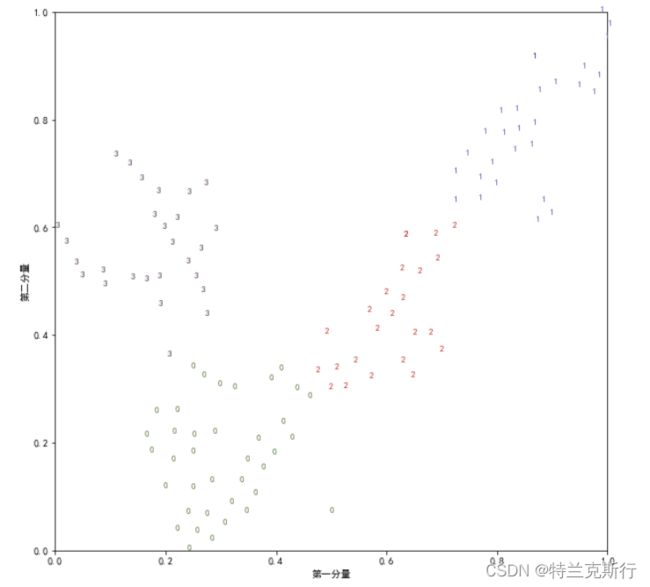
k=4:

 

k =5:

 

 结合上面的可视化结果，设k为3或4都是还很不错的。如果不满意可以试试更多的值。

经过以上三个步骤，我们就可以将无标签数据人为的转换为有标签数据,每个样本的标签储存在kmeans_data中。下面是k=5时的标签：

array([1, 1, 1, 2, 2, 3, 0, 0, 2, 2, 2, 0, 0, 1, 2, 0, 1, 1, 2, 2, 0, 1,
       2, 2, 2, 1, 1, 0, 1, 1, 0, 0, 0, 3, 2, 2, 2, 2, 2, 0, 2, 0, 2, 2,
       4, 1, 4, 4, 0, 2, 0, 2, 2, 2, 2, 0, 3, 3, 3, 0, 0, 1, 2, 3, 3, 0,
       0, 1, 4, 0, 4, 2, 0, 1, 4, 0, 1, 0, 0, 2, 0, 2, 2, 2, 2, 2, 3, 3,
       0, 1, 3, 2, 3, 4, 1, 3, 4, 3, 3, 3, 1, 3, 4, 1, 3, 4, 1, 3, 3, 1,
       4, 0, 2, 3, 2, 1, 2, 2])

参考：无监督学习——流形学习（t-SNE）_yb705的博客-CSDN博客_流形学习代码用scikit-learn学习K-Means聚类 - 刘建平Pinard - 博客园 (cnblogs.com)