A Unified Objective for Novel Class Discovery
2021/9/14
NCD:通过一个没有类重叠的标记数据集训练模型,以对一个无标记的数据集进行聚类,从而发现无标记数据集中的新的类别。文章通过logit连接的方式,对伪标签和ground truth使用一个统一的交叉熵损失函数对模型进行训练,简化了训练流程并大幅提升了效果。
论文地址:https://arxiv.org/abs/2108.08536
Github:https://github.com/DonkeyShot21/UNO
参考:
representation learning与clustering的结合(1)
arXiv:1901.00544
NCD(Novel Class Discovery)新类发现
课题起源于论文Multi-class Classification without Multi-class Labels,文中通过估计为标记样本的成对相似性,通过利用两两相似度来训练聚类网络,以识别无标记数据集中的新类,解决无多类标签的多类别分类任务,由这篇文章开始,NCD成为了一个新的课题。
背景:
- 通过利用包含不同但相关类的标记集的先验知识来推断未标记集中的新对象类别。
- 网络受益于在标记集上可用的监督信号,以学习丰富的图像表示,可以转移到发现未标记集中的未知类 。
- 在训练时,数据被分割成一组标记图像和一组未标记图像(假设类集不相交)。这两组训练集同时用来训练单个网络来对已知类和未知类进行分类。
- 本文的重点在于,生成效果足以跟ground truth一同处理的pseudo-labels。
总体结构
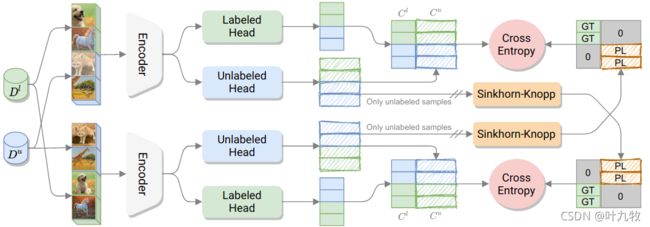
- 文章提出了一个通过单个损失函数来消除自监督的预训练步骤,并统一所有的训练目标(如图1所示)的方法。具体来说,使用多视图自标记策略,生成可以用ground-truth标签同源处理的伪标签。这使得在标记集和未标记集上使用统一的交叉熵损失成为可能。给定一个Batch的图像,使用随机转换生成每个图像的两个视图。网络预测了每个视图的所有类(标记为+未标记)的概率分布。这将产生了两个独立Batch的子集,由于是同一张图片的不同数据增强结果,因此每个视图都可以作为其他视图的伪标签。然后结合ground-truth和伪标签,向网络提供反馈并更新其参数。
方法
数据准备
在NCD任务中,训练数据被分为两组:
- 标记数据集: D l = { ( x 1 l , y 1 l ) , . . . , ( x N l , y N l ) } D^l=\lbrace (x_1^l,y_1^l), ... ,(x_N^l, y_N^l) \rbrace Dl={(x1l,y1l),...,(xNl,yNl)}
- 无标记数据集: D u = { x 1 u , . . . , x M u } D^u=\lbrace x_1^u, ...,x_M^u \rbrace Du={x1u,...,xMu}
定义 C l C^l Cl为标记数据集中的类别而 C u C^u Cu为无标记数据集中的类别,任务的目标是通过 D u D^u Du来发掘 C u C^u Cu个聚类,而 C u C^u Cu是先验的,而 C l C^l Cl与 C u C^u Cu不相交。在测试时,模型的目标是对标记类和未标记类对应的图像进行分类。我们将这个问题表述为学习从图像域到完整标签集的映射: Y = { 1 , . . . , C l , . . . , C l + C u } Y=\lbrace 1, ...,C^l,...,C^l + C^u \rbrace Y={1,...,Cl,...,Cl+Cu}。总体结构图如图2所示。
Unified Objective
为了解决NCD问题,作者提出训练一个由θ参数化的神经网络 f θ ( x ) = { p ( y ∣ x ) ; y ∈ Y } f_θ(x)= \lbrace p(y|x);y\in Y \rbrace fθ(x)={p(y∣x);y∈Y}。它由一个共享的编码器E和两个头h和g组成。
- 其中编码器E是一个标准的后接平均池化层的卷积网络(CNN),用于编码图像的特征:
z = E ( x ) , z ∈ R k z = E(x), z\in \mathbb{R^k} z=E(x),z∈Rk - head h 是一个具有 C l C^l Cl个输出神经元的线性分类器。
- head g 使用了一个多层感知机(MLP),它将 z z z投影到一个低维表示 z ′ z' z′,然后接入一个有 C u C^u Cu输出的线性分类器。
由h和g产生的logits l h ∈ R C l l_h\in\mathbb{R}^{C^l} lh∈RCl与 l g ∈ R C u l_g\in\mathbb{R}^{C^u} lg∈RCu进行concat得到 l = [ l h , l g ] l=[l_h,l_g] l=[lh,lg]。将它们输入到共享的softmax层σ,输出完整标签集的后验分布 Y : p = σ ( l / τ ) Y:p=σ(l/\tau) Y:p=σ(l/τ),其中τ是softmax的温度参数。得到了p的概率分数之后,我们就可以使用标准的交叉熵来训练整个网络:
l ( x , y ) = − Σ c = 1 C y c l o g ( p c ) (1) l(x,y)=-\Sigma_{c=1}^Cy_clog(p_c)\tag{1} l(x,y)=−Σc=1Cyclog(pc)(1)
其中, C = C l + C u C=C^l+C^u C=Cl+Cu,针对 x ∈ D l x\in D^l x∈Dl与 x ∈ D u x\in D^u x∈Du对y进行zero-padding,如下所示:
y = { [ y l , 0 C u ] x ∈ D l [ 0 C l , y ^ ] x ∈ D u (2) y=\left\{ \begin{array}{c} [y^l,0_{C^u}] & x \in D^l \\ [0_{C^l},\hat{y}] & x \in D^u \end{array} \right. \tag{2} y={[yl,0Cu][0Cl,y^]x∈Dlx∈Du(2)
这里, 0 C u 0_{C^u} 0Cu和 0 C l 0_{C^l} 0Cl分别表示维度为 C u C^u Cu和 C l C^l Cl的零向量,依据是已知类与未知类互相之间不重合。
Multi-view and Pseudo-labeling
Multi-view
本节中介绍了如何利用多视图策略来为统一目标生成伪标签。给定一个图像x,作者采用常见的数据增强技术,包括对x应用随机裁剪和颜色抖动,得到x的两个不同的“视图”(v1,v2),它们被调整到原始大小并输入给f。
如果 ( x , y l ) ∈ D l (x,y^l)\in D^l (x,yl)∈Dl,即样本x属于标记数据集,则 y 1 = y 2 = [ y l , 0 C u ] y_1=y_2=[y^l,0_{C^u}] y1=y2=[yl,0Cu],另一方面,如果 x ∈ D u x \in D^u x∈Du,则使用由v1与v2计算得到的 y 1 ^ \hat{y_1} y1^与 y 2 ^ \hat{y_2} y2^与 0 C l 0_{C^l} 0Cl进行concat操作,这样一来,公式(1)就可以独立地应用于每个视图。
然而,这种方法并不鼓励网络对同一图像的不同视图输出一致的预测。为了强制执行这个目标,作者使用了交换的预测任务:
l ( v 1 , y 2 ) + l ( v 2 , y 1 ) (3) l(v_1,y_2)+l(v_2,y_1)\tag{3} l(v1,y2)+l(v2,y1)(3)
Pseudo-labeling
Label assignment
关于伪标签计算,一个常规的获取视图 v 1 v_1 v1的伪标签 y 1 ^ \hat{y_1} y1^的方法是直接使用g来预测编码器E产生的特征图 z 1 = E ( v 1 ) z_1=E(v_1) z1=E(v1),从而得到 g ( z 1 ) = l g 1 g(z_1)=l_g^1 g(z1)=lg1,然后进行softmax操作得到 p g 1 = σ ( l g 1 / τ ) p_g^1=\sigma(l_g^1/\tau) pg1=σ(lg1/τ),最后令 y 2 ^ = p g 1 \hat{y_2}=p_g^1 y2^=pg1并代入公式(2)的计算中。然而,文献[27]中观察到这样的伪标签设置会导致退化,具体来说就是对于任何不同的inputs,g总是给出相同的logits vector。
为了解决这个问题,论文Self-labelling via simultaneous clustering and representation learning中详细的论述了使用label assignment进行聚类并求解伪标签的方法。方法与DeepCluster类似,DeepCluster的结构如图3所示。
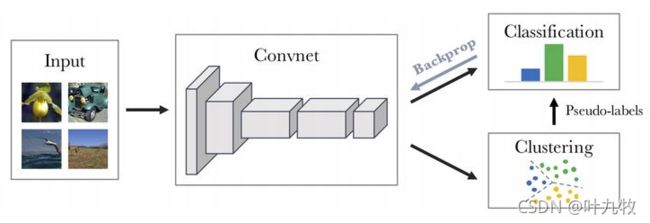
- 用已有的clustering算法,如K-means去获得Pseudo-labels,见上图,然后去supervise学习representation,这就是DeepCluster。但clustering获得的labels毕竟不是100%的正确,所以这种naively的结合,会出现一些问题,比如,将所有的样本都归为同一类。
- 解决思路是加了一个constraint,labels必须要对所有的样本平均分配,即是最大化样本的indices和labels间的information。
- 考虑 x = Φ ( I ) x=\Phi(I) x=Φ(I)将图片I映射到特征向量 x ∈ R D x\in \mathbb{R^D} x∈RD,则N的数据点 I 1 , . . . , I N I_1,...,I_N I1,...,IN对应的labels为 y 1 , . . . , y N ∈ { 1 , . . . , K } y_1,...,y_N \in \lbrace 1,...,K \rbrace y1,...,yN∈{1,...,K},通常将一个线性分类器用于将特征向量转化为class score,表述为 h : R D → R K h:\mathbb{R^D} \rightarrow \mathbb{R^K} h:RD→RK,class score再通过softmax映射为probabilities
p ( y = ⋅ ∣ x i ) = s o f t m a x ( h ( Φ ( x i ) ) ) p(y=\cdot|x_i)=softmax(h(\Phi(x_i))) p(y=⋅∣xi)=softmax(h(Φ(xi))) - 模型参数使用cross-entropy loss学习得到公式(4):
E ( p , q ) = − 1 N ∑ i = 1 N l o g p ( y i ∣ x i ) (4) E(p,q)=-{{1} \over {N}}\sum_{i=1}^Nlogp(y_i|x_i)\tag{4} E(p,q)=−N1i=1∑Nlogp(yi∣xi)(4)
但在fully unsupervised的情况下,最关键要解决的问题是:最小化上式将会导致模型对于所有的数据点都输出一个单一的(任意的)label。 - 为了解决这个问题,首先将labels表示为后验(posterior)分布 q ( y ∣ x i ) q(y|x_i) q(y∣xi),并将公式(4)重写为:
E ( p , q ) = − 1 N ∑ i = 1 N ∑ y = 1 k q ( y ∣ x i ) l o g p ( y ∣ x i ) (5) E(p,q)=-{1 \over N} \sum _{i=1} ^N \sum _{y=1} ^k q(y|x_i)logp(y|x_i)\tag{5} E(p,q)=−N1i=1∑Ny=1∑kq(y∣xi)logp(y∣xi)(5)
其实就是计算p和q的交叉熵,如果将后验 q ( y ∣ x i ) = δ ( y − y i ) q(y|x_i)=\delta(y-y_i) q(y∣xi)=δ(y−yi),即使用one-hot表示,则公式(4)等同于公式(5),有 E ( p , q ) = E ( p ∣ y i , . . . , y N ) E(p,q)=E(p|y_i,...,y_N) E(p,q)=E(p∣yi,...,yN),因此优化 q ( y ∣ x i ) q(y|x_i) q(y∣xi)实际上等同于标签再分配(reassign labels),如果对q不加限制,则必然导致退化的结果。 - 因此对q作出限制:整个dataset中,每一类的数量必须是一样的,即labels对dataset进行均分,则目标函数可以写为:
min p , q E ( p , q ) s u b j e c t t o ∀ y : q ( y ∣ x i ) ∈ { 0 , 1 } a n d ∑ i = 1 N q ( y ∣ x i ) = N K (6) \min_{p,q}E(p,q) \quad subject \ to \quad \forall y:q(y|x_i) \in \lbrace 0,1 \rbrace \ and \ \sum _{i=1} ^N q(y|x_i) = {N \over K} \tag{6} p,qminE(p,q)subject to∀y:q(y∣xi)∈{0,1} and i=1∑Nq(y∣xi)=KN(6)
为了方便观察,令 P y i = p ( y ∣ x i ) 1 N P_{y_i}=p(y|x_i){1 \over N} Pyi=p(y∣xi)N1,由模型估算出的 K × N K \times N K×N联合概率分布(joint probabilities)矩阵,K为类的数量,N为样本数量; Q y i = q ( y ∣ x i ) 1 N Q_{y_i}=q(y|x_i){1 \over N} Qyi=q(y∣xi)N1,这是assign的 K × N K \times N K×N联合概率分布矩阵,则矩阵Q可表示为:
U ( r , c ) : = { Q ∈ R + K × N ∣ Q 1 = r , Q T 1 = c } r = 1 K ⋅ 1 c = 1 N ⋅ 1 (7) U(r,c):=\lbrace Q \in \mathbb{R_+}^{K \times N}|Q1=r,Q^T1=c \rbrace \\ r={1 \over K} \cdot 1 \tag{7} \\ c={1 \over N} \cdot 1 U(r,c):={Q∈R+K×N∣Q1=r,QT1=c}r=K1⋅1c=N1⋅1(7)
1是全1的向量,其维度由 Q Q Q决定,所以r和c是Q在列和行上的边缘投影。
UNO中的伪标签计算
回到UNO中,设 L = [ l g 1 , . . . , l g B ] L=[l_g^1,...,l_g^B] L=[lg1,...,lgB],其列是由g对B大小的mini-batch图像计算的logits。设 Y ^ = [ y 1 ^ , . . . , y B ^ ] \hat{Y}=[\hat{y_1},...,\hat{y_B}] Y^=[y1^,...,yB^],其行是当前batch处理的未知伪标签的矩阵,同时,作者添加了一个熵项 H ( Y ) H(Y) H(Y),它惩罚所有logits相等的情况。则可以将任务转化为:
Y ^ = max Y ∈ Γ T r ( Y L ) + ϵ H ( Y ) Γ = { Y ∈ R + C u × B ∣ Y 1 B = 1 C u × 1 C u , Y T 1 C u = 1 B × 1 B } (8) \hat{Y}=\max _{Y \in \Gamma}Tr(YL)+ \epsilon H(Y) \\ \Gamma = \lbrace Y \in \mathbb{R_+}^{C^u \times B}|Y1_B={1 \over C^u} \times 1_{C^u},Y^T1_{C^u}={1 \over B} \times 1_B \rbrace \tag{8} Y^=Y∈ΓmaxTr(YL)+ϵH(Y)Γ={Y∈R+Cu×B∣Y1B=Cu1×1Cu,YT1Cu=B1×1B}(8)
其中, ϵ > 0 \epsilon > 0 ϵ>0是超参数, T r Tr Tr是迹函数,有: ∑ i , j Y i j ⋅ L i j \sum_{i,j}Y_{ij} \cdot L_{ij} ∑i,jYij⋅Lij,即对矩阵逐点相乘求和。 H H H是一个用于散射伪标签的熵函数,这样的条件强制每个聚类中心平均在一个batch中被选择 B u C u B^u \over C^u CuBu次, B u B^u Bu是一个batch中的无标记样本数量。公式(8)中, Γ \Gamma Γ又称为运输多面体(transportation polytope),可以用Sinkhorn-Knopp算法进行求解。
过度聚类Overclustering
为了提高聚类性能,作者结合主要的聚类任务,采用了过度聚类(强制f生成一个更细粒度的未标记数据的另一个分区),这能够提高特征表示的质量。与E相连的过度聚类头o与g相似,但是有 K = C u × m K=C^u \times m K=Cu×m个聚类输出。
作者还尝试使用了多个聚类头 ( g 1 , . . . , g n ) (g_1,...,g_n) (g1,...,gn)与 ( o 1 , . . . , o n ) (o_1,...,o_n) (o1,...,on)通过使用多个头,增加了反向传播到网络共享部分的整体信号。在训练时,对于给定的一个batch数据,对 g 1 , . . . , g n g_1,...,g_n g1,...,gn进行迭代,对 g i g_i gi与 h ( l h ) h(l_h) h(lh)产生的logits进行concat连接,然后将结果送入到一个 C l + C u C^l + C^u Cl+Cu的Softmax中,并计算交叉熵损失函数。 o j o_j oj也同样进行类似的操作,接入一个 C l + K C^l + K Cl+K输出的softmax层。
实验部分
数据集设置
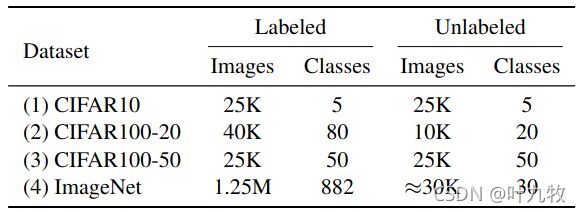
- 上图展示了本文实验中采用的数据集,每个数据集中的类别和标注图片数量
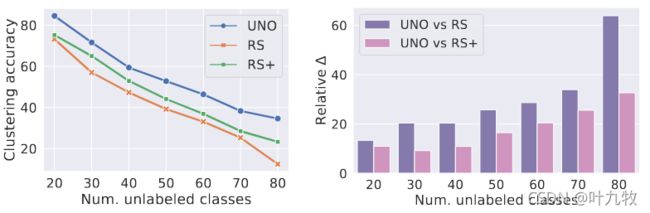
消融实验
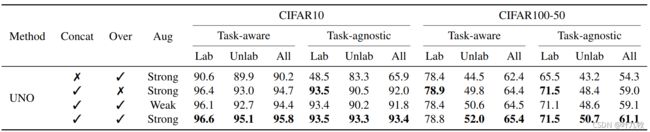
- 上图为消融实验的结果,验证每个模块的有效性。
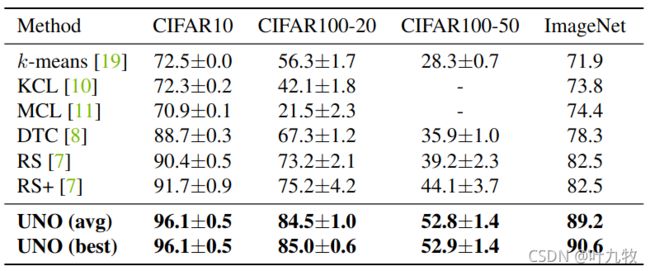
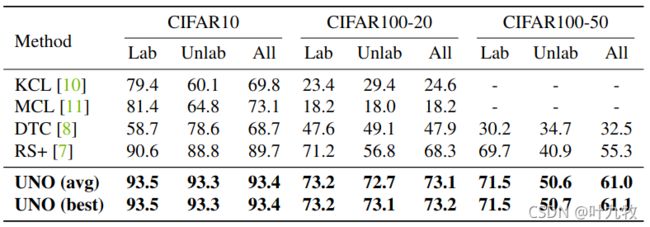
Comparison with the state-of-the-art
- 未标注数据类型上,不同数据集中,UNO和其他SOTA方法的性能对比。
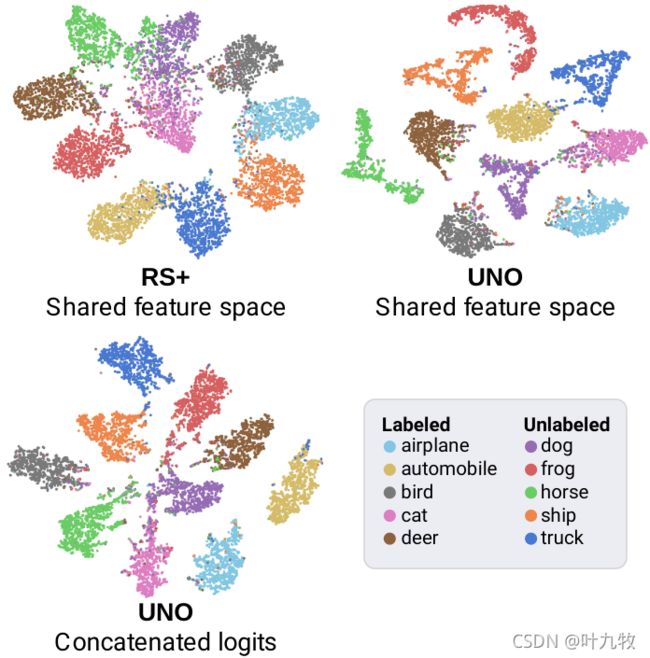
- 可视化共享的特征空间和头h和g的concat logit的聚类结果。