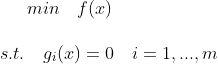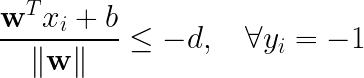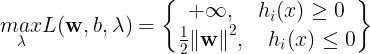机器学习之四：支持向量机——理论框架
由于SVM的理论实在太过深奥，因此这一部分的内容分为了理论、SMO算法详解和实战三个部分，以显得更有条理，也方便大家消化。
一、前置知识
1.1 KKT条件
KKT条件是非线性规划最优解的必要条件。
先从拉格朗日乘数法说起，拉格朗日乘数法是高数里的知识，相信大部分人都学过，并且KKT条件是拉格朗日乘数法的泛化情况，因此从拉格朗日乘数法入手能够比较通俗易懂。
对于如下的优化问题：
定义拉格朗日函数：
然后令其偏导等于求得最优解的必要条件：
如果我们现在面对着一个有着非等式约束的优化问题，如下所示：
定义拉格朗日函数：
可以通过以下的公式求解：
这些公式便叫做KKT条件，求得的解中必有一个是原问题的最优解。至于为什么会这样，感兴趣的同学可以移步https://www.cnblogs.com/liaohuiqiang/p/7805954.html。 本文限于篇幅，就不介绍其原理了。
1.2 拉格朗日对偶性
以二元函数 
举例，我们有 
, 直观点说就是最大值中的最小值都比最小值中的最大值要大。证明如下：
证：令 
分别是
的最优解，我们有
. 证明完毕。
这叫做弱对偶性。我们令 
为
的最优值， 
为
的最优值，二者相等叫做强对偶性。想要强对偶性成立，需要满足以下两个条件：
1. 原问题为凸优化
2. 最优解满足KKT条件
关于强对偶性与这两个条件的关系，由于涉及运筹学的知识，在这里超纲了。感兴趣的同学可以自行了解下。如果不感兴趣，记住结论即可，对于我们理解SVM已经够用了。
二、SVM
2.1 基本概念
1. 超平面：超平面是用来分隔空间的“东西”。比如对于二维平面，我们可以用一条直线将其分割；对于三维空间，我们可以用一个平面将其分割；而对于更高维的空间，我们用来将其分隔的“东西”统一称为超平面。
2. 数据的线性可分：对于一组有两个类别的数据，如果存在一个超平面，可以将这两类完全分开，则称这组数据是线性可分的。
3. 支持向量：距离超平面最近的那些点称作支持向量。
4. 数据类别：在其他二分类的分类器中，两种数据类别分别用0和1来表示。在SVM中，我们用+1和-1来表示两种类别。这种表示只是更方便处理，不会对结果产生任何影响。
此外，如果大家看其他介绍SVM的文章或者视频可能会看到“函数间隔”和“几何间隔”这些词，由于笔者认为没有这些概念也可以理解SVM，所以本文就不再介绍了。
2.2 SVM目标
我们以二维平面为例。如下图所示，平面有两类点，分别用X和O表示。现有三条直线l1，l2，l3，都可以将这两类数据分开，那么哪一条直线更好呢？从直观上来说，我们认为 l1 更好，因为它到两类数据的距离更大，图中红色的虚线就是第一类数据分别到l1，l2，l3的距离。SVM干的就是这样一件事：找到这样一个超平面，使得这个超平面到两类数据的距离最大。
那么，如何定义这个“距离”呢？ 对于一个超平面 
，点
到其的距离为
. 这个公式其实是高中的内容，它是点到直线的距离在更高纬度上的拓展，同时向量化表示了。对于每一个数据样本，其到超平面都有一个距离，其中，支持向量的距离最小。SVM的目标，就是找到这样一个超平面，使得支持向量到它的距离最大。也就是说，使得最小的距离都最大，那么与其他点的距离就更大了。
2.3 模型建立
对于每一个数据点，令其到超平面的数据为 
，我们的如果我们将支持向量到超平面的距离令为
，那么，显然 
，其中m为样本数量。因此我们可以建立如下的模型：
这个模型是没法求解的，因此我们需要在这个基础上重写。
约束条件两边同时除以得到
如果我们令
，就有
也就是说，对于以前的
，我们对其进行了一个放缩，得到了
，其中放缩因子为 
。由于是等比例放缩，这样做不会影响结果。那么，为什么要这样做呢？首先，为了表示方便，我们重新用 来表示 ，因此上面的公式可以写为如下形式：
而此时的超平面是。显然，我们就获得了一系列与超平面平行的超平面！而其中 
和 
是经过支持向量的两个超平面！，具体可以见下图：
此时，支持向量到超平面的距离同样可以表示为，并且在这种情况下，
，所以距离进一步表示为
。SVM的目标是该距离最大，等价于
最小。因此，我们的目标函数就确定了。当然，不可能无限小，必须还要满足一定的约束条件，根据上图可知，所有数据点必须在 和 的外侧，也就是必须满足
我们将这两个不等式合并起来：
这样，我们就可以将SVM的模型表示为：
这里将目标函数写为
只是为了求解方便。至此，模型建立完毕。
2.4 模型求解
显然，上面的模型是一个带有不等式约束的非线性优化模型，令 
,利用我们之前提到的KKT条件，先定义拉格朗日函数：
引入KKT条件：
现在我们来研究一下这个拉格朗日函数：
因此在约束条件满足的情况下，
等价于
。由于
满足我们前置知识二提到的两个条件，我们可以将转化为
。为什么满足？可以移步：https://blog.csdn.net/xianlingmao/article/details/7919597。不感兴趣就算了，实在有点烧脑。
好了，现在目标变为了求。为什么要做这一步转换？因为里面的
很好求。我们对 
和b求偏导，并令其等于0，可得：
其中，上标(j)代表的是第j个特征，将求得的结果代入
后有：
因此现在变为了求
![\underset{\lambda}{max}[\sum_{j=1}^{m}\lambda_{i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\lambda_{i}\lambda_{j}x_{i}x_{j}y_{i}y_{j}]](http://img.e-com-net.com/image/info8/602298d9083844d2a0775db8fcc96018.gif)
2.5 SMO算法
smo叫做序列最小优化，所谓“序列”，就是一个一个求。其核心思想是固定一部分变量，来求解剩下的变量的最优解。在，变量是m个 
，由于约束
的存在，我们一次最多固定m-2个变量，即一次最少要求解两个变量的最优解。假设求解的这两个变量为 
令
,则有
，从而
，这样我们就将其中一个变量用另一个变量表示出来。此时，我们就转化成了只有一个变量
，以及一个约束的优化问题。对该问题求解，求到的代入原目标中，即，然后再次这样求解。重复多次直到满足停止条件。显然，这种算法不能求到真正的最优解，只能求出一个满意解。
SMO算法结束后，我们求得了满足要求的
，接下来的目标是求 b。由于支持向量满足等式，我们将和支持向量的数据代入后即可求得b。如果存在多个支持向量，那么最好对由每个支持向量求出来的b取一个平均值。
事实上，这只是SMO算法的一个简化版本，更为详细的计算过程我将在下一篇文章中讲解。
三、软间隔
3.1 定义
软间隔与硬间隔对应，它指的是样本不能够线性可分，此时我们的处理方式是允许一部分数据出现在间隔带里，如下图所示：
3.2 模型建立
硬间隔情况下，我们要求所有数据严格满足约束 
。软间隔情况下，我们会对这个约束相应放宽，改为
，
反映了在图上是超出间隔带的距离，如下图所示：
相应的，目标函数也发生了变化：
，其中，C反映了我们对不满足约束的样本的容忍程度，C=0即容忍度为零。
3.3 模型求解
构造拉格朗日函数：
同样的，转化为对偶形式：
，令里面的
分别对
的偏导数等于0，有：
回代：
，因此目标函数没有发生变化，但是外层的的约束条件发生了变化：
然后再用SMO算法求即可。
最后在根据支持向量求b的时候要注意一个问题，位于间隔带内部的数据点算不算支持向量？这时就要提出支持向量更广义的概念，所谓“支持”，就是会帮助构造超平面，从这个意义上来说，位于间隔带内部的数据点也算支持向量，因此也要用这些数据求b。
四、非线性SVM与核函数
对于如下图所示的在一定维度下非线性可分的数据集：
我们的处理方式是映射到更高维的空间，然后用一个维数更高的超平面分割它们：
用 
表示经过映射后得到的新向量，那么最终的目标函数就变为了![\underset{\lambda}{max}[\sum_{j=1}^{m}\lambda_{i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\lambda_{i}\lambda_{j}\Phi(x_{i})\Phi(x_{j})y_{i}y_{j}]](http://img.e-com-net.com/image/info8/99474bd7ff7b4f499258a4f6961ec6bc.gif)
。 然而，将样本映射到高维空间后，特征会变得非常多，那么
的计算量将会非常大。不过，好在我们最终需要的只是的计算结果，而不需要考虑其计算过程。如果有这样一个函数
，那么我们就不需要将映射后的特征挨个挨个计算。并且，理论证明这样的函数是存在的，这种函数就叫做核函数。常见的核函数有：
线性核函数：
多项式核函数：
高斯核函数：
每一个核函数，都对应着一种映射，可以通过该核函数求出映射后的向量的内积，因此我们只需要使用核函数就可以了。