opencv相机校准和3D重建代码部分

一、相机标定： 

先了解以下函数的含义以及作用：

一、zeros()

返回来一个给定形状和类型的用0填充的数组；
zeros(shape, dtype=float, order=‘C’)
shape:形状
dtype:数据类型，可选参数，默认numpy.float64
order:可选参数，c代表与c语言类似，行优先；F代表列优先

例如：

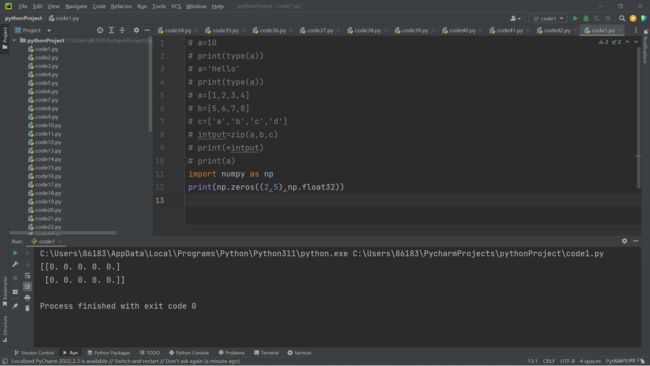
print(np.zeros((2,5),dtype= np.int))

输出： 

二、reshape()

reshape()函数的功能是改变数组或矩阵的形状

a.reshape(m,n)表示将原有数组a转化为一个m行n列的新数组，a自身不变。m与n的乘积等于数组中的元素总数。

reshape(m,n)中参数m或n其中一个可写为"-1"，"-1"的作用在于计算机根据原数组中的元素总数自动计算行或列的值。

列如，其中a的值没有发生改变，除非给a重新赋值

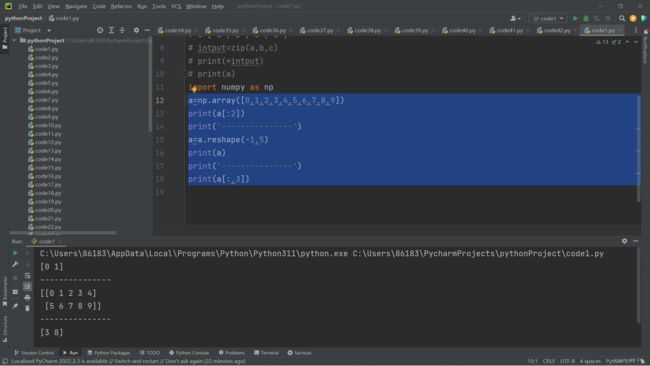
a=np.array([0,1,2,3,4,5,6,7,8,9])
print(a.reshape(-1,5))
print(a)

输出： 

三、python的切片操作

[:i]：这是切片操作，在下标 i (左闭右开)之前的元素都保留,适用于Python中的list(也就是数组)，也适用于numpy科学结构(array等)。 

[:,i] ：这也是切片操作，不同的是：保留第一个维度所有元素，第二维度元素保留到i；只适用numpy的科学数据结构。

更通俗易懂的是：

X[:,1] 就是取所有行的第1列的元素。
X[:,m:n]即取矩阵X的所有行中的的第m到n-1列数据
X[0,:]就是取矩阵X的第0行的所有元素，X[1,:]取矩阵X的第一行的所有元素。

列如：

a=np.array([0,1,2,3,4,5,6,7,8,9])
print(a[:2])
print('---------------')
a=a.reshape(-1,5)
print(a)
print('---------------')
print(a[:,3])

 输出：

四、mgrid[]

np.mgrid[start:end:step] ，start:开始坐标，stop:结束坐标（实数不包括，复数包括），step:步长

返回多维结构，常见的如2D图形，3D图形。

五、glob

glob是实用的文件名匹配库，glob.glob()函数将会匹配给定路径下的所有pattern，并以列表形式返回。

用它可以查找符合特定规则的文件路径名。查找文件只用到三个匹配符：

”*”, 匹配 0 个或多个字符；
“?”, ”?”匹配单个字符；
“[]”：”[]”匹配指定范围内的字符，如：[0-9]匹配数字；

 注意：如果文件名以“点”开头 ，无法被 '*' 和 '?'匹配，如：".card.gif"

glob模块的主要方法就是glob,该方法返回所有匹配的文件路径列表（list）；

该方法需要一个参数用来指定匹配的路径字符串（字符串可以为绝对路径也可以为相对路径），其返回的文件名只包括当前目录里的文件名，不包括子文件夹里的文件。

注意：在Windows操作系统下，模式M*可以匹配名称以m和M开头的所有文件，因为文件名称和文件名称通配是不区分大小写的。在大多数其他操作系统上，通配是区分大小写的。

六、findChessboardCorners()

在双目视觉应用领域，要想进行精确的操作，第一步要做的就是对摄像机的内参数进行求解，这个过程称之为标定。整个标定过程由cameraCalibrate()函数完成(下面会讲到)，测量相机焦距和便宜主要的原理是张正友标定法，测量畸变参数是Brown算法。该标定函数的一个输入参数是像点坐标，即在摄像机成像平面上对应角点相对于摄像机坐标系的二维坐标（像素点）。而获得像点坐标的函数第一步就是找到角点坐标，函数是findChessboardCorners()

功能：找到标定板内角点位置（标定板是专用器具，需要有严格的规格控制，标定板的制作精度直接影响标定精度；角点是指黑白色相接的方块定点部分；内角点是不与标定板边缘接触的内部角点）
参数：1.输入的图像矩阵，必须是8-bit灰度图或者彩色图像，在图像传入函数之前，一般经过灰度处理，还有滤波操作。
　　　2.内角点的size，表示方式是定义Size PatSize(m,n)，将PatSize作为参数传入。这里是内角点的行列数，不包括边缘角点行列数；行数和列数不要相同，这样的话函数会辨别出标定板的方向，如果行列数相同，那么函数每次画出来的角点起始位置会变化，不利于标定。棋盘上每一排和每一列的内角数。w=棋盘板一行上黑白块的数量-1，h=棋盘板一列上黑白块的数量-1，例如：10x6的棋盘板，则(w,h)=(9,5)

总结：该函数的功能就是判断图像内是否包含完整的棋盘图，如果能够检测完全，就把他们的角点坐标按 顺序（逐行，从左到右）记录下来，并返回非0数，否则返回0。 这里对size参数要求非常严格，函数必须检测到相同的size才会返回非0，否则返回0，这里一定要注意。角点检测不完全时，可能画不出图像，或者画出红色角点；正确的图像后面有参考。

七、cornerSubPix()

提取到的角点只能达到像素级别，在很多情况下并不能满足实际的需求，这时，我们则需要使用cornerSubPix()对检测到的角点作进一步的优化计算，可使角点的精度达到亚像素级别。

第一个参数是输入图像，和findChessboardCorners()中的输入图像是同一个图像。
第二个参数是检测到的角点，即是输入也是输出。

第三个参数是计算亚像素角点时考虑的区域的大小，大小为NXN; N=(winSize*2+1)。

第四个参数作用类似于winSize，但是总是具有较小的范围，通常忽略（即Size(-1, -1)）。

第五个参数用于表示计算亚像素时停止迭代的标准，可选的值有cv::TermCriteria::MAX_ITER 、cv::TermCriteria::EPS（可以是两者其一，或两者均选），前者表示迭代次数达到了最大次数时停止，后者表示角点位置变化的最小值已经达到最小时停止迭代。二者均使用cv::TermCriteria()构造函数进行指定。

八、drawChessboardCorners（）棋盘格角点的绘制

参数：

棋盘格图像（8UC3）即是输入也是输出
棋盘格内部角点的行、列数
findChessboardCorners()输出的角点

findChessboardCorners()的返回值

import numpy as np
import cv2 as cv
import glob
# 终止条件
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 30, 0.001)
# 准备对象点， 如 (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((6*7,3), np.float32)
objp[:,:2] = np.mgrid[0:7,0:6].T.reshape(-1,2)
# 用于存储所有图像的对象点和图像点的数组。
objpoints = [] # 真实世界中的3d点
imgpoints = [] # 图像中的2d点
images = glob.glob('*.jpg')
for fname in images:
    img = cv.imread(fname)
    gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
    # 找到棋盘角落
    ret, corners = cv.findChessboardCorners(gray, (7,6), None)
    # 如果找到，添加对象点，图像点（细化之后）
    if ret == True:
        objpoints.append(objp)
        corners2 = cv.cornerSubPix(gray,corners, (11,11), (-1,-1), criteria)
        imgpoints.append(corners)
        # 绘制并显示拐角
        cv.drawChessboardCorners(img, (7,6), corners2, ret)
        cv.imshow('img', img)
        cv.waitKey(500)
cv.destroyAllWindows()

在OpenCV中，可以使用calibrateCamera函数，通过多个视角的2D/3D对应，求解出该相机的内参数和每一个视角的外参数。

相机标定的目的是：建立相机成像几何模型并矫正透视畸变。

建立相机几何成像模型：计算机视觉的首要任务就是要通过拍摄到的图像信息获取到物体在真实三维世界里相对应的信息，于是，建立物体从三维世界映射到相机成像平面这一过程中的几何模型就显得尤为重要，而这一过程最关键的部分就是要得到相机的内参和外参。

矫正透镜畸变:由于透镜的制造工艺,会使成像产生多种形式的畸变，于是为了去除畸变（使成像后的图像与真实世界的景象保持一致)，人们计算并利用畸变系数来矫正这种像差。

ret, mtx, dist, rvecs, tvecs = cv.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)

参数介绍：

objectPoints为世界坐标系中的点；

imagePoints为其对应的图像坐标系中的点（像素坐标）。

imageSize为图像的大小，在计算相机的内参数和畸变矩阵需要用到；

返回：

cameraMatrix为内参数矩阵；

distCoeffs为畸变矩阵；

rvecs为旋转向量；

tvecs为位移向量；

二、畸形矫正

我们可以拍摄图像并对其进行扭曲。OpenCV提供了两种方法来执行此操作。但是，首先，我们可以使用cv.getOptimalNewCameraMatrix()基于自由缩放参数来优化相机矩阵，根据比例因子返回相应的新的相机内参矩阵。如果缩放参数alpha = 0，则返回具有最少不需要像素的未失真图像。因此，它甚至可能会删除图像角落的一些像素。如果alpha = 1，则所有像素都保留有一些额外的黑色图像。此函数还返回可用于裁剪结果的图像ROI。

因此，我们拍摄一张新图像

img = cv.imread('left12.jpg')
h,  w = img.shape[:2]
newcameramtx, roi = cv.getOptimalNewCameraMatrix(mtx, dist, (w,h), 1, (w,h))

参数：

cameraMatrix 相机内参矩阵；
distCoeffs 相机畸变参数；
imageSize 图像尺寸；
alpha  缩放比例（当alpha=1时，所有像素均保留，但存在黑色边框。 //当alpha=0时，损              最多的像素，没有黑色边框）
newImgSize = Size() 校正后的图像尺寸

方法一：使用 undistort（）

函数功能：直接对图像进行畸变矫正，这是最简单的方法。只需调用该函数并使用上面获得的ROI裁剪结果即可。

其内部调用了initUndistortRectifyMap和remap函数。

dst = cv.undistort(img, mtx, dist, None, newcameramtx)
# 剪裁图像
x, y, w, h = roi
dst = dst[y:y+h, x:x+w]
cv.imwrite('calibresult.png', dst)

参数：

src 原始图像
cameraMatrix 原相机内参矩阵
distCoeffs  相机畸变参数
newCameraMatrix  新相机内参矩阵

方法二：initUndistortRectifyMap()用于计算原始图像和矫正图像之间的转换关系，将结果以映射的形式表达，映射关系存储在map1和map2中，remap()把原始图像中某位置的像素映射到矫正后的图像指定位置。

# undistort
mapx, mapy = cv.initUndistortRectifyMap(mtx, dist, None, newcameramtx, (w,h), 5)
dst = cv.remap(img, mapx, mapy, cv.INTER_LINEAR)
# 裁剪图像
x, y, w, h = roi
dst = dst[y:y+h, x:x+w]
cv.imwrite('calibresult.png', dst)

initUndistortRectifyMap() 参数：

cameraMatrix 原相机内参矩阵
distCoeffs 相机畸变参数
R 可选的修正变换矩阵 
newCameraMatrix 新相机内参矩阵
size 去畸变后图像的尺寸
map1 第一个输出映射
map2  第二个输出映射

remp()参数：

src 矫正图像         
map1 第一个映射          
map2 第二个映射      
interpolation 插值方式
注意：如果有多个图片需要矫正，那么推荐使用法二。
因为initUndistortRectifyMap() 只需计算一次即可，不需要每次循环都计算，因此可以将initUndistortRectifyMap() 放在循环外面。而法二undistort()函数内部调用了initUndistortRectifyMap和remap，所以每张图像都计算1次initUndistortRectifyMap，这会大大降低效率，增加程序耗时。

重投影误差

重投影误差可以很好地估计找到的参数的精确程度。重投影误差越接近零，我们发现的参数越准确。给定固有，失真，旋转和平移矩阵，我们必须首先使用cv.projectPoints()将对象点转换为图像点。然后，我们可以计算出通过变换得到的绝对值和拐角发现算法之间的绝对值范数。为了找到平均误差，我们计算为所有校准图像计算的误差的算术平均值。

mean_error = 0
for i in xrange(len(objpoints)):
    imgpoints2, _ = cv.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
    error = cv.norm(imgpoints[i], imgpoints2, cv.NORM_L2)/len(imgpoints2)
    mean_error += error
print( "total error: {}".format(mean_error/len(objpoints)) )

 projectPoints():用来计算三维点投射到像素坐标系的二维点

参数：

世界坐标系3D三维坐标

世界坐标系换到相机坐标系的旋转向量

世界坐标系换到相机坐标系的平移向量

相机的内参矩阵

相机的畸变系数矩阵