2022数模国赛C题思路详解-古代玻璃制品的成分分析与鉴别

 

完整作品（含代码/文献/数据集/分类答案 ）：正在为您运送作品详情

题目定位：数据分析题（数据量少，维度较多）

参考往年题目：2021年国赛B题

一、题目背景分析

这几段主要是交代题目的背景，讲解了古代玻璃制品的特征，解释了其化学成分含量的差异性是鉴别分类的重要因素。同时也引出了“风化”现象对玻璃制品成分变化的影响，并举例说明。

这里我们结合题目不难看出，该题主要就是要求我们通过化学成分的分析探索出“风化”对玻璃中化学成分含量变化的影响，并希望我们可以提出一种分析鉴别方案可以排除“风化”带来的这种影响。

题目背景中理解起来还是蛮简单的，但是不要忽略条件，题目中给出的助熔剂、稳定剂以及一些含量高的化学成分都有可能是我们后续分析的重要支撑。

这里题目里给出已有明确的两种类型分类，这很容易让我们想到机器学习和0-1分类，这些分类信息则可以相当于为训练集与测试集。

同时注意题目里强调的【有效数据】说明，需要对缺失值和空值进行预处理。

注：题目中背景补充部分较多，要注意最后分析的时候要结合这些背景知识，不能全部忽略。

二、逐题题目分析

（1）对这些玻璃文物的〔表面风化〕与〔其玻璃类型、纹饰和颜色〕的关系进行分析

对应的数据为表单一，这里可以简单地把文物按是否风化分成两类，然后分别统计三个指标的频率。也可以利用交叉列联表、相关性分析等等传统的统计学方法。

除了基础的分析外最好辅以直观的可视化图表 ，这里建议大家尝试气泡图等多维数据图。

分析完后需要得出结论，即找出风化/无风化的特征倾向，比如风化的文物颜色更可能变浅，为之后的〔风化对化学成分含量影响以及分类判别方案〕提供支撑。

注:数据中存在缺失值

（2）结合玻璃的类型，分析文物样品表面有无风化化学成分含量的统计规律

这里出现了一句读起来有些别扭的话“分析文物样品表面有无风化化学成分含量的统计规律”，笔者认为题目的意思是让我们把文物样品表面按有无风化分成两类，对比统计<风化>和<无风化>两种状态下文物样品化学成分含量的统计规律。

玻璃的类型只有两类即高钾和铅钡，我们分别记为0和1。

这里涉及表单2，需要我们利用表单一对应编号的分类给表单二的数据贴上0/1标签。

同时要注意，表单二中有些文物对应多点的数据，不能直接复制粘贴表单一的分类数据列。

与（1）小问一样，题目都要求我们对统计规律进行分析，最简单的思路就是把总数据按有无风化和类型分成四类，即<高钾无风化>，<高钾风化>，<铅钡无风化>，<铅钡风化>，然后对四类的数据分别进行统计分析。也可以先对数据进行聚类，然后与人为划分的四种类别进行对比。

统计分析方法思路:

☞列基础统计量表格，各化学成分含量的平均值、方差、变异系数、中位数、极差。

☞箱线图（同时可实现异常值的剔除）统计各化学成分数据值分布特征

☞回归拟合:尝试将不同化学成分含量做为自变量，类型（4种）设为y，进行多变量拟合。

☞利用不同元素的含量（元素守恒）构建新的特征指标，比如两种化学成分的比值，或者几种化学成分的求和，设为新指标，去试验是否存在指向性的风化指标。

可视化:折线图饼图散点图好像都OK，个人觉得高维散点图会直观一点。可视化需要突出同一类型风化前后各化学成分的变化趋势。

结论:最终应该得到两种类型的玻璃各自化学成分含量受风化的影响是怎样的。

注:题目里曾提到化学成分总和85-105%方可视为有效数据，所以需要提前对数据进行检验，剔除无效数据。

（3）并根据风化点检测数据，预测其风化前的化学成分含量

第（2）问我们得出了风化对化学成分含量的影响，第（3）问我们需要根据得到的影响结论反推未知成分含量。这就需要我们具体地量化风化的影响程度，构建相应方程。

笔者最先想到的就是机器学习中的逻辑回归，但是题目数据量太少，缺失数据也较多，机器学习根本训练不起来，但是机器学习的思想我们还是可以用的。

预测思路:

设风化程度为 f ，风化后各化学成分含量为x'i，其改变量为△xi，各风化程度对应的化学成分改变规律为方程Q。

首先量化风化的程度（利用表单一的特征分析），根据不同的玻璃表面特性判断出风化的程度（可人为设定风化的等级1/2/3/4……无风化则为0）

然后量化出不同程度风化对应的各化学成分对应改变程度（利用表单二的风化对化学成分影响，影响程度与风化程度一一对应）即方程Q。

f ，x'i 代入Q求出xi。

具体量化方法:

☞逻辑回归:利用已知的数据建立逻辑回归方程并拟合出预测方程。（根据2结论检验）

☞支持向量机

☞k均值聚类

（1）亚类划分

首先要统计出两个类别的统计规律，此时不再考虑风化与否。

统计方法与问题一相似，此处的亚类划分用聚类方法为宜，也可采用主成分分析+层次划分/topsis熵权法综合评价模型。觉得篇幅不够可以辅用系谱图，分支树或者采用决策树和随机森林等方法。需要结合题中的背景信息并查阅文献对划分结果进行详细分析。

（2）合理性敏感性分析

合理性分析角度:多种方法分类结果一致/符合客观事实

敏感性分析角度:改变聚类（或者其他模型的）参数对结果的影响/给原始数据加小幅度噪声获得新的划分结果与原结果对比

敏感性分析一定要有图表说明!一般折线图即可（参考美赛）

利用问题2的方法，直接利用原始数据对大类进行划分，找出分类模型。然后反代问题3数据即可得出。

敏感性分析同上。

最后一问要扣背景知识，〔关联关系〕可以采用多变量列联表、交叉分析表、皮尔逊相关系数计算、卡方分析等方法。

结合参考文献，构建新的特征指标（各化学成分指标加减乘除等等）。一般关联关系为:成分A随着成分B的增加而增加，成分C和成分D比值恒定，成分E和成分F互补等。

这一问比较开放，没有什么传统的模型可以直接拿来套，笔者觉得可以采用熵权法的思想，针对不同变量两两之间进行分析，从而判断两种变量的变化是否存在联系。

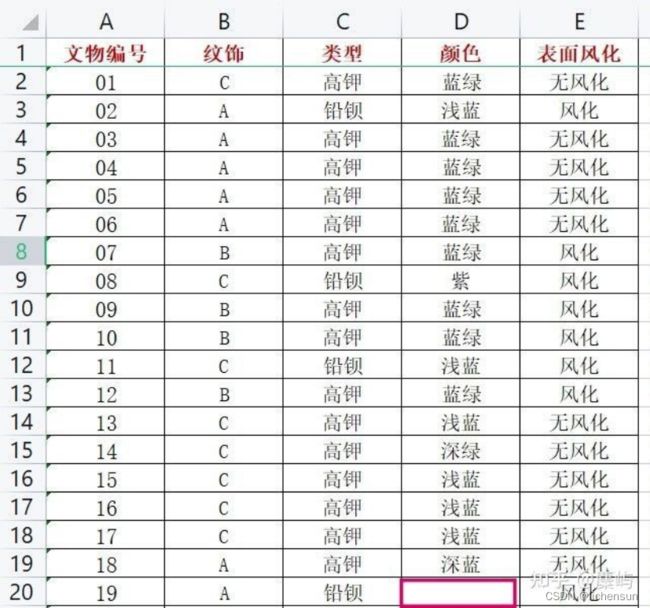
三、数据集分析

数据量很少，变量较多，对数据进行预处理是比较简单的，主要做一些异常值分析和分类标签，以及每条数据的有效性检验即可。