f分布表完整图a=0.01_Matlab中的数据分析之概率分布与检验实例讲解
频数表和直方图
一组数据(样本)往往是杂乱无章的,做出它的频数表和直方图,可以看作是对这组数据的一个初步整理和直观描述。
将数据的取值范围划分为若干个区间,然后统计这组数据在每个区间中出现的次数,称为频数,由此得到一个频数表。以数据的取值为横坐标,频数为纵坐标,画出一个阶梯形的图,称为直方图,或频数分布图。
若样本容量不大,能够手工做出频数表和直方图,当样本容量较大时则可以借助Matlab 软件。让我们以下面的例子为例,介绍频数表和直方图的作法。
【例1】 学生的身高和体重
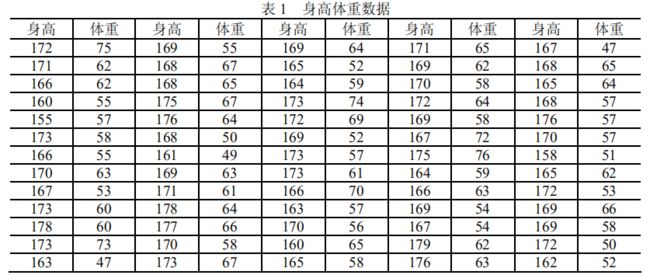
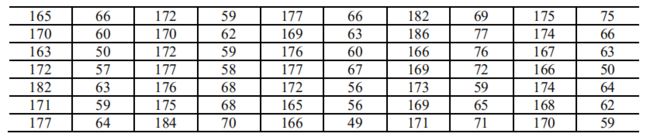
(i) 数据输入
数据输入通常有两种方法,一种是在交互环境中直接输入,如果在统计中数据量比较大,这样作不太方便;另一种办法是先把数据写入一个纯文本数据文件data.txt 中,格式如例 1 的表 1,有 20 行、10 列,数据列之间用空格键或 Tab 键分割,该数据文件 data.txt 存放在 matlab\work 子目录下,在 Matlab 中用 load 命令读入数据,具体作法是:
load data.txt
这样在内存中建立了一个变量 data,它是一个包含有20×10 个数据的矩阵。
为了得到我们需要的 100 个身高和体重各为一列的矩阵,应做如下的改变:
high=data(:,1:2:9);high=high(:) weight=data(:,2:2:10);weight=weight(:)
(ii)作频数表及直方图
求频数用hist 命令实现,其用法是:
[N,X] = hist(Y,M)
得到数组(行、列均可)Y 的频数表。它将区间[min(Y),max(Y)]等分为 M 份(缺省时M 设定为10),N 返回M 个小区间的频数,X 返回M 个小区间的中点。
命令
hist(Y,M)
画出数组Y 的直方图。
对于例1 的数据,编写程序如下:
向上滑动阅览
load data.txt;
high=data(:,1:2:9);high=high(:);
weight=data(:,2:2:10);weight=weight(:);
[n1,x1]=hist(high)
%下面语句与hist命令等价
%n1=[length(find(high<158.1)),...
% length(find(high>=158.1&high<161.2)),...
% length(find(high>=161.2&high<164.5)),...
% length(find(high>=164.5&high<167.6)),...
% length(find(high>=167.6&high<170.7)),...
% length(find(high>=170.7&high<173.8)),...
% length(find(high>=173.8&high<176.9)),...
% length(find(high>=176.9&high<180)),...
% length(find(high>=180&high<183.1)),...
% length(find(high>=183.1))]
[n2,x2]=hist(weight)
subplot(1,2,1), hist(high)
subplot(1,2,2), hist(weight)
计算结果略,直方图如图 1 所示。
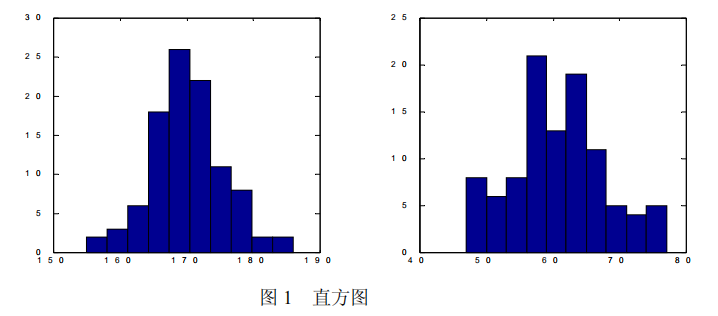
从直方图上可以看出,身高的分布大致呈中间高、两端低的钟形;而体重则看不出什么规律。要想从数值上给出更确切的描述,需要进一步研究反映数据特征的所谓“统 计量”。直方图所展示的身高的分布形状可看作正态分布,当然也可以用这组数据对分布作假设检验。
【例2】
统计下列五行字符串中字符 a、g、c、t 出现的频数
1.aggcacggaaaaacgggaataacggaggaggacttggcacggcattacacggagg
2.cggaggacaaacgggatggcggtattggaggtggcggactgttcgggga
3.gggacggatacggattctggccacggacggaaaggaggacacggcggacataca
4.atggataacggaaacaaaccagacaaacttcggtagaaatacagaagctta
5.cggctggcggacaacggactggcggattccaaaaacggaggaggcggacggaggc
解
把上述五行复制到一个纯文本数据文件 shuju.txt 中,放在 matlab\work 子目录下,编写如下程序:
向上滑动阅览
clc
fid1=fopen('shuju.txt','r');
i=1;
while (~feof(fid1))
data=fgetl(fid1); a=length(find(data==97));
b=length(find(data==99));
c=length(find(data==103));
d=length(find(data==116));
e=length(find(data>=97&data<=122));
f(i,:)=[a b c d e a+b+c+d];
i=i+1;
end
f, he=sum(f)
dlmwrite('pinshu.txt',f); dlmwrite('pinshu.txt',he,'-append');
fclose(fid1);
我们把统计结果最后写到一个纯文本文件 pinshu.txt 中,在程序中多引进了几个变量,是为了检验字符串是否只包含 a、g、c、t 四个字符。
Matlab 统计工具箱(Toolbox\Stats)中的概率分布
Matlab 统计工具箱中有 27 种概率分布,这里只对常见的 4 种分布列出命令的字符:
norm 正态分布;
chi2 χ2分布;
t t 分布;
f F分布
工具箱对每一种分布都提供 5 类函数,其命令的字符是:
pdf 概率密度;
cdf 分布函数;
inv 分布函数的反函数;
stat 均值与方差;
rnd 随机数生成
当需要一种分布的某一类函数时,将以上所列的分布命令字符与函数命令字符接起来,并输入自变量(可以是标量、数组或矩阵)和参数就行了。
如:p=normpdf(x,mu,sigma) 均值 mu、标准差 sigma 的正态分布在 x 的密度函数 (mu=0,sigma=1 时可缺省)。p=tcdf(x,n) t 分布(自由度 n)在 x 的分布函数。
x=chi2inv(p,n) χ2 分布(自由度 n)使分布函数 F(x)=p 的 x(即 p 分位数)。
[m,v]=fstat(n1,n2) F分布(自由度 n1,n2)的均值 m 和方差 v。
几个分布的密度函数图形就可以用这些命令作出,如
x=-6:0.01:6;y=normpdf(x);z=normpdf(x,0,2);
plot(x,y,x,z),gtext('N(0,1)'),gtext('N(0,2^2)')
分布函数的反函数的意义从下例看出:
x=chi2inv(0.9,10)
x =
15.9872
如果反过来计算,则
P=chi2cdf(15.9872,10)
P =
0.9000
Matlab 统计工具箱中,有专门计算总体均值、标准差的点估计和区间估计的函数。
对于正态总体,命令是 [mu,sigma,muci,sigmaci]=normfit(x,alpha)
其中 x 为样本(数组或矩阵),alpha 为显著性水平α (alpha 缺省时设定为 0.05),返回总体均值 μ 和标准差σ 的点估计 mu 和 sigma,及总体均值 μ 和标准差σ 的区间估计 muci 和 sigmaci。当 x 为矩阵时,x 的每一列作为一个样本。
Matlab 统计工具箱中还提供了一些具有特定分布总体的区间估计的命令,如 expfit,poissfit,gamfit,具体用法参见帮助系统。
在 Matlab 中 Z 检验法由函数 ztest 来实现,命令为 [h,p,ci]=ztest(x,mu,sigma,alpha,tail)
其中输入参数 x 是样本,mu 是 H0 中的 μ0 ,sigma 是总体标准差σ ,alpha 是显著性 水平α (alpha 缺省时设定为 0.05),tail 是对备选假设 H1 的选择:H1 为 μ ≠ μ0 时 用 tail=0(可缺省);H1 为 μ > μ0时用 tail=1;H1 为 μ < μ0 时用 tail=-1。输出参 数 h=0 表示接受 H0 ,h=1 表示拒绝 H0 ,p 表示在假设 H0 下样本均值出现的概率,p 越小 H0越值得怀疑,ci 是 μ0 的置信区间。
【例 3】
某车间用一台包装机包装糖果。包得的袋装糖重是一个随机变量,它服从正态分布。当机器正常时,其均值为 0.5 公斤,标准差为 0.015 公斤。某日开工后为检验 包装机是否正常,随机地抽取它所包装的糖 9 袋,称得净重为(公斤):
0.497 0.506 0.518 0.524 0.498 0.511 0.520 0.515 0.512
问机器是否正常?
解
总体σ 已知, x~N ( μ ,0.0152 ) ,μ 未知。于是提出假设 H0 : μ = μ0 = 0.5和 H1:μ ≠:0.5 。
Matlab 实现如下
x=[0.497 0.506 0.518 0.524 0.498... 0.511 0.520 0.515 0.512];
[h,p,ci]=ztest(x,0.5,0.015)
求得 h=1,p=0.0248,说明在 0.05 的水平下,可拒绝原假设,即认为这天包装机工作不正常。
σ2 未知,关于 μ 的检验(t 检验)
在 Matlab中t 检验法由函数 ttest 来实现,命令为
[h,p,ci]=ttest(x,mu,alpha,tail)
【例 4】
某种电子元件的寿命 x (以小时计)服从正态分布, 2 μ,σ 均未知.现得 16 只 元件的寿命如下:
159 280 101 212 224 379 179 264
222 362 168 250 149 260 485 170
问是否有理由认为元件的平均寿命大于 225(小时)?
解
按题意需检验
H0 : μ ≤ μ0 = 225, H1 : μ > 225,
取α = 0.05。
Matlab 实现如下:
x=[159 280 101 212 224 379 179 264 ...
222 362 168 250 149 260 485 170]; [h,p,ci]=ttest(x,225,0.05,1)
求得 h=0,p=0.2570,说明在显著水平为 0.05 的情况下,不能拒绝原假设,认为元件的平均寿命不大于 225 小时。
两个正态总体均值差的检验(t 检验)
还可以用t 检验法检验具有相同方差的 2 个正态总体均值差的假设。在 Matlab 中 由函数 ttest2 实现,命令为:
[h,p,ci]=ttest2(x,y,alpha,tail)
与上面的 ttest 相比,不同处只在于输入的是两个样本 x,y(长度不一定相同), 而不是一个样本和它的总体均值;tail 的用法与 ttest 相似,可参看帮助系统。
【例 5】
在平炉上进行一项试验以确定改变操作方法的建议是否会增加钢的得率,试验是在同一平炉上进行的。每炼一炉钢时除操作方法外,其它条件都可能做到相同。先用标准方法炼一炉,然后用建议的新方法炼一炉,以后交换进行,各炼了 10 炉,其得率分别为
(1)标准方法 78.1 72.4 76.2 74.3 77.4 78.4 76.0 75.6 76.7 77.3
(2)新方法 79.1 81.0 77.3 79.1 80.0 79.1 79.1 77.3 80.2 82.1
设这两个样本相互独立且分别来自正态总体N(μ1,σ2),N(μ2,σ2) ,μ1,μ2,σ2均未知,问建议的新方法能否提高得率?(取α = 0.05 。)
解
(1)需要检验假设
H0 : μ1 − μ2 ≥ 0 ,
H1: μ1 − μ2 < 0.
(2)Matlab 实现
x=[78.1 72.4 76.2 74.3 77.4 78.4 76.0 75.6 76.7 77.3]; y=[79.1 81.0 77.3 79.1 80.0 79.1 79.1 77.3 80.2 82.1]; [h,p,ci]=ttest2(x,y,0.05,-1)
求得 h=1,p=2.2126×10-4。表明在α = 0.05 的显著水平下,可以拒绝原假设,即认为建议的新操作方法较原方法优。
• END •
模友们可能已经发现:现在公众号推送文章的顺序,已经不会按时间排列了。这种变化,可能会让各位模友错过我们每天的推送。
所以,如果你还想像往常一样,聚焦数模乐园,就需要将“数模乐园”标为星标公众号,同时在阅读完文章后,别忘了给一个“在看”哦。
星标步骤
(1)点击页面最上方“数模乐园”,进入公众号主页
(2)点击右上角的小点点,在弹出页面点击“设为星标”,就可以啦。


扫码关注我们

2020国际赛QQ参赛群


球分享

球点赞

球在看