压缩感知与稀疏恢复 matlab示例(附代码)
前言
最近因为科研需要,又开始重新研究压缩感知(CS)与稀疏恢复(SR)理论。本人系初学,很多东西都没有学明白,姑且先摸着石头过河,仿照网上的例子,用matlab编程实现最基本的例子,写下了这篇笔记。
原理
关于压缩感知与稀疏恢复的原理就不再赘述,网上有很多博主写的很详细,这里推荐https://zhuanlan.zhihu.com/p/22445302
这篇文章原理写的通俗易懂。本文在这篇文章的基础上结合https://blog.csdn.net/xiahouzuoxin/article/details/38820925所给出的代码,形成了我自己的理解。
信号模型
这里选择比较简单的信号形式:一些单音正弦信号叠加。选取两个单音正弦信号,频率为10Hz和15Hz,幅度分别为1.5V和1V,当然这些参数在代码中都是可调的。两个信号时域图如下所示:
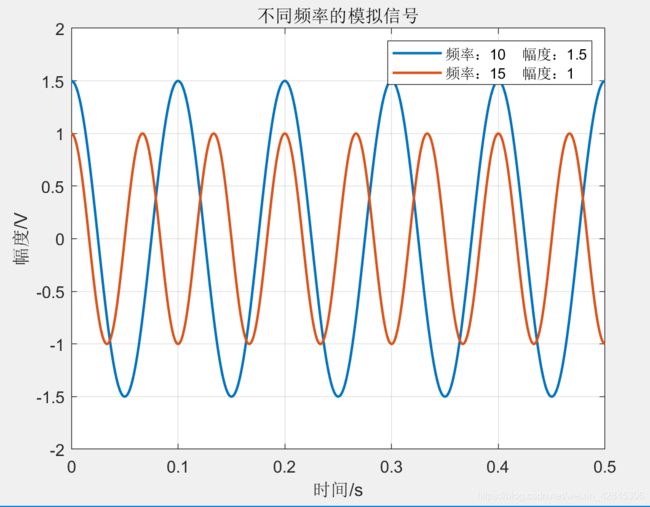
叠加后时域图如下:
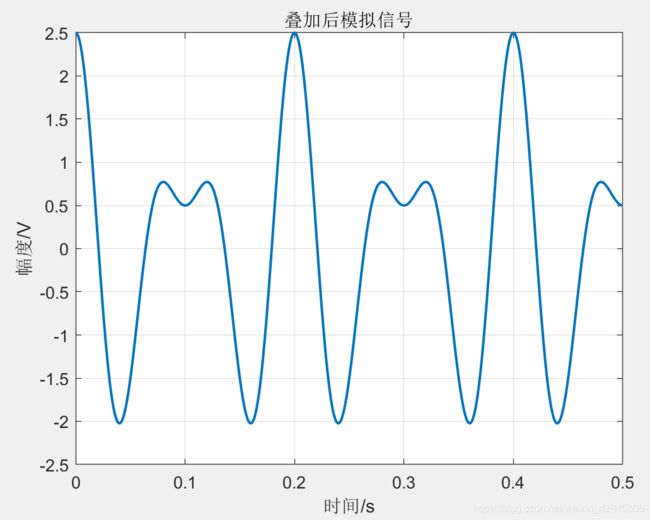
信号的最大频率为15Hz,根据奈奎斯特采样定理,最小采样速率为两倍最大频率,即N_fs=30Hz。事实上,计算机中无法处理模拟信号,上面两张图是用非常高的采样速率(3kHz)得到的,因此看起来像是模拟信号。
为了减少计算机的工作量,将采样速率降低为fs=600Hz,采样时宽为T=5s。信号采样结果如下所示(时间截断到1s)。和上图相比,看起来没什么信息损失。
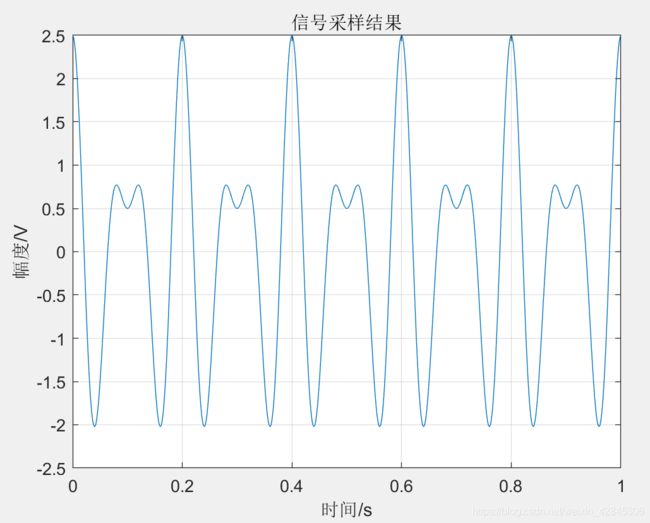
用fft加fftshift的方法(不知道的可以翻我的matlab专栏关于画频谱的),绘制该信号的双边频谱如下图所示(只显示100Hz以内)。

可以看到大约在10Hz和15Hz有两根谱线,幅度对应大约0.75和0.5,这正是我们设定的两个单音正弦信号叠加。(双边频谱非0频处幅度要乘以2)
数据不准确(栅栏效应)以及下方旁瓣效应是因为采样频率和时宽不够大,深层次的原因是计算机中无法真正仿真模拟信号和无限长信号。
符号定义
为了方便理解文章和代码,我使用的是压缩感知理论中惯用符号说明,正如知乎中“稍有常识的人”说写的:
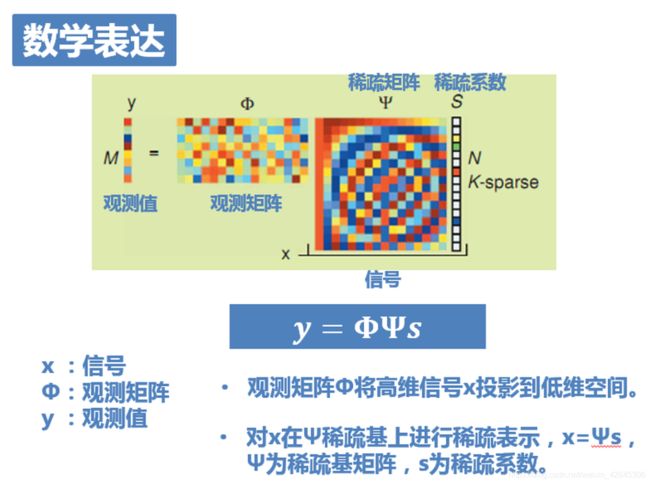
x x x——时域信号,长度为N
y y y——观测信号,长度为M,应有M<
Ψ \Psi Ψ(Psi)——稀疏基矩阵N × \times ×N,这里表示频域转换到时域,有 x = Ψ S x=\Psi S x=ΨS
Φ \Phi Φ(Phi)——观测(测量)矩阵M × \times ×N,表示压缩的过程,后面细讲。
Θ \Theta Θ(Theta)——传感矩阵(亦称感知矩阵)M × \times ×N,有 Θ = Φ Ψ \Theta=\Phi \Psi Θ=ΦΨ,这样等式就可以简化为 y = Θ S y=\Theta S y=ΘS
矩阵向量应该加粗非斜体的,懒得弄了凑合看吧
稀疏基矩阵的构建
在本例中, Ψ \Psi Ψ的构建代码为Psi=inv(fft(eye(N,N)));
表示对单位阵求离散傅里叶变换后再求逆。
先讲一点前置知识,对于长度为N的时域离散信号 x x x来说,其离散傅里叶变换为 S S S,那么它可以写成 S = fft ( x ) S=\text{fft}(x) S=fft(x),也可以写成 S = fft ( I ) x S=\text{fft}(I)x S=fft(I)x,其中 I I I表示N × \times ×N的单位阵。根据离散傅里叶变换的定义可知,它是从0到N-1的乘积求和累加,而求和累加的过程可以视为矩阵中行向量乘以 x x x列向量。而由于单位阵,稀疏基矩阵中只有旋转因子 W N k W_N^k WNk,因此时域信号左乘 fft ( I ) \text{fft}(I) fft(I)就相当于做了傅里叶变换。
因此,将傅里叶变换的矩阵求个逆,就是逆傅里叶变换,即 x = Ψ S x=\Psi S x=ΨS
稀疏矩阵的物理意义,就是把要采样的信号变换到另一个域中,而在这个域中,信号是稀疏的。在本例中,信号在时域并不稀疏,通过傅里叶变换变换到频域后就成为稀疏信号了。同理,也可以使用小波变换、余弦变换等,只要变换后的向量是稀疏的即可。
观测矩阵的构建
观测矩阵这里面有很深的学问,我还没了解清楚。我找到了一篇学长的硕士毕业论文以供参考
【吴赟.压缩感知测量矩阵的研究[D]. 西安电子科技大学硕士学位论文,2012】
大致来讲(可能说的不对,还请批评指正)
Candes、Romberg和Tao指出,要想能解出 y = Θ S y=\Theta S y=ΘS,传感矩阵 Θ \Theta Θ需要满足有限等距性质(Restricted Isometry Property,Rip)
参考自:
E.Candes,J.Romberg,T.Tao.RobuSt uncertainty principles:Exact signal reconstruction from highly incomplete frequency information.IEEE Transactions on Information Theory,2006,v01.52,no.3,PP.489-509.
E.Candes,T.Tao.Decoding by
linear programming.IEEE Transactions on Information Theory,2005,v01.51,no.12,PP.4203-4215.
但是,上述只是一个理论设想,实际上要直接验证矩阵是否满足RIP条件是一件很困难的事情。在实际应用中,我们可以用RIP准则的一种等价情况,即非相干性来指导测量矩阵的设计。所谓非相干性(Incoherence),是指矩阵 Φ \Phi Φ的行向量不能用矩阵 Ψ \Psi Ψ中的列向量稀疏表示。
而Donoho等人指出,服从高斯分布的随机矩阵可以很大概率上满足上述条件,因此随机高斯测量矩阵是常用的测量矩阵,本例中也使用该测量矩阵。

截图源自学长的论文
matlab生成随机高斯测量矩阵的代码:Phi=sqrt(1/M)*randn(M,N);
上述知乎文章中提到,这个测量矩阵的物理意义是对时域信号的随机亚采样(不等间距采样),但是我搜集了很多资料,还是不能理解这个测量矩阵是如何做到随机采样的,而且比较疑惑测量向量 y y y是如何得出来的。现有代码中都是提前知道了 x x x,然后用 y = Θ S y=\Theta S y=ΘS得出,但是实际中得到 x x x的过程本身就已经完成了过采样,那还要压缩感知做什么?
如果测量矩阵 Φ \Phi Φ是一个N × \times ×N的单位阵,那么压缩感知就退化成了普通的采样过程。
稀疏恢复
好,现在问题来了。已知测量向量 y y y和传感矩阵 Θ \Theta Θ,且有 y = Θ S y=\Theta S y=ΘS,如何求解出稀疏向量 S S S?
这就是稀疏恢复问题。
我之前发过的一篇论文研究过这个稀疏恢复问题,当时是使用极大极小值优化算法,感兴趣的可以了解一下:
J. Chen et al., “A Sparsity Based CFAR Algorithm for Dense Radar Targets,” 2020 IEEE Radar Conference (RadarConf20), 2020, pp. 1-6, doi: 10.1109/RadarConf2043947.2020.9266526.
本例中等式不含噪声,我就偷个懒,用matlab的CVX凸优化工具箱。这个工具箱需要安装,先在官网上下载,然后百度一下教程,很容易就安装好了。
由于信号在频域稀疏,即 S S S是一个稀疏信号,因此优化的目标函数可以是 S S S的零范数或者一范数,一范数更好求解一些,因此一范数更常用,具体的数学原理我也不会不讲 。
最终求解的问题如下
m i n ∣ ∣ S ∣ ∣ 1 min ||S||_1 min∣∣S∣∣1
s u b j e c t t o y = Θ S subject\space to \space y=\Theta S subject to y=ΘS
matlab代码如下:
%%使用cvx凸优化工具箱
cvx_startup;
cvx_begin
variable Sp(N) complex;%定义待求解的变量
minimize(norm(Sp,1));%一范数约束表示提高稀疏性
subject to
Theta*Sp==y;%约束条件
cvx_end
优化结果 S p S_p Sp并不是真正稀疏的,其中大部分值都是极其接近于0而不等于0,这些显然应该为0的值,需要我们手动置零来避免其干扰。判定哪些值需要置零而哪些值不需要置零,需要我们设定一个阈值,我这里简单的用 3 σ 3\sigma 3σ法则设定,即threshold=3*std(abs(Sp));别问为什么,问就是一切皆高斯分布
低于阈值以下的值置零,就可以更准确的得到稀疏向量解 S p S_p Sp。
最后用ifft将频域解变换到时域(或者左乘 Ψ \Psi Ψ也行),恢复出最终的时域采样结果。
仿真结果分析
对上述信号进行压缩感知与稀疏恢复处理,恢复出的结果 S p S_p Sp与真值 S S S进行比较,得到下图:
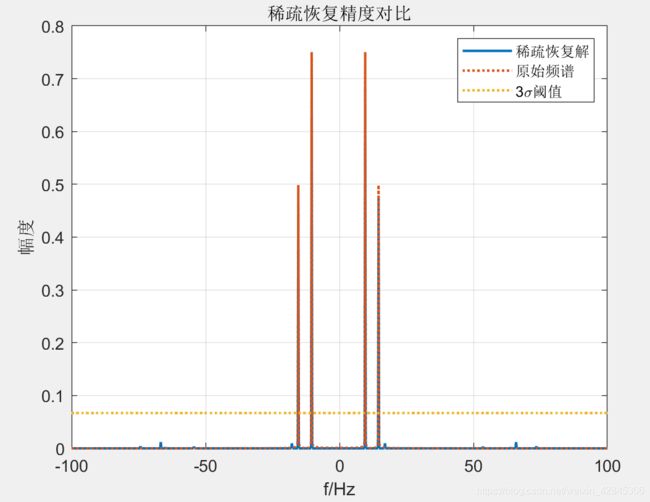
可以看到恢复精度还是很高的。稀疏恢复解有一些毛刺,阈值处理可以很好的消除。
转换到时域观察结果
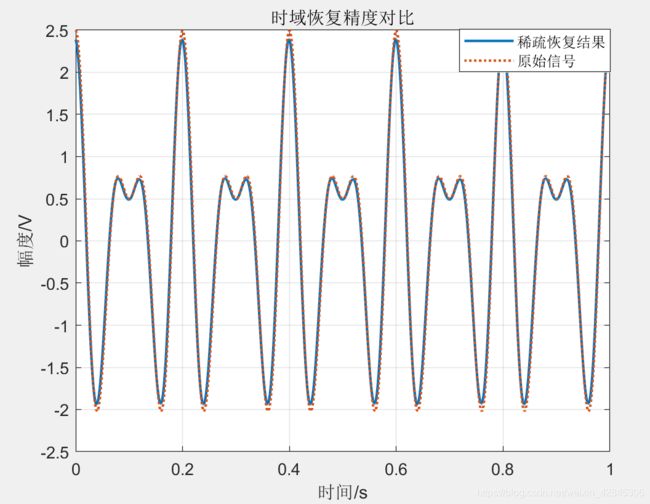
曲线几乎完全重合,使用均方根误差(RMSE)来评估精度,计算出RMSE=0.070639
由于使用的是随机高斯测量矩阵,因此每次试验的值都不一样,但总体RMSE是很低的,表明恢复良好。
之前提到,奈奎斯特采样频率为N_fs=30Hz,时宽为T=5s,因此采样点数为150个点,这是经典理论中要求最少的采样点数。
稀疏恢复理论中指出,观测长度M>=K*log(N/K),K是稀疏度,N信号长度,可以近乎完全重构。在本例中K=2,N=3000,计算出M最小为15。由于要采样的信号不是真正的模拟信号,频域并不是完全稀疏,因此M应该大一些,本例设置为M=30。
对比压缩感知与经典采样理论可以发现,前者只需要长度为30的观测向量,而后者需要长度为150的采样点。压缩感知可以减少80%的采样点,而恢复精度很高,这无疑是一个巨大的进步。
代码
https://download.csdn.net/download/weixin_42845306/20325903
本人尚在初学阶段,难免会有理解错误。如有问题或建议,欢迎评论区留言!