LeetCode_dijkstra 算法_困难_882.细分图中的可到达节点

1.题目

给你一个无向图（原始图），图中有 n 个节点，编号从 0 到 n - 1。你决定将图中的每条边细分为一条节点链，每条边之间的新节点数各不相同。

图用由边组成的二维数组 edges 表示，其中 edges[i] = [u_i, v_i, cnt_i] 表示原始图中节点 u_i 和 v_i 之间存在一条边，cnt_i 是将边细分后的新节点总数。注意，cnt_i == 0 表示边不可细分。

要细分边 [u_i, v_i] ，需要将其替换为 (cnt_i + 1) 条新边，和 cnt_i 个新节点。新节点为 x₁, x₂, …, x_cnti，新边为 [u_i, x₁], [x₁, x₂], [x₂, x₃], …, [x_cnti+1, x_cnti], [x_cnti, v_i] 。

现在得到一个新的细分图 ，请你计算从节点 0 出发，可以到达多少个节点？如果节点间距离是 maxMoves 或更少，则视为可以到达。

给你原始图和 maxMoves ，返回新的细分图中从节点 0 出发可到达的节点数。

示例 1：

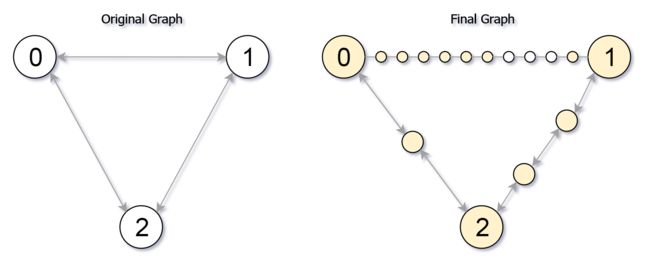
输入：edges = [[0,1,10],[0,2,1],[1,2,2]], maxMoves = 6, n = 3
输出：13
解释：边的细分情况如上图所示。
可以到达的节点已经用黄色标注出来。

示例 2：
输入：edges = [[0,1,4],[1,2,6],[0,2,8],[1,3,1]], maxMoves = 10, n = 4
输出：23

示例 3：
输入：edges = [[1,2,4],[1,4,5],[1,3,1],[2,3,4],[3,4,5]], maxMoves = 17, n = 5
输出：1
解释：节点 0 与图的其余部分没有连通，所以只有节点 0 可以到达。

提示：
0 <= edges.length <= min(n * (n - 1) / 2, 10⁴)
edges[i].length == 3
0 <= u_i < v_i < n
图中不存在平行边
0 <= cnt_i <= 10⁴
0 <= maxMoves <= 10⁹
1 <= n <= 3000

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/reachable-nodes-in-subdivided-graph

2.思路

（1）dijkstra 算法
思路参考本题官方题解。

3.代码实现（Java）

//思路1————dijkstra 算法
class Solution {
    public int reachableNodes(int[][] edges, int maxMoves, int n) {
        List<int[]>[] adList = new List[n];
        for (int i = 0; i < n; i++) {
            adList[i] = new ArrayList<int[]>();
        }
        for (int[] edge : edges) {
            int u = edge[0], v = edge[1], nodes = edge[2];
            adList[u].add(new int[]{v, nodes});
            adList[v].add(new int[]{u, nodes});
        }
        Map<Integer, Integer> used = new HashMap<Integer, Integer>();
        Set<Integer> visited = new HashSet<Integer>();
        int reachableNodes = 0;
        PriorityQueue<int[]> pq = new PriorityQueue<int[]>((a, b) -> a[0] - b[0]);
        pq.offer(new int[]{0, 0});

        while (!pq.isEmpty() && pq.peek()[0] <= maxMoves) {
            int[] pair = pq.poll();
            int step = pair[0], u = pair[1];
            if (!visited.add(u)) {
                continue;
            }
            reachableNodes++;
            for (int[] next : adList[u]) {
                int v = next[0], nodes = next[1];
                if (nodes + step + 1 <= maxMoves && !visited.contains(v)) {
                    pq.offer(new int[]{nodes + step + 1, v});
                }
                used.put(encode(u, v, n), Math.min(nodes, maxMoves - step));
            }
        }

        for (int[] edge : edges) {
            int u = edge[0], v = edge[1], nodes = edge[2];
            reachableNodes += Math.min(nodes, used.getOrDefault(encode(u, v, n), 0) + used.getOrDefault(encode(v, u, n), 0));
        }
        return reachableNodes;
    }

    public int encode(int u, int v, int n) {
        return u * n + v;
    }
}