Retinex图像增强算法
Retinex图像增强算法
- 前言
- 参考
- 一 Retinex理论基础
- 二 单尺度SSR(Single Scale Retinex)原理
- 三 算法的实现流程
- 四 其它Retinex改进算法(了解)
-
- 多尺度的Retinex——MSR
- 彩色恢复多尺度Retinex——MSRCR,MSRCP等
前言
本人第一次写博客,记录整理一下自己学的知识,供大家参考,有写的不好的地方,希望大家谅解。如有错误,希望大家提出,本人予以改正。
本文参考以下文章,如有侵犯,请联系我处理。
参考
参考1
参考2
参考3
一 Retinex理论基础
Retinex理论始于Land和McCann于20世纪60年代作出的一系列贡献,其基本思想是人感知到某点的颜色和亮度并不仅仅取决于该点进入人眼的绝对光线,还和其周围的颜色和亮度有关。Retinex这个词是由视网膜(Retina)和大脑皮层(Cortex)两个词组合构成的。Land之所以设计这个词,是为了表明他不清楚视觉系统的特性究竟取决于此两个生理结构中的哪一个,抑或是与两者都有关系。
Retinex理论基于一下假设:
1.真实世界是无颜色的,我们所感知的颜色是光与物质的相互作用的结果。我们见到的水是无色的,但是水膜—肥皂膜却是显现五彩缤纷,那是薄膜表面光干涉的结果。
2.每一颜色区域由给定波长的红、绿、蓝三原色构成的;
3.三原色决定了每个单位区域的颜色。
Retinex 理论的基本内容:
物体的颜色是由物体对长波(红)、中波(绿)和短波(蓝)光线的反射能力决定的,而不是由反射光强度的绝对值决定的;物体的色彩不受光照非均性的影响,具有一致性,即Retinex理论是以色感一致性(颜色恒常性)为基础的。
不同于传统的线性、非线性的只能增强图像某一类特征的方法,Retinex可以在动态范围压缩、边缘增强和颜色恒常三个方面达到平衡,因此可以对各种不同类型的图像进行自适应的增强。
如下图所示,观察者所看到的物体的图像S是由物体表面对入射光L反射得到的,反射率R由物体本身决定,不受入射光L变化。
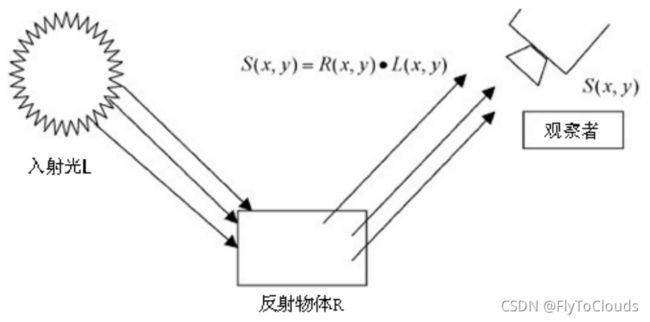
40多年来,研究人员模仿人类视觉系统发展了Retinex算法,从单尺度Retinex算法-SSR,改进成多尺度加权平均的Retinex算法-MSR,再发展成彩色恢复多尺度MSRCR算法和色彩增益加权的AutoMSRCR算法。
本文主要讲解单尺度SSR(Single Scale Retinex)
二 单尺度SSR(Single Scale Retinex)原理
Retinex理论的基本假设是原始图像S是光照图像L和反射率图像R的乘积,即可表示为下式的形式:
S ( x , y ) = R ( x , y ) ∗ L ( x , y ) S(x,y)=R(x,y)*L(x,y) S(x,y)=R(x,y)∗L(x,y)基于Retinex的图像增强的目的就是从原始图像S中估计出光照L,从而分解出R,消除光照不均的影响,以改善图像的视觉效果,正如人类视觉系统那样。在处理中,通常将图像转至对数域,即
s = l o g S ( x , y ) , l = l o g L ( x , y ) , r = l o g R ( x , y ) . . . . . . . . . . . . ( 1 ) s=logS(x,y),l=logL(x,y),r=logR(x,y)............(1) s=logS(x,y),l=logL(x,y),r=logR(x,y)............(1)所以有:
l o g S ( x , y ) = l o g R ( x , y ) + l o g L ( x , y ) . . . . . . . . . . . . . . . . . . . . . . . . . ( 2 ) logS(x,y)=logR(x,y)+logL(x,y).........................(2) logS(x,y)=logR(x,y)+logL(x,y).........................(2)转换得:
r ( x , y ) = l o g R ( x , y ) = l o g S ( x , y ) L ( x , y ) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ( 3 ) r(x,y)=logR(x,y)=log\frac{S(x,y)}{L(x,y)}.............................(3) r(x,y)=logR(x,y)=logL(x,y)S(x,y).............................(3) r ( x , y ) = l o g S ( x , y ) − l o g [ F ( x , y ) ⨂ S ( x , y ) ] . . . . . . . . . . . . ( 4 ) r(x,y)=logS(x,y)−log[F(x,y)⨂S(x,y)]............(4) r(x,y)=logS(x,y)−log[F(x,y)⨂S(x,y)]............(4)
这里, r ( x , y ) r(x, y) r(x,y)是输出图像,上式中后面中括号里的运算是卷积运算。 F ( x , y ) F(x, y) F(x,y)是中心环绕函数,表示为:
F ( x , y ) = λ e − ( x 2 + y 2 ) c 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ( 5 ) F(x,y)=\lambda e^{\frac{-(x^2+y^2)}{c^2}}..................................................(5) F(x,y)=λec2−(x2+y2)..................................................(5)式中 c c c是高斯环绕尺度, λ λ λ是一个尺度,它的取值必须满足下式:
∫ ∫ F ( x , y ) d x d y = 1.............................................. ( 6 ) \int \int F(x,y)dxdy=1..............................................(6) ∫∫F(x,y)dxdy=1..............................................(6)上面的式中可以看出,SSR算法中的卷积是对入射图像的计算,其物理意义是通过计算像素点与周围区域在加权平均的作用下,估计图像中照度的变化,并将 L ( x , y ) L(x,y) L(x,y)去除,只保留 S ( x , y ) S(x,y) S(x,y)属性。
三 算法的实现流程
1)将图像进行log变换
2)然后将log图像进行高斯模糊
3)利用原图和模糊之后的log图像做差分
单尺度Retinex算法SSR的实现流程可以概括如下:
- 读原图 S ( x , y ) S(x, y) S(x,y):
若原图为灰度图:将图像各像素的灰度值由整数型(int)转换为浮点数(float),并转换到对数域;
若原图为彩色图:将颜色分通道处理,每个分量像素值由整数型(int)转换为浮点数(float),并转换到对数域; - 输入高斯环绕尺度 c c c,把积分运算离散化,转为求和运算,通过上式(5)(6)确定λ的值;
- 由式(4)得 r ( x , y ) r(x, y) r(x,y);
若原图是灰度图,则只有一个 r ( x , y ) r(x, y) r(x,y);
若原图为彩色图,则每个通道都有一个对应的 r ( x , y ) r(x, y) r(x,y); - 将 r ( x , y ) r(x, y) r(x,y)从对数域转换到实数域,得到输出图像 R ( x , y ) R(x, y) R(x,y);
- 此时的 R ( x , y ) R(x, y) R(x,y)值的范围并不是0–255,所以还需要进行线性拉伸并转换成相应的格式输出显示。
前面的公式中,中心环绕函数 F ( x , y ) F(x, y) F(x,y)用的是低通函数,这样能够在算法中估计出入射图像对应原始图像的低频部分。从原始图像中除去低频照射部分,就会留下原始图像所对应的高频分量。高频分量很有价值,因为在人类的视觉系统中,人眼对边缘部分的高频信息相当敏感,所以SSR算法可以较好的增强图像中的边缘信息。
由于SSR算法中所选用的高斯函数特点,对于动态范围大幅度压缩和对比度增强两个指标,增强后的图像不能同时保证。但是为了平衡两种增强效果,就必须选择一个较为恰当的高斯尺度常量C。C值一般取值在80–100之间。
四 其它Retinex改进算法(了解)
多尺度的Retinex——MSR
通俗解释:就是再多个单尺度Retinex做平均,区别是在第二步高斯模糊是选择的sigma是不同的
原始图像进行三次SSR
高斯模糊选择15,80,200作为高斯模糊sigma参数
对三次的SSR结果做平均即为MSR图像
彩色恢复多尺度Retinex——MSRCR,MSRCP等
对多尺度MSR结果做了色彩平衡,归一化,增益和偏差线性加权