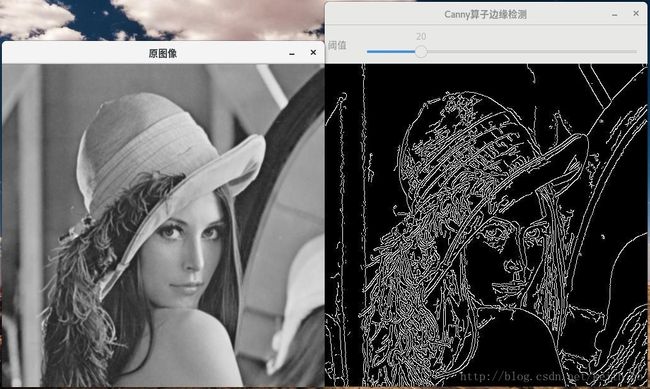
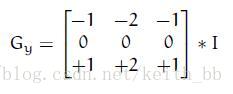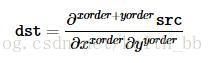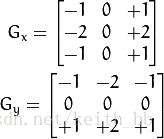opencv学习(三十二)之图像边缘检测Soble_Laplace_Canny

1. Sobel算子

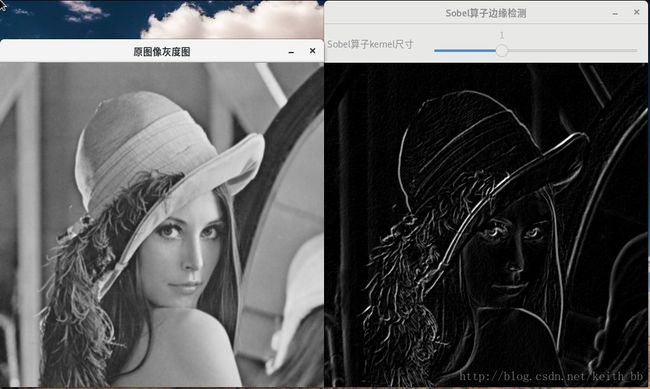
前面我们已经介绍了图像的卷积操作，而一个最重要的卷积运算就是对导数的计算，假设我们需要检测图像中的边缘部分，如下图所示：

前面我们介绍图像的高频和低频分量的时候说到，图像的高频分量一般出现在像素值显著改变的地方，而高频分量的出现就容易勾画出图像的轮廓。在高等数学中我们知道函数变化剧烈其所对应的导数值越大(极大值)，所以表示图像像素值改变最大的一个方法就是求出图像的导数。其梯度值剧烈的改变预示着图像中内容发生显著变化。假设我们有一张一维图像，图中灰度值的“跃升”表示边缘的存在：

通过对函数进行一阶微分我们可以更加清晰的看到边缘“跃升”的存在，即在其一阶微分中最大值代表其所对应的像素值变化剧烈。如下图：

从上面的介绍中我们可以推测对于图像边缘的检测可以通过定位梯度值大于邻域的像素的方法找到（或者推广到大于一个阈值即可认为是图像边缘）

Sobel算子是一个离散微分算子(discrete differentiation operator),它用来计算图像灰度函数的近似梯度并结合了高斯平滑和微分求导。假设被处理的图像位I, Sobel算子数学表达公式如下：

1.1在两个方向求导

• .a 水平变化：将I与一个奇数大小的内核Gx进行卷积，比如当内核大小为3时，Gx计算结果为：
  
• .b 垂直变化：将I与一个奇数大小的内核Gy进行卷积，比如当内核大小为3时，Gy的计算结果为：
  

1.2 在图像的每一点结合以上两个结果求出近似梯度：

有时也使用如下更简单的公司代替：

注意
当内核大小为3时，Sobel内核可能产生比较明显的误差，毕竟Sobel算子只是求取了导数的近似值，为了解决这一问题，opencv提供了Scharr函数，但该函数仅作用于大小为3的内核，该函数的运算与Sobel函数一样快，但结果更加精确，其内核如下：

关于Scharr的更多信息请点击

opencv中提供了sobel函数，其定义如下：

void cv::Sobel  ( InputArray  src,  
  OutputArray  dst,  
  int  ddepth,  
  int  dx,  
  int  dy,  
  int  ksize = 3,  
  double  scale = 1,  
  double  delta = 0,  
  int  borderType = BORDER_DEFAULT  
 ) 

当ksize=1时，内核形式为3x1或1x3(没有高斯平滑)，ksize=1只能用于一阶或二阶x或y方向上的导数。当ksize=CV_SCHARR(-1)是一个特殊值，将会调用同样为3x3内核比Sobel计算的结果精确的Scharr滤波器。Scharr的核心是：

函数通过一个恰当的内核与图像进行卷积来计算图像导数，如下：

sobel算子结合高斯平滑和分化，所以结果有更好的抗噪性。通常这个函数设置为(xorder = 1, yorder = 0, ksize = 3)来计算图像在x方向上的导数，此时的核如下：

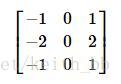
或(xorder = 0, yorder = 1, ksize = 3)来计算y方向图像导数，此时的核如下：

参数解释

• . InputArray src: 输入图像
• . OutputArray dst: 输出图像
• . int ddepth: 输出图像深度，与输入图像深度对应关系如下表所示：
  
  当输入图像为8-bit时将会导致截断。
• . int dx: x方向上的差分阶数
• . int dy: y方向上的差分阶数
• . int ksize = 3: Sobel函数核尺寸，只能是1、3、5、7中的一个，默认值是3
• . double scale = 1: 计算导数值可选的缩放银子，默认值是1表示没有缩放。可以通过查看函数getDerivKernels()获取更加详细的信息
• . int borderType = BORDER_DEFAULT:边界模式，可以查询borderInterpolate得到详细信息。

示例代码

#include 
#include 
#include 
#include 

using namespace std;
using namespace cv;

//声明全局变量
const int sobel_kernel_size_maxValue = 3;   //kernel尺寸最大值
int sobel_kernel_size_value;                //kernel尺寸

Mat srcImage, dstImage, grayImage, x_gradImage, y_gradImage;
Mat x_abs_gradImage, y_abs_gradImage;
String windowName = "Sobel算子边缘检测";

int depth = 0;      //输出图像与原图像一致
int scale = 1;      //可选缩放因子
int delta = 0;      //可选的delta

//声明轨迹条回调函数
void sobelFun(int, void*);

int main()
{
    srcImage = imread("lena.jpg");

    //判断图像是否加载成功
    if(srcImage.empty())
    {
        cout << "图像加载失败!" << endl;
        return -1;
    }
    else
        cout << "图像加载成功!" << endl << endl;

    //高斯滤波
    GaussianBlur(srcImage, srcImage, Size(3, 3), 0, 0, BORDER_DEFAULT);

    cvtColor(srcImage, grayImage, COLOR_BGR2GRAY);   //图像转换灰度图
    namedWindow("原图像灰度图", WINDOW_AUTOSIZE);
    imshow("原图像灰度图", grayImage);

    namedWindow(windowName, WINDOW_AUTOSIZE);       //创建窗口

    //设置轨迹条属性
    sobel_kernel_size_value = 1;
    char kernelSizeName [20];
    sprintf(kernelSizeName, "Sobel算子kernel尺寸", sobel_kernel_size_maxValue);

    //创建轨迹条
    createTrackbar(kernelSizeName, windowName, &sobel_kernel_size_value,
                    sobel_kernel_size_maxValue, sobelFun);

    //调用回调函数
    sobelFun(sobel_kernel_size_value, 0);

    waitKey(0);

    return 0;
}

//回调函数
void sobelFun(int, void*)
{
    //重新计算尺寸kernel尺寸数值
    int kernelvalue;
    kernelvalue = sobel_kernel_size_value * 2 + 1;

    //计算x方向梯度
    Sobel(grayImage, x_gradImage, depth, 1, 0, kernelvalue, scale, delta, BORDER_DEFAULT);
    convertScaleAbs(x_gradImage, x_abs_gradImage);
    namedWindow("x方向的sobel边缘检测", WINDOW_AUTOSIZE);
    imshow("x方向的sobel边缘检测", x_abs_gradImage);

    //计算y方向梯度
    Sobel(grayImage, y_gradImage, depth, 0, 1, kernelvalue, scale, delta, BORDER_DEFAULT);
    convertScaleAbs(y_gradImage, y_abs_gradImage);
    namedWindow("y方向上的sobel边缘检测", WINDOW_AUTOSIZE);
    imshow("y方向上的sobel边缘检测", y_abs_gradImage);

    //将x方向和y方向的梯度叠加
    addWeighted(x_abs_gradImage, 0.5, y_abs_gradImage, 0.5, 0, dstImage);


    imshow(windowName, dstImage);
}

代码解释：

• .Sobel算子一般与高斯滤波配合使用
• .convertScaleAbs()函数的作用是对求得的结果取绝对值并将结果转换成8-bit.

运行结果如下：

2.Laplace算子

Sobel算子是基于在边缘部分，像素值会出现较大的变化，因此在边缘部分求取一阶导数可以得到极值点，如果在边缘部分求二阶导呢？如下图：


在一阶导数的极值位置，二阶导数为0.所以也可以利用这个特点来作为检测图像边缘的方法，但是二阶导数的0值不仅仅出现在边缘，它们也可能出现在无意义的位置，但我们可以过滤掉这些点。因为图像是二维的，需要在两个方向求导，opencv提供了Laplacian函数来实现，使用Laplacian算子将会使求导过程变得简单。Laplacian算子定义如下：

Laplacian函数定义如下：

void cv::Laplacian  (   InputArray      src,
        OutputArray     dst,
        int     ddepth,
        int     ksize = 1,
        double      scale = 1,
        double      delta = 0,
        int     borderType = BORDER_DEFAULT 
    )

参数解释

• .src: 输入图像
• . dst: 输出图像
• . ddepth:图像深度
• . ksize: 用于计算二阶导的kernel尺寸，可以查看getDerivKernels函数查看详细信息，尺寸必须是正奇数。
• . scale: Laplacian算子的可选因子，有默认值1，此时没有应用缩放因子，可查看getDerivKernels查看详细信息
• . delta: 存储目标图像前可选的delta值，有默认值0
• . borderType:用于推断边界像素的模式，有默认值BORDER_DEFAULT

函数只有在ksize>1时才能正常计算，当ksize==1时，Laplacian将由下面的模板进行计算：

实际上，由于Laplacian使用了图像梯度，它内部调用了Sobel算子。

示例代码

#include 
#include 
#include 
#include 

using namespace std;
using namespace cv;

//声明全局变量
Mat srcImage, grayImage, dstImage, dst_absImage;
const int scale = 1;
const int delta = 0;
const int ddepth = CV_16S;
const int kernelSizeMaxValue = 3;
int kernelSizeValue;

//声明回调函数
void laplacianFun(int, void*);
String windowName = "Laplace算子边缘检测";

int main()
{
    srcImage = imread("lena.jpg");

    //判断图像是否加载成功
    if(srcImage.empty())
    {
        cout << "图像加载失败!" << endl;
        return -1;
    }
    else 
        cout << "图像加载成功!" << endl << endl;

    //对图像进行高斯滤波操作
    GaussianBlur(srcImage, srcImage, Size(3, 3), 0, 0, BORDER_DEFAULT);
    cvtColor(srcImage, grayImage, COLOR_BGR2GRAY);      //将图像转换为灰度图
    namedWindow("原图像", WINDOW_AUTOSIZE);
    imshow("原图像", grayImage);

    namedWindow(windowName, WINDOW_AUTOSIZE);
    kernelSizeValue = 1;        //轨迹条初始值为1
    char trackbarName[20];      //轨迹条名称
    sprintf(trackbarName, "laplacian算子kernel尺寸", kernelSizeMaxValue);

    //创建轨迹条
    createTrackbar(trackbarName, windowName, &kernelSizeValue, kernelSizeMaxValue, laplacianFun);
    laplacianFun(kernelSizeValue, 0);       //调用回调函数

    waitKey(0);

    return 0;
}

void laplacianFun(int, void*)
{
    //重新计算kernel的尺寸
    int kernelSize;
    kernelSize = kernelSizeValue * 2 + 1;

    Laplacian(grayImage, dstImage, ddepth, kernelSize, scale, delta, BORDER_DEFAULT);
    convertScaleAbs(dstImage, dst_absImage);
    imshow(windowName, dst_absImage);
}

运行结果

3.Canny算子

Canny边缘检测算法时John F. Canny于1986年开发出来的一个多级边缘检测算法，也被很多人认为时边缘检测的最优算法，，最有边缘检测的三个主要评价标准是：

• .低错误率: 标识出尽可能多的实际边缘，同时尽可能的减少噪声产生的误报
• .高定位性：标识处的边缘要与图像中的世纪边缘尽可能接近
• .最小响应：图像中的边缘只能标识一次。

Canny边缘检测的步骤如下：

3.1消除噪声

使用高斯平滑滤波器卷积降噪，下面显示了一个size = 5的高斯内核

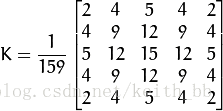
3.2计算梯度幅值和方向

此处按照Sobel滤波器的步骤

• a.运用一对卷积阵列分别作用于x和y方向
  
• b.使用下列公式计算梯度幅值和方向
  

梯度方向近似得到四个可能角度之一(一般0，45，90，135)

3.3非极大值抑制

这一步排除非边缘像素，仅仅保留了一些细线条(候选边缘)

3.4滞后阈值

最后一步，Canny使用了滞后阈值，滞后阈值需要两个阈值(高阈值和低阈值)

• a.如果某一像素位置的幅值超过高阈值，该像素被保留为边缘像素。
• b.如果某一像素的幅值小于低阈值，该像素被排除
• c.如果某一像素位置的幅值在两个阈值之间，该像素仅仅在连接到一个高于高阈值的像素时被保留。

Canny推荐的高低阈值比在2：1到3：1之间

opencv提供了两种形式的Canny函数定义，分别如下：

void cv::Canny  (   InputArray      image,
        OutputArray     edges,
        double      threshold1,
        double      threshold2,
        int     apertureSize = 3,
        bool    L2gradient = false 
    )   

参数解释：

• .Image: 8-bit输入图像
• .edges: 输出的边缘图像，8-bit单通道图像，与输入图像有相同的尺寸。
• .threshold1: 第一个滞后性阈值
• .threshold2: 第二个滞后性阈值
• .apertureSize: 表示应用的Sobel算子孔径大小，有默认值3
• .L2gradient: 一个计算图像梯度幅值的标识，有默认值false

第二种定义形式如下：

void cv::Canny  (   InputArray      dx,
        InputArray      dy,
        OutputArray     edges,
        double      threshold1,
        double      threshold2,
        bool    L2gradient = false 
    )   

我们可以看到这种定义形式只是在输入图像与第一种输入图像不同，针对其输入解释如下：

• .dx: 16-bit 输入图像x方向(CV_16SC1或CV_16SC3)
• .dy: 16-bit输入图像y方向，与dx类型一样
• . 其它参数解释请参考第一种定义形式

注意
对于threshold1和threshold2两个阈值来讲，两者较小的值用于边缘连接而较大的值用来寻找边缘的初始段。

示例代码

#include 
#include 
#include 
#include 

using namespace std;
using namespace cv;

//声明全局变量
Mat srcImage, grayImage, dstImage;
int edgeThresh = 1;
int lowThreshold;
int const max_lowThreshold = 100;
int ratio = 3;           //阈值倍数
int kernel_size = 3;    //Sobel算子孔径尺寸
String windowName =  "Canny算子边缘检测";

//声明回调函数
void CannyThreshold(int, void*);

int main()
{
    srcImage = imread("lena.jpg");

    //判断图像是否加载成功
    if(srcImage.empty())
    {
        cout << "图像加载失败!" << endl;
        return -1;
    }
    else
        cout << "图像加载成功!" << endl << endl;

    //高斯滤波
    GaussianBlur(srcImage, srcImage, Size(3, 3), 0, 0, BORDER_DEFAULT);
    cvtColor(srcImage, grayImage, COLOR_BGR2GRAY);

    namedWindow("原图像", WINDOW_AUTOSIZE);
    imshow("原图像", grayImage);

    //定义轨迹条属性
    namedWindow(windowName, WINDOW_AUTOSIZE);
    char trackbarName[20];
    sprintf(trackbarName, "阈值", max_lowThreshold);
    lowThreshold = 20;

    //创建轨迹条
    createTrackbar(trackbarName, windowName, &lowThreshold, max_lowThreshold, CannyThreshold);
    CannyThreshold(lowThreshold, 0);

    waitKey(0);

    return 0;
}

void CannyThreshold(int, void*)
{
    Canny(grayImage, dstImage, lowThreshold, lowThreshold*ratio, kernel_size);

    imshow(windowName, dstImage);
}

运行结果如下：