pytorch底层
1、L2normalize:L2归一化:将一组数变成0-1之间。pytorch调用的函数是F.normalize。一般池化后会有一层l2norm层。

# l2norm 的实现如下
x = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
norm = x.pow(p).sum(1, keepdim=True).pow(1./ p) # l2norm p=2
print(norm)
out = x.div(norm)
print(out)
2、torch的几种矩阵乘法
点乘法
(1)torch.mul 点乘法
用法与*乘法相同,也是element-wise的乘法,也是支持broadcast的。
>>> a = torch.ones(3,4)
>>> a
tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
>>> b = torch.Tensor([1,2,3,4])
>>> b
tensor([1., 2., 3., 4.])
>>> torch.mul(a, b)
tensor([[1., 2., 3., 4.],
[1., 2., 3., 4.],
[1., 2., 3., 4.]])
(2)* 点乘
点积是两个维度相同的矩阵(不相同就broadcast成相同),相应位置的值做乘法,最后返回的矩阵和原矩阵是同型的。点积是broadcast的。
>>> a = torch.tensor([[1, 2], [2, 3]])
>>> a * a
tensor([[1, 4],
[4, 9]])
矩阵乘法
(3)torch.mm:矩阵乘法
数学里的矩阵乘法,要求两个Tensor的维度满足矩阵乘法的要求,即不可用广播机制
>>> a = torch.ones(3,4)
>>> b = torch.ones(4,2)
>>> torch.mm(a, b)
tensor([[4., 4.],
[4., 4.],
[4., 4.]])
(4)torch.matual 矩阵乘法
torch.mm的broadcast版本,即可以用广播机制
>>> a = torch.ones(3,4)
>>> b = torch.ones(5,4,2)
>>> torch.matmul(a, b)
tensor([[[4., 4.],
[4., 4.],
[4., 4.]],
[[4., 4.],
[4., 4.],
[4., 4.]],
[[4., 4.],
[4., 4.],
[4., 4.]],
[[4., 4.],
[4., 4.],
[4., 4.]],
[[4., 4.],
[4., 4.],
[4., 4.]]])
(5)@ 矩阵乘法
a = torch.tensor([[1, 2, 3], [4, 5, 6]]) # 2*3
b = torch.tensor([[1, 2], [3, 4], [5, 6]]) # 3*2
c = a @ b
c
>>>
tensor([[22, 28],
[49, 64]])
(6)torch.bmm(a, b):计算两个tensor的矩阵乘法,tensor a 的size为(b,h,w),tensor b的size为(b,w,h),注意两个tensor的维度必须为3.
numpy也有几种乘法,参考 numpy的乘法API
3、with torch.no_grad(): with是python中上下文管理器,简单理解,当要进行固定的进入,返回操作时,可以将对应需要的操作,放在with所需要的语句中。比如文件的写入(需要打开关闭文件)等。
使用了with torch.no_grad()::在该模块下返回的tensor没有grad_fn=属性,即所有计算得出的tensor的requires_grad都自动设置为False。不使用with torch.no_grad()::返回的tensor有grad_fn=属性,表示计算的结果在计算图当中,可以进行梯度反传等操作。即使一个 tensor(命名为x)的requires_grad = True,在with torch.no_grad()计算,由x得到的新 tensor(命名为w-标量)requires_grad也为False,且grad_fn也为None,即不会对w求导。
参考:with torch.no_grad():用法详解
=======================================
4、torch中的register_buffer()的使用(MoCo里面使用了)
参考:Pytorch中的register_buffer()。推荐程度: ⋆ ⋆ ⋆ ⋆ ⋆ \star\star\star\star\star ⋆⋆⋆⋆⋆
4.1、使用方法:self.register_buffer('my_buffer2', self.tensor2)放在类的成员里。一般的tensor类型的类成员(如self.tensor=xxx)是不会算到model.state_dict()中的,而且也不会随着模型的移动而移动。
4.2、在pytorch模型的保存中,一般用torch.save(model.state_dict()),model.state_dict()是一个字典,里边存着我们模型各个部分的参数。在model中,我们需要更新其中的参数,将训练结束将参数保存下来。但在某些时候,我们可能希望模型中的某些参数不更新(从开始到结束均保持不变),但又希望参数保存下来(model.state_dict() ),这时我们就会用到register_buffer()。
通过register_buffer()登记过的张量:会自动成为模型中的参数,随着模型移动(gpu/cpu)而移动,但是不会随着梯度进行更新。
4.3、parameter和buffer的区别
模型保存下来的参数有两种:一种是需要更新的Parameter,另一种是不需要更新的buffer。在模型中,利用backward反向传播,可以通过requires_grad来得到buffer和parameter的梯度信息,但是利用optimizer进行更新的是parameter,buffer不会更新,这也是两者最重要的区别。这两种参数都存在于model.state_dict()的OrderedDict中,也会随着模型“移动”(model.cuda())。
4.4、 对模型中的buffer进行访问
与model.parameters()和model.named_parameters()相同,model.buffers()和model.named_buffers可以对模型中的buffer进行访问,只是一个是对模型中的parameter访问,一个是对模型中的buffer访问。
4.5、Buffer变量可以通过backward()得到梯度信息
buffer变量和parameter变量一样,都可以通过backward()得到梯度信息,但区别是优化器optimizer更新的parameter变量,所以buffer并不会更新。即buffer可以求梯度,但是不会梯度更新。
4.6、Buffer变量不需要求梯度时,可通过Parameter代替
在构造模型时候,可以将某些Parameter从模型中通过.detach()方法或直接将Parameter的requires_grad设置为False,使得此变量不求梯度,也可达到不更新的效果。
- 通过
nn.Paramter()将张量设置为变量,同时设置requires_grad为False - 这个变量也会随着模型保存,并且随着模型“移动”
- 可达到与
buffer相同的效果
4.7、既然Parameter的requires_grad设置为False也可以达到与buffer相同的效果,那么为什么要存在buffer?
buffer与parameter具有 “同等地位”,所以将某些不需要更新的变量“拿出来”作为buffer,可能更方便操作,可读性也更高,对Paramter的各种操作(固定网络的等)可能也不会“误伤到” buffer这种变量。buffer最重要的意义应该是需要得到梯度信息时,不会更新因为optimizer而更新,这也是parameter所不能代替的。
=======================================
3、torch的几种损失函数
(1)torch.nn.CrossEntropyLoss()
1.1、函数原型如下图所示:

可以看出,torch.nn.CrossEntropyLoss()这个类其实是调用了F.cross_entropy()。F.cross_entropy()的函数原型如下
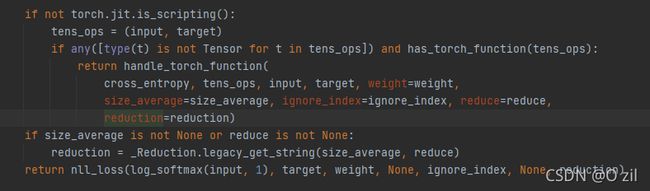
可见,F.cross_entropy()其实是调用了nll_loss,而且看到log_softmax(input, dim=1)可知已经为input做了log_softmax操作。
综上,CrossEntropyLoss就是把以上Softmax–Log–NLLLoss合并成一步
CELoss和NLLLoss
交叉熵损失函数
1.2、交叉熵损失(凸函数–有全局最优值)的数学公式
(1)二分类
在二分的情况下,模型最后需要预测的结果只有两种情况,对于每个类别我们的预测得到的概率为 p p p 和 1 − p 1-p 1−p ,此时表达式为:
L = 1 N ∑ i L i = 1 N ∑ i − [ y i ∗ l o g ( p i ) + ( 1 − y i ) ∗ l o g ( 1 − p i ) ] L = \frac{1}{N}\sum_{i}{L_i}=\frac{1}{N}\sum_{i}{-[y_i \ast log(p_i)+(1-y_i) \ast log(1-p_i)]} L=N1i∑Li=N1i∑−[yi∗log(pi)+(1−yi)∗log(1−pi)]
其中:
y i y_i yi----表示样本 i i i的label,正类为1, 负类为0
p i p_i pi—表示样本 i i i预测为正类的概率
(2)多分类
多分类是对二分类的扩展:
L = 1 N ∑ i L i = − 1 N ∑ i ∑ c = 1 M y i c ∗ l o g ( p i c ) L = \frac{1}{N}\sum_{i}{L_i}=-\frac{1}{N}\sum_{i}{\sum_{c=1}^{M}{y_{ic} \ast log(p_{ic})}} L=N1i∑Li=−N1i∑c=1∑Myic∗log(pic)
其中:
N N N-------样本的数量
M M M------类别的数量
y i c y_{ic} yic----符号函数(0 or 1)(也就是ont-hot),表示样本 i i i的真实类别,如果样本 i i i的真实类别等于 c c c取1, 否则取0
p i c p_{ic} pic----观测样本 i i i属于类别 c c c的预测概率
1.3 交叉熵的神经网络过程
step1:神经网络最后一层的预测值(最后一层的维度一般为类别数),也就是每个类别的得分(logits)
step2:由于对各个类别的预测值之和为1,所以要对预测值做归一化,一般是用softmax或者sigmoid(二分类)得到交叉熵公式中的预测概率 p i p_i pi. Sigmoid函数与Softmax函数的区别与联系
step3:然后计算 l o g ( p i ) log(p_i) log(pi)
step4:最后通过 o n e − h o t one-hot one−hot计算最后的loss
第4步被 NLLoss一部搞定,NLLLoss的结果就是把Softmax–Log后输出与Label对应的那个值拿出来,再去掉负号,再求均值。
(3) 多标签分类
参考:各种损失函数
4、pytorch的各种包
torch.utils.data模块提供了有关数据处理的工具,torch.nn模块定义了大量神经网络的层,torch.nn.init模块定义了各种初始化方法,torch.optim模块提供了很多常用的优化算法。
5、pytorch的permute、view、reshape、transpose
pytorch中reshape()、view()、permute()、transpose()总结
(1)view 和 reshape
ytorch中reshape、view以及resize_之间的区别
.view()方法只能改变连续的(contiguous)张量,否则需要先调用.contiguous()方法来返回一个 contiguous copy;而.reshape()方法不受此限制;如果对tensor调用过transpose,permute等操作的话会使该tensor在内存中变得不再连续。view()操作后的tensor和原tensor共享存储。如果不想共享内存,应该用clone()拷贝一个新的tensor。.view()方法返回的张量与原张量共享基础数据(存储器,注意不是共享内存地址), 如果原tensor改变,转变后的tensor也会变化,如果转变后的tensor变换,原tensor也会变化。如果不想共享,应该用clone()拷贝一个新的tensor;.reshape()方法返回的可能是原张量的copy,也可能不是,这个我们不知道,所以尽量避免使用reshape(),判断是否contiguous用torch.Tensor.is_contiguous()函数。reshape/view在改变形状的时候,总的数据个数不能变。resize_在改变形状的时候是可以只截取一部分数据的。
(2)permute()和transpose()
两者都是实现维度之间的交换,transpose 只能一次转换两个维度,permute 可以一次转换多个维度,permute 可以通过 transpose 组合的形式实现。
(3)view 和 permute 的区别
a = torch.arange(5).repeat((6, 1)) # 6*5
print(a)
a = a.view(5, 6) # 5*5
print(a.is_contiguous()) # true
a
>>>
before_a:
tensor([[0, 1, 2, 3, 4],
[0, 1, 2, 3, 4],
[0, 1, 2, 3, 4],
[0, 1, 2, 3, 4],
[0, 1, 2, 3, 4],
[0, 1, 2, 3, 4]])
after_a: # view相当于将 a 矩阵里的数全都展平了,然后按照要求每一维按顺序挑数
tensor([[0, 1, 2, 3, 4, 0],
[1, 2, 3, 4, 0, 1],
[2, 3, 4, 0, 1, 2],
[3, 4, 0, 1, 2, 3],
[4, 0, 1, 2, 3, 4]])
b = torch.arange(5).repeat((6, 1))
b = b.permute(1, 0)
# b = b.transpose(1, 0)
print(b.is_contiguous()) # false,用permute和transpose转置都是 false
b
>>> # permute 是更灵活的transpose(因为transpose只支持两个维度的变),只是做维度的变换,不改变维度里的数据分布
tensor([[0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1],
[2, 2, 2, 2, 2, 2],
[3, 3, 3, 3, 3, 3],
[4, 4, 4, 4, 4, 4]])
6、numpy的copy()和torch的clone()、detach()
numpy和torch的拷贝
(1) numpy的copy()得到占据不同内存空间的array
(2) torch的clone和numpy的copy功能类似,开辟新的内存空间,但多了梯度的处理细节
(3) torch的detach只是起到取出数据(不带梯度)做处理的作用,处理的数据还是反映在原内存空间,所以一般不想让数据有梯度的回传就可以用tensor.detach().clone()
7、python的set()方法,返回一个无序不重复的元素集合。python里有set数据类型。
a = [1, 2, 3, 2, 6, 7, 8, 7]
b = set(a)
type(set(a)) # set类型,也就是集合类型
b
>>>
{1, 2, 3, 6, 7, 8} # 去重了,而且排序了
list(set(a))
>>>
[1, 2, 3, 6, 7, 8] # 转变为列表类型
8、torch.gather()的用法
torch.gather()可以实现从某个矩阵中按照某个维度找出某些满足条件的值。一般用法如下X.gather(1, index_tensor)或torch.gather(X, 1, index_tensor),注意第三个参数index_tensor表示的是索引,也就是满足条件的值
比如:
import torch
a = torch.tensor([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10], [11, 12, 13, 14, 15] ])
index = torch.tensor([[0, 2],[3, 4], [1, 4]])
print(torch.gather(a, 1, index)) # 挑出第一维度的index值
>>>
tensor([[ 1, 3],[ 9, 10],[12, 15]])
用torch.gather()实现CE_loss
C r o s s E n t r o p y L o s s = − 1 N ∑ i = 1 N ∑ j = 1 M y i j l o g y ^ i j CrossEntropy Loss = -\frac{1}{N} \sum_{i=1}^{N} \sum_{j=1}^{M} y_{ij}log\hat{y} _{ij} CrossEntropyLoss=−N1i=1∑Nj=1∑Myijlogy^ij
其中 N N N为样本数, M M M为类别数。 y i j y_{ij} yij一般用 one-hot 编码,所以可以用 gather() 实现
def ce_loss(y_hat, y):
return - torch.log(y_hat.gather(1, y.view(-1, 1))) # 这里没有除batch-size
深度学习各种常见功能的代码
softmax函数实现
s o f t m a x = e x i ∑ i = 1 N e x i softmax = \frac{e^{x_i}}{\sum_{i=1}^{N}e^{x_i}} softmax=∑i=1Nexiexi
def softmax(X):
X_exp = X.exp()
partition = X_exp.sum(dim=1, keepdim=True) # 这个 keepdim 只是保持 dim=1(列)的维度
return X_exp / partition
用torch.gather()实现CE_loss
C r o s s E n t r o p y L o s s = − 1 N ∑ i = 1 N ∑ j = 1 M y i j l o g y ^ i j CrossEntropy Loss = -\frac{1}{N} \sum_{i=1}^{N} \sum_{j=1}^{M} y_{ij}log\hat{y} _{ij} CrossEntropyLoss=−N1i=1∑Nj=1∑Myijlogy^ij
其中 N N N为样本数, M M M为类别数。 y i j y_{ij} yij一般用 one-hot 编码,所以可以用 gather() 实现
def ce_loss(y_hat, y):
return - torch.log(y_hat.gather(1, y.view(-1, 1))) # 这里没有除batch-size**
ce loss和softmax可以直接用loss = nn.CrossEntropyLoss()直接搞定
准确率的计算
def evaluate_accuracy(data_iter, y_hat):
acc_sum, n = 0.0, 0
for X, y in data_iter:
acc_sum += (y_hat.argmax(dim=1) == y).float().sum().item() # 求出预测正确的样本数
n += y.shape[0] # 该 batch 的样本数
# acc_sum += (y_hat.argmax(dim=1) == y).float().mean().item() # 或者这样写直接一步到位
return acc_sum / n # 正确的样本数 / 该 batch 中的总样本数
relu激活函数的实现
R e L U ( x ) = m a x ( x , 0 ) ReLU(x)=max(x,0) ReLU(x)=max(x,0)
def relu(X):
return torch.max(input=X, other=torch.tensor(0.0))
手动实现多层感知机
num_inputs, num_outputs, num_hiddens = 784, 10, 256
W1 = torch.tensor(np.random.normal(0, 0.01, (num_inputs, num_hiddens)), dtype=torch.float)
b1 = torch.zeros(num_hiddens, dtype=torch.float)
W2 = torch.tensor(np.random.normal(0, 0.01, (num_hiddens, num_outputs)), dtype=torch.float)
b2 = torch.zeros(num_outputs, dtype=torch.float)
params = [W1, b1, W2, b2]
for param in params:
param.requires_grad_(requires_grad=True)
def MLP(X): # 定义一个两层的多层感知机
X = X.view((-1, num_inputs))
H = relu(torch.matmul(X, W1) + b1)
return torch.matmul(H, W2) + b2
实现权重衰减(L2正则化)权重衰减
l ( w 1 , w 2 , b ) + λ 2 n ∣ ∣ w ∣ ∣ 2 l(w_1, w_2, b) + \frac{\lambda}{2n} ||\mathbf{w}||^2 l(w1,w2,b)+2nλ∣∣w∣∣2,其中 ∣ ∣ w ∣ ∣ 2 = w 1 2 + w 2 2 ||\mathbf{w}||^2=w_1^2 + w_2^2 ∣∣w∣∣2=w12+w22, 超参数 λ > 0 \lambda>0 λ>0叫做权重衰减因子

def l2_penalty(w): # 只惩罚权重
return (w**2).sum() / 2
l = loss(net(X, w, b), y) + lambd * l2_penalty(w) # L2正则化
l = l.sum()
w.grad.data.zero_()
b.grad.data.zero_()
l.backward()
dropout的实现: 丢弃法不改变输入的期望值
丢弃法也就是按一定的概率将某些地方的权重置为 0
def dropout(X, drop_prob): # X 是权重, drop_prob 是超参数
X = X.float()
assert 0 <= drop_prob <= 1
keep_prob = 1 - drop_prob # keep_prob 是保留的 drop_prob是丢弃概率
# 这种情况下把全部元素都丢弃
if keep_prob == 0:
return torch.zeros_like(X)
mask = (torch.rand(X.shape) < keep_prob).float() # 生成一个 0/1 矩阵
return mask * X / keep_prob # 除 keep_prob 是为了使 dropout 前后 X 的均值不变
二维卷积的实现
def corr2d(X, K): # 这里并没有设置 padding, stride,和多通道的运算
h, w = K.shape
Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (X[i: i + h, j: j + w] * K).sum()
return Y
池化层的实现
def pool2d(X, pool_k, mode='avg'): # 不考虑多通道等因素
p_h, p_k = pool_k.shape
h, w = X.shape
Y = torch.zeros([h - p_h + 1, w - p_k + 1]).float()
if mode == 'avg':
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
# Y[i][j] = X[i : i + p_h, j : j + p_k].sum() / (p_h * p_k)
Y[i][j] = X[i : i + p_h, j : j + p_k].mean()
if mode == 'max':
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i][j] = X[i : i + p_h, j : j + p_k].max()
return Y
X = torch.tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
pool_k = torch.ones(2, 2)
Y = pool2d(X, pool_k, 'max')
print(Y)
BN的实现
def batch_norm(is_training, X, gamma, beta, moving_mean, moving_var, eps, momentum):
# 判断当前模式是训练模式还是预测模式
if not is_training:
# 如果是在预测模式下,直接使用传入的移动平均所得的均值和方差
X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
else:
assert len(X.shape) in (2, 4)
if len(X.shape) == 2:
# 使用全连接层的情况,计算特征维上的均值和方差
mean = X.mean(dim=0)
var = ((X - mean) ** 2).mean(dim=0)
else:
# 使用二维卷积层的情况,计算通道维上(axis=1)的均值和方差。这里我们需要保持
# X的形状以便后面可以做广播运算
# 此题的X的形状是[C, B, H, W],X.mean(dim=0, keepdim=True)就是在求每个通道的均值,
#求完之后其实已经没有了btch的概念了,然后将每个通道的均值相加起来再求均值,
#所以就有了后面的mean(dim=2, keepdim=True)和emean(dim=3, keepdim=True)
mean = X.mean(dim=0, keepdim=True).mean(dim=2, keepdim=True).mean(dim=3, keepdim=True)
var = ((X - mean) ** 2).mean(dim=0, keepdim=True).mean(dim=2, keepdim=True).mean(dim=3, keepdim=True)
# 训练模式下用当前的均值和方差做标准化
X_hat = (X - mean) / torch.sqrt(var + eps)
# 更新移动平均的均值和方差
moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
moving_var = momentum * moving_var + (1.0 - momentum) * var
Y = gamma * X_hat + beta # 拉伸和偏移
return Y, moving_mean, moving_var