知识蒸馏(Knowledge Distillation)
0.Introduction
知识蒸馏(Knowledge Distillation,简记为 KD)是一种经典的模型压缩方法,核心思想是通过引导轻量化的学生模型“模仿”性能更好、结构更复杂的教师模型(或多模型的 ensemble),在不改变学生模型结构的情况下提高其性能。
2015 年 Hinton 团队提出的基于“响应”(response-based)的知识蒸馏技术(一般将该文算法称为 vanilla-KD [1])掀起了相关研究热潮,其后基于“特征”(feature-based)和基于“关系”(relation-based)的 KD 算法被陆续提出。
以上述三类蒸馏算法为基础,学术界不断涌现出致力于解决各特定问题、面向各特定场景的 KD 算法,如:
- 零训练数据情况下的 data-free KD;
- 教师模型权重更不更新的offline kd、 online KD、self KD;
- 面向检测、分割、自然语言处理等任务的 KD 算法等。
本文作为 KD 系列文章的头篇,将对 response-based、feature-based 和relation-based 这三类基础 KD 算法进行重点介绍。
1.Response-based KD
如下图所示,Response-based KD 算法以教师模型的分类预测结果为“目标知识”。具体来说,这里的分类预测结果指的是分类器最后一个全连接层的输出(称为 logits)。

与模型的最终输出相比,logits 没有经过 softmax 进行归一化,非目标类别对应的输出值尚未被抑制(假设教师模型 logits 中目标类别的对应值最高)。
在得到教师和学生的 logits 后,使用温度系数 T 分别对教师和学生的 logits 进行“软化”,进而计算二者的差异,具体的 loss 计算公式为:
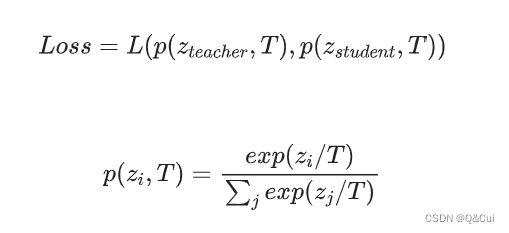
其中 z z z 为 logits, z i z_i zi 为 logtis 中第 i 个类别的对应值,损失函数 L() 一般使用 KL 散度计算差异。T 一般取大于 1 的整数值,此时目标类与非目标类的预测值差异减小,logits 被“软化”。相反地,T 小于 1 时会进一步拉大目标类与非目标类的数值差异,logtis 趋向于 one-hot。
由上可知,response-based KD 算法的知识提取和 loss 计算过程非常简洁,且 logits 本身具备较好理解的实际意义(模型判断当前样本为各类别的信心多少),因此研究者们将更多的注意力集中于 response-based KD 算法生效原因的解释。
1.1 Non-target class information
Vanilla-KD 认为:logits 提供的“软标签”信息相比于 one-hot 形式的真值标签(GT Label)有着更高的熵值,从而提供了更高的信息量以及数据之间更小的梯度差异。
文中举了一个 MNIST 数据集中的例子,对于某个手写数字 2,模型认为它是 3 的可能性为 1 0 − 6 10^{-6} 10−6,是 7 的可能性为 1 0 − 9 10^{-9} 10−9。其中便蕴含着“相比于 7 而言,当前的手写数字 2 与 3 更加近似”的信息,从而提供了当前样本与各非目标类别的类间关系信息。
但 logits 中的非目标类别的预测值通常相对过小(如上述预测为 3 的可能性仅为 1 0 − 6 10^{-6} 10−6),因此文中使用大于 1 的温度系数 T 降低类间得分差异(增大非目标类的预测值)。
DKD [3] 算法将 logits 信息拆分成目标类与非目标类两部分,进一步验证并得到 logits 中的非目标类别提供的信息是 response-based KD 起效的关键。
DKD 首先对原始 KD 损失进行拆解,从而解耦 KD 损失为 target class knowledge distillation (TCKD)和 non-target class knowledge distillation(NCKD)两部分:

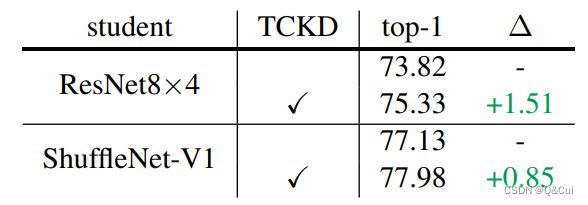
其中,TCKD 相当于目标类概率与(1-目标类概率)的二元预测损失,NCKD 则是不考虑目标类后的软标签蒸馏损失。之后对 TCKD 和 NCKD 的效果做消融,结果如下表所示,其中二者同时使用代表着原始 KD 损失。可以看到单独使用 NCKD 的效果非常好,甚至普遍优于完整的 KD 损失,而单独使用 TCKD 带来的性能提升不大甚至会降低训练效果。

那么对于目标类别的蒸馏部分是否应该直接去除呢?TCKD 在哪些任务场景中是有效的呢?
1.2 Difficulty transfer
DKD 认为教师 logits 中目标类预测值代表着教师模型对各样本的难度评估,举个例子,目标类别预测值为 0.99 的样本要比 0.75 的样本更简单。
当数据集较为简单时(如 1.1 节实验中使用的 CIFAR-100 数据集),教师模型 logtis 中目标类预测值均较高,样本难度信息的信息量很低时 TCKD 的效果会随之变差。
相反地,DKD 中相关实验表明,当经过数据增强、标签噪声化处理或任务本身较困难时,TCKD 的正面作用会更加明显。使用数据增强后的实验结果如下所示(使用 CIFAR-100 数据集),可以看到此时 TCKD 带来的正面作用明显。
无独有偶,BAN [4] 算法也对 logtis 中的目标类预测值进行了重点分析验证。
经过公式推导(详细推导过程见 BAN section 3.2)得到结论:教师 logits 中的目标类预测值相当于各样本的加权因子。
直接使用目标类预测值进行损失加权(Confidence Weighted by Teacher Max, CWTM)的结果如下所示(使用 CIFAR-100 数据集,指标为 test error),模型性能得到小幅提升。

需要说明的是:BAN 为级联自蒸馏算法,上表中 Teacher 即为学生模型;DKPP 为 dark knowledge with Permuted Predictions 的简写,具体做法为打乱非目标类的预测值,如原始为 [0.05, 0.2, 0.1, 0.6] 的 logits 打乱为 [0.2, 0.1, 0.05, 0.6]。
为什么 BAN 中使用打乱非目标类后的 logits 蒸馏(DKPP)依然有效,且在 DenseNet80-80 和 80-120 模型中得到了比 CWTM 更好的性能呢?
1.3 Label smoothing
原因在于,此时的软标签仍在起到类似标签平滑(label smoothing)的作用,从而提高了模型的泛化性。标签平滑是一种缓解模型过拟合问题的技术,它将 one-hot 形式的标签转换为如下形式,其中 为人为设定的超参数。
参考文献 [5] 认为:one-hot 形式的标签会鼓励模型将目标类别的概率预测为 1、非目标类别的概率预测为 0,从而导致 logtis 中目标类的值趋于无穷大。当训练数据质量较差(有偏分布明显)或数量较少时容易导致模型 over-confident。因此,为了提高模型的泛化能力,标签平滑将目标类的一部分标签值平均分给了非目标类。

可以发现,软标签与标签平滑有着异曲同工之妙,软标签在不经意间起到了标签平滑的作用。二者最主要的区别在于,软标签中非目标类的标签由教师给出,包含着类间关系信息。DKPP 打乱各类预测值后导致类间关系错乱,但仍起到了标签平滑的作用。
关于软标签损失与标签平滑损失的相同性、相异性等进一步关系分析详见参考文献 [6],同时,关于使用标签平滑训练后的教师能否用于知识蒸馏等问题的探究可见参考文献 [6]、[7]、[8]。
1.4 Quantifying
进一步地,response-based KD 在模型训练过程中起到了哪些正面影响(除了最终性能的提高)呢?
参考文献 [9] 从信息量化的角度对蒸馏过程进行了深入分析,该文章的深度分析可见第一作者的知乎回答,本文不再班门弄斧。文章中验证为真的三个假设为:
- 比起直接从数据学习,蒸馏算法往往使得深度神经网络(DNN)学到更多的知识;
- 比起直接从数据学习,蒸馏算法往往使得 DNN 更倾向于同时学到不同知识;
- 比起直接从数据学习,蒸馏算法往往使得 DNN 的优化方向更为稳定。
1.5 太长不看,直接看结论
如果你没有充足的时间浏览上面的各项论述,可以直接获取本节的结论:
- logits 中的非目标类信息是 response-based KD 起效的关键;
- 目标类信息传递的是教师模型对各样本“难度”的评估,数据噪声较大、任务困难的情况下,难度传递的作用更为明显;
- logits 相比于 one-hot label 而言,起到了类似标签平滑的作用,抑制了模型的 over-confidence 倾向,从而提高了模型泛化性;
- 从信息量化的角度来看,response-based KD 往往使得模型学到更多的知识、更倾向于同时学到不同的知识、优化方向更为稳定。
2.Feature-based KD
通常的知识蒸馏设置中,教师模型与学生模型的分类器(或检测器、解码器等)是一致的,二者的差异在于特征提取器(或称 backbone、encoder)能力的强弱。
对于深度神经网络而言,由输入数据抽象而来的特征的质量高低,很大程度上决定了模型性能的优劣。自然而然地,以教师模型特征提取器产生的中间层特征为学习对象的 feature-based KD 算法应运而生。
通常情况下,教师特征图的通道数大于学生通道数,二者无法完全对齐。为解决该问题,一般在学生特征图后接卷积层(或全连接层、由多层卷积构成的卷积模块等),将学生特征图通道数与教师特征图通道数对齐,从而实现特征点的一一对应。
损失函数计算公式如下所示,其中 f t f_t ft和 f s f_s fs分别代表教师和学生的特征图, ϕ t \phi_t ϕt和 ϕ s \phi_s ϕs分别代表对教师和学生特征的转换,从而实现二者的维度对齐, L F L_{F} LF 一般使用 L 2 L_2 L2损失。

2.1 Connector
实现特征对齐功能的模块(上面提到的 ϕ t \phi_t ϕt和 ϕ s \phi_s ϕs)是 feature-based KD 算法的核心模块(本文中称之为 connector),也是很多算法的重点研究对象。
如针对教师 connector 进行预训练的 Factor Transfer [11] 算法;以二值化形式筛选教师和学生原始特征的 AB [12] 算法;将特征值转换为注意力值的 AT [13] 算法等。
OFD [14] 对各相关算法进行总结,研究了多种蒸馏算法采用的特征位置、 connector 的构成、损失函数等因素对信息损失的影响,汇总表如下所示:

可以看到 connector 的样式多变,特征的选取位置也是多种多样,因此将上表中的算法集成到一个算法框架中看起来比较困难。那么,有没有一个算法库成功做到了这一点呢?
好消息!好消息!上面提到的 FitNets、Factor Transfer、AB、AT Loss(AT 算法与蒸馏最相关的损失计算部分)、OFD 等算法均被集成到了 MMRazor 算法库中,且核心模块 connector 被单独抽象出来作为可配置组件,非常便于大家进行“算法魔改”(如为 FitNets 算法配置上 Factor Transfer 的 connector 并计算 AT Loss)。
Recorder 机制更是实现了 function、method、model和parameter 等各类信息的“无痛”获取,大家不需要额外进行代码编写,只需要稍微更改 config 配置便可获取你想要的信息。
2.2 Summary
Feature-based KD相关的研究较多,本文不再进行深入讨论。稍作总结的话,该类别算法的核心关注点在于:
- 知识的定位(设计规则选出更为重要的教师特征,这一点在检测蒸馏算法中非常重要)
- 如何进行特征维度对齐、特征语义对齐、特征加权(connector 设计)
- 如何进行知识的高效传递(特征 fusion、loss 设计)
3.Relation-based KD
最后一个蒸馏基础算法是 relation-based KD,有的研究者会将该类别算法视为 feature-based KD 算法的一种。原因在于 relation-based KD 使用的信息也是模型特征,只不过计算的不是对应特征点之间的一对一差异,而是特征关系的差异。
relation-based KD 算法关心的重点是样本之间或特征层之间的关系,如分别构建教师和学生特征层之间关系矩阵的 FSP [15] 算法、分别构建相同 batch 内教师和学生各样本特征之间关系矩阵的 RKD [16] 算法,二者均计算关系矩阵的差异损失。

3.1 Relational Knowledge Distillation
以 RKD 算法为例,其核心思想如下图所示。RKD 认为关系是一种更 high-level 的信息,样本之间的关系差异信息优于单个样本在不同模型的表达差异信息,其中关系的差异同时包含两个样本之间的关系差异和三个样本之间的夹角差异。

将两两样本之间的关系组成的关系矩阵差异损失记为 L R K D − D L_{RKD-D} LRKD−D,计算公式如下所示:
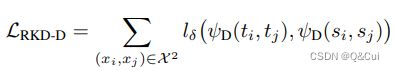
其中, l δ l_{\delta} lδ 为 Huber loss, ψ D ( t i , t j ) \psi_D(t_i,t_j) ψD(ti,tj) 计算的是欧式距离, t i t_i ti、 t j t_j tj 为不同样本的特征。将三个样本之间的夹角组成的角度关系矩阵差异损失记为 L R K D − A L_{RKD-A} LRKD−A ,计算公式如下所示:

其中, l δ l_{\delta} lδ 为 Huber loss, ψ A ( t i , t j , t k ) \psi_A(t_i,t_j,t_k) ψA(ti,tj,tk) 计算夹角余弦值,具体计算公式为:

3.2 Summary
近年来,relation-based KD 算法在分割任务中不断取得突破。同一张图像中,像素点之间的特征关系差异或区域之间的特征关系差异成为蒸馏分割模型的有效手段。但在检测任务中 relation-based KD 算法取得的成果较少。
一个可能的原因在于,构建高质量的关系矩阵需要大量的样本,分类和分割(以像素点或区域为样本)任务的样本数量足够大;而受限于存储空间大小等硬件因素,检测任务同一个 batch 中的前景目标(object)数量较少且存在低质量前景目标(被遮挡的、模糊的物体等),因此制约了样本间关系蒸馏在检测任务上的应用。
4.Conclusion
本文对知识蒸馏中的三类基础算法进行了浅薄的介绍,近年来的 KD 算法大多是依托于这三类基础算法进行的优化升级,相信本文对大家在知识蒸馏的进一步研究会有所帮助。
参考文献:
[1] Hinton G, Vinyals O, Dean J. Distilling the knowledge in a neural network[J]. arXiv preprint arXiv:1503.02531, 2015, 2(7).
[2] Gou J, Yu B, Maybank S J, et al. Knowledge distillation: A survey[J]. International Journal of Computer Vision, 2021, 129(6): 1789-1819.
[3] Zhao B, Cui Q, Song R, et al. Decoupled Knowledge Distillation[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022: 11953-11962.
[4] Furlanello T, Lipton Z, Tschannen M, et al. Born again neural networks[C]//International Conference on Machine Learning. PMLR, 2018: 1607-1616.
[5] Szegedy C, Vanhoucke V, Ioffe S, et al. Rethinking the inception architecture for computer vision[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 2818-2826.
[6] Shen Z, Liu Z, Xu D, et al. Is label smoothing truly incompatible with knowledge distillation: An empirical study[J]. arXiv preprint arXiv:2104.00676, 2021.
[7] Müller R, Kornblith S, Hinton G E. When does label smoothing help?[J]. Advances in neural information processing systems, 2019, 32.
[8] Chandrasegaran K, Tran N T, Zhao Y, et al. Revisiting Label Smoothing and Knowledge Distillation Compatibility: What was Missing?[C]//International Conference on Machine Learning. PMLR, 2022: 2890-2916.
[9] Zhang Q, Cheng X, Chen Y, et al. Quantifying the Knowledge in a DNN to Explain Knowledge Distillation for Classification[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022.
[10] Romero A, Ballas N, Kahou S E, et al. Fitnets: Hints for thin deep nets[J]. arXiv preprint arXiv:1412.6550, 2014.
[11] Kim J, Park S U, Kwak N. Paraphrasing complex network: Network compression via factor transfer[J]. Advances in neural information processing systems, 2018, 31.
[12] Heo B, Lee M, Yun S, et al. Knowledge transfer via distillation of activation boundaries formed by hidden neurons[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2019, 33(01): 3779-3787.
[13] Zagoruyko S, Komodakis N. Paying more attention to attention: Improving the performance of convolutional neural networks via attention transfer[J]. arXiv preprint arXiv:1612.03928, 2016.
[14] Heo B, Kim J, Yun S, et al. A comprehensive overhaul of feature distillation[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. 2019: 1921-1930.
[15] Yim J, Joo D, Bae J, et al. A gift from knowledge distillation: Fast optimization, network minimization and transfer learning[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2017: 4133-4141.
[16] Park W, Kim D, Lu Y, et al. Relational knowledge distillation[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2019: 3967-3976.
[17] OpenMMLab