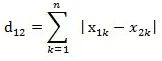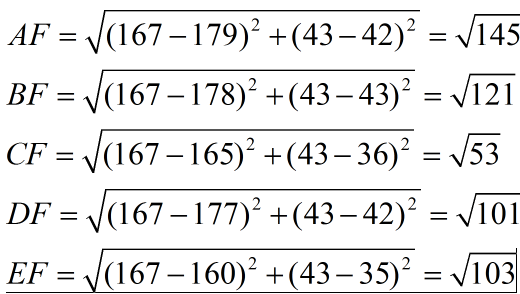(算法)K-NN邻近算法

（关注公zhong号：落叶归根的猪。获取资源，交个朋友～）

K - NEAREST NEIGHBORS

1. 基本概念与原理

k近邻算法是一种基本分类和回归方法。KNN算法非常简单且非常有效。KNN的模型表示是整个训练数据集。

该算法的思想是：一个样本与数据集中的k个样本最相似，如果这k个样本中的大多数属于某一个类别，则该样本也属于这个类别。

如上图所示，有两类不同的样本数据，分别用蓝色的小正方形和红色的小三角形表示，而图正中间的那个绿色的圆所标示的数据则是待分类的数据。这也就是我们的目的，来了一个新的数据点，我要得到它的类别是什么？

如果K=3，由于红色三角形所占比例为2/3，绿色圆将被赋予红色三角形那个类，如果K=5，由于蓝色四方形比例为3/5，因此绿色圆被赋予蓝色四方形类。

由此也说明了KNN算法的结果很大程度取决于K的选择。

 

2. k值的影响

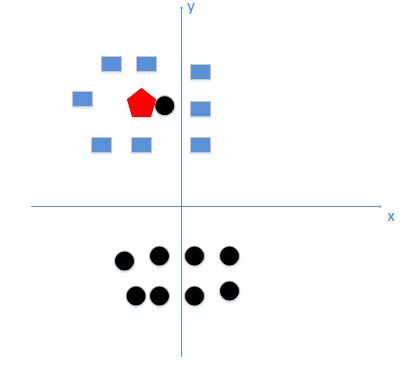
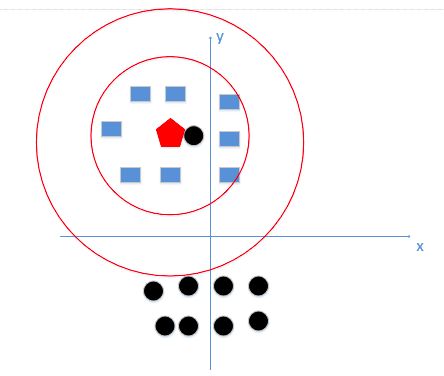
a. K值太小（k=1）：过拟合。如上图，若k太小，红色则被分类为黑色，由这个处理过程我们很容易能够感觉出问题了，如果k太小了，比如等于1，那么模型就太复杂了，我们很容易学习到噪声，也就非常容易判定为噪声类别，而在上图，如果，k大一点，k等于8，把长方形都包括进来，如下图：

b. K值太大（K=N，N为样本个数，很大）：模型过于简单。那么无论输入实例是什么，都将简单地预测它属于在训练实例中最多的类。这时，模型非常简单，因为根本就没有训练模型，直接用训练数据统计数据类别然后分类，找到最大即可，如下图：

我们统计了黑色圆形是8个，长方形个数是7个，那么哈哈，如果k=N，我就得出结论了，红色五边形是属于黑色圆形的

 

c. 理想K值：最理想的请看应该如下图（下图只有两个feature，但是真实情况是会有很多维）：

如何找到k值? —— 李航博士书上讲到，我们一般选取一个较小的数值，通常采取 交叉验证法来选取最优的k值。（也就是说，选取k值很重要的关键是实验调参，类似于神经网络选取多少层这种，通过调整超参数来得到一个较好的结果）

 

3. k值的确定：

在KNN中，通过计算对象间距离来作为各个对象之间的非相似性指标，避免了对象之间的匹配问题，在这里距离一般使用欧氏距离或曼哈顿距离：

多说一句：曼哈顿距离（Manhattan Distance）：

曼哈顿距离是由十九世纪的赫尔曼·闵可夫斯基所创词汇，是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。

图中红线代表曼哈顿距离，绿色代表欧氏距离，也就是直线距离，而蓝色和黄色代表等价的曼哈顿距离。曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离，即d（i，j）=|xi-xj|+|yi-yj|。对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离，因此，曼哈顿距离又称为出租车距离。

如在平面上，坐标（x1, y1）的i点与坐标（x2, y2）的j点的曼哈顿距离为：

d(i,j)=|X1-X2|+|Y1-Y2|

二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离

两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的曼哈顿距离

曼哈顿距离的一个优点是计算速度快

（欧式距离不多说了，是我们以前初中学习的两点距离）

 

4. 特征归一化

为什么要特征归一化？—— 比如我们预测房价，predicrtion是price，但是feature有很多，价格可以是几千几万（一个feature），另一个feature可以是面积，几十几百平方。所以数据不同feature之间需要正规化。

举例如下，我用一个人身高(cm)与脚码（尺码）大小来作为特征值，类别为男性或者女性。我们现在如果有5个训练样本，分布如下：

A [(179,42),男] B [(178,43),男] C [(165,36)女] D [(177,42),男] E [(160,35),女]

通过上述训练样本，我们看出问题了吗？

很容易看到第一维身高特征是第二维脚码特征的4倍左右，那么在进行距离度量的时候，我们就会偏向于第一维特征。这样造成俩个特征并不是等价重要的，最终可能会导致距离计算错误，从而导致预测错误。口说无凭，举例如下：

现在我来了一个测试样本 F(167,43)，让我们来预测他是男性还是女性，我们采取k=3来预测。

下面我们用欧式距离分别算出F离训练样本的欧式距离，然后选取最近的3个，多数类别就是我们最终的结果，计算如下：

由计算可以得到，最近的前三个分别是C,D,E三个样本，那么由C,E为女性，D为男性，女性多于男性得到我们要预测的结果为女性。

这样问题就来了，一个女性的脚43码的可能性，远远小于男性脚43码的可能性，那么为什么算法还是会预测F为女性呢？那是因为由于各个特征量纲的不同，在这里导致了身高的重要性已经远远大于脚码了，这是不客观的。所以我们应该让每个特征都是同等重要的！这也是我们要归一化的原因！归一化公式如下：

5. 总结：

1. 算法的核心思想是，即是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例，这K个实例的多数属于某个类，就把该输入实例分类到这个类中。更通俗说一遍算法的过程，来了一个新的输入实例，我们算出该实例与每一个训练点的距离（这里的复杂度为0(n)比较大，所以引出了下文的kd树等结构），然后找到前k个，这k个哪个类别数最多，我们就判断新的输入实例就是哪类！

2.与该实例最近邻的k个实例，这个最近邻的定义是通过不同距离函数来定义，我们最常用的是欧式距离。

3.为了保证每个特征同等重要性，我们这里对每个特征进行归一化。

4.k值的选取，既不能太大，也不能太小，何值为最好，需要实验调整参数确定！