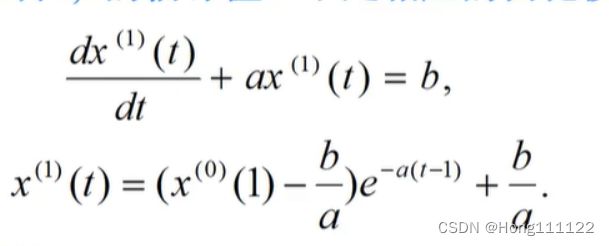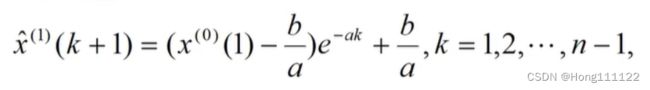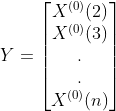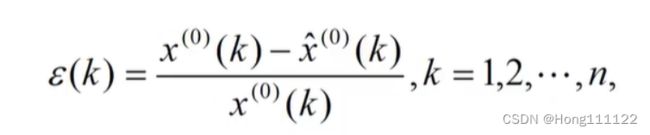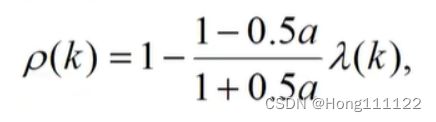数学建模：预测性模型学习——灰色预测模型（GM（1，1）模型）
目录
前言
一、模型实现
1、流程介绍
2、灰色生成
1.累加生成算子
2.均值生成算子
3.可行性分析（级比检验）
4.建立GM(1,1)模型
1.数据预处理：
2.建立模型：
3.构造数据矩阵B及数据向量Y：
5.精度检验
二、案例分析
总结
前言
简要介绍灰色预测模型，并采用matlab对具体案例进行分析，后续会继续补充
一、模型实现
1、流程介绍
- 灰色生成新算子
- 可行性分析
- 建立GM（1，1）模型
- 精度检验
2、灰色生成
简单而言，灰色生成新算子的目的是将无序的序列弱化其随机性，转化为有序的序列展示其中规律并进行分析。常见的生成算子有以下几种：
- 1.累加生成算子（AGO）
- 2.逆累加生成算子（IAGO）
- 3.均值生成算子（MEAN)
- 4.级比生成算子
1.累加生成算子
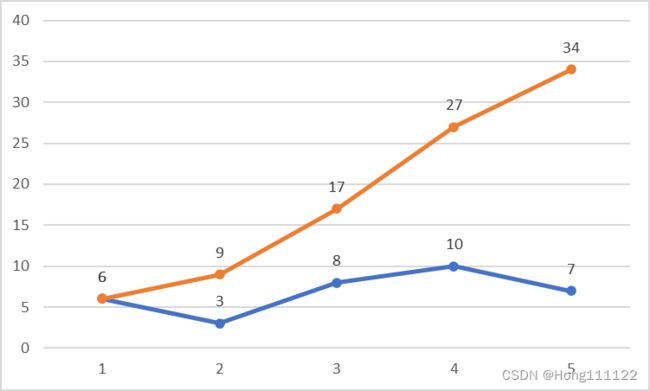
新序列与旧序列折线图如下，可见新序列将原本无规律的序列转换为了有明显规律、递增的序列：
2.均值生成算子
即对累加生成算子相邻两项求均值，以上述例子为例：
![Z^{(1)}(k)=1/2\left [ X^{(1)}(k-1)+X^{(1)}(k) \right ] \, \, \, \, \, \, k=2,3...](http://img.e-com-net.com/image/info8/bec6267a8521484096e7ac073786de4d.gif){kind=small}
3.可行性分析（级比检验）
先对原始序列每两项求比值，即级比，以上述例子为例：
计算
的级比： 
若级比满足：
则新算子
或
可建立GM(1,1)模型
ps：有个条件，必须是非负的，如果有负数项，则在后加上一个正数a，使得 、或均为非负再进行后续操作。
4.建立GM(1,1)模型
1.数据预处理：
先行假设原序列
通过级比检验，
以均值生成算子为例：
新序列： 
ps：同样的，如果级比检验不通过，也可在后加上一个正数a，使得所有级比都在可容范围内。
2.建立模型：
1.原始形式：
,目的：将a，b求出
2.用回归分析估计a，b，相应的白化微分方程及其解为：
由此得到预测值：
原序列预测值：
3.构造数据矩阵B及数据向量Y：
令 
，求解上述微分方程得 
求出a，b代入上述预测值便拟合出了一个预测值函数
5.精度检验
残差检验：
若对所有残差绝对值小于0.1则认为达到较高要求；小于0.2则达到一般要求；
级比偏差值检验：
若对所有级比偏差值绝对值小于0.1则认为达到较高要求；小于0.2则达到一般要求；
二、案例分析
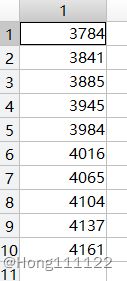
根据福建省过去十年常住人口数量预测未来n年常住人口数量
2010--2020年数据为：[3693,3784,3841,3885,3945,3984,4016,4065,4104,4137,4161] 万人
1.级比检验：
满足级比检验区间：（0.8574，1.1663）
通过matlab算得级比为：
均通过级比检验
代码：
%级比检验通过
check = [];
for k = 2:n
lambda(k) = data(k-1)/data(k);
if (exp(-2/(n+1))2.生成算子：
累加生成算子：
均值生成算子:
代码：
%累加生成算子
X1 = cumsum(data);
for i=2:n
z(i) = 0.5*(X1(i-1)+X1(i));
end3.求数据矩阵B及数据向量Y
B： Y：
代码：
%数据矩阵B及数据向量Y
Y = data(2:n)';
B = [-z(2:n)',ones(n-1,1)];
u = (B'*B)\B'*Y;
a = u(1,1);
b = u(2,1);4.生成预测值
和
：
：
代码：
%预测值
f_X1 = [];
f_X0 = [];
for k=1:n-1
f_X1(1)=data(1);
f_X1(k+1) = (data(1)-b/a)*exp(-a*k) + b/a;
end
for k=2:n
f_X0(1)=data(1);
f_X0(k)=f_X1(k)-f_X1(k-1);
end5.残差检验和级比偏差值检验：
残差检验：
级比偏差值检验：
均小于0.1，证明模型精确度高，可用于预测
代码：
%残差检验&级比偏差值检验
for k=1:n-1
sigma(k)=abs((data(k)-f_f_X0(k))/data(k));
rho(k+1)=abs(1-((1-0.5*a)*lambda(k+1))/(1+0.5*a));
end
6.完整代码如下，需要往下预测多少可自行input：
%10至20年数据，21年数据为4219
data = [3693,3784,3841,3885,3945,3984,4016,4065,4104,4137,4161];
n = length(data);
%级比检验通过
check = [];
for k = 2:n
lambda(k) = data(k-1)/data(k);
if (exp(-2/(n+1))结果得21年常住人口为4228万人，与真实数据4219接近。
三、分析总结