第十三届蓝桥杯 C++ B 组省赛 G 题———积木画(AC)
目录
- 1.积木画
-
- 1.题目描述
- 2.输入格式
- 3.输出格式
- 4.样例输入
- 5.样例输出
- 6.样例说明
- 7.数据范围
- 8.原题链接
- 2.解题思路
- AC_code
1.积木画
1.题目描述
小明最近迷上了积木画, 有这么两种类型的积木, 分别为 I I I 型(大小为 2 个单位面积) 和 L L L 型 (大小为 3 个单位面积):
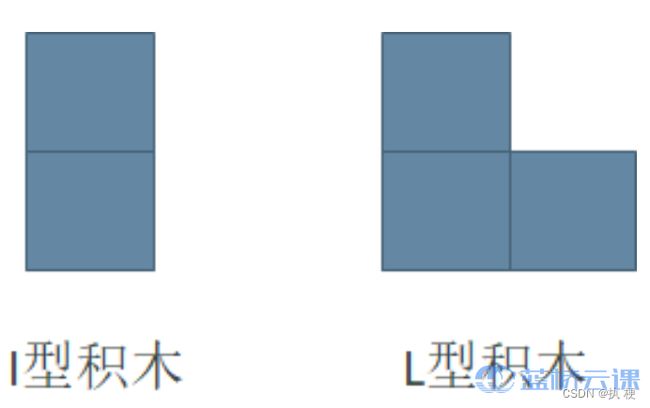
同时, 小明有一块面积大小为 2 × N 2 \times N 2×N 的画布, 画布由 2 × N 2 \times N 2×N 个 1 × 1 1 \times 1 1×1 区域构 成。小明需要用以上两种积木将画布拼满, 他想知道总共有多少种不同的方式? 积木可以任意旋转, 且画布的方向固定。
2.输入格式
输入一个整数 N N N,表示画布大小。
3.输出格式
输出一个整数表示答案。由于答案可能很大,所以输出其对 1000000007 取模后的值。
4.样例输入
3
5.样例输出
5
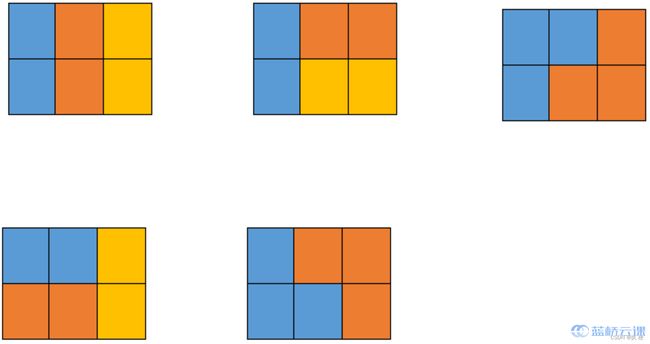
6.样例说明
五种情况如下图所示,颜色只是为了标识不同的积木:
7.数据范围
1 ≤ N ≤ 1 0 7 1≤N≤10^7 1≤N≤107
8.原题链接
积木画
2.解题思路
比较简单的状态压缩 d p dp dp 的模型,虽然 N N N 很大,但总共只有两行,所以只需要考虑结尾的插入情况即可。
定义 f [ i ] [ j ] f[i][j] f[i][j] 为已经排好了前 i − 1 i-1 i−1 列,且第 i i i 列的状态为 j j j 的方案数。当 j j j 为 0 时表示第 i i i 列上面和下面均未摆放积。为 1 时表示上面未摆,下面摆放了积木。当为 2 时表示上面摆了,下面未摆的情况,当为 3 时表示上下均摆好了积木的情况。
从定义可知最终答案为 f [ n ] [ 3 ] f[n][3] f[n][3]
考虑如何进行初始化,当 n n n 为0时,可以视为完全摆好的情况,则 f [ 0 ] [ 3 ] = 1 f[0][3]=1 f[0][3]=1,当 n n n 为 1 时,只有一种摆法,则 f [ 1 ] [ 3 ] = 1 f[1][3]=1 f[1][3]=1。
接下来考虑如何进行状态转移:
首先考虑 f [ i ] [ 0 ] f[i][0] f[i][0] ,因为0表示上下都未摆放积木,而状态定义就要求了前 i − 1 i-1 i−1列已经摆好,则转移方程:
f [ i ] [ 0 ] = f [ i − 1 ] [ 3 ] f[i][0]=f[i-1][3] f[i][0]=f[i−1][3]
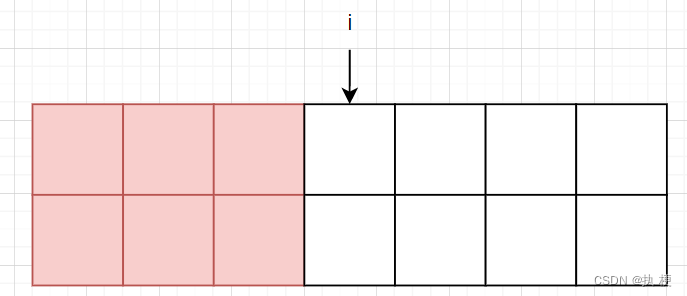
然后考虑 f [ i − 1 ] [ 1 ] f[i-1][1] f[i−1][1]如何转移:
1表示我们第 i i i 列是下面摆放了上面未摆放,也就是下面突出了一格,我们考虑如何才会产生这样的效果:
当这样摆放时可以得到,但转移时不应该从 i − 1 i-1 i−1 列转移,而应该是从 f [ i − 2 ] [ 3 ] f[i-2][3] f[i−2][3] 转移。
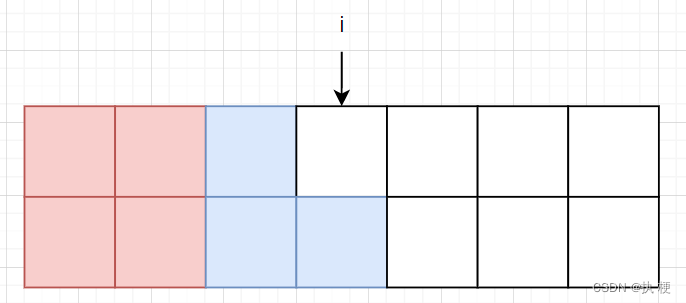
除此之外我们还可以像下面这样插入,这样我们可以从 f [ i − 1 ] [ 2 ] f[i-1][2] f[i−1][2]转移过来。
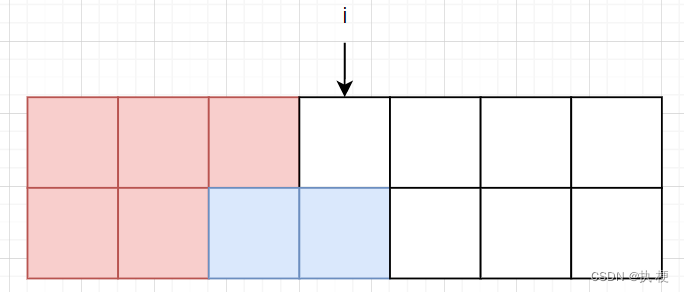
综上我们有两种情况可以得到 f [ i ] [ 1 ] f[i][1] f[i][1],转移方程为:
f [ i ] [ 1 ] = ( f [ i − 1 ] [ 0 ] + f [ i − 1 ] [ 2 ] ) f[i][1] = (f[i - 1][0] + f[i - 1][2]) f[i][1]=(f[i−1][0]+f[i−1][2])
分析 f [ i ] [ 2 ] f[i][2] f[i][2]其实和 f [ i ] [ 1 ] f[i][1] f[i][1]同理,反过来就行,有如下两种插入情况:
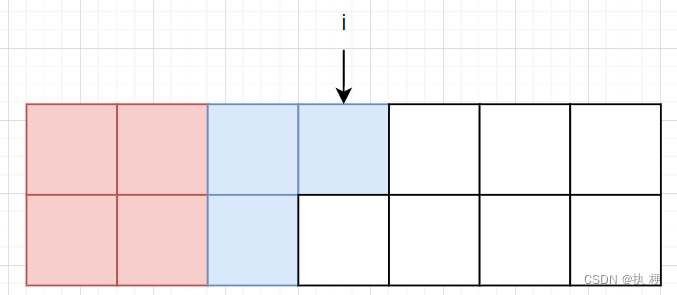
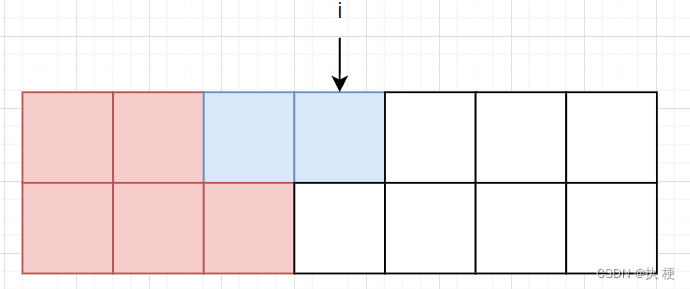
那么转移方程则为:
f [ i ] [ 2 ] = ( f [ i − 1 ] [ 0 ] + f [ i − 1 ] [ 1 ] ) f[i][2] = (f[i - 1][0] + f[i - 1][1]) f[i][2]=(f[i−1][0]+f[i−1][1])
最后考虑 f [ i ] [ 3 ] f[i][3] f[i][3]如何转移,这个转移的情况比较多,直接上图大家就能看懂了:
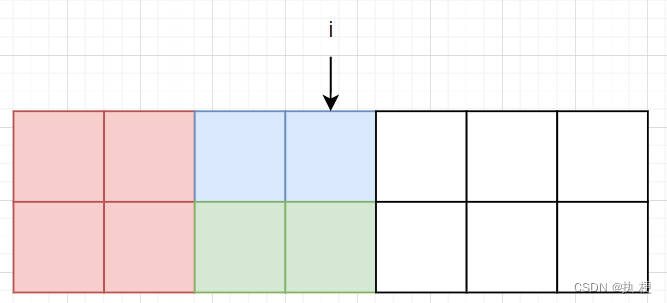
横着插两块,从 f [ i − 2 ] [ 3 ] f[i-2][3] f[i−2][3]转移
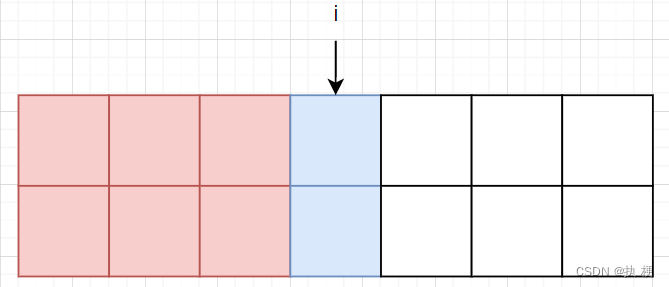
可以从 f [ i − 1 ] [ 3 ] f[i-1][3] f[i−1][3]转移
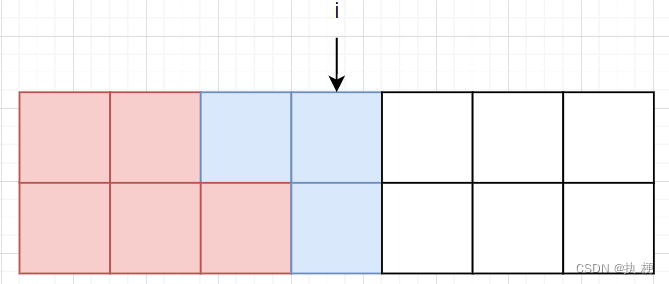
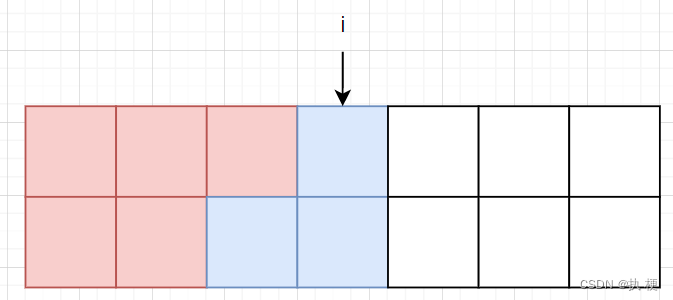
可以从 f [ i − 1 ] [ 1 ] f[i-1][1] f[i−1][1]和 f [ i − 1 ] [ 2 ] f[i-1][2] f[i−1][2]转移,综上:
f [ i ] [ 3 ] = ( f [ i − 2 ] [ 3 ] + f [ i − 1 ] [ 3 ] + f [ i − 1 ] [ 2 ] + f [ i − 1 ] [ 1 ] ) f[i][3] = (f[i - 2][3] + f[i - 1][3] + f[i - 1][2] + f[i - 1][1]) f[i][3]=(f[i−2][3]+f[i−1][3]+f[i−1][2]+f[i−1][1])
AC_code
#include