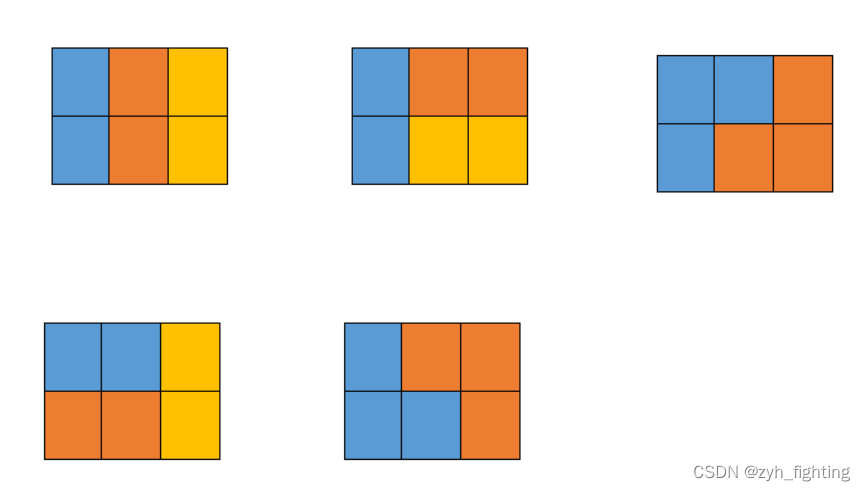【第十三届蓝桥杯】省赛C/C++ B组 题目+题解
目录
A: 九进制转十进制
B: 顺子日期
C: 刷题统计
D: 修剪灌木
E: X 进制减法
F: 统计子矩阵
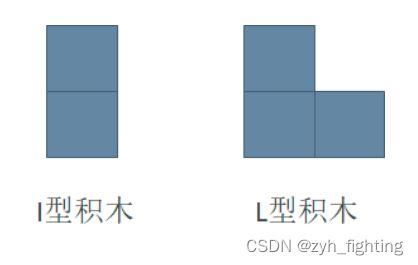
G: 积木画
H: 扫雷
I: 李白打酒加强版
J: 砍竹子
A: 九进制转十进制
本题总分： 5 分
【问题描述】
九进制正整数 (2022) 
转换成十进制等于多少？
转换成十进制等于多少？
2 + 2 * 9 + 2 *
= 1478
1478
B: 顺子日期
本题总分： 5 分
【问题描述】
小明特别喜欢顺子。顺子指的就是连续的三个数字： 123 、 456 等。顺子日 期指的就是在日期的 yyyymmdd 表示法中，存在任意连续的三位数是一个顺 子的日期。例如 20220123 就是一个顺子日期，因为它出现了一个顺子： 123 ； 而 20221023 则不是一个顺子日期，它一个顺子也没有。小明想知道在整个 2022 年份中，一共有多少个顺子日期。
该题有异议如果012算顺子，答案为 140120
0121
0122
0123
0124
0125
0126
0127
0128
0129
1012
1123
1230
1231
如果012不算顺子，答案为 40123
1123
1230
1231
C: 刷题统计
时间限制 : 1.0s
内存限制 : 256.0MB
本题总分： 10 分
【问题描述】
小明决定从下周一开始努力刷题准备蓝桥杯竞赛。他计划周一至周五每天
做 a 道题目，周六和周日每天做 b 道题目。请你帮小明计算，按照计划他将在 第几天实现做题数大于等于 n 题？
【输入格式】
输入一行包含三个整数 a , b 和 n .
【输出格式】
输出一个整数代表天数。
【样例输入】
10 20 99 【样例输出】
8 【评测用例规模与约定】
对于 50 % 的评测用例， 1 ≤ a , b , n ≤ 
.
.
对于 100 % 的评测用例， 1 ≤ a , b , n ≤ 
.
.
算法标签：模拟
看n的取值范围，不能暴力枚举，会TLE。利用每七天一循环。
代码：
#include
#include
using namespace std;
typedef long long LL;
int main()
{
LL a, b, n;
cin >> a >> b >> n;
LL s = 5 * a + 2 * b;
LL res = n / s * 7;
n %= s;
LL d[] = {a, a, a, a, a, b, b};
for(int i = 0; n > 0; i++)
{
n -= d[i];
res++;
}
cout << res << endl;
return 0;
} D: 修剪灌木
时间限制 : 1.0s
内存限制 : 256.0MB
本题总分： 10 分
【问题描述】
爱丽丝要完成一项修剪灌木的工作。
有 N 棵灌木整齐的从左到右排成一排。爱丽丝在每天傍晚会修剪一棵灌
木，让灌木的高度变为 0 厘米。爱丽丝修剪灌木的顺序是从最左侧的灌木开始， 每天向右修剪一棵灌木。当修剪了最右侧的灌木后，她会调转方向，下一天开 始向左修剪灌木。直到修剪了最左的灌木后再次调转方向。然后如此循环往复。
灌木每天从早上到傍晚会长高 1 厘米，而其余时间不会长高。在第一天的
早晨，所有灌木的高度都是 0 厘米。爱丽丝想知道每棵灌木最高长到多高。
【输入格式】
一个正整数 N ，含义如题面所述。
【输出格式】
输出 N 行，每行一个整数，第行表示从左到右第 i 棵树最高能长到多高。
【样例输入】
3 【样例输出】
4
2
4 【评测用例规模与约定】
对于 30 % 的数据， N ≤ 10 .
对于 100 % 的数据， 1 < N ≤ 10000.
算法标签：模拟
从第i棵树开始：
向右走：第i棵树的最大高度为：2(n - i);
向左走：第i棵树的最大高度为：2(i - 1).
两值取max即为最大高度
代码：
#include
#include
using namespace std;
int main()
{
int n;
cin >> n;
for(int i = 1; i <= n; i++)
{
cout << max(2 * (i - 1), 2 * (n - i)) << endl;
}
return 0;
} E: X 进制减法
时间限制 : 1.0s
内存限制 : 256.0MB
本题总分： 15 分
【问题描述】
进制规定了数字在数位上逢几进一。
X 进制是一种很神奇的进制，因为其每一数位的进制并不固定！例如说某
种 X 进制数，最低数位为二进制，第二数位为十进制，第三数位为八进制，则 X 进制数 321 转换为十进制数为 65 。
现在有两个 X 进制表示的整数 A 和 B ，但是其具体每一数位的进制还不确
定，只知道 A 和 B 是同一进制规则，且每一数位最高为 N 进制，最低为二进 制。请你算出 A − B 的结果最小可能是多少。
请注意，你需要保证 A 和 B 在 X 进制下都是合法的，即每一数位上的数
字要小于其进制。
【输入格式】
第一行一个正整数 N ，含义如题面所述。
第二行一个正整数 M a ，表示 X 进制数 A 的位数。
第三行 M a 个用空格分开的整数，表示 X 进制数 A 按从高位到低位顺序各
个数位上的数字在十进制下的表示。
第四行一个正整数 M b ，表示 X 进制数 B 的位数。
第五行 M b 个用空格分开的整数，表示 X 进制数 B 按从高位到低位顺序各
个数位上的数字在十进制下的表示。
请注意，输入中的所有数字都是十进制的。
【输出格式】
输出一行一个整数，表示 X 进制数 A − B 的结果的最小可能值转换为十进
制后再模 1000000007 的结果。
【样例输入】
11
3
10 4 0
3
1 2 0 【样例输出】
94 【样例说明】
当进制为：最低位 2 进制，第二数位 5 进制，第三数位 11 进制时，减法
得到的差最小。此时 A 在十进制下是 108 ， B 在十进制下是 14 ，差值是 94 。
【评测用例规模与约定】
对于 30 % 的数据， N ≤ 10; M a , M b ≤ 8 .
对于 100 % 的数据， 2 ≤ N ≤ 1000; 1 ≤ M a , M b ≤ 100000; A ≥ B .
算法标签：贪心
将321转换为65过程：
3 * 10 * 2 + 2 * 2 + 1 = 65。
差值最小，是 a，b的每位数的进制最低。
欲使a-b最小，只需使得各位数字取得合法范围内的最小进制即可，具体做法就是对a和b中相同数位的数字取max(a[i] + 1, b[i] + 1，2).
+1是因为：比如八进制， 最大数字为7， 求的是进制所以要+1.
因为a >= b, b的位数如果比a少，要在高位上补0，从低位向高位存取
代码：
#include
#include
using namespace std;
typedef long long LL;
const int N = 100010, mod = 1000000007;
int n, ma, mb, m;
int a[N], b[N];
int g[N]; // 各位进制
LL w[N];
LL A, B;
int main()
{
cin >> n;
cin >> ma;
for(int i = ma - 1; i >= 0; i--) cin >> a[i];
cin >> mb;
for(int i = mb - 1; i >= 0; i--) cin >> b[i];
int m = max(ma, mb);
// 确定各位进制
for(int i = m - 1; i >= 0; i--)
g[i] = max({a[i] + 1, b[i] + 1, 2});
// 计算各位权重
w[0] = 1;
for(int i = 1; i <= m - 1; i++)
w[i] = w[i - 1] * g[i - 1] % mod;
// 计算A
for(int i = m - 1; i >= 0; i--)
A = (A + a[i] * w[i]) % mod;
// 计算B
for(int i = m - 1; i >= 0; i--)
B = (B + b[i] * w[i]) % mod;
LL res = (A - B + mod) % mod;
cout << res << endl;
return 0;
} 优化后代码：
#include
#include
using namespace std;
typedef long long LL;
const int N = 100010, mod = 1000000007;
int n, ma, mb, m;
int a[N], b[N];
int main()
{
cin >> n;
cin >> ma;
for(int i = ma - 1; i >= 0; i--) cin >> a[i];
cin >> mb;
for(int i = mb - 1; i >= 0; i--) cin >> b[i];
int m = max(ma, mb);
int res = 0;
for(int i = m - 1; i >= 0; i--) // A - B
res = (res * (LL)max({a[i] + 1, b[i] + 1, 2}) + a[i] - b[i]) % mod;
cout << res << endl;
return 0;
} F: 统计子矩阵
时间限制 : 1.0s
内存限制 : 256.0MB
本题总分： 15 分
【问题描述】
给定一个 N × M 的矩阵 A ，请你统计有多少个子矩阵 ( 最小 1 × 1 ，最大
N × M ) 满足子矩阵中所有数的和不超过给定的整数 K ?
【输入格式】
第一行包含三个整数 N , M 和 K .
之后 N 行每行包含 M 个整数，代表矩阵 A .
【输出格式】
一个整数代表答案。
【样例输入】
3 4 10
1 2 3 4
5 6 7 8
9 10 11 12 【样例输出】
19 【样例说明】
满足条件的子矩阵一共有 19 ，包含：
大小为 1 × 1 的有 10 个。
大小为 1 × 2 的有 3 个。
大小为 1 × 3 的有 2 个。
大小为 1 × 4 的有 1 个。
大小为 2 × 1 的有 3 个。
【评测用例规模与约定】
对于 30 % 的数据， N , M ≤ 20 .
对于 70 % 的数据， N , M ≤ 100 .
对于 100 % 的数据， 1 ≤ N , M ≤ 500; 0 ≤ A i j ≤ 1000; 1 ≤ K ≤ 250000000 .
算法标签：前缀和，双指针
直接用二维前缀和枚举，O(
)会超时，所以用双指针优化。
把每一列看成一个元素， 把二维问题变成一维问题，
代码：
#include
#include
using namespace std;
typedef long long LL;
const int N = 505;
int n, m, k;
int s[N][N]; // 每一列上的前缀和
int main()
{
cin >> n >> m >> k;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
{
cin >> s[i][j];
s[i][j] += s[i - 1][j];
}
LL res = 0;
for(int i = 1; i <= n; i++) // i, j表示上下边界， l，r表示左右边界
for(int j = i; j <= n; j++)
for(int l = 1, r = 1, sum = 0; r <= m; r++)
{
sum += s[j][r] - s[i - 1][r];
while(sum > k)
{
sum -= s[j][l] - s[i - 1][l];
l++;
}
res += r - l + 1;
}
cout << res << endl;
return 0;
} G: 积木画
时间限制 : 1.0s
内存限制 : 256.0MB
本题总分： 20 分
【问题描述】
小明最近迷上了积木画，有这么两种类型的积木，分别为 I 型（大小为 2
个单位面积）和 L 型（大小为 3 个单位面积）：
同时，小明有一块面积大小为 2 × N 的画布，画布由 2 × N 个 1 × 1 区域构成。小明需要用以上两种积木将画布拼满，他想知道总共有多少种不同的方式？
积木可以任意旋转，且画布的方向固定。
【输入格式】
输入一个整数 N ，表示画布大小。
【输出格式】
输出一个整数表示答案。由于答案可能很大，所以输出其对 1000000007 取 模后的值
【样例输入】
3 【样例输出】
5 【样例说明】
五种情况如下图所示，颜色只是为了标识不同的积木：
【评测用例规模与约定】
对于所有测试用例， 1 ≤ N ≤ 10000000 .
算法标签：状态压缩DP
f(i, j)表示已经操作完前i - 1列，且第i列的状态为j的所有方案的集合
#include
#include
using namespace std;
const int N = 1e7 + 10, mod = 1e9 + 7;
int n;
int g[4][4] = {
{1, 1, 1, 1},
{0, 0, 1, 1},
{0, 1, 0, 1},
{1, 0, 0, 0},
};
int f[N][4];
int main()
{
cin >> n;
f[1][0] = 1;
for(int i = 1; i <= n; i++)
for(int j = 0; j < 4; j++)
for(int k = 0; k < 4; k++)
f[i + 1][k] = (f[i + 1][k] + f[i][j] * g[j][k]) % mod;
cout << f[n + 1][0] << endl;
return 0;
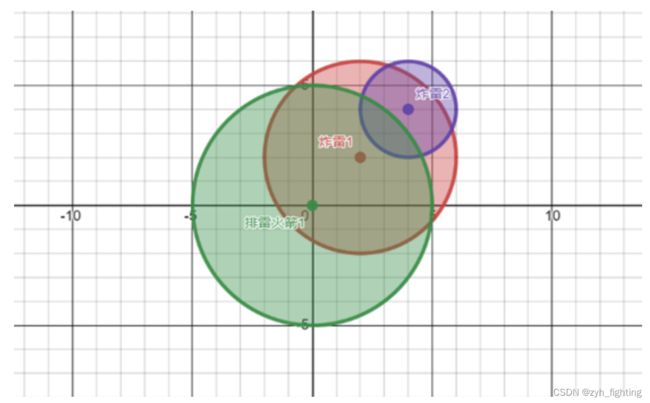
} H: 扫雷
时间限制 : 1.0s
内存限制 : 256.0MB
本题总分： 20 分
【问题描述】
小明最近迷上了一款名为《扫雷》的游戏。其中有一个关卡的任务如下，
在一个二维平面上放置着 n 个炸雷，第 i 个炸雷 ( x i ， y i， r i ) 表示在坐标 ( x i， y i ) 处 存在一个炸雷，它的爆炸范围是以半径为 r i 的一个圆。
为了顺利通过这片土地，需要玩家进行排雷。玩家可以发射 m 个排雷火
箭，小明已经规划好了每个排雷火箭的发射方向，第 j 个排雷火箭 ( x j ， y j ， r j ) 表 示这个排雷火箭将会在 ( x j ， y j ) 处爆炸，它的爆炸范围是以半径为 r j 的一个圆，在其爆炸范围内的炸雷会被引爆。同时，当炸雷被引爆时，在其爆炸范围内的 炸雷也会被引爆。现在小明想知道他这次共引爆了几颗炸雷？
你可以把炸雷和排雷火箭都视为平面上的一个点。一个点处可以存在多个
炸雷和排雷火箭。当炸雷位于爆炸范围的边界上时也会被引爆。
【输入格式】
输入的第一行包含两个整数 n 、 m .
接下来的 n 行，每行三个整数 x i , y i , r i ，表示一个炸雷的信息。
再接下来的 m 行，每行三个整数 x j , y j , r j ，表示一个排雷火箭的信息。
【输出格式】
输出一个整数表示答案。
【样例输入】
2 1
2 2 4
4 4 2
0 0 5 【样例输出】
2 【样例说明】
示例图如下，排雷火箭 1 覆盖了炸雷 1 ，所以炸雷 1 被排除；炸雷 1 又覆
盖了炸雷 2 ，所以炸雷 2 也被排除。
【评测用例规模与约定】
对于 40 % 的评测用例： 0 ≤ x , y ≤ 
, 0 ≤ n , m ≤ 
, 1 ≤ r ≤ 10 .
, 0 ≤ n , m ≤ , 1 ≤ r ≤ 10 .
对于 100 % 的评测用例： 0 ≤ x , y ≤ , 0 ≤ n , m ≤ 5 × 
, 1 ≤ r ≤ 10 .
, 0 ≤ n , m ≤ 5 × , 1 ≤ r ≤ 10 .
算法标签：图的遍历，DFS， BFS， 哈希
需要构建有向图，对于每个地雷，只需遍历周围一圈r内坐标即可，由坐标点知道是否有地雷，需要用到哈希表， 该题需要手写哈希表。
代码：
#include
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 50010, M = 999997;
int n, m;
struct circle
{
int x, y, r;
}cir[N];
LL h[M];
int id[M];
bool st[M];
LL get_key(int x, int y) // 得到每个坐标的哈希值
{
return x * 1000000001ll + y;
}
int find(int x, int y) // 找到该坐标在哈希数组中存储下标t
{
LL key = get_key(x, y);
int t = (key % M + M) % M;
while(h[t] != -1 && h[t] != key) //如果该位置已被占用并且不等于要求的哈希值
if(++t == M)
t = 0;
return t;
}
int sqr(int x)
{
return x * x;
}
void dfs(int x, int y, int r)
{
st[find(x, y)] = true;
for(int i = x - r; i <= x + r; i++)
for(int j = y - r; j <= y + r; j++)
if(sqr(i - x) + sqr(j - y) <= sqr(r))
{
int t = find(i, j);
if(id[t] && !st[t])
dfs(i, j, cir[id[t]].r);
}
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
for(int i = 1; i <= n; i++)
{
int x, y, r;
scanf("%d%d%d", &x, &y, &r);
cir[i] = {x, y, r};
int t = find(x, y);
if(h[t] == -1) h[t] = get_key(x, y);
// 如果该id没有没占用，或者找到了同一坐标点更大半径的地雷
if(!id[t] || cir[id[t]].r < r)
id[t] = i;
}
while(m--)
{
int x, y, r;
scanf("%d%d%d", &x, &y, &r);
// 枚举周围的正方形区域，然后判断是否在圆内
for(int i = x - r; i <= x + r; i++)
for(int j = y - r; j <= y + r; j++)
if(sqr(i - x) + sqr(j - y) <= sqr(r))
{
int t = find(i, j);
if(id[t] && !st[t])
dfs(i, j, cir[id[t]].r);
}
}
int res = 0;
for(int i = 1; i <= n; i++)
if(st[find(cir[i].x, cir[i].y)])
res++;
cout << res << endl;
return 0;
} I: 李白打酒加强版
时间限制 : 1.0s
内存限制 : 256.0MB
本题总分： 25 分
【问题描述】
话说大诗人李白，一生好饮。幸好他从不开车。
一天，他提着酒壶，从家里出来，酒壶中有酒 2 斗。他边走边唱：
无事街上走，提壶去打酒。
逢店加一倍，遇花喝一斗。
这一路上，他一共遇到店 N 次，遇到花 M 次。已知最后一次遇到的是花， 他正好把酒喝光了。
请你计算李白这一路遇到店和花的顺序，有多少种不同的可能？
注意：壶里没酒 ( 0 斗 ) 时遇店是合法的，加倍后还是没酒；但是没酒时遇
花是不合法的。
【输入格式】
第一行包含两个整数 N 和 M .
【输出格式】
输出一个整数表示答案。由于答案可能很大，输出模 1000000007 的结果。
【样例输入】
5 10 【样例输出】
14 【样例说明】
如果我们用 0 代表遇到花， 1 代表遇到店， 14 种顺序如下：
- 010101101000000
- 010110010010000
- 011000110010000
- 100010110010000
- 011001000110000
- 100011000110000
- 100100010110000
- 010110100000100
- 011001001000100
- 100011001000100
- 100100011000100
- 011010000010100
- 100100100010100
- 101000001010100
【评测用例规模与约定】
对于 40 % 的评测用例： 1 ≤ N , M ≤ 10 。
对于 100 % 的评测用例： 1 ≤ N , M ≤ 100 。
算法标签：DP
f(i, j, k)表示一共遇到i个店， j朵花， 且有k个单位酒的方案的集合
集合按最后一步遇到的是花还是店来划分
所有酒的数量必须小于等于m
最后为店：f(i - 1, j, k / 2) , i >= 1 且 k / 2为整数
最后为花：f(i, j - 1, k + 1)， j >= 1
倒数第二步为：f(n, m - 1, 1)
代码：
#include
#include
using namespace std;
const int N = 105, mod = 1e9 + 7;
int f[N][N][N];
int main()
{
int n, m;
cin >> n >> m;
f[0][0][2] = 1;
for(int i = 0; i <= n; i++)
for(int j = 0; j <= m; j++)
for(int k = 0; k <= m; k++)
{
if(i >= 1 && k % 2 == 0)
f[i][j][k] = (f[i][j][k] + f[i - 1][j][k / 2]) % mod;
if(j >= 1)
f[i][j][k] = (f[i][j][k] + f[i][j - 1][k + 1]) % mod;
}
cout << f[n][m - 1][1] << endl;
return 0;
} J: 砍竹子
时间限制 : 1.0s
内存限制 : 256.0MB
本题总分： 25 分
【问题描述】
这天，小明在砍竹子，他面前有 n 棵竹子排成一排，一开始第 i 棵竹子的
高度为 h i .
他觉得一棵一棵砍太慢了，决定使用魔法来砍竹子。魔法可以对连续的一
段相同高度的竹子使用，假设这一段竹子的高度为 H ，那么使用一次魔法可以 把这一段竹子的高度都变为
，其中 
表示对 x 向下取整。小明想知道他最少 使用多少次魔法可以让所有的竹子的高度都变为1。
，其中 表示对 x 向下取整。小明想知道他最少 使用多少次魔法可以让所有的竹子的高度都变为1。
【输入格式】
第一行为一个正整数 n ，表示竹子的棵数。
第二行共 n 个空格分开的正整数 h i ，表示每棵竹子的高度。
【输出格式】
一个整数表示答案。
【样例输入】
6
2 1 4 2 6 7 【样例输出】
5 【样例说明】
其中一种方案：
2 1 4 2 6 7
→ 2 1 4 2 6 2
→ 2 1 4 2 2 2
→ 2 1 1 2 2 2
→ 1 1 1 2 2 2
→ 1 1 1 1 1 1
共需要 5 步完成
【评测用例规模与约定】
对于 20 % 的数据，保证 n ≤ 1000 , h i ≤ 。
。
对于 100 % 的数据，保证 n ≤ 2 × 
, h i ≤ 。
, h i ≤ 。
算法标签：贪心
#include
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 200010, M = 10;
int n, m;
LL f[N][M];
int main()
{
scanf("%d", &n);
LL stk[M];
int res = 0;
for(int i = 0; i < n; i++)
{
LL x;
int top = 0;
scanf("%lld", &x);
while(x > 1) stk[++top] = x, x = sqrt(x / 2 + 1);
res += top; //top为操作次数
m = max(m, top); //m表示所有数中的最大的操作次数
for(int j = 0, k = top; k; j++, k--)
f[i][j] = stk[k];
}
for(int i = 0; i < m; i++)
for(int j = 1; j < n; j++)
if(f[j][i] && f[j][i] == f[j - 1][i]) //当该数与前一个数相等时
res--;
cout << res << endl;
return 0;
}