【大数据】美国新冠肺炎疫情分析——错误版（QDU）

这个版本有些错误，整体思路上的错误，正确的版本中会直接使用该错误版本中的一些细节思路，所以还是建议先理解该错误版本，再看正确版本（其实是当时老师觉得我们做的太拉了，所以让我们重做，我才有机会重新思考，比较高质量的完成）

• 【大数据】蔬菜价格分析（QDU）
• 【大数据】美国新冠肺炎疫情分析——错误版（QDU）
• 【大数据】美国新冠肺炎疫情分析——正确版（QDU）
• 【大数据】乳腺癌预测——老师给的链接（QDU）
• 由于kaggle上“猫狗大战”的测试集标签是错的，所以没做出来，用的github上的代码
• 【大数据】《红楼梦》作者分析（QDU）

问题分析

已知从2020年1月28日到2020年9月8日新冠肺炎患者“新增”数量、“总确诊”数量、“总治愈”数量和“总死亡”数量，分析这若干个月内数量变化规律并构建合适的模型预测未来一个月数量的变化趋势。

解决思路

思考过程分为了三个递进的阶段：多项式拟合独立预测；分析数量变化率而非数量；关联四种已知信息构建最终模型

多项式拟合独立分析

最初没有考虑到四种信息之间的关系，只单独地对每种信息进行了多项式拟合预测趋势，这样的思考的好处在于模型简单且独立，缺点是与实际情况偏差太大，甚至存在与实际情况不符的情况。

分析数量变化率而非数量变化

针对“治愈率”和”死亡率“进行预测具有一定的合理性：

1. ”治愈数量“和”死亡数量“的变化完全可以由”治愈率“和”死亡率“反映出来。
2. 变化率与样本总数有关，相较于”数量变化“能更好的显示出”治愈数量“和”死亡数量“在”现存确诊“中的比例，反映现实情况更佳。
3. 对变化率的分析更符合实际情况。

关联四种已知信息并构建最终模型

对四种信息进行独立预测是没意义的，因此模型要建立在“新增”数量、“总确诊”数量、“总治愈”数量和“总死亡”数量相互关联的基础上。

在关联四种信息之前，我们需要先了解四者之间的关系。

先定义如下若干变量：

1. $治{愈}_n$：表示第n天的治愈总数，$治{愈}_n=治愈{率}_n\times 现存确{诊}_{n-1}+治{愈}_{n-1}$
2. $死{亡}_n$：表示第n天的死亡总数，$死{亡}_n=死亡{率}_n\times 现存确{诊}_{n-1}+死{亡}_{n-1}$
3. $现存确{诊}_n$：表示第n天现存的确诊人数，$现存确{诊}_n=总确{诊}_n-治{愈}_n-死{亡}_n$
4. $治愈{率}_n$：表示第n天的治愈率，$治愈{率}_n=(治{愈}_n-治{愈}_{n-1})/现存确{诊}_{n-1}$
5. $死亡{率}_n$：表示第n天的死亡率，$死亡{率}_n=(死{亡}_n-死{亡}_{n-1})/现存确{诊}_{n-1}$
6. $新{增}_n$：表示第n天的新增确诊数量，预测的数据
7. $总确{诊}_n$：表示第n天的确诊总数，$总确{诊}_n=总确{诊}_{n-1}+新{增}_n$

日期\类型	新增	总确诊	治愈	死亡
...	...	...	...	...
n-1	新增n-1	总确诊n-1	治愈n-1	死亡n-1
n	新增n	总确诊n	治愈n	死亡n

假设我们通过某种方式拟合出了”新增数量“曲线，即未来一个月的”新增“均可以确定，根据公式 $总确{诊}_n=总确{诊}_{n-1}+新{增}_n$ 通过迭代可以算出未来一个月的”总确诊“。

假设第n-1天的四种信息全部已知，则根据公式 $现存确{诊}_{n-1}=总确{诊}_{n-1}-治{愈}_{n-1}-死{亡}_{n-1}$ 可以算出第n-1天的现存确诊人数；我们通过某种方式对”治愈率“和“死亡率”进行预测，即得到未来一个月的”治愈率“和“死亡率”；通过公式 $X的变化{率}_n=(X_n-X_{n-1})/现存确{诊}_{n-1}$ 迭代算出未来一个月每天的“治愈率”和“死亡率”。

解决方案

第一阶段：多项式拟合独立预测

这是最初的建模思路，对每种信息进行独立的多项式拟合获取未来一个月的信息。

多项式拟合的实现

对给定数据$(x_i,y_i)(i=0,1,...,m)$，一共$m+1$个数据点，取多项式$P(x)$，使
$$\sum _{i=0}^m{r}_i^2=\sum _{i=0}^m[P(x_i)-y_i{]}^2=min$$
函数$P(x)$称为拟合函数或最小二乘解，设$n$次多项式$P_n(x)={\sum }_{k=0}^n{a}_k{x}^k$，使得
$$I=\sum _{i=0}^m[P_n(x_i)-y_i{]}^2=\sum _{i=0}^m(\sum _{k=0}^n{a}_k{x}_i^k-y_i{)}^2=min$$
其中，$a_0$，$a_1$，$a_2$，…，$a_n$为待求未知数，即多项式每一项的系数，$n$为多项式的最高次幂，由此，该问题化为求
$$I=I(a_0,a_1,...,a_n)$$
的极值问题。由多元函数求极值的必要条件：
$$\frac{\partial I}{\partial a_j}=2\sum _{i=0}^m(\sum _{k=0}^n{a}_k{x}_i^k-y_i)x_i^{j}j=0,1,...,n$$
变形后得到：
$$\sum _{k=0}^n(\sum _{i=0}^m{x}_i^{j+k})a_k=\sum _{i=0}^m{x}_i^j{y}_{i}j=0,1,...,n$$
这是一个关于$a_0$，$a_1$，$a_2$，…，$a_n$的线性方程组，用矩阵表示如下：
$$\left[\begin{array}{cccc}m+1& {\sum }_{i=0}^m{x}_i& ...& {\sum }_{i=0}^m{x}_i^n\\ {\sum }_{i=0}^m{x}_i& {\sum }_{i=0}^m{x}_i^2& ...& {\sum }_{i=0}^m{x}_i^{n+1}\\ ⋮& ⋮& & ⋮\\ {\sum }_{i=0}^m{x}_i^n& {\sum }_{i=0}^m{x}_i^{n+1}& ...& {\sum }_{i=0}^m{x}_i^{2n}\end{array}\right]\left[\begin{array}{c}{a}_0\\ a_1\\ ⋮\\ a_n\end{array}\right]=\left[\begin{array}{c}{\sum }_{i=0}^m{y}_i\\ {\sum }_{i=0}^m{x}_i{y}_i\\ ⋮\\ {\sum }_{i=0}^m{x}_i^m{y}_i\end{array}\right]$$

因此，只要给出数据点$(x_i,y_i)$及个数$m$，再给出所要拟合的参数$n$，则即可求出未知数矩阵$(a_0,a_1,...,a_n)$

新增数量的预测曲线

方法一：采用六次多项式进行拟合

未来一个月的预测相对合理，但对过远的未来进行预测会出现数量爆炸的情况，预测效果不佳。（对于小于0的点默认为0）

方法二：采用一次多项式拟合（线性回归）

由左侧的子图可知训练的效果不佳，预测后续变化相对平稳，只能预测变化的大概趋势。

总确诊数量的预测曲线

方法一：采用三次多项式拟合

训练集的样本变化平稳，因此预测结果也比较合理。

方法二：采用逻辑斯蒂回归

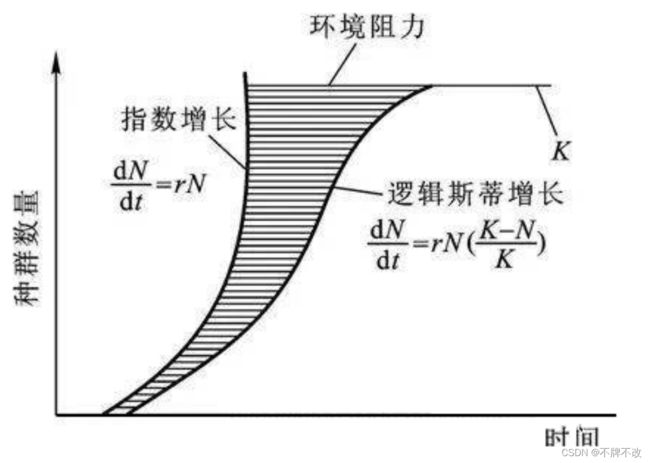
在理想状态下病毒的传播是不受限制的，呈指数形式增长。但实际的增长过程中增长速率并不能一直维持不变，因为病毒传播的过程中会受到一定的阻力，呈S型趋势增长。

当一个物种迁入到一个新生态系统中后，其数量会发生变化。假设该物种的起始数量小于环境的最大容纳量，则数量会增长。该物种在此生态系统中有天敌、食物、空间等资源也不足（非理想环境），则增长函数满足逻辑斯谛方程，图像呈S形，此方程是描述在资源有限的条件下种群增长规律的一个最佳数学模型。逻辑斯蒂模型的微分式是：$\frac{dx}{dt}=rx(1-x)$ 式中的r为速率参数。
$$P(t)=\frac{K{P}_0{e}^{rt}}{K+P_0(e^{rt}-1)}$$

• $K$为环境容量，即增长到最后，$P(t)$能达到的极限。
• $P_0$为初始容量，就是$t=0$时刻的数量。
• $r$为增长速率，$r$越大则增长越快，越快逼近$K$值，$r$越小增长越慢，越慢逼近$K$值。

---

logistic增长的曲线也称为s型曲线。下图左图为曲线数量，右图为增长速率。

---

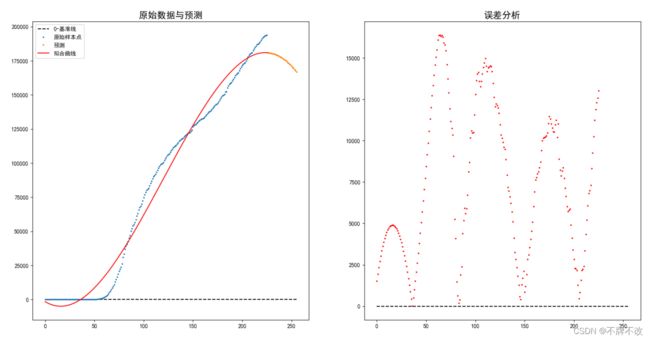
使用逻辑斯蒂模型对总确诊数量进行预测图如下：

（对于样本点先进行了步长为5的离散化，因为过度精确反而不利于非线性拟合参数的获取，因此通过离散化得到稀疏的样本点后再进行拟合）

总治愈数量的预测曲线

方法一：采用三次多项式拟合

训练集的样本变化平稳，因此预测结果也比较合理。

总死亡数量的预测曲线

方法一：采用三次多项式拟合

训练集存在波动导致对未来一个月的预测骤减，预测结果较差。

第二阶段：指数函数拟合变化率

总治愈数量的预测曲线

方法二：采用指数函数预测“治愈率”

设指数函数为$F(x)=a\cdot e^{-bx}+c$，其中$a$、$b$和$c$为参数，通过非线性拟合得到。

总死亡数量的预测曲线

方法二：采用指数函数预测“死亡率”

现实中，“治愈率”与“死亡率”应均为指数变化，随着技术的不断发展“治愈率”会越来越高，“死亡率”会越来越低。

第三阶段：关联四种已知信息并构建最终模型

对“新增”、“治愈率”和“死亡率”进行预测后，迭代得到未来一个月每天的“现存确诊数量”、“总确诊数量”、“总治愈数量”和“总死亡数量”。

最终预测曲线如下：

结果分析

整体模型预测效果比较合理，但严重依赖于对“新增数量”的预测。由于我采用了六次多项式拟合对“新增数量”进行预测，虽然未来一个月的预测相对合理，但由于存在爆炸现象，因此后续预测效果差。“新增数量”的模型的合理性对其他信息预测的准确性起到了决定性作用。

对未来100天的“新增数量”进行六次多项式拟合预测：

从图中可以看出预测100天已经呈爆炸式增长，与现实严重不符。

总结展望

优势

1. 对变化率进行训练和预测
2. 通过四种信息之间的关系将其关联
3. 通过迭代的方式使模型的合理性进一步提高

局限性

1. 未考虑环境等因素对数量的影响
2. “新增数量”的预测具有一定的不合理性

展望

1. 可以将季节、节假日等因素加入模型中进行预测
2. 使用更优质、更合适的模型对“新增数量”进行预测

附录（代码）

CoronaVirusPredict.py

用于调用子函数进行拟合，得到预测的数据后进行迭代并绘制图线。

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from xlrd import open_workbook
from NPolynomialFit import NPolynomialFit, calculate
from getFigure import getFigure
from getcolumn import getcolumn
from logistic import logistic_predict

def ExponentialFunction(x, a, b, c):
    return a * np.exp(-b * x) + c

original_data = open_workbook(r'C:\Users\23343\Desktop\test.xlsx')  # 打开文件
table = original_data.sheets()[0]

alldates = getcolumn(table, 0) # 获取第一列的日期
col1 = getcolumn(table, 1)
col2 = getcolumn(table, 2)
col3 = getcolumn(table, 3)
col4 = getcolumn(table, 4)

xi = range(len(alldates))

# ------------ 新增 ------------
# ----- 方法一 -----
increase, eachdayinc = getFigure(6, xi, col1, 0, len(alldates)) # k为六次多项式的系数 # 预测后续变化会数量爆炸，即预测效果不佳
# ----- 方法二 -----
# getFigure(1, xi, col1, 0, len(alldates)) # k为一次多项式的系数 # 训练效果不佳，预测后续变化相对平稳，即预测效果还可以

# ------------ 总确诊 ------------
# ----- 方法一 -----
# getFigure(3, xi, col2, 0, len(alldates)) # k为三次多项式的系数 # 预测后续变化相对合理，即预测效果还可以
# ----- 方法二 -----
# xi = [int(xi[i]/5) for i in range(0, len(xi), 5)] # 取点离散化，过于精确反而不利于模型训练与预测
# col2 = [col2[i] for i in range(0, len(col2), 5)]
# logistic_predict(xi, col2) # 逻辑斯蒂回归
# ----- 方法三 -----
# 对“新增”使用六次多项式拟合后，根据新增计算总确诊
# 这种方法的好处在于将“新增”与“总确诊”的关系加入模型中
# plt.figure(2)
# plt.plot(xi, col2, 's', markersize='2')  # 原始样本点
# plt.plot(range(len(xi), len(xi)+30), np.array(col2[len(col2)-1]) + increase, 'sr', markersize='2') # 预测未来一个月的总确诊
# plt.legend(["原始样本点", "预测"])
# plt.title("原始数据与预测", fontsize = '16')
# plt.show()
predict_allpatients = np.array(col2[len(col2)-1]) + increase

# ------------ 计算现存患者数 ------------
alive = np.array(col2) - np.array(col3) - np.array(col4)

# ------------ 总治愈 ------------
# ----- 方法一 -----
# getFigure(3, xi, col3, 0, len(alldates)) # k为三次多项式的系数 # 预测后续变化相对合理，即预测效果还可以
# ----- 方法二 -----
# 指数函数拟合，考虑到了实际情况，死亡率同
# 重点看治愈率，对治愈率进行预测
# plt.figure(2)
rate_recovery = [(col3[i + 1] - col3[i]) / alive[i] for i in range(len(col3)-1)]
rate_recovery = np.array(rate_recovery) # 治愈率 = (当日治愈总数 - 前日治愈总数)/前日现存确诊人数
idx_notzero = np.where((rate_recovery != 0) & (rate_recovery < 0.075))[0] # 去掉前面误差较大的点（最开始治愈率低是因为未找到治愈方式）
idx_notzero = [idx_notzero[i] for i in range(0, len(idx_notzero))]
rate_recovery_discretization = [rate_recovery[i] for i in idx_notzero]
# plt.plot(range(1, len(xi)), rate_recovery, 'sr', markersize = '2')
popt, pcov = curve_fit(ExponentialFunction, idx_notzero, rate_recovery_discretization, bounds=([0, -1, 0], [np.inf, 0, 50])) # 指数函数拟合
# plt.plot(range(1, len(xi)+30), ExponentialFunction(range(1, len(xi)+30), popt[0], popt[1], popt[2]), '--')
# plt.plot(range(len(xi), len(xi)+30), ExponentialFunction(range(len(xi), len(xi)+30), popt[0], popt[1], popt[2]), 'sb', markersize = '2')
predict_recovery_rate = ExponentialFunction(range(len(xi), len(xi)+30), popt[0], popt[1], popt[2]) # 预测未来一个月的治愈率
# plt.legend(["样本点","拟合曲线","预测"])
# plt.title("治愈总数的曲线变化预测")
# plt.show()

# ------------ 总死亡 ------------
# ----- 方法一 -----
# getFigure(3, xi, col4, 0, len(alldates)) # k为三次多项式的系数 # 预测后续变化骤降，即效果不佳
# ----- 方法二 -----
# 重点看死亡率，对死亡率进行预测
rate_death = [(col4[i + 1] - col4[i]) / alive[i] for i in range(len(col4) - 1)]
rate_death = np.array(rate_death) # 治愈率 = (当日治愈总数 - 前日治愈总数)/前日现存确诊人数
idx_notzero = np.where((rate_death != 0))[0] # 去掉前面误差较大的点
idx_notzero = [idx_notzero[i] for i in range(0, len(idx_notzero))]
rate_death_discretization = [rate_death[i] for i in idx_notzero]
# plt.plot(range(1, len(xi)), rate_death, 'sr', markersize ='2')
popt, pcov = curve_fit(ExponentialFunction, idx_notzero, rate_death_discretization, bounds=([0, 0, 0], [np.inf, 1, 10])) # 指数函数拟合
# plt.plot(range(1, len(xi)+30), ExponentialFunction(range(1, len(xi)+30), popt[0], popt[1], popt[2]), '--')
# plt.plot(range(len(xi), len(xi)+30), ExponentialFunction(range(len(xi), len(xi)+30), popt[0], popt[1], popt[2]), 'sb', markersize = '2')
predict_death_rate = ExponentialFunction(range(len(xi), len(xi)+30), popt[0], popt[1], popt[2]) # 预测未来一个月的死亡率
# plt.legend(["样本点","拟合曲线","预测"])
# plt.title("死亡总数的曲线变化预测")
# plt.show()

# ------------ 用以下四个信息进行迭代 ------------
predict_allpatients = np.array(predict_allpatients)
predict_recovery_rate = np.array(predict_recovery_rate)
predict_death_rate = np.array(predict_death_rate)
alive = [alive[len(alive)-1]]                             # 第n-1年现存患者数（仅方便自己理解）
recovery = [col3[len(col3)-1]]                            # 第n-1年的治愈总数（仅方便自己理解）
death = [col4[len(col4)-1]]                               # 第n-1年的死亡总数（仅方便自己理解）

predict_days = 30
for days in range(predict_days):
     recovery.append(predict_recovery_rate[days] * alive[days] + recovery[days])
     death.append(predict_death_rate[days] * alive[days] + death[days])
     alive.append(predict_allpatients[days] - recovery[days+1] - death[days+1])

# ------------ 绘制 ------------
plt.subplot(221)
plt.plot(range(0, len(xi)), col1, 'sr', markersize ='2')
plt.plot(range(len(xi), len(xi)+predict_days), eachdayinc, 'sb', markersize='2')
plt.legend(["样本点", "预测点"])
plt.title("新增数量的曲线变化预测", fontsize = "16")

plt.subplot(222)
plt.plot(range(0, len(xi)), col2, 'sr', markersize ='2')
plt.plot(range(len(xi), len(xi)+predict_days), predict_allpatients, 'sb', markersize='2')
plt.legend(["样本点", "预测点"])
plt.title("确诊总数的曲线变化预测", fontsize = "16")

plt.subplot(223)
plt.plot(range(0, len(xi)), col3, 'sr', markersize ='2')
plt.plot(range(len(xi), len(xi)+predict_days), recovery[1:], 'sb', markersize='2')
plt.legend(["样本点", "预测点"])
plt.title("治愈总数的曲线变化预测", fontsize = "16")

plt.subplot(224)
plt.plot(range(0, len(xi)), col4, 'sr', markersize ='2')
plt.plot(range(len(xi), len(xi)+predict_days), death[1:], 'sb', markersize='2')
plt.legend(["样本点", "预测点"])
plt.title("死亡总数的曲线变化预测", fontsize = "16")

plt.show()

getFigure.py

调用多项式拟合函数并获取预测值进行绘图。

import numpy as np
import matplotlib.pyplot as plt
from NPolynomialFit import NPolynomialFit, calculate


def getFigure(n, xi, yi, l, r, days = 30):
    k, x, y, xi_y = NPolynomialFit(n, xi, yi, l, r)  # n为多项式拟合次数，xi、yi为样本点，l、r表示预测区间
    error = abs(np.array(xi_y) - np.array(yi)) # 计算误差

    sub1 = plt.subplot(121)
    plt.plot(range(len(xi)+days), np.zeros(len(xi)+days), '--k')  # 基准线
    plt.plot(xi, yi, 's', markersize='2')  # 原始样本点
    predict_days = range(len(xi), len(xi)+days)
    predict_nums = calculate(k, predict_days)
    plt.plot(predict_days, predict_nums, 's', markersize='2')
    plt.plot(x, y, '-r')  # 拟合曲线
    sub1.set_title("原始数据与预测", fontsize = '16')
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    plt.legend(["0-基准线", "原始样本点", "预测", "拟合曲线"])

    sub2 = plt.subplot(122)
    plt.plot(range(len(xi)+days), np.zeros(len(xi)+days), '--k')  # 基准线
    plt.plot(xi, error, 'sr', markersize='2')
    sub2.set_title("误差分析", fontsize = '16')

    plt.show()

    return np.array(predict_nums).cumsum(), predict_nums

NPolynomialFit.py

实现n次多项式拟合。

import math
import numpy as np
from numpy.linalg import inv

def calculate(k, x):
    y = []
    for xi in x:
        mi = 0
        tmp = 0
        for ki in k:
            tmp = tmp + ki*math.pow(xi, mi)
            mi = mi + 1
        y.append(tmp)
    return y

def NPolynomialFit(n, xi, yi, l, r):
    """xi，yi表示样本数据集，l，r表示要拟合的区间"""

    m = len(xi)-1 # 总共m+1个样本点
    A = [[0 for j in range(n+1)] for i in range(n + 1)]
    B = [[0] for i in range(n+1)]

    for row in range(n + 1):
        for col in range(n + 1):
            for i in range(m + 1):
                A[row][col] = A[row][col] + math.pow(xi[i], row + col) # 多项式系数的“系数”

    for row in range(n + 1):
        for i in range(m + 1):
            B[row][0] = B[row][0] + yi[i] * math.pow(xi[i], row) # 得到等式右侧式子

    A = np.array(A)
    B = np.array(B)
    k = np.dot(inv(A), B) # 计算多项式的系数
    k = [i[0] for i in k.tolist()]  # 化二维为一维

    x = [l + i * 0.001 for i in range((r-l)*1000)] # 以0.001为步长从l取到r
    y = calculate(k, x) # 计算对应的y值
    xi_y = calculate(k, xi)
    return k, x, y, xi_y

logistic.py

逻辑斯蒂模型预测并绘图。

import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt

def logistic_increase_function(t,K,P0,r):
    # t:time   t0:initial time    P0:initial_value    K:capacity  r:increase_rate
    t0 = 0
    exp_value=np.exp(r*(t-t0))
    return (K*exp_value*P0)/(K+(exp_value-1)*P0)

def logistic_predict(xi, yi):
    step=5

    xi = np.array(xi)
    yi = np.array(yi)

    # 调参
    popt, pcov = curve_fit(logistic_increase_function, xi, yi, bounds=([35000000, -np.inf, -np.inf], [np.inf, np.inf, np.inf]))
    xi_y = logistic_increase_function(xi, popt[0], popt[1], popt[2])

    tomorrow = [xi[xi.shape[0]-1] + i for i in range(1, 60)]
    tomorrow = np.array(tomorrow)
    tomorrow_predict = logistic_increase_function(tomorrow, popt[0], popt[1], popt[2])

    # 绘图
    plot1 = plt.plot(xi*step, yi, 's', label="confimed infected people number")
    plot2 = plt.plot(xi*step, xi_y, 'r', label='predict infected people number')
    plot3 = plt.plot(tomorrow*step, tomorrow_predict, 'b', label='predict infected people number')
    plt.xlabel('time')
    plt.ylabel('confimed infected people number')

    plt.legend(loc=0)  # 指定legend的位置右下角

    print(logistic_increase_function(np.array(28), popt[0], popt[1], popt[2]))
    print(logistic_increase_function(np.array(29), popt[0], popt[1], popt[2]))
    plt.show()

getcolumn.py

获取每列的数据信息。

from datetime import datetime

def getcolumn(table, i):
    res = []
    for val in table.col_values(i):
        if i == 0:
            if len(val) != 2:
                date = val.split('.')
                res.append(datetime(int(date[0]), int(date[1]), int(date[2])))
        else:
            try:
                res.append(int(val))
            except:
                continue
    return res