机器学习——正则化逻辑回归(分类)编程训练
机器学习——正则化逻辑回归(分类)编程训练
参考资料:
1.黄海广老师:吴恩达机器学习笔记github
本文是吴恩达机器学习课程中的第二个编程训练的第二部分。关于逻辑回归的详细介绍可以参考吴恩达机器学习课程
编程任务:
实现如下数据的分类问题:
0.过拟合介绍
当我们处理的数据较为复杂时,我们可以通过增添特征或者增加高次项来获得较好的拟合结果。
例如在线性回归中:
假设函数(1): h θ ( x ) = θ 0 x 0 + θ 1 x h_θ(x) = θ_0x_0 + θ_1x hθ(x)=θ0x0+θ1x
假设函数(2): h θ ( x ) = θ 0 x 0 + θ 1 x + θ 2 x 2 h_θ(x) = θ_0x_0 + θ_1x + θ_2x^2 hθ(x)=θ0x0+θ1x+θ2x2
假设函数(3): h θ ( x ) = θ 0 x 0 + θ 1 x + θ 2 x 2 + θ 3 x 3 h_θ(x) = θ_0x_0 + θ_1x + θ_2x^2+θ_3x^3 hθ(x)=θ0x0+θ1x+θ2x2+θ3x3
上述三种假设函数则对应三种情况,欠拟合,正常拟合,过拟合。
-
欠拟合:可以理解为得到一条描述数据趋势的大致直线
-
正常拟合:可以理解为得到一条更加精确描述数据趋势的曲线
-
过拟合:可以理解为得到一条曲线,数据的每个点都在这条曲线上
过拟合得到的假设函数,在训练集上表现很好,但是在验证集上并不能够很好的拟合
1.过拟合的解决办法
-
减少特征的数量
通常情况下,过拟合产生的原因就是特征的数量过多,例如上述的假设函数(3)的特征数量多达4个。
而在这些特征中,有些特征其实是没有必要的,其为拟合增添了过多的约束,导致拟合结果在其他新样本上无法正常工作。因此减少特征的数量,是假设函数从(3)到(2)即可解决过拟合问题
-
正则化
正则化的意义与上述减少特征的数量在本质上是一致的,不过,正则化并不直接操作特征,而是操作特征所对应的系数,即 θ θ θ。
例如假设函数(3),我们在不改变特征的情况下,想要将其变为(2),则需要使 θ 3 θ_3 θ3趋向于0
2.正则化
以线性回归为例讲解正则化原理,例如下述假设函数导致数据过拟合:
h θ ( x ) = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 2 + θ 3 x 3 3 + θ 4 x 4 4 h_θ(x) = θ_0x_0 + θ_1x_1+θ_2x_2^2+θ_3x_3^3+θ_4x_4^4 hθ(x)=θ0x0+θ1x1+θ2x22+θ3x33+θ4x44
采用正则化,则是使得 θ 3 , θ 4 θ_3,θ_4 θ3,θ4趋向于0。
其代价函数为:
J ( θ ) = 1 2 m ∑ m [ h θ ( x ( i ) − y ( i ) ] 2 J(θ) = \frac{1}{2m}\sum^m[h_θ(x^{(i)}-y^{(i)}]^2 J(θ)=2m1∑m[hθ(x(i)−y(i)]2
我们修改其代价函数为:
J ( θ ) = 1 2 m [ ∑ m [ h θ ( x ( i ) − y ( i ) ] 2 + 1000 θ 3 2 + 1000 θ 4 2 ] J(θ) = \frac{1}{2m}[\sum^m[h_θ(x^{(i)}-y^{(i)}]^2+1000θ_3^2+1000θ_4^2] J(θ)=2m1[∑m[hθ(x(i)−y(i)]2+1000θ32+1000θ42]
由于我们要最小化代价函数,因此通过不断迭代,如梯度下降法、牛顿法等等,最终得出的结果, θ 3 , θ 4 θ_3,θ_4 θ3,θ4是趋向于0的。我们称该过程为正则化。
但是通常情况下我们并不知道哪一项特征需要正则化,因此,我们选择将所有特征的都进行正则化,则代价函数修改为:
J ( θ ) = 1 2 m [ ∑ m [ h θ ( x ( i ) − y ( i ) ] 2 + λ ∑ j = 1 n θ j 2 ] J(θ) = \frac{1}{2m}[\sum^m[h_θ(x^{(i)}-y^{(i)}]^2+λ\sum^n_{j=1}θ_j^2] J(θ)=2m1[∑m[hθ(x(i)−y(i)]2+λj=1∑nθj2]
通常情况下我们对 θ 0 θ_0 θ0并不进行正则化,因此, j j j的取值从1开始, n n n代表一个样本中特征的数量。
在逻辑回归中,代价函数修正为:
J ( θ ) = 1 m ∑ m [ − y ( i ) log ( h θ ( x ( i ) ) − ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(θ) = \frac{1}{m}\sum^m[-y^{(i)}\log(h_θ(x^{(i)})-(1-y^{(i)})\log(1-h_θ(x^{(i)})]+\frac{λ}{2m}\sum^n_{j=1}θ_j^2 J(θ)=m1∑m[−y(i)log(hθ(x(i))−(1−y(i))log(1−hθ(x(i))]+2mλj=1∑nθj2
3.梯度下降法
通过观察可以知道,未进行正则化之前,线性回归和逻辑回归,二者的偏导,在形式上是一样的,因此增加了正则项后,二者的偏导在形式上仍是一样的。
偏导:
∂ J ( θ ) ∂ θ = 1 m ∑ m ( h θ ( x ( i ) ) − y ( i ) ) x ( i ) + λ m θ j \frac{∂J(θ)}{∂θ} =\frac{1}{m}\sum^m(h_θ(x^{(i)}) -y^{(i)})x^{(i)} + \frac{λ}{m}θ_j ∂θ∂J(θ)=m1∑m(hθ(x(i))−y(i))x(i)+mλθj
通过比较线性回归和逻辑回归的梯度下降法,不难发现,关于 θ θ θ的更新是一致的,因此在正则化后的梯度下降法中,二者也是一致的。
θ θ θ的更新迭代:
θ 0 = θ 0 − α 1 m ∑ m [ h θ ( x ( i ) − y ( i ) ] x 0 ( i ) θ j = θ j − α [ 1 m ∑ m [ h θ ( x ( i ) − y ( i ) ] x j ( i ) + λ m θ j ] = θ j ( 1 − α λ m ) − α m ∑ m [ h θ ( x ( i ) − y ( i ) ] x j ( i ) θ_0 = θ_0-α\frac{1}{m}\sum^m[h_θ(x^{(i)}-y^{(i)}]x_0^{(i)}\\ θ_j = θ_j-α[\frac{1}{m}\sum^m[h_θ(x^{(i)}-y^{(i)}]x_j^{(i)}+\frac{λ}{m}θ_j]\\ =θ_j(1-\frac{αλ}{m})-\frac{α}{m}\sum^m[h_θ(x^{(i)}-y^{(i)}]x_j^{(i)} θ0=θ0−αm1∑m[hθ(x(i)−y(i)]x0(i)θj=θj−α[m1∑m[hθ(x(i)−y(i)]xj(i)+mλθj]=θj(1−mαλ)−mα∑m[hθ(x(i)−y(i)]xj(i)
关于梯度下降法在本例中仅做介绍,并不使用。本例使用的最小化优化算法是“TNC”法,又称为截断牛顿法。
4.正则化逻辑回归(分类)流程
- 读取数据
- 获取特征值
- 获取标签值
- 特征缩放
- 特征映射
- 构建特征与标签之间的函数关系(假设函数)
- 构建正则化代价函数
- 求取正则化代价函数的偏导数
- 最小正则化化代价函数,并获取到此时的权重
- 根据权重得到特征与标签之间的函数关系
特征映射:通过已有的特征,构造出额外的特征,增加假设函数中的特征,来提升拟合效果,之后为了防止过拟合,需要进行正则化。
构建正则化代价函数,与之前的构建代价函数是相似的,仅仅增加了正则项。
5. 决策边界
如开篇的图片所示,想要通过 X × θ = 0 X × θ=0 X×θ=0的等式,来推导出决策边界的方程是很复杂的。
因此,我们通过找到所有满足 X × θ = 0 X × θ=0 X×θ=0的特征,并将特征所对应的点画出来,就可以得到决策边界
- 将特征1,特征2所组成的特征平面(即开篇的图片)进行网格划分
- 获取到网格上的交叉点
- 将交叉点进行特征映射,获取新的特征 X X X
- 代入 X × θ X × θ X×θ中进行计算,获取到满足 X × θ = 0 X × θ=0 X×θ=0的特征
- 获得满足条件的特征所对应的交叉点,该交叉点就是决策边界上的点
6.代码实现
数据集:来自黄海广老师的GitHub仓库,具体链接
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import scipy.optimize as opt
from sklearn.metrics import classification_report # 这个包是评价报告
def get_X(df): # 获取特征
ones = pd.DataFrame({'ones': np.ones(len(df))})
data = pd.concat([ones, df], axis=1)
return data.iloc[:, :-1].values
def get_y(df): # 获取标签
return np.array(df.iloc[:, -1])
def normalize_feature(df): # 特征缩放
return df.apply(lambda column: (column - column.mean()) / column.std())
def feature_mapping(x, y, power, as_ndarray=False):
'''
特征映射函数,来创建更多的特征,提升拟合效果
:param x: 特征1
:param y: 特征2
:param power: 创建特征的最高次
:param as_ndarray: 创建的数据是否为ndarray数据类型
:return:
f00 f10 f01 f20 f11 f02 f30 f21 f12 f03
x^0y^0 x^1y^0 x^0y^1 x^2y^0 x^1y^1 x^0y^2 x^3y^0 x^2y^1 x^1y^2 x^0y^3……
'''
data = {"f{}{}".format(i - p, p): np.power(x, i - p) * np.power(y, p)
for i in np.arange(power + 1)
for p in np.arange(i + 1)
}
if as_ndarray:
return pd.DataFrame(data).values
else:
return pd.DataFrame(data)
def sigmoid(z): # 定义sigmoid函数
return 1 / (1 + np.exp(-z))
def cost(theta, X, y): # 定义代价函数,这里需要注意X,theta,y的维度
return np.mean(-y * np.log(sigmoid(X @ theta)) - (1 - y) * np.log(1 - sigmoid(X @ theta)))
# (100,1)*[(100,3)(3,1)] 这里并不影响计算计算结果
# 值得一提的是,在numpy中,+,-,*,/都只是相对应元素的运算,不遵循矩阵计算规则
# numpy中的矩阵计算需要使用@或者.dot()函数
# 同样也可以将ndarray类型数据通过np.matrix()转换成矩阵,使用*进行计算
def regularized_cost(theta, X, y, l=1): # 正则化代价函数 l 为正则系数
'''
代价函数正则项:λ/2m * sum(θ_j^2) j 从 1 到 n
:param theta: 权重系数
:param X: 特征
:param y: 标签
:param l: 正则系数 λ
:return: 带有正则项的代价函数
'''
theta_j1_to_n = theta[1:] # 从θ_1到θ_n ,通常情况下,我们不对θ_0进行正则化
regularized_term = (l / (2 * len(X))) * np.power(theta_j1_to_n, 2).sum() # 代价函数正则项,是一个数值
return cost(theta, X, y) + regularized_term
def gradient(theta, X, y): # 求偏导
return (1 / len(X)) * X.T @ (sigmoid(X @ theta) - y) # (3,100)[(100,3)(3,1)]====>(3,1)
def regularized_gradient(theta, X, y, l=1): # 正则化偏导 l 为正则系数
'''
代价函数偏导正则项:λ/m * θ_j
:param theta: 权重系数
:param X: 特征
:param y: 标签
:param l: 正则系数λ
:return: 带有正则项的代价函数偏导
'''
theta_j1_to_n = theta[1:] # # 从θ_1到θ_n
regularized_theta = (l / len(X)) * theta_j1_to_n # 代价函数偏导正则项,是一个数组
# 由于没有正则化θ_0,因此拼接一个数组0,保证数组维数
regularized_term = np.concatenate([np.array([0]), regularized_theta])
return gradient(theta, X, y) + regularized_term
def predict(x, theta): # 预测函数,用来进行验证
prob = sigmoid(x @ theta)
return (prob >= 0.5).astype(int)
def feature_mapped_logistic_regression(power, l): # 主函数部分
'''
如果不考虑决策边界的绘制,这里应当是主函数。
为了方便下文决策边界函数的调用,将该段定义为一个函数
:param power: 特征映射的最高次方
:param l: 正则系数 λ
:return: 通过数据拟合后的最终的权重系数 θ
'''
df = pd.read_csv('ex2data2.txt', names=['test1', 'test2', 'accepted'])
x1 = np.array(df.test1) # 读取特征1
x2 = np.array(df.test2) # 读取特征2
y = get_y(df) # 获取标签
X = feature_mapping(x1, x2, power, as_ndarray=True) # 对特征1,特征2进行特征映射,获得新的特征数据
theta = np.zeros(X.shape[1]) # 定义θ 要和特征数据维度相同
# 使用优化器中的优化函数,采用的方法是TNC“截断牛顿法”
res = opt.minimize(fun=regularized_cost,
x0=theta,
args=(X, y, l),
method='TNC',
jac=regularized_gradient)
final_theta = res.x # 获取最终的θ值
y_pred = predict(X, final_theta) # 对原有的数据特征进行预测
print(classification_report(y, y_pred)) # 真实值,预测值,进行比较,输出评价报告
return final_theta
def find_decision_boundary(density, power, theta, threshhold): # 寻找决策边界
'''
该函数用来寻找决策边界
已知决策边界的方程为 x*θ=0,我们已知 θ
因此,我们只需要找到可以令 x*θ=0 或者接近于0 的特征,我们就可以画出来决策边界
我们将特征1和特征2组成的特征平面划分成网格,将每个网格交叉点的对应的特征代入到方程中,判断其是否接近于0
:param density: 沿 x,y 平均划分的网格数量
:param power: 特征缩放的最高次
:param theta: 最终的权重系数
:param threshhold: 门限值(阈值)
:return: 满足门限值的点x,y坐标
'''
t1 = np.linspace(-1, 1.5, density) # 通过观察数据,我们发现特征1和特征2的数值都分布在(-1,1.5)之间
t2 = np.linspace(-1, 1.5, density) # 因此(-1,1.5)就是我们所需要的有效的特征平面,对其进行网格划分
cordinates = [(x, y) for x in t1 for y in t2] # 获取网格交叉点
x_cord, y_cord = zip(*cordinates) # 将表示交叉点的元组进行解压缩,获得所有的x坐标和y坐标,作为特征1和特征2
mapped_cord = feature_mapping(x_cord, y_cord, power) # 对特征1,特征2进行特征映射,获取新特征x
inner_product = mapped_cord.values @ theta # 计算x*θ
decision = mapped_cord[np.abs(inner_product) < threshhold] # 获取到x*θ接近于0的特征x
return decision.f10, decision.f01 # f10为特征1,f01为特征2
def draw_boundary(power, l): # 绘制决策边界
density = 1000 # 沿 x,y 平均划分的网格数量
threshhold = 2 * 10 ** -3 # 门限值
final_theta = feature_mapped_logistic_regression(power, l) # 最终的权重系数
x, y = find_decision_boundary(density, power, final_theta, threshhold) # 获取到的满足门限值的x,y即特征1,特征2
df = pd.read_csv('ex2data2.txt', names=['test1', 'test2', 'accepted']) # 读取数据,绘制散点图
sns.lmplot('test1', 'test2', hue='accepted', data=df, height=6, fit_reg=False, scatter_kws={"s": 100})
plt.scatter(x, y, c='r', s=10) # 绘制出满足门限值的点,即决策边界上的点
plt.title('Decision boundary (l = %d)' % l, loc="center", pad=0) # 定义标题
plt.show()
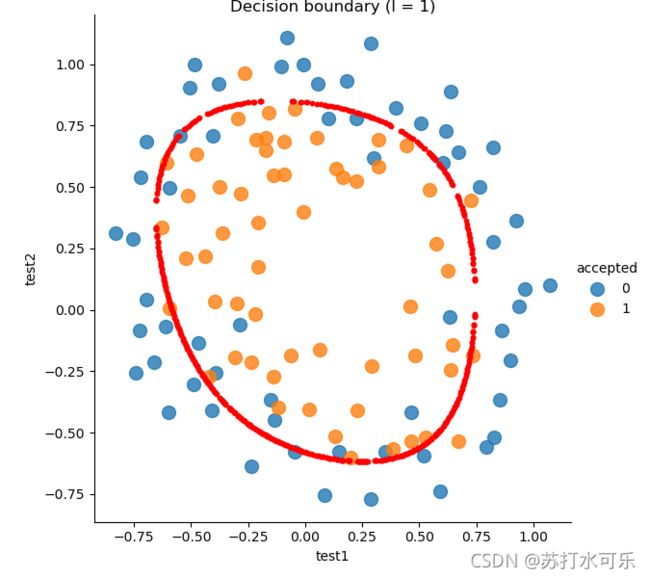
draw_boundary(power=6, l=1) # lambda=1
7.运行结果:
draw_boundary(power=6, l=1) # lambda=1 时
precision recall f1-score support
0 0.90 0.75 0.82 60
1 0.78 0.91 0.84 58
accuracy 0.83 118
macro avg 0.84 0.83 0.83 118
weighted avg 0.84 0.83 0.83 118
分类正确率达到83%,决策边界:
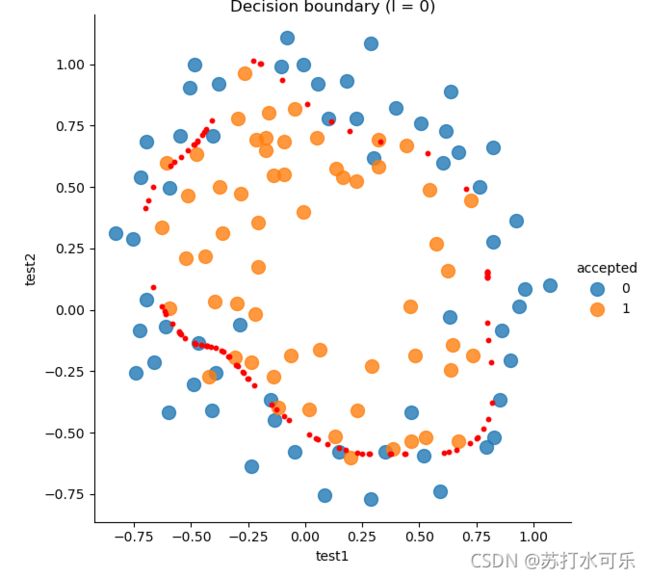
draw_boundary(power=6, l=0) # lambda=0 时,没有正则化,数据过拟合
precision recall f1-score support
0 0.91 0.83 0.87 60
1 0.84 0.91 0.88 58
accuracy 0.87 118
macro avg 0.88 0.87 0.87 118
weighted avg 0.88 0.87 0.87 118
分类正确率达到87%,决策边界:
draw_boundary(power=6, l=100) # lambda=100 时,欠拟合
precision recall f1-score support
0 0.59 0.75 0.66 60
1 0.64 0.47 0.54 58
accuracy 0.61 118
macro avg 0.62 0.61 0.60 118
weighted avg 0.62 0.61 0.60 118