目标检测与识别算法综述：从传统算法到深度学习(二)

作   者：XJTU_Ironboy
时   间：2018年11月
联系方式：[email protected]

本文结构：

1. 摘要
2. 介绍
   2.1 大致框架
   2.2 测试评价指标
   2.3 相关比赛介绍
   2.4 相关数据集介绍
3. 基于图像处理和机器学习算法
   3.1 滑动窗口
   3.2 提取特征
    3.1.1 Harr特征
    3.1.2 SIFT(尺度不变特征变换匹配算法)
    3.1.3 HOG(方向梯度直方图特征)
    3.1.4 SURF(加速稳健特征)
   3.3 分类器
   3.2 经典的检测算法
    3.2.1 Haar特征+Adaboost算法
    3.2.2 Hog特征+Svm算法
    3.2.3 DPM算法
4. 基于深度学习算法
   4.1 基于region proposal的目标检测与识别算法
    4.1.1 R-CNN
    4.1.2 SPP-Net
    4.1.3 Fast R-CNN
    4.1.4 Faster R-CNN
   4.2 基于regression的目标检测与识别算法
    4.2.1 YOLO
    4.2.2 SSD
    4.2.3 RFCN
    4.2.4 Mask-RCNN
   4.3 基于search的目标检测与识别算法
    4.3.1 基于视觉注意的AttentionNet
    4,3.2 基于强化学习的算法
5. 总结
6. 致未来

3. 基于图像处理和机器学习算法

  目标检测算法很早之前就已经出现了，由于它的实时性和精度不是很高，所以在深度学习火起来之前一直没能在工业界得到很好的应用，只是在类似于PASCAL VOC(2005-2012)这样的目标检测比赛中为大家所熟知。传统的目标检测方法是基于图像处理和机器学习算法的，主要的思路是：
  (1) 利用滑动窗口或选择性搜索等方法对一幅图像进行处理获取候选框；
  (2) 对每个框提取特征(Harr、HOG…), 判断是不是目标，若判定为目标则同时记录其位置坐标(x,y,w,h)–定位；
  (3) 利用分类器(Adaboost、决策树)对目标进行分类–识别。
  虽然分为了三步，但是在实际的检测中都是每获得一个候选框，立即提取其特征判断是不是目标，若是目标则用分类器判断为哪类；若不是，则继续提取下一个候选框。
  由于传统的目标检测方法相比于目前基于深度学习的算法在实时性和精度上都不能相提并论，所以从事计算机视觉的同学大概了解传统算法的核心思想就行，不需要过于追求其细节。下面的讲述将有所侧重，不会对每一个方法都讲的太详细。

3.1 获得候选框

  表示一幅图像中某目标的位置一般都是记录其左上角坐标(x,y)和他的宽度与高度(w,h)，即用一个矩形框将目标框起来表示检测到了该目标，这个矩形框又叫候选框，但不是每个候选框内都一定保证存在待检测的目标，实际操作中候选框的数目是远远大于最终目标数目的。
  那么候选框是如何产生，又是如何进行筛选的呢？其实物体候选框获取当前主要使用图像分割与区域生长技术。区域生长(合并)主要由于检测图像中存在的物体具有局部区域相似性(颜色、纹理等)。目标识别与图像分割技术的发展进一步推动有效提取图像中信息，下面主要讲两种常用的方法：滑动窗口和选择性搜索。
- 滑动窗口
  滑窗法作为一种经典的物体检测方法，我认为不同大小的窗口在图像上进行滑动时候，进行卷积运算得到其特征表示，然后用已经训练好的分类器判别该窗口中存在物体的概率。滑动窗口具体怎么操作：
step1: 设定目标可能存在的最小窗口的大小[w_min,h_min];
step2: 设定窗口从小到大的一个放大比例r和移动的步长step;
step3: 从图像的左上角(图像的原点)开始，划定一个最小的候选框，此时它的(x,y,w,h)信息是(0,0,w_min,h_min)；
step4: 对该候选框进行特征提取和分类；
step5: 窗口大小不变，位置按照从左到右，从上到下的顺序，每间隔步长step进行滑动一次，每滑动一次获得一个窗口，即跳转到step4进行检测，直到滑动到右下角不能再滑动为止；
step6: 接着继续从图像的左上角(图像的原点)开始，宽度和高度按上次滑动大小均扩大r倍，获得该大小下的第一个窗口，跳转到step4
step7: 直到最后一个窗口滑完，统计之前已经检测到的目标位置和类别，即完成对一副图像的目标检测；
- 选择性搜索
  选择性搜索(Selective Search)是主要运用图像分割技术来进行物体检测。滑窗法类似穷举进行图像子区域搜索，但是一般情况下图像中大部分子区域是没有物体的。学者们自然而然想到只对图像中最有可能包含物体的区域进行搜索以此来提高计算效率。选择搜索方法是当下最为熟知的图像候选框提取算法，由Koen E.A于2011年提出，具体详见论文(Selective Search for Object Recognition)。
下面大致说一下选择搜索算法获得候选框的过程：图像中物体可能存在的区域应该是有某些相似性或者连续性区域的。因此，选择搜索基于上面这一想法采用子区域合并的方法进行提取候选边界框。首先，对输入图像进行分割算法产生许多小的子区域。其次，根据这些子区域之间相似性(相似性标准主要有颜色、纹理、大小等等)进行区域合并，不断的进行区域迭代合并。每次迭代过程中对这些合并的子区域做一个大的外切矩形，这些子区域外切矩形就是通常所说的候选框。

  详细讲解可见文章(内含可实现代码)：目标检测之选择性搜索-Selective Search
  选择性搜索的优点：
　　(1) 计算效率优于滑窗法。
　　(2) 由于采用子区域合并策略，所以可以包含各种大小的疑似物体框。
　　(3) 合并区域相似的指标多样性，提高了检测物体的概率。

3.2 提取特征

3.1.1 Harr特征
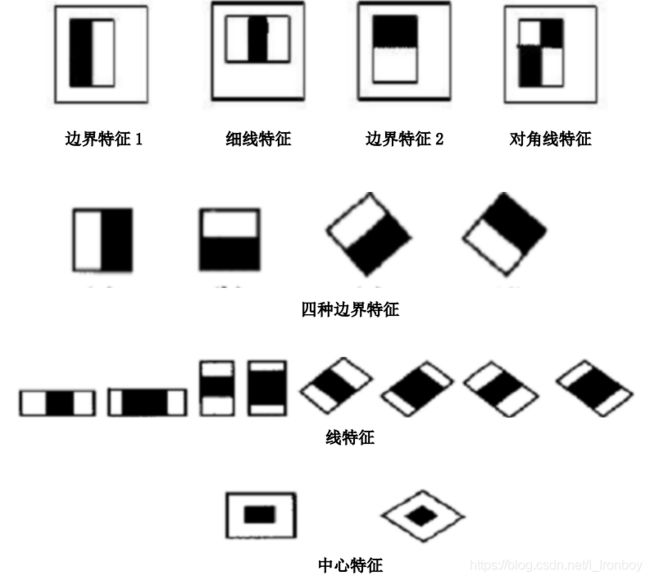
  Harr特征是一种反映图像的灰度变化的，像素分模块求差值的一种特征。它分为三类：边缘特征、线性特征、中心特征和对角线特征。以下是一些Harr特征的示例：

  用黑白两种矩形框组合成特征模板，在特征模板内用黑色矩形像素和减去白色矩形像素和来表示这个模版的特征值。例如：脸部的一些特征能由矩形模块差值特征简单的描述，如：眼睛要比脸颊颜色要深，鼻梁两侧比鼻梁颜色要深，嘴巴比周围颜色要深等。但矩形特征只对一些简单的图形结构，如边缘、线段较敏感，所以只能描述在特定方向（水平、垂直、对角）上有明显像素模块梯度变化的图像结构。
3.1.2 HOG(方向梯度直方图特征)
  方向梯度直方图（Histogram of Oriented Gradient, HOG）特征是一种在计算机视觉和图像处理中用来进行物体检测的特征描述子。HOG特征通过计算和统计图像局部区域的梯度方向直方图来构成特征。

• 通俗理解
    局部目标的外表和形状可以被局部梯度或边缘方向的分布很好的描述，即使我们不知道对应的梯度和边缘的位置。在实际操作中，将图像分为小的元胞(cells)，在每个元胞内累加计算出一维的梯度方向(或边缘方向)直方图。为了对光照和阴影有更好的不变性，需要对直方图进行对比度归一化，这可以通过将元胞组成更大的块(blocks)并归一化块内的所有元胞来实现。归一化的块描述符就叫作HOG描述子。将检测窗口中的所有块的HOG描述子组合起来就形成了最终的特征向量。
• HOG特征提取的基本步骤
  (1) 将彩色图像灰度化——[0,255]；
  (2) 采用Gamma校正法对输入图像进行颜色空间的标准化（归一化）；目的是调节图像的对比度，降低图像局部的阴影和光照变化所造成的影响，同时可以抑制噪音的干扰；
  (3) 计算图像每个像素的梯度（包括大小和方向）；主要是为了捕获轮廓信息，同时进一步弱化光照的干扰。
  (4) 将图像划分成小cells（例如66像素/cell）；
  (5) 统计每个cell的梯度直方图（不同梯度的个数），即可形成每个cell的特征描述；
  (6) 将每几个cell组成一个block（例如33个cell/block），一个block内所有cell的特征描述串联起来便得到该block的HOG特征descriptor。
  (7) 将图像image内的所有block的HOG特征描述串联起来就可以得到该image（你要检测的目标）的HOG特征描述了。这个就是最终的可供分类使用的特征向量。
  
  

• 代码实现

from skimage import feature as ft
import cv2
image = cv2.imread('muti_person.jpg') 
ori = 5
ppc = (3,3)
cpb = (3,3)
features = ft.hog(image,  # input image
                  orientations=ori,  # number of bins
                  pixels_per_cell=ppc, # pixel per cell
                  cells_per_block=cpb, # cells per blcok
                  block_norm = 'L1', #  block norm : str {‘L1’, ‘L1-sqrt’, ‘L2’, ‘L2-Hys’}, optional
                  transform_sqrt = True, # power law compression (also known as gamma correction)
                  feature_vector=True, # flatten the final vectors
                  visualise=False) # return HOG map
print('the number of HOG features in image is %d'%len(features))

输出结果：

the number of HOG features in image is 1120410

注：此处需要预装skimage的库，否则会报错，安装方法是：

pip install scikit-image

3.1.3 LBP(局部二值模式)
  LBP（Local Binary Pattern）是一种用来描述图像局部纹理特征的算子；它具有旋转不变性和灰度不变性等显著的优点。它是首先由T. Ojala, M.Pietikäinen, 和D. Harwood 在1994年提出，用于纹理特征提取。而且，提取的特征是图像的局部的纹理特征，由于LBP特征计算简单、效果较好，因此LBP特征在计算机视觉的许多领域都得到了广泛的应用，LBP特征比较出名的应用是用在人脸识别和目标检测中。
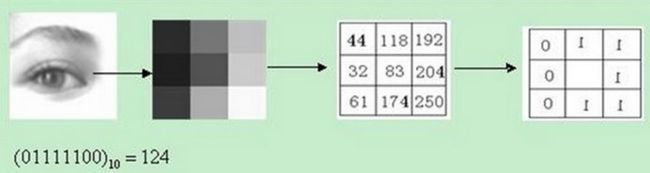
  LBP算子定义在像素33的邻域内，以邻域中心像素为阈值，相邻的8个像素的灰度值与邻域中心的像素值进行比较，若周围像素大于中心像素值，则该像素点的位置被标记为1，否则为0。这样，33邻域内的8个点经过比较可产生8位二进制数，将这8位二进制数依次排列形成一个二进制数字，这个二进制数字就是中心像素的LBP值，LBP值共有$2^8$种可能，因此LBP值有256种。中心像素的LBP值反映了该像素周围区域的纹理信息。

 &emsp由于这个特征的计算是非常简单易懂的，所以不附上它的实现方式。上面讲述的是传统的LBP算子的计算方法，由于原始LBP特征使用的是固定邻域内的灰度值，因此当图像的尺度发生变化时，LBP特征的编码将会发生错误，LBP特征将不能正确的反映像素点周围的纹理信息，因此研究人员对其进行了改进:

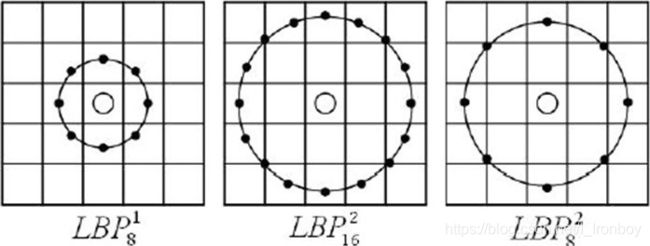
  (1) 将 3×3 邻域扩展到任意邻域，并用圆形邻域代替了正方形邻域，改进后的 LBP 算子允许在半径为 R 的圆形邻域内有任意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个采样点的LBP算子

  (2) 上面的LBP特征具有灰度不变性，但还不具备旋转不变性，因此研究人员又在上面的基础上进行了扩展，提出了具有旋转不变性的LBP特征。首先不断的旋转圆形邻域内的LBP特征，根据选择得到一系列的LBP特征值，从这些LBP特征值选择LBP特征值最小的作为中心像素点的LBP特征。具体做法如下图所示：

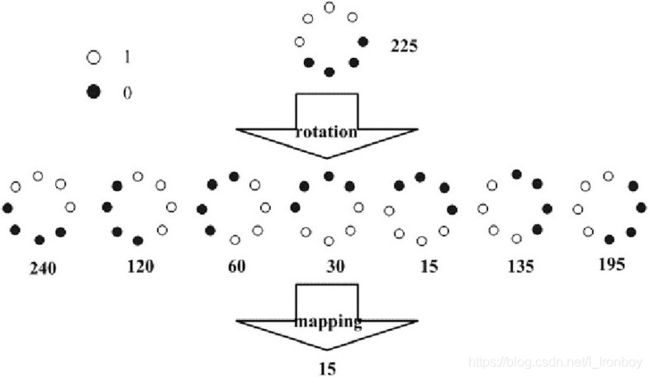
  如图，通过对得到的LBP特征进行旋转，得到一系列的LBP特征值，最终将特征值最小的一个特征模式作为中心像素点的LBP特征。具体实现可参考文章： –Allen–, LBP特征原理

3.1.4 SIFT(尺度不变特征变换匹配算法)
  SIFT，即尺度不变特征变换（Scale-invariant feature transform，SIFT），是用于图像处理领域的一种描述。这种描述具有尺度不变性，可在图像中检测出关键点，是一种局部特征描述子。SIFT特征是基于物体上的一些局部外观的兴趣点而与影像的大小和旋转无关。对于光线、噪声、微视角改变的容忍度也相当高。基于这些特性，它们是高度显著而且相对容易撷取，在母数庞大的特征数据库中，很容易辨识物体而且鲜有误认。
  SIFT算法实现物体识别主要有三大工序，1、提取关键点；2、对关键点附加详细的信息（局部特征）也就是所谓的描述器；3、通过两方特征点（附带上特征向量的关键点）的两两比较找出相互匹配的若干对特征点，也就建立了景物间的对应关系。

1. 通俗理解
     在传统目标检测的任务中，很多情况都是给出一幅包含物体的参考图像，然后在另外一幅同样含有该物体的图像中实现它们的匹配。两幅图像中的物体一般只是二维的旋转和缩放的关系，最多再考虑图像的亮度及对比度的不同。而实际在真实应用中物体都是三维的，比如检测到一辆车的正面和侧面时检测器都能输出car的结果。
   
   

  基于这些条件下要实现物体之间的匹配，SIFT算法的发明者就想到只要找到多于三对物体间的匹配点就可以通过射影几何的理论建立它们的一一对应。首先在形状上物体既有旋转又有缩小放大的变化，如何找到这样的对应点呢？于是他们的想法是首先找到图像中的一些“稳定点”，这些点是一些十分突出的点不会因光照条件的改变而消失，比如角点、边缘点、暗区域的亮点以及亮区域的暗点，既然两幅图像中有相同的景物，那么使用某种方法分别提取各自的稳定点，这些点之间会有相互对应的匹配点，正是基于这样合理的假设，SIFT算法的基础是稳定点。SIFT算法找稳定点的方法是找灰度图的局部最值，由于数字图像是离散的，想求导和求最值这些操作都是使用滤波器，而滤波器是有尺寸大小的，使用同一尺寸的滤波器对两幅包含有不同尺寸的同一物体的图像求局部最值将有可能出现一方求得最值而另一方却没有的情况，但是容易知道假如物体的尺寸都一致的话它们的局部最值将会相同。SIFT的精妙之处在于采用图像金字塔的方法解决这一问题，我们可以把两幅图像想象成是连续的，分别以它们作为底面作四棱锥，就像金字塔，那么每一个截面与原图像相似，那么两个金字塔中必然会有包含大小一致的物体的无穷个截面，但应用只能是离散的，所以我们只能构造有限层，层数越多当然越好，但处理时间会相应增加，层数太少不行，因为向下采样的截面中可能找不到尺寸大小一致的两个物体的图像。有了图像金字塔就可以对每一层求出局部最值，但是这样的稳定点数目将会十分可观，所以需要使用某种方法抑制去除一部分点，但又使得同一尺度下的稳定点得以保存。有了稳定点之后如何去让程序明白它们之间是物体的同一位置？研究者想到以该点为中心挖出一小块区域，然后找出区域内的某些特征，让这些特征附件在稳定点上，SIFT的又一个精妙之处在于稳定点附加上特征向量之后就像一个根系发达的树根一样牢牢的抓住它的“土地”，使之成为更稳固的特征点，但是问题又来了，遇到旋转的情况怎么办？发明者的解决方法是找一个“主方向”然后以它看齐，就可以知道两个物体的旋转夹角了。
  具体原理的讲解可见文章：SIFT特征匹配算法介绍——寻找图像特征点的原理。
2. 代码实现
  实际上该算法如果想完全自己用Python或C++底层实现的话还是非常麻烦的，但目前opencv库已经集成了SIFT关键点提取的功能，需要用到时候直接调库使用即可，其Python的实现方法如下:

import cv2
import numpy as np
# 读取待检测图片
img = cv2.imread('muti_person.jpg') 
# 色彩图灰度化-[0,255]
gray= cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) 
# 创建一个SIFT类
sift = cv2.xfeatures2d.SIFT_create() 
# 找到关键点
kp = sift.detect(gray,None)
# 绘制关键点
img=cv2.drawKeypoints(gray,kp,img)
cv2.imshow('SIFT points',img)
cv2.waitKey(0)

结果展示：左边原图，右边显示关键点的图

  在我本人实现的过程中出现了两个小问题，解决方法如下：如果cv2报错没找到xfeatures2d的库，那么是因为opencv3.X以后OpenCv只包含部分内容，需要神经网络或者其他的函数需要导入opencv_contrib，具体方法是pip install opencv_contrib，但是当装完这个库之后又会出现如下报错

  我在网上找了问题之后发现貌似因为该算法被申请了专利或其他原因，只要将opencv版本退到3.4.2即可解决，卸载之前的包，即在命令行窗口输入pip install opencv_python==3.4.2.16和pip install opencv-contrib-python==3.4.2.16(吐槽一下pip 安装巨慢，不过听说在该行代码后面添加别的源镜像网站可以加快下载速度，不过我真的是懒得搞了！)

3.1.5 SURF(加速稳健特征)
  SURF(Speeded Up Robust Features, 加速稳健特征) 是一种稳健的图像识别和描述算法。它是SIFT的高效变种，也是提取尺度不变特征，算法步骤与SIFT算法大致相同，但采用的方法不一样，要比SIFT算法更高效（正如其名）。由于算法步骤大致相同，我们重点讲讲区别和改进之处。
  (1) SIFT算法建立一幅图像的金字塔，在每一层进行高斯滤波并求取图像差(DOG)进行特征点的提取，而SURF则用的是Hessian矩阵进行特征点的提取，所以Hessian矩阵是SURF算法的核心;
  (2) 在尺度空间构造中，SIFT算法的同一个层中的图片大小相同，但是模糊程度不同，而不同的层中的图片大小也不相同，因为它是由上一层图片降采样得到的。在进行高斯模糊时，SIFT的高斯模板大小是始终不变的，只是在不同的层之间改变图片的大小。而在SURF中，图片的大小是一直不变的，不同的层得到的待检测图片是改变高斯模糊尺寸大小得到的，当然了，同一个层中个的图片用到的高斯模板尺度也不同。算法允许尺度空间多层图像同时被处理，不需对图像进行二次抽样，从而提高算法性能。

  (3) 为了保证旋转不变性，在SURF中，不统计其梯度直方图，而是统计特征点领域内的Harr小波特征。即以特征点为中心，计算半径为6s(S为特征点所在的尺度值)的邻域内，统计60度扇形内所有点在x(水平)和y(垂直)方向的Haar小波响应总和(Haar小波边长取4s)，并给这些响应值赋高斯权重系数，使得靠近特征点的响应贡献大，而远离特征点的响应贡献小，然后60度范围内的响应相加以形成新的矢量，遍历整个圆形区域，选择最长矢量的方向为该特征点的主方向。这样，通过特征点逐个进行计算，得到每一个特征点的主方向。该过程的示意图如下:

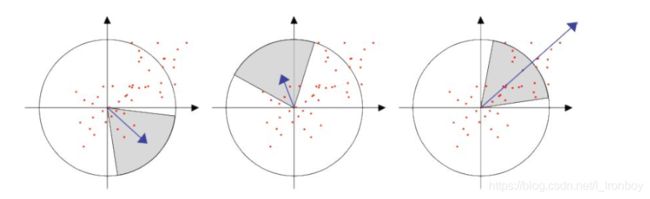
  由于SURF是SIFT的一个变种加速版本，基本原理很相似，故不继续细讲，想自主实现仔细了解的同学可参考文章 图像特征— —SURF特征

3.3 分类器

  在传统的目标检测与识别算法中，最后都是用一个分类器来判别候选框中的物体是属于哪一个类别，以完成识别的任务，而一般常用的就是支持向量机SVM、Adaboost和决策树这三种分类器，由于网上对这三种分类器详细讲解和相关练习题资料很多，此处我就简述一下自己的想法。。
3.3.1 支持向量机SVM
  支持向量机的思想很简单，但是实际的计算却是挺麻烦的。单纯谈支持向量都是针对二分类问题，问题描述如下：给定训练样本集$D=(x_1,y_1),(x_2,y_2),...,(x_m,y_m),y_i\in -1,1$，希望在该样本空间中找到一个划分超平面，将不同类别的样本分开。

  显然，能将样本分开的超平面有很多种，但直观上看，应该去找位于两类训练样本“正中间”的划分超平面，即上图中红色的那个，因为该划分超平面对训练样本局部扰动的“容忍”性最好，专业说法就是：这个划分超平面所产生的分类结果是最鲁棒的，对未见示例的泛化能力最强。这里引入了两个个概念——“支持向量”和“间隔”(margin)。
支持向量和间隔
  假设超平面$(w,b)$能将训练样本正确分类，即对于$(x_i,y_i)\in D$，若$y_i=+1$，则有$w^T{x}_i+b>0$；若$y_i=-1$，则有$w^T{x}_i+b<0$，但其实每个类别里面的点到分类超平面都有一个最小距离，而按照上面“正中间的概念”来描述就是每个类别里面的点到分类超平面都有一个最小距离，且两个最小距离相等，于是我们可以调整$(w,b)$的相对大小，使得这个最小距离正好等于1，其实此处不是说必须只能等于1，等于多少都可以，只是一个为了之后的计算做了个约束，1是个比较简单的数字，就用1了，那么重新描述一下就是：对于这个能将训练样本正确分类的超平面$(w,b)$，每个类别里面的点到分类超平面都有一个最小距离，且两个最小距离相等均为1，并且满足$w^T+b=1，y_i=+1$和$w^T+b=-1,y_i=-1$的那些训练样本成为支持向量，两个类别的支持向量到分类超平面的距离之和为$\gamma =\frac{2}{w}$，这就是间隔margin，之后的计算问题就是如何找到这个$(w,b)$，这个可以表示成一个约束问题，通过转换为对偶问题，利用拉格朗日乘数法可以解决。
一些额外的思考
  最开始学SVM支持向量机的时候，看到周志华老师西瓜书上写的那句话

直观上看，应该去找位于两类训练样本“正中间”的划分超平面，即图中红色的那个，因为该划分超平面对训练样本局部扰动的“容忍”性最好

  我是有些异议的，因为我感觉这个直观上的想法忽视了数据本身的分布，即只考虑了离分类超平面最近的那几个点，其他点只要是没有越过这个界限是可以随意分布的，反正最后的超平面的计算跟他们也没有什么关系。即以下的两种情况最后得到的最优的分类超平面是一样的。

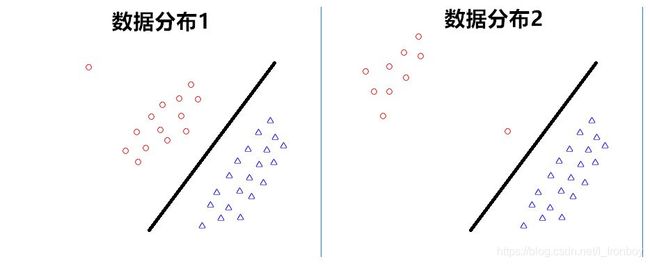
  那么我就想，支持向量机得到的结果并没有完全考虑数据的一个分布，即没有充分利用数据的信息，那么他最后得到结果的抗干扰能力是不是其实没有提升到最大。我的想法是：找到一个超平面$(w,b)$，这个超平面到每个点都有一个垂直距离d，那么这个间隔margin可不可以定义为所有点到这个垂直距离之和最小，那么所有点的数据都用上了(那么这里其实就失去了支持向量这个概念)，像上图的那个情况，分布2的分类超平面应该往上再挪一点，因为根据数据分布，计算上认为红点的数据大部分都在远离分类平面的地方，而蓝色的点在更靠近分类平面的地方，为了提升对未知数据的泛化能力，分类平面不会在两者正中间，而是稍微偏向上面的地方。这是我学习SVM时候的一些额外的思考，但是并没有进行深入的推导，因为数学层面上确实很麻烦，且有过拟合的嫌疑。如果读者看到相似的思考和解释，希望能提醒我一下，将感激不尽。
3.3.2 Adaboost
  Adaboost是集成学习中Boosting系列算法中最著名的代表。集成学习的思想就是通过构建并结合多个学习器来完成学习任务。这多个学习器一般针对弱学习器，通过结合多个弱分类器。常可获得比单一学习器显著优越的泛化性能。举个例子就是，有个实验班有两类人，一类是非常全面的学霸，各个科目的考试都能考到95；另外还有一类人是偏科生，当年分别凭着数学竞赛、物理竞赛、生物化学竞赛、写作比赛、英语竞赛等等单科竞赛得了很好的奖才进的这个班，他们有个特点就是优势学科经常能考到99甚至100，但是弱势科目总是在及格线上徘徊，所以总的分数肯定是不及全面发展的学霸。那么集成学习就是让这些偏科的同学组成一个团队去和这个学霸竞争考试，结果会是怎么样呢？显然，由偏科同学组成的超级天团能够在各科上取得99或100这样接近满分的成绩，总分也是接近满分，但是学霸也还是均分95，虽然也是超级优秀，但跟这个天团相比还是差很多。这个思想就可以运用到集成学习中，这些偏科同学其实就是一个个弱学习器，组成的天团就是强学习器。因为在实际的机器学习算法应用过程中，要训练一个非常好的能满足要求的强学习器是及极其困难的，但是训练一群弱学习器相比之下还是很好得到的，只是这些弱分类器有个要求，不能完全相同，否则一个和两个其实没有任何意义。
  接下来讲讲Boosting的基本思想：先从初始训练集训练一个基学习器，再根据基学习器的表现对训练样本分布进行调整，使得先前基学习器做错的样本在后续受到更多的关注，然后基于调整后的样本分布来训练下一个基学习器，如此重复进行，直至基学习器数目到达事先指定的值T，最终将这T个基学习器进行加权结合。接下来解释一下西瓜书上的Adaboost流程

  首先过程1是一个初始化的过程，在最开始的时候由于还没有进行学习，所以假定数据集里每个数据的分布是均匀的，即$1/m$，然后从第2步-第7步是一个for语句，经过T次学习，得到T个学习器。让我们看看for语句的内部，第t轮的学习首先是根据给定的训练集$D$和当前数据集的数据分布$D_T$，按照给定的基学习算法训练得到一个学习器$h_t$，然后计算这个学习器在目前训练集上的一个错误率${ϵ}_t$，如果错误率大于0.5，即都没能达到随机瞎猜的能力那么就跳出循环，证明此次学习是失败的，具体怎么改进重启可以自行百度了解，这里只讲基本原理；如果错误率小于0.5，那么证明这次训练得到的学习器是可以有一定能力的，于是第六步是计算该分类器在之后分类器线性加权结合的时候应该占的权重，具体这样计算的原因可以参照书本的公式推导，还是挺详细的。得到权重后接着计算下一次训练集的数据分布，可以从第七步看到分对的数据权重是$exp(-{\alpha }_t)$，小于1，分错的数据权重是$exp({\alpha }_t)$，大于1，$Z_t$是一个归一化的因子，按照之前Boosting的基本思路，每次训练后调整权重是为了使得这次分错的样本在后续的学习中得到更大的关注。如此训练T次，之后输出一个T个弱学习器线性加权的强分类器。
3.3.3 决策树
  决策树是一种树形结构，其中每个内部节点表示一个属性上的测试，每个分支代表一个测试输出，每个叶节点代表一种类别。我们这里要讲的是决策分类树，核心思想就是在一个数据集中找到一个最优特征，然后从这个特征的选值中找一个最优候选值(这段话稍后解释)，根据这个最优候选值将数据集分为两个子数据集，然后递归上述操作，直到满足指定条件为止。

• 决策树的构建
     决策树构建的本质就是在选择属性，即每次选择什么样的属性来对样本进行分类。ID3算法用的是信息增益，C4.5算法用信息增益率；CART算法使用基尼系数。决策树方法是会把每个特征都试一遍，然后选取那个能够使分类分的最好的特征，也就是说将A属性作为父节点，产生的信息增益（GainA）要大于B属性作为父节点，则A作为优先选取的属性。上面谈到的“信息增益”又需要提到信息熵这个概念——信息的混乱程度，因为决策树不断分而治之的过程是一个熵减小的过程，即同一个分类集合里数据的相似性越来越高。
  1. ID3算法：信息增益计算
  $info(D)=-{\sum }_{i=1}^m{p}_{i}lo{g}_2{p}_i$
  $inf{o}_A(D)=-{\sum }_{j=1}^v\frac{|D_j|}{|D|}\times info(D_j)$
  $Gain(D,A)=info(D)-inf{o}_A(D)$
  2. C4.5算法：信息增益率计算
  $Gai{n}_{r}atio(D,A)=\frac{Gain(D,A)}{IV(a)}$
  其中IV(a)为属性A的固有值：$IV(a)=-{\sum }_{v=1}^V\frac{|D_v|}{|D|}lo{g}_2\frac{|D_v|}{|D|}$，属性a的可能取值数目越多，则IV(a)的值越大，这样通过引入约束项，可以从一定程度上削弱“对取值多的属性”的偏好，但是同时增益率准则对可取值数目较少的属性有所偏好。
  3. CART算法：基尼系数计算
    CART决策树使用“基尼指数”(Gini index)来选择划分属性，数据集D的纯度可以用基尼值来度量：
  $Gini(D)={\sum }_{k=1}^{|y|}{\sum }_{k^{\prime }\ne k}{p}_k{p}_{k^{\prime }}=1-{\sum }_{k=1}^{|y|}{p}_k^2$
    直观上的理解为，Gini(D)反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率。因此，Gini(D)越小，则数据集D纯度越高。于是产生了基尼指数(Gini index)：
  $GiniIndex(D,A)={\sum }_{v=1}^V\frac{|D_v|}{|D|}Gini(D^v)$
    于是可以选择使得基尼指数最小的属性作为最优化分属性。
• 剪枝
    剪枝(pruning)是解决决策树过拟合的主要手段，通过剪枝可以大大提升决策树的泛化能力。通常，剪枝处理可分为：预剪枝，后剪枝。
    预剪枝：通过启发式方法，在生成决策树过程中对划分进行预测，若当前结点的划分不能对决策树泛化性能提升，则停止划分，并将其标记为叶节点
    后剪枝：对已有的决策树，自底向上的对非叶结点进行考察，若该结点对应的子树替换为叶结点能提升决策树的泛化能力，则将改子树替换为叶结点
    对于后剪枝策略，可以通过极小化决策树整体的损失函数(Cost function)来实现。设树T的叶节点个数为|T|，t是树T的叶结点，该叶节点有Nt个样本点，其中k类的样本点有Ntk个，k=1,2,…,K，Ht(T)为叶结点t上的经验熵，α≥0为参数，则决策树学习的损失函数可以定义为：
  $C_{\alpha }(T)={\sum }_{t=1}^T{N}_t{H}_t(T)+\alpha (t)$
    其中经验熵H(t)为：
  $H(t)=-{\sum }_k\frac{N_{tk}}{N_t}log\frac{N_{tk}}{N_t}$
    令C(T)表示模型对训练数据预测误差，即模型与训练数据的拟合程度，|T|表示模型的复杂度，参数α≥0调节二者关系。
    模型对训练数据预测误差:
  $C(T)={\sum }_{t=1}^T{N}_t{H}_t(T)=-{\sum }_{t=1}^T{\sum }_{k=1}^K{N}_{tk}log\frac{N_{tk}}{N_t}$
    这时损失函数变为：
  $C_{\alpha }(T)=C(T)+\alpha (t)$
    较大的α促使树的结构更简单，较小的α促使树的结构更复杂，α=0意味着不考虑树的复杂度（α|T|就是正则项，加入约束，使得模型简单，避免过拟合）。
    损失函数认为对于每个分类终点（叶子节点）的不确定性程度就是分类的损失因子，而叶子节点的个数是模型的复杂程度，作为惩罚项，损失函数的第一项是样本的训练误差，第二项是模型的复杂度。如果一棵子树的损失函数值越大，说明这棵子树越差，因此我们希望让每一棵子树的损失函数值尽可能得小，损失函数最小化就是用正则化的极大似然估计进行模型选择的过程。
    决策树的剪枝过程（泛化过程）就是从叶子节点开始递归，记其父节点将所有子节点回缩后的子树为$T_b$（分类值取类别比例最大的特征值），未回缩的子树为$T_a$，如果$C_{\alpha }(T_a)\ge C_{\alpha }(T_b)$，说明回缩后使得损失函数减小了，那么应该使这棵子树回缩，递归直到无法回缩为止，这样使用“贪心”的思想进行剪枝可以降低损失函数值，也使决策树得到泛化。
    可以看出，决策树的生成只是考虑通过提高信息增益对训练数据进行更好的拟合，而决策树剪枝通过优化损失函数还考虑了减小模型复杂度。
  公式$C_{\alpha }(T)=C(T)+\alpha |T|$定义的损失函数的极小化等价于正则化的极大似然估计。

3.4 经典的检测算法

3.2.3 Harr特征+Adaboost算法进行人脸检测
  这部分可以参照之前大三我选修的《模式识别》课程的实验作业——基于 Adaboost 的人脸检测系统的设计与实现(opencv+Python)，当时用Python+opencv库做了个简单的人脸识别与跟踪，效果看起来还可以。
3.2.4 Hog特征+Svm算法
  将HOG特征(方向梯度直方图)和支持向量机算法结合起来进行物体检测是传统检测里比较经典的搭配，由于其思路比较简单，直接讲流程吧：
  Step1：获取正样本集并用hog计算特征得到hog特征描述子。例如进行行人检测，可用IRINA等行人样本集，提取出行人的描述子。
  Step2：获取负样本集并用hog计算特征得到hog特征描述子。 负样本图像可用不含检测目标的图像随机剪裁得到。 通常负样本数量要远远大于正样本数目。
  Step3: 利用SVM训练正负正负样本，得到model。
  Step4：利用model进行负样本难例检测。对Training set 里的负样本进行多尺度检测，如果分类器误检出非目标则截取图像加入负样本中。(hard-negative mining)
  Step5: 结合难例重新训练model。
  Step6：应用最后的分类器model检测test set，对每幅图像的不同scale进行滑动扫描，提取descriptor并用分类器做分类。如果检测为目标则用bounding box 框出。图像扫描完成后应用 non-maximum suppression 来消除重叠多余的目标。
  注意：我们用的HOG特征提取窗一般大小固定，但是实际照片里面物体跟照相机的远近不同物体大小的显示也是不同的，所以为了克服这个问题，实际操作中，可以使得特征提取窗口大小不变，但是将图片放大缩小到多个分辨率上进行检测，就可以发现不同位置，不同大小的物体了。
3.2.5 DPM算法
  DPM（Deformable Part Model），正如其名称所述，可变形的组件模型，是一种基于组件的检测算法，其所见即其意。它是一个非常成功的目标检测算法，连续获得VOC（Visual Object Class）07,08,09年的检测冠军。目前已成为众多分类器、分割、人体姿态和行为分类的重要部分。2010年Pedro Felzenszwalb被VOC授予"终身成就奖"。DPM可以看做是HOG（Histogrrams of Oriented Gradients）的扩展，大体思路与HOG一致。先计算梯度方向直方图，然后用SVM（Surpport Vector Machine ）训练得到物体的梯度模型（Model）。有了这样的模板就可以直接用来分类了，简单理解就是模型和目标匹配。
  DPM只是在模型上做了很多改进工作。传统的HOG特征只采用一个模板表示某种物体，而DPM把物体的模板划分成根模型和部分模型，其中的根模型等效于传统的HOG特征，部分模型则是物体某些部分的模板。在检测的时候，根模型用来对物体可能存在的位置进行定位，部分模型用来进行进一步的确认。付出了更多的运算量使得DPM的检测效果要优于传统的HOG。

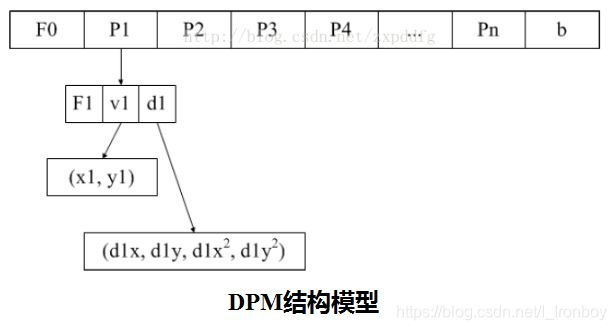
算法思想：

1. 根滤波器+组件滤波器
2. 响应值的计算
3. DPM特征定义
4. DPM检测流程
5. Latent SVM

致歉： 由于我之后的工作重心是在深度学习方面，所以这部分的DPM算法没有很具体地去搞懂，只明白个大致思路，不敢继续往下写了。其实网上的很多资料说的也都不清楚，真正想学透的还是看当年发表的论文吧。至于实现的话，opencv都有相应的库，不需要从底层自己一步一步搭建，还是比较友好的。

该篇参考文献

【1】 专丶注, 目标检测之滑动窗口与选择搜索的比较
【2】 –Allen–, LBP特征原理
【3】Sin_Geek, 图像特征— —SURF特征
【4】千万里不及你, 决策树(ID3 & C4.5 & CART)
【5】确定有穷自动机, 利用hog+svm（梯度方向直方图和支持向量机）实现物体检测
【6】zxpddfg, Deformable Parts Model (DPM) 简介
【7】TTransposition, DPM(Deformable Parts Model)–原理(一)
【8】watersink, DPM（Deformable Part Model）原理详解