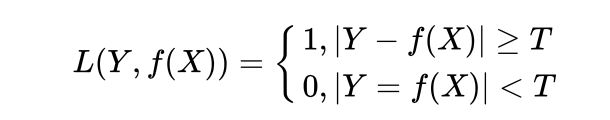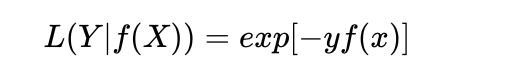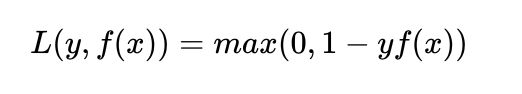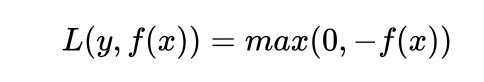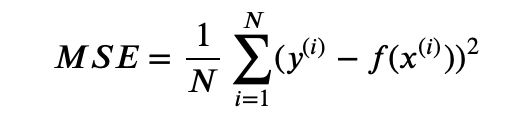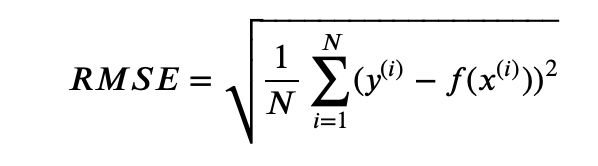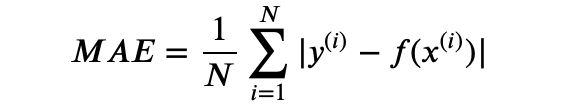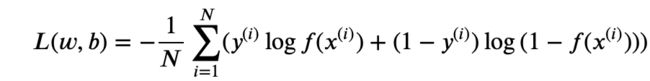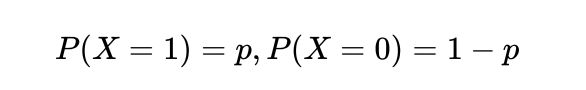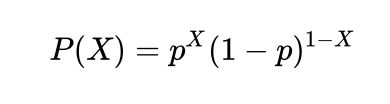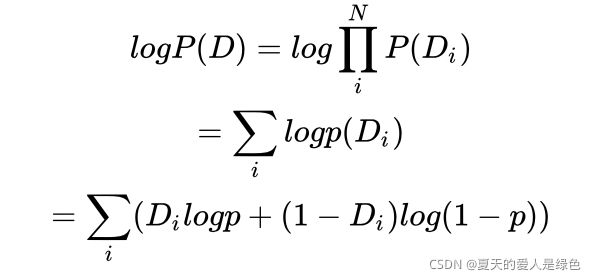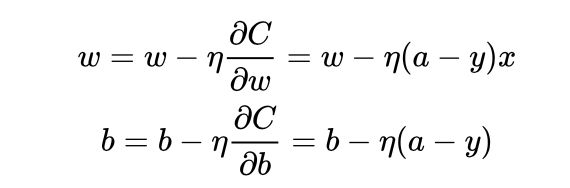损失函数与代价函数

往期文章推荐：
    脉冲神经网络资料汇总
   神经网络从入门到精通

---

【版权申明】未经博主同意，谢绝转载！（请尊重原创，博主保留追究权）；

本博客的内容来自于：损失函数与代价函数；

学习、合作与交流联系q384660495；

本博客的内容仅供学习与参考，并非营利；

---

一、 损失函数、代价函数与目标函数

损失函数（Loss Function）：是定义在单个样本上的，是指一个样本的误差。
代价函数（Cost Function）：是定义在整个训练集上的，是所有样本误差的平均，也就是所有损失函数值的平均。
目标函数（Object Function）：是指最终需要优化的函数，一般来说是经验风险+结构风险，也就是（代价函数+正则化项）。

二、常见的损失函数

1. 0-1损失函数(0-1 loss function)

L(Y,f(X))={1,Y≠f(X) or 0,Y=f(X)}

可以看出，该损失函数的意义就是，当预测错误时，损失函数值为1，预测正确时，损失函数值为0。

该损失函数不考虑预测值和真实值的误差程度，也就是只要预测错误，预测错误差一点和差很多是一样的。
0-1损失函数直接对应分类判断错误的个数，但是它是一个非凸函数，不太适用.
感知机就是用的这种损失函数。但是相等这个条件太过严格，因此可以放宽条件，即满足 如下公式 时认为相等

2. 平方损失函数(quadratic loss function)

L(Y,f(X))=(Y−f(X))^2

该损失函数的意义也很简单，就是取预测差距的平方。

3. 绝对值损失函数(absolute loss function)

L(Y,f(X))=|Y−f(X)|

该损失函数的意义和上面差不多，只不过是取了绝对值而不是求绝对值，差距不会被平方放大。

4. 对数损失函数(logarithmic loss function)

L(Y,P(Y|X))=−logP(Y|X)

这个损失函数就比较难理解了。事实上，该损失函数用到了极大似然估计的思想。P(Y|X)通俗的解释就是：在当前模型的基础上，对于样本X，其预测值为Y，也就是预测正确的概率。由于概率之间的同时满足需要使用乘法，为了将其转化为加法，我们将其取对数。最后由于是损失函数，所以预测正确的概率越高，其损失值应该是越小，因此再加个负号取个反。

(1) log对数损失函数能非常好的表征概率分布，在很多场景尤其是多分类，如果需要知道结果属于每个类别的置信度，那它非常适合。
(2)健壮性不强，相比于hinge loss对噪声更敏感。
(3)逻辑回归的损失函数就是log对数损失函数。

5. 指数损失函数（exponential loss）

特点：

(1)对离群点、噪声非常敏感。经常用在AdaBoost算法中。

6. Hinge 损失函数

特点：

(1)hinge损失函数表示如果被分类正确，损失为0，否则损失就为 [公式] 。SVM就是使用这个损失函数。

(2)一般的 [公式] 是预测值，在-1到1之间， [公式] 是目标值(-1或1)。其含义是， [公式]
的值在-1和+1之间就可以了，并不鼓励 [公式]
，即并不鼓励分类器过度自信，让某个正确分类的样本距离分割线超过1并不会有任何奖励，从而使分类器可以更专注于整体的误差。

(3) 健壮性相对较高，对异常点、噪声不敏感，但它没太好的概率解释。

7. 感知损失(perceptron loss)函数

特点：

(1)是Hinge损失函数的一个变种，Hinge loss对判定边界附近的点(正确端)惩罚力度很高。而perceptron
loss只要样本的判定类别正确的话，它就满意，不管其判定边界的距离。它比Hinge loss简单，因为不是max-margin
boundary，所以模型的泛化能力没 hinge loss强。

常见的代价函数

1. 均方误差（Mean Squared Error）
   

均方误差是指参数估计值与参数真值之差平方的期望值; MSE可以评价数据的变化程度，MSE的值越小，说明预测模型描述实验数据具有更好的精确度。通常用来做回归问题的代价函数。

2. 均方根误差
   

均方根误差是均方误差的算术平方根，能够直观观测预测值与实际值的离散程度。通常用来作为回归算法的性能指标。

3. 平均绝对误差（Mean Absolute Error）
   

平均绝对误差是绝对误差的平均值 ，平均绝对误差能更好地反映预测值误差的实际情况。通常用来作为回归算法的性能指标。

4. 交叉熵代价函数（Cross Entry）
   

交叉熵是用来评估当前训练得到的概率分布与真实分布的差异情况，减少交叉熵损失就是在提高模型的预测准确率。其中 ()是指真实分布的概率， q(x) 是模型通过数据计算出来的概率估计。
比如对于二分类模型的交叉熵代价函数（可参考逻辑回归一节）：

其中 ()可以是sigmoid函数。或深度学习中的其它激活函数。而 ()∈0,1。

相关高频问题：

1.交叉熵函数与最大似然函数的联系和区别？

区别：交叉熵函数使用来描述模型预测值和真实值的差距大小，越大代表越不相近；似然函数的本质就是衡量在某个参数下，整体的估计和真实的情况一样的概率，越大代表越相近。

联系：交叉熵函数可以由最大似然函数在伯努利分布的条件下推导出来，或者说最小化交叉熵函数的本质就是对数似然函数的最大化。

怎么推导的呢？我们具体来看一下。

设一个随机变量X满足伯努利分布，

则X 的概率密度函数为：

因为我们只有一组采样数据 D，我们可以统计得到X和1-X的值，但是 p的概率是未知的，接下来我们就用极大似然估计的方法来估计这个p值。

对于采样数据 D，其对数似然函数为:

可以看到上式和交叉熵函数的形式几乎相同，极大似然估计就是要求这个式子的最大值。而由于上面函数的值总是小于0，一般像神经网络等对于损失函数会用最小化的方法进行优化，所以一般会在前面加一个负号，得到交叉熵函数（或交叉熵损失函数）：

这个式子揭示了交叉熵函数与极大似然估计的联系，最小化交叉熵函数的本质就是对数似然函数的最大化。

现在我们可以用求导得到极大值点的方法来求其极大似然估计，首先将对数似然函数对 [公式] 进行求导，并令导数为0，得到

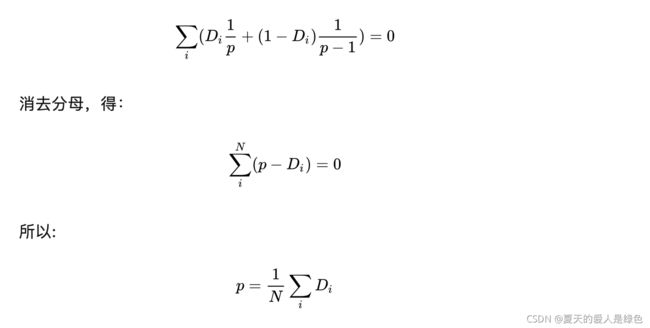
这就是伯努利分布下最大似然估计求出的概率 [公式] 。

2. 在用sigmoid作为激活函数的时候，为什么要用交叉熵损失函数，而不用均方误差损失函数？

其实这个问题求个导，分析一下两个误差函数的参数更新过程就会发现原因了。

因为sigmoid的性质，导致 [公式] 在 [公式] 取大部分值时会很小（如下图标出来的两端，几乎接近于平坦），这样会使得 [公式] 很小，导致参数 [公式] 和 [公式] 更新非常慢。

可以看到参数更新公式中没有 [公式] 这一项，权重的更新受 [公式] 影响，受到误差的影响，所以当误差大的时候，权重更新快；当误差小的时候，权重更新慢。这是一个很好的性质。

所以当使用sigmoid作为激活函数的时候，常用交叉熵损失函数而不用均方误差损失函数。