tensorflow学习笔记【搭建神经网络】
Tensorflow学习笔记之搭建神经网络
一、 神经网络参数
神经网络的参数是指神经元线上的权重W, 用变量表示, 一般会随机生成这些参数。生成这些参数的方法是tf.Variable, 把生成的方式写在括号中。
常用的神经网络函数有:
tf.random_normal() 生成正态分布随机数
tf.truncated_normal() 生成去掉过大偏移点的正态分布随机数
tf.random_uniform() 生成均匀分布随机数
tf.zeros 表示生成全0 的数组
tf.ones 表示生成全1 的数组
tf.fill 表示生成全定值的数组
tf.constant 表示生成直接给定值的数组
二、 神经网络的搭建
当我们知道张量,计算图,会话和参数后,我们可以讨论神经网络的实现过程了。
神经网络的实现过程:
1、 准备数据集,提取特征,作为输入喂给神经网络
2、 搭建NN结构, 从输入到输出(先搭建计算图,再用会话执行)
3、大量特征数据喂给NN, 迭代优化NN参数
4、使用训练好的模型预测和分类
由此可见,基于神经网络的机器学习主要分为两个过程,即训练过程和使用过程。 训练过程是第一步、第二步、第三步的循环迭代,使用过程是第四步,一旦参数优化完成就可以固定这些参数,实现特定的应用了。
很多实际的应用中,我们会实现使用现有的网络结构,喂入新的数据,训练相应的模型,判断能否对未入的新数据做出正确响应,在适当更改网络结构,反复迭代,在机器能够自动训练参数找出最优的结构和参数,以固定专用模型。
三、 前向传播
前向传播就是搭建模型的计算过程,让模型具有推理能力,可以针对一对输入数据给出相应的输出结果。
前向传播过程的tensorflow描述:
变量初始化,计算图节点运算都用session会话来实现
with tf.Session() as sess:
sess.run()
变量初始化: 在sess.run() 函数中用tf.global_variables_initializer() 汇总所有待优化的变量
init_op = tf.global_variable_initializer()
sess.run(init_op)
用tf.placeholder 占位, 在sess.run 函数中用feed_dict 喂数据
x = tf.placeholder(tf.float32, shape = (1,2))
sess.run(y,feed_dict={x:[0.5, 0.6]})
举例:
这是一个实现神经网络前向传播的过程,网络可以自动推理出输出y的值
1、用placeholder 实现输入定义(sess.run() 中喂入一组数据)的情况
import tensorflow as tf
#定义输入和参数
x = tf.placeholder(tf.float32,shape = (1,2))
w1 = tf,Variable(tf.random_normal([2,3], stddev = 1, seed = 1))
w2 = tf.Variable(tf.random_normal([3,1], stdden = 1, seed = 1))
#定义前向传播过程
a = tf.matmul(x,w1)
y = tf.matmul(a,w2)
#用会话计算结果
with tf.Session() as sess:
init_op = tf.global_variable_initilizer()
sess.run(init_op)
print ("y:\n", sess.run(y,feed_dict = {x:[0.7,0.5],[0.2,0.3],[0.3,0.4],[0.4,0.5]}))
三、 反向传播
1、反向传播: 训练模型参数,在所有参数上使用梯度下降,使得NN模型在训练数据上的损失函数最小。
2、损失函数: 计算得到的预测值y与真实值之间的差距
损失函数有多种计算方法,MSE是最常用的方法。
3、均方误差: 求前向传播计算结果与真实结果之差的再求平均
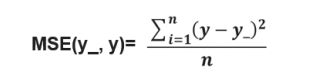
用tensorflow函数表示为:
loss_mse = tf.reduce_mean(tf.square(y_ - y))
反向传播训练方法: 以减少loss为优化目标,有梯度下降、momentum优化器,adam优化器等方法。
这三种方法用tensorlfow函数实现可以表示为:
train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
train_step = tf.train.MomentumOptimizer(learning_rate).minimizer(loss)
train_step = tf.train.AdamOptimzer(learning_rate).minimizer(loss)
4、 学习率
优化器中需要一个叫做学习率的参数,使用时,如果学习概率选择过大则会出现震荡不收敛的情况,如果选择太小,会出现收敛缓慢的情况,所以在填写的过程中我们一般会选择使用, 0.01, 0.001
5、 进阶 (反向传播过程中的参数推导过程)
四、 搭建神经网络的八股
神经网络的搭建主要分四步完成: 准备工作,前向传播,反向传播和循环迭代
1、 导入模块: 生成模拟数据集
2、前向传播: 定义输入、参数和输出
3、 反向传播: 定义损失函数、反向传播方法
4、 生成会话: 悬链step轮
with tf.Session() as tf:
init_op = tf.global_variable_initilizer()
sess.run(init_op)
STEP = 300
for i in range(STEP):
start =
end =
sess.run(train_step, feed_dict:)
五、 实例代码
import tensorflow as tf
import numpy as np
batch_size = 8
seed = 23455
rng = np.random.RandomState(seed)
X = rng.rand(32,2)
Y = [[int(x0+x1<1)] for [x0,x1] in X]
print ("X:\n",X)
print ("Y: \n",Y)
#定义神经网络的输入,参数和输出,定义前向传播过程
x = tf.placeholder(tf.float32, shape=(None,2))
y_ = tf.placeholder(tf.float32,shape=(None,1))
w1 = tf.Variable(tf.random_normal([2,3],stddev = 1, seed = 1))
w2 = tf.Variable(tf.random_normal([3,1],stddev = 1, seed = 1))
a = tf.matmul(x,w1)
y = tf.matmul(a,w2)
#定义反向传播函数以及损失函数
loss = tf.reduce_mean(tf.square(y - y_))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss)
#生成会话,训练steps 轮数
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
#输出当前未经训练的数据
print ("W1:\n", sess.run(w1))
print ("W2: \n", sess.run(w2))
#训练模型
STEPS = 3000
for i in range(STEPS):
start = (i*batch_size) %32
end = start + batch_size
sess.run(train_step, feed_dict = {x:X[start:end],y_:Y[start:end]})
if i%500 == 0:
total_loss = sess.run(loss,feed_dict={x:X, y_:Y})
print("After %d training_step(s),loss on all data is %g"%(i,total_loss))
#输出训练后的参数取值
print("\n")
print("w1: \n",sess.run(w1))
print("w2: \n",sess.run(w2))
训练结果:
W1:
[[-0.8113182 1.4845988 0.06532937]
[-2.4427042 0.0992484 0.5912243 ]]
W2:
[[-0.8113182 ]
[ 1.4845988 ]
[ 0.06532937]]
After 0 training_step(s),loss on all data is 5.13118
After 500 training_step(s),loss on all data is 0.429111
After 1000 training_step(s),loss on all data is 0.409789
After 1500 training_step(s),loss on all data is 0.399923
After 2000 training_step(s),loss on all data is 0.394146
After 2500 training_step(s),loss on all data is 0.390597
w1:
[[-0.7000663 0.9136318 0.08953571]
[-2.3402493 -0.14641267 0.58823055]]
w2:
[[-0.06024267]
[ 0.91956186]
[-0.0682071 ]]
Process finished with exit code 0

