数据挖掘实战（3）——时间序列预测ARIMA模型（附踩坑日志）

1 导包

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.stattools import adfuller as ADF
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.tsa.arima_model import ARIMA

2 数据准备

# Seaborn设置
sns.set(style='darkgrid', color_codes=True)  # 设置背景

# Matplotlib设置
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False

df = pd.read_excel('../data/shop.xlsx', index_col='日期')

3 可视化

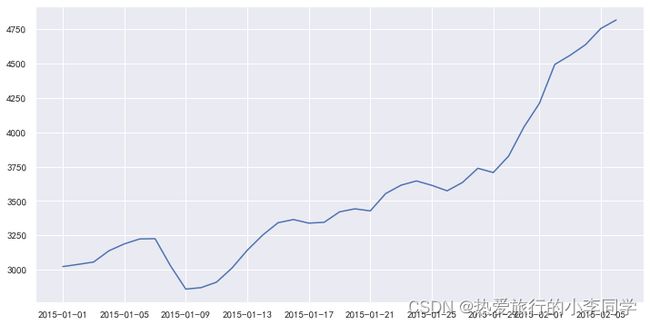
时序图

# 折线图
plt.figure(figsize=(12, 6))
plt.plot(df)
plt.show()

自相关图&平稳性检验
自相关

统计相关性总结了两个变量之间的关系强度。我们可以假设每个变量的分布都符合高斯(钟形曲线)分布。如果是这样，我们可以使用皮尔逊相关系数（Pearson
correlation coefficient）来总结变量之间的相关性。

皮尔逊相关系数是-1和1之间的数字分别描述负相关或正相关。值为零表示无相关。

我们可以使用以前的时间步长来计算时间序列观测的相关性。由于时间序列的相关性与之前的相同系列的值进行了计算，这被称为序列相关或自相关。

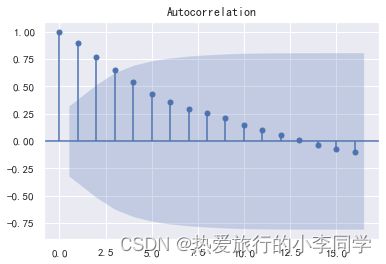
一个时间序列的自相关系数被称为自相关函数，或简称ACF。这个图被称为相关图或自相关图。

# 自相关图
plot_acf(df)
plt.show()
# 自相关系数长期大于零，说明时间序列有很强的相关性

# 平稳性检验
print('原始序列的ADF检验结果为:\n', ADF(df['销量']))

原始序列的ADF检验结果为:
 (1.8137710150945274, 0.9983759421514264, 10, 26, {'1%': -3.7112123008648155, '5%': -2.981246804733728, '10%': -2.6300945562130176}, 299.46989866024177)

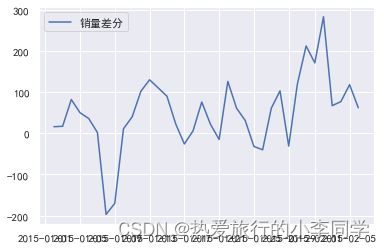
差分时序图

# 1阶差分
d_data = df['销量'].diff().dropna()
d_data.columns = ['销量差分']
plt.plot(d_data, label='销量差分')
plt.legend(loc='best')
plt.show()

差分自相关图&平稳性检验

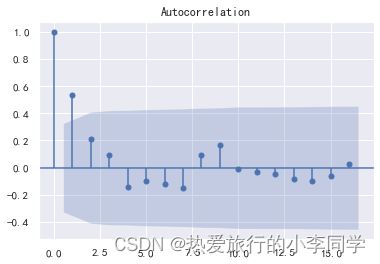
# 自相关图
plot_acf(d_data)
plt.show()

# 平稳性检验
print('差分序列的ADF检验结果为:\n', ADF(d_data))

差分序列的ADF检验结果为:
 (-3.1560562366723537, 0.022673435440048798, 0, 35, {'1%': -3.6327426647230316, '5%': -2.9485102040816327, '10%': -2.6130173469387756}, 287.5909090780334)

一阶差分后时序图在均值附近平稳波动，自相关图有较强的短期相关性，P值小于0.05，所以一阶差分后的序列是平稳序列
差分序列白噪声检验

# 白噪声检验
print('差分序列的白噪声检验结果为:\n', acorr_ljungbox(d_data, lags=1))

p值小于0.05，说明是平稳且非白噪声序列

差分序列的白噪声检验结果为:
 (array([11.30402222]), array([0.00077339]))

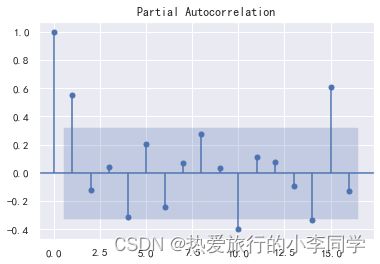
差分序列偏自相关系数PACF

# 偏自相关系数 pacf
plot_pacf(d_data)
plt.show()

4 构建ARIMA模型

ARIMA模型

ARIMA模型（英语：Autoregressive Integrated Moving Average model），差分整合移动平均自回归模型，又称整合移动平均自回归模型（移动也可称作滑动），是时间序列预测分析方法之一。ARIMA(p，d，q)中，AR是“自回归”，p为自回归项数；MA为“滑动平均”，q为滑动平均项数，d为使之成为平稳序列所做的差分次数（阶数）。“差分”一词虽未出现在ARIMA的英文名称中，却是关键步骤。

定阶

# 定阶
df['销量'] = df['销量'].astype(float)  # 转换为float类型
pmax = int(len(d_data) / 10)
qmax = int(len(d_data) / 10)
bic_matrix = []  # bic矩阵
for p in range(pmax + 1):
    tmp = []
    for q in range(qmax + 1):
        try:
            tmp.append(ARIMA(df, (p, 1, q)).fit().bic)
        except:
            tmp.append(None)
    bic_matrix.append(tmp)

bic_matrix = pd.DataFrame(bic_matrix)

bic_matrix

p, q = bic_matrix.stack().idxmin()
print('BIC最小的p值和q值为:%s. %s' % (p, q))

p, q = bic_matrix.stack().idxmin()
print('BIC最小的p值和q值为:%s. %s' % (p, q))

BIC最小的p值和q值为:0. 1

建立模型

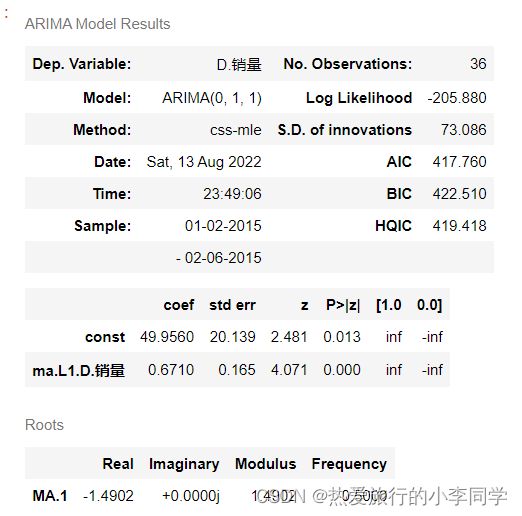
# 建立模型
model = ARIMA(df, (p, 1, q)).fit()
model.summary(2)  # 绘制一份模型报告

5 预测

# 预测5天，返回预测结果、标准误差、置信区间
model.forecast(5)

返回预测结果、标准误差、置信区间

(array([4873.96648392, 4923.92248997, 4973.87849602, 5023.83450207,
        5073.79050812]),
 array([ 73.08574325, 142.3267917 , 187.54280953, 223.80280422,
        254.95702569]),
 array([[4730.72105936, 5017.21190847],
        [4644.96710419, 5202.87787574],
        [4606.30134378, 5341.45564826],
        [4585.18906616, 5462.47993798],
        [4574.08392017, 5573.49709607]]))

6 踩坑日志

初次运行时，报错

TypeError: reduction operation 'argmin' not allowed for this dtype

查看bic矩阵，发现全是None

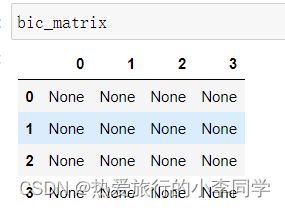
百度发现，原因时statsmodels版本更新了，之前的模板代码不能使用，只好降级到0.11.1，并使用清华源加速

pip install statsmodels==0.11.1 -i https://pypi.tuna.tsinghua.edu.cn/simple

后续，定阶计算p、q时，报错

C:\Users\leejack\.conda\envs\pytorch\lib\site-packages\statsmodels\tsa\base\tsa_model.py:159: ValueWarning: No frequency information was provided, so inferred frequency D will be used.

原因未知