MMoE论文中Synthetic Data生成代码(控制多任务学习中任务之间的相关性)
Synthetic Data
-
- 一. 前言
- 二. 程序实现
-
- 2.1 生成一条数据
- 2.2 生成一组相关系数为p的数据集
- 2.3 权重系数的余弦相似度与标签相关系数之间的关系
一. 前言
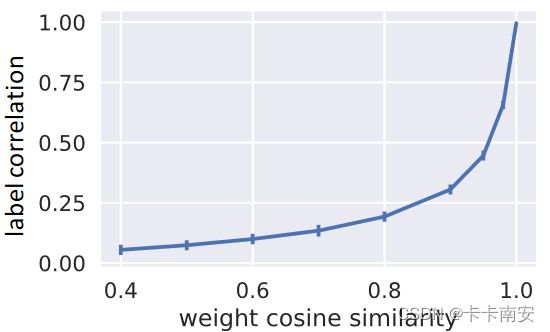
在MMoE论文中，作者人工生成了可以控制不同任务之间相关系数的数据集，并观察不同模型在不同相关系数的多任务学习中的模型效果，如下所示：
文中作者给出了数据集生成的数学表达：
下面用程序实现以上过程。
二. 程序实现
from scipy.linalg import *
import numpy as np
from tqdm import *
import matplotlib.pyplot as plt
2.1 生成一条数据
1.生成正交单位向量
d = 512 #维度
'''随机生成两个单位向量'''
np.random.seed(10)
u1 = np.random.randn(d)
u1 = u1 / np.linalg.norm(u1)
np.random.seed(22)
u2 = np.random.randn(d)
u2 = u2 / np.linalg.norm(u2)
u = np.vstack((u1,u2)).T #(d,2)
'''向量正交化'''
o = orth(u)
u1 = o[:,0]
u2 = o[:,1]
print(np.linalg.norm(u1))
print(np.linalg.norm(u2))
print(np.matmul(u1.T,u2))
'u1,u2为一组正交单位向量'
输出：
1.0000000000000002
1.0000000000000002
1.97758476261356e-16
2.生成权重向量
c = 1 #常数
p = 0.5 #相关系数 [-1,1]
w1 = c*u1
w2 = c*(p*u1 + np.sqrt(1-p*p)*u2)
3.随机生成自变量x
np.random.seed(2022)
x = np.random.randn(d)
4. 随机生成m组正弦函数参数
m = 10 #组合正弦的数量
'''随机生成生成m组正弦函数参数'''
np.random.seed(42)
ab = np.random.randn(2,m)
a = ab[0,:] #(m,)
b = ab[1,:] #(m,)
5. 生成数据标签
y1 = np.matmul(w1.T,x)
y2 = np.matmul(w2.T,x)
for i in range(m):
y1 = y1+np.sin(a[i]*np.matmul(w1.T,x)+b[i])
y2 = y2+np.sin(a[i]*np.matmul(w2.T,x)+b[i])
y1 += np.random.normal(0,0.01,1)
y2 += np.random.normal(0,0.01,1)
y = np.hstack((y1,y2))
这样我们就得到了相关系数为p的一条数据，其中 x 的长度为d，y 的长度为2。
接下来将上面的步骤整理一下生成一组完整的相关系数为p的数据集。
2.2 生成一组相关系数为p的数据集
1.生成正交单位向量
d = 512 #维度
'''生成两个单位向量'''
np.random.seed(10)
u1 = np.random.randn(d)
u1 = u1 / np.linalg.norm(u1)
np.random.seed(22)
u2 = np.random.randn(d)
u2 = u2 / np.linalg.norm(u2)
u = np.vstack((u1,u2)).T #(d,2)
'''向量正交化'''
o = orth(u)
u1 = o[:,0]
u2 = o[:,1]
print(np.linalg.norm(u1))
print(np.linalg.norm(u2))
print(np.matmul(u1.T,u2))
'u1,u2为一组正交单位向量'
2.生成权重系数矩阵
c = 1 #常数
p = 0.5 #相关系数 [-1,1]
w1 = c*u1
w2 = c*(p*u1 + np.sqrt(1-p*p)*u2)
3. 随机生成m组正弦函数参数
m = 10 #组合正弦的数量
np.random.seed(42)
ab = np.random.randn(2,m)
a = ab[0,:] #(m,)
b = ab[1,:] #(m,)
4.生成长度为L的数据集
l = 5000
for i in tqdm(range(l)):
'随机生成自变量x'
np.random.seed(2000+i)
x = np.random.randn(d) #(d,)
'生成因变量y1和y2'
y1 = np.matmul(w1.T,x)
y2 = np.matmul(w2.T,x)
for j in range(m):
y1 = y1+np.sin(a[j]*np.matmul(w1.T,x)+b[j])
y2 = y2+np.sin(a[j]*np.matmul(w2.T,x)+b[j])
y1 += np.random.normal(0,0.01,1)
y2 += np.random.normal(0,0.01,1)
y = np.hstack((y1,y2)) #(1,2)
'保存生成的x和y'
if i==0:
X = x
Y = y
else:
X = np.vstack((X,x))
Y = np.vstack((Y,y))
print(X.shape)
print(Y.shape)
输出：
(5000, 512)
(5000, 2)
下面比较一下权重系数的余弦相似度和label之间的皮尔逊相关系数：
'计算w1和w2的余弦相似度'
cos_sim = w1.dot(w2) / (np.linalg.norm(w1)*np.linalg.norm(w2))
print("cos(w1,w2)=",cos_sim)
'计算label之间的皮尔逊相关系数'
corr = np.corrcoef(Y[:,0],Y[:,1])
print("person(y1,y2)=",corr[0,1])
输出：
cos(w1,w2)= 0.5000000000000002
person(y1,y2)= 0.39918604117923223
可以看到权重系数的余弦相似度与标签的皮尔逊相关系数并不完全相同，因为 y 是关于 x 的非线性函数，下面探究一下两者之间的关系。
2.3 权重系数的余弦相似度与标签相关系数之间的关系
在原文中，作者提到二者之间的关系如图所示：
1.生成正交单位向量
'1. 生成正交单位向量'
d = 512 #维度
'''生成两个单位向量'''
np.random.seed(10)
u1 = np.random.randn(d)
u1 = u1 / np.linalg.norm(u1)
np.random.seed(22)
u2 = np.random.randn(d)
u2 = u2 / np.linalg.norm(u2)
u = np.vstack((u1,u2)).T #(d,2)
'''向量正交化'''
o = orth(u)
u1 = o[:,0]
u2 = o[:,1]
print(np.linalg.norm(u1))
print(np.linalg.norm(u2))
print(np.matmul(u1.T,u2))
'u1,u2为一组正交单位向量'
2.随机生成生成m组正弦函数的参数
m = 10 #组合正弦的数量
np.random.seed(42)
ab = np.random.randn(2,m)
a = ab[0,:] #(m,)
b = ab[1,:] #(m,)
3.循环得到不同p时对应的权重和标签的相似度
c = 1 #常数
l = 5000 #数据长度
cs=[]
pc=[]
for p in np.arange(-1,1.1,0.1).round(1):
print("***** p={} *****".format(p))
w1 = c*u1
w2 = c*(p*u1 + np.sqrt(1-p*p)*u2)
for i in tqdm(range(l)):
'随机生成自变量x'
np.random.seed(2000+i)
x = np.random.randn(d) #(d,)
'生成因变量y1和y2'
y1 = np.matmul(w1.T,x)
y2 = np.matmul(w2.T,x)
for j in range(m):
y1 = y1+np.sin(a[j]*np.matmul(w1.T,x)+b[j])
y2 = y2+np.sin(a[j]*np.matmul(w2.T,x)+b[j])
y1 += np.random.normal(0,0.01,1)
y2 += np.random.normal(0,0.01,1)
y = np.hstack((y1,y2)) #(1,2)
'保存生成的x和y'
if i==0:
X = x
Y = y
else:
X = np.vstack((X,x))
Y = np.vstack((Y,y))
'计算w1和w2的余弦相似度'
cos_sim = w1.dot(w2) / (np.linalg.norm(w1)*np.linalg.norm(w2))
cs.append(cos_sim)
'计算label之间的皮尔逊相关系数'
person_corr = np.corrcoef(Y[:,0],Y[:,1])
pc.append(person_corr[0,1])
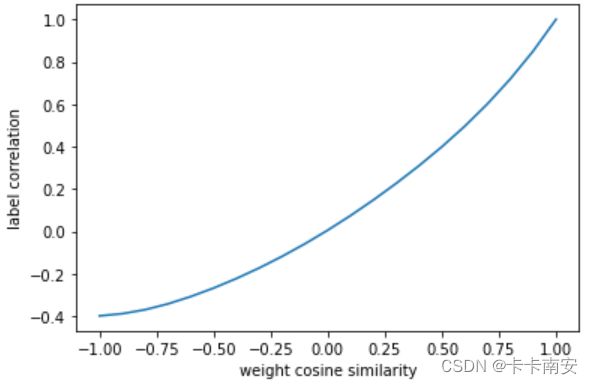
4.绘制图像
plt.plot(cs,pc,linewidth=1.5)
# 设置横轴标签
plt.xlabel('weight cosine similarity')
# 设置纵轴标签
plt.ylabel('label correlation')
plt.show()
可以看到二者确实不是线性关系，但是呈正相关，因此可以用设置的相关系数p表示任务之间的相关性。