《MATLAB智能算法30个案例》：第7章 多种群遗传算法的函数优化算法

1. 前言

《MATLAB智能算法30个案例分析》是2011年7月1日由北京航空航天大学出版社出版的图书，作者是郁磊、史峰、王辉、胡斐。本书案例是各位作者多年从事算法研究的经验总结。书中所有案例均因国内各大MATLAB技术论坛网友的切身需求而精心设计，其中不少案例所涉及的内容和求解方法在国内现已出版的MATLAB书籍中鲜有介绍。《MATLAB智能算法30个案例分析》采用案例形式，以智能算法为主线，讲解了遗传算法、免疫算法、退火算法、粒子群算法、鱼群算法、蚁群算法和神经网络算法等最常用的智能算法的MATLAB实现。

本书共给出30个案例，每个案例都是一个使用智能算法解决问题的具体实例，所有案例均由理论讲解、案例背景、MATLAB程序实现和扩展阅读四个部分组成，并配有完整的原创程序，使读者在掌握算法的同时更能快速提高使用算法求解实际问题的能力。《MATLAB智能算法30个案例分析》可作为本科毕业设计、研究生项目设计、博士低年级课题设计参考书籍，同时对广大科研人员也有很高的参考价值。

《MATLAB智能算法30个案例分析》与《MATLAB 神经网络43个案例分析》一样，都是由北京航空航天大学出版社出版，其中的智能算法应该是属于神经网络兴起之前的智能预测分类算法的热门领域，在数字信号处理，如图像和语音相关方面应用较为广泛。本系列文章结合MATLAB与实际案例进行仿真复现，有不少自己在研究生期间与工作后的学习中有过相关学习应用，这次复现仿真示例进行学习，希望可以温故知新，加强并提升自己在智能算法方面的理解与实践。下面开始进行仿真示例，主要以介绍各章节中源码应用示例为主，本文主要基于MATLAB2015b(32位)平台仿真实现，这是本书第七章多种群遗传算法的函数优化算法实例，话不多说，开始！

2. MATLAB 仿真示例

打开MATLAB，点击“主页”，点击“打开”，找到示例文件

选中MPGA.m，点击“打开”

MPGA.m源码如下：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%功能：多种群遗传算法示例
%环境：Win7，Matlab2015b
%Modi: C.S
%时间：2022-07-5
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%% 清空环境
clc
clear all
close all

tic
NIND=40;               %个体数目
NVAR=2;                %变量的维数
PRECI=20;              %变量的二进制位数
GGAP=0.9;              %代沟
MP=10;                 %种群数目
FieldD=[rep(PRECI,[1,NVAR]);[-3,4.1;12.1,5.8];rep([1;0;1;1],[1,NVAR])];  %译码矩阵
for i=1:MP
    Chrom{i}=crtbp(NIND, NVAR*PRECI);                       %创建初始种群
end
pc=0.7+(0.9-0.7)*rand(MP,1);    %在【0.7,0.9】范围i内随机产生交叉概率
pm=0.001+(0.05-0.001)*rand(MP,1);  %在【0.001,0.05】范围内随机产生变异概率
gen=0;  %初始遗传代数
gen0=0; %初始保持代数
MAXGEN=10;  %最优个体最少保持代数
maxY=0; %最优值
for i=1:MP
    ObjV{i}=ObjectFunction(bs2rv(Chrom{i}, FieldD));%计算各初始种群个体的目标函数值
end
MaxObjV=zeros(MP,1);           %记录精华种群
MaxChrom=zeros(MP,PRECI*NVAR); %记录精华种群的编码
while gen0<=MAXGEN
    gen=gen+1;       %遗传代数加1
    for i=1:MP
        FitnV{i}=ranking(-ObjV{i});                      % 各种群的适应度
        SelCh{i}=select('sus', Chrom{i}, FitnV{i},GGAP); % 选择操作
        SelCh{i}=recombin('xovsp',SelCh{i}, pc(i));      % 交叉操作
        SelCh{i}=mut(SelCh{i},pm(i));                    % 变异操作
        ObjVSel=ObjectFunction(bs2rv(SelCh{i}, FieldD)); % 计算子代目标函数值
        [Chrom{i},ObjV{i}]=reins(Chrom{i},SelCh{i},1,1,ObjV{i},ObjVSel);    %重插入操作
    end
    [Chrom,ObjV]=immigrant(Chrom,ObjV);     % 移民操作
    [MaxObjV,MaxChrom]=EliteInduvidual(Chrom,ObjV,MaxObjV,MaxChrom);     % 人工选择精华种群
    YY(gen)=max(MaxObjV);    %找出精华种群中最优的个体
    if YY(gen)>maxY   %判断当前优化值是否与前一次优化值相同
        maxY=YY(gen); %更新最优值
        gen0=0;
    else
        gen0=gen0+1; %最优值保持次数加1
    end
end
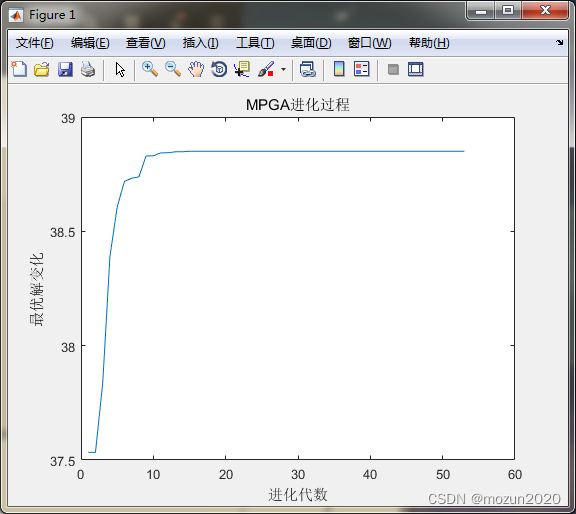
%% 进化过程图
plot(1:gen,YY);
xlabel('进化代数')
ylabel('最优解变化')
title('MPGA进化过程')

%% 输出最优解
[Y,I]=max(MaxObjV);    %找出精华种群中最优的个体
X=(bs2rv(MaxChrom(I,:), FieldD));   %最优个体的解码解
disp(['最优值为：',num2str(Y)])
disp(['对应的自变量取值：',num2str(X)])
toc

添加完毕，点击“运行”，开始仿真，输出仿真结果如下：

最优值为：38.8503
对应的自变量取值：11.6255      5.72504

3. 小结

传统的遗传算法是一种借鉴于生物界自然选择和进化机制发展起来的高度并行、随机、自适应的全局优化概率搜索算法。因为优化时不依赖于梯度，具有很强的鲁棒性和全局搜索能力。但是未成熟收敛确实遗传算法中不可忽视的现象，它主要表现为所有个体都区域同一状态而停止进化。

多种群遗传算法正是为解决该问题而提出，它主要引入以下三个概念：

1. 突破SGA仅靠单个种群进行遗传进化的框架，引入多个种群进行全局搜索，不同种群用不同参数，实现不同的搜索目的。
2. 各种群之间通过移民算子进行联系，实现了多种群协同进化，最优解是多个种群共同进化的结果。
3. 通过人工算子保留每代中的最优个体，并作为判断收敛的依据。

对本章内容感兴趣或者想充分学习了解的，建议去研习书中第七章节的内容。后期会对其中一些知识点在自己理解的基础上进行补充，欢迎大家一起学习交流。