PyTorch深度学习实践概论笔记11练习1-ResNet论文阅读

在PyTorch深度学习实践概论笔记11-卷积神经网络高级篇中介绍了GoogLeNet（包括Inception Module）以及Residual Block，为进一步学习ResNet网络，需要阅读论文。

论文链接：https://arxiv.org/pdf/1512.03385.pdf

1.Introduction

在第一部分Introduction中，作者阐述了在图像分类（image classification）领域深度卷积神经网络的研究成果。[41,44]表明“最近的证据表明网络深度至关重要”。

既然深度很重要，那么学习更好的网络就像叠加更多的层一样容易吗?答案是否定的。容易出现两个问题：

• 梯度消失或梯度下降问题（vanishing/exploding gradients）。这个问题已经在很大程度上通过标准初始化[23,9,37,13]和标准化中间层得到了解决。
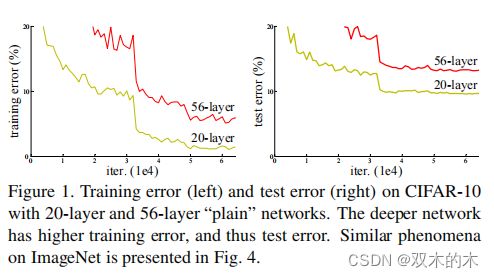
• 退化问题（degradation problem）。作者的实验结果看下图Fig1，而且这种退化不是由过拟合（overfitting）引起的。论文提出了一种构建更深层模型的解决方法：添加的层是恒等映射（identity mapping）。

如上图是在CIFAR-10上使用20层和56层“普通”网络的训练错误(左)和测试错误(右)。网络越深，训练误差越大，测试误差也越大。在ImageNet上有类似的现象，如下图Fig4所示。

由此看到在构建更深的模型时，直接堆叠layers容易造成退化问题。

在论文中，作者介绍了一个深度残差学习框架（deep residual learning framework）来解决退化问题。作者不希望每几个堆叠的层都直接拟合所需的基础映射（underlying mapping），而是直接让这些层拟合残差映射（residual mapping）。一般记：

• H(x)为所需的基础映射（underlying mapping）
• F(x):=H(x)-x为堆叠的非线性层拟合的另一个映射
• F(x)+x为原始映射（original mapping）

论文假设残差映射比原始的、未参考的映射更容易优化。在极端情况下，如果一个恒等映射是最优的（optimize），那么将残差置为零比通过一堆非线性层来拟合恒等映射更容易。

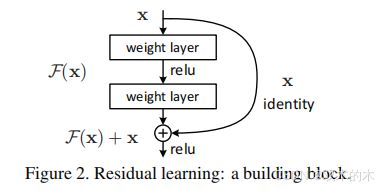
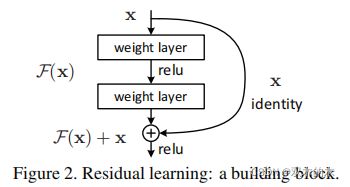
公式F(x)+x可以通过带有“捷径连接”（shortcut connections）的前向神经网络（Fig2）来实现。在本论文的案例中，捷径连接简单地执行恒等映射（identity mapping），并将其输出添加到堆叠层的输出（Fig2）。

恒等捷径连接既不增加额外的参数也不增加计算复杂度。整个网络仍然可以由带有反向传播的SGD进行端到端（end to end）的训练，并且可以使用公共库（如Caffe）轻松实现，而无需修改求解器。

接着论文在ImageNet和CIFAR-10数据集上实验了残差网络。

在ImageNet[35]上实验发现：1）当深度增加时极深的残差网络易于优化，对应的“简单”网络（简单堆叠层）表现出更高的训练误差；2）深度残差网络可以从大大增加的深度中轻松获得准确性收益，生成的结果实质上比以前的网络更好。

CIFAR-10[20]也显示出类似的现象，这表明了优化的困难以及论文的方法的影响不仅仅是针对一个特定的数据集。在CIFAR-10上成功训练的超过100层的模型，并探索了超过1000层的模型。

总的来说，在ImageNet分类数据集[35]中，论文通过非常深的残差网络获得了很好的结果（excellent results）。152层残差网络是ImageNet上最深的网络，同时还具有比VGG网络[40]更低的复杂性。在ImageNet测试集上有3.57% top-5的错误率，并在ILSVRC 2015分类比赛中获得了第一名。在其它识别任务中也有极好的泛化性能，赢得了第一名：包括ILSVRC & COCO 2015竞赛中的ImageNet检测，ImageNet定位，COCO检测和COCO分割。有力的证据表明残差学习准则是通用的（generic），并且作者期望它适用于其它的视觉和非视觉问题。

2. Related Work

残差表示（Residual Representations）

在图像识别中，VLAD[18]是一种通过关于字典的残差向量（residual vectors）进行编码的表示形式，Fisher矢量[30]是VLAD的概率版本[18]。它们都是图像检索和图像分类[4,47]中强大的浅层表示（shallow representations）。对于矢量量化，编码残差向量[17]被证明比编码原始向量更有效。

在低级视觉和计算机图形学中，为了求解偏微分方程（PDE），广泛使用的Multigrid方法[3]将系统重构为在多个尺度上的子问题，其中每个子问题负责较粗尺度和较细尺度的残差解（residual solution）。Multigrid的替代方法是层次化基础预处理[44,45]，它依赖于表示两个尺度之间残差向量的变量。已经被证明[3,44,45]这些求解器比不知道解的残差性质的标准求解器收敛得更快。这些方法表明，良好的重构或预处理可以简化优化。

捷径连接（Shortcut Connections）

导致捷径连接[2,33,48]的实践和理论已经被研究了很长时间。训练多层感知机（MLPs）的早期实践是添加一个线性层来连接网络的输入和输出[33,48]。在[43,24]中一些中间层直接连接到辅助分类器，用于解决梯度消失/爆炸。论文[38,37,31,46]提出了通过快捷连接实现层间响应，梯度和传播误差的方法。在[43]中，一个“inception”层由一个快捷分支和一些更深的分支组成。

与论文工作的同一时刻，“highway networks” [41, 42]提出了门功能（gating functions）的捷径连接。这些门是数据相关且有参数的，与我们不具有参数的恒等捷径连接相反。当门控捷径连接“关闭”（接近零）时，“highway networks”中的层表示非残差函数。相反，论文的公式总是学习残差函数；恒等捷径连接永远不会关闭，所有的信息总是通过，还有额外的残差函数要学习。此外，“highway networks”还没有证实极度增加的深度（例如，超过100个层）带来的准确性收益。

3. Deep Residual Learning

3.1. Residual Learning

论文将H(x)作为几个堆叠层（不必是整个网络）要拟合的基础映射（underlying mapping），x表示这些层中第一层的输入。假设多个非线性层可以渐近近似复杂函数（asymptotically approximate complicated functions），论文等价于假设它们可以渐近近似残差函数，即H(x)-x(假设输入输出是相同维度)【这里的多个非线性层近似的参数函数F(x)，我理解的是拟合模型的卷积层部分，就是基础映射H(x)中去掉恒等映射x的部分】。因此，论文明确让这些层近似参数函数F(x):=H(x)-x，而不是期望堆叠层近似H(x)。因此原始函数（original function）变为F(x)+x。尽管两种形式应该都能渐近近似要求的函数（如假设），但学习的难易程度可能是不同的。

关于退化问题的反直觉现象激发了这种重构（reformulation）【指论文的残差结构】（图1左）。在引言中，如果添加的层可以被构建为恒等映射，更深模型的训练误差应该不大于它对应的更浅版本【个人理解：相当于添加的层的不做任何处理，只执行f(x)=x，更深层的模型也就等价于浅层模型，深层网络效果也不应该比更浅层的差】。退化问题表明求解器（solvers）通过多个非线性层来近似恒等映射可能有困难。通过残差学习的重构，如果恒等映射是最优的，求解器可能简单地将多个非线性连接的权重推向零来接近恒等映射。

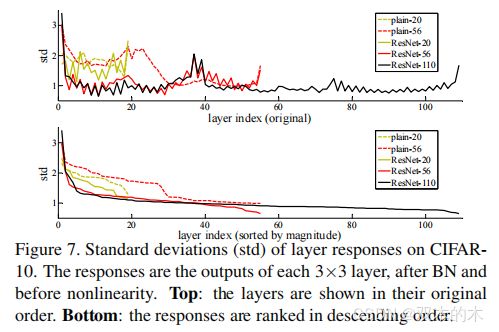
在实际情况下，恒等映射不太可能是最优的，但是我们的重构可能有助于对问题进行预处理（precondition the problem）。如果最优函数比零映射更接近于恒等映射，则求解器应该更容易找到关于恒等映射的扰动（perturbations），而不是将该函数作为新函数来学习。论文通过实验（Fig7）显示学习的残差函数通常有更小的响应，表明恒等映射提供了合理的预处理。

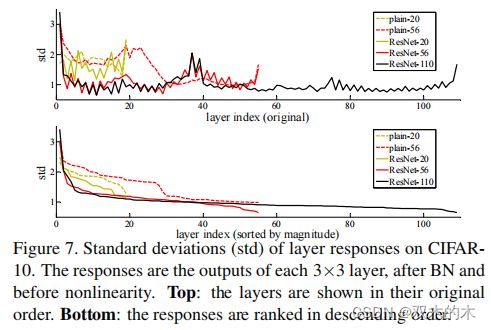
图7。层响应在CIFAR-10上的标准差（std）。这些响应是每个3×3层的输出，在BN之后非线性之前。上图：以原始顺序显示层。下图：响应按降序排列。

3.2.Identity Mapping by Shortcuts

我们每隔几个堆叠层采用残差学习。构建块如Fig2所示。在本文中我们考虑构建块正式定义为：

其中x和y是所考虑层的输入和输出向量。函数表示要学习的残差映射。Fig2中的例子有两层，中σ表示ReLU[29]，为了简化写法忽略偏置项。通过捷径连接（shortcut connection）和各个元素相加（element-wise addition）来执行。在相加之后论文采纳了第二种非线性（即σ(y)，看Fig2）。

方程(1)中的捷径连接既没有引入外部参数又没有增加计算复杂度。这不仅在实践中有吸引力，而且在简单网络（plain）和残差网络（residual network）的比较中也很重要。论文可以公平地比较同时具有相同数量的参数，相同深度，宽度和计算成本的简单/残差网络（除了不可忽略的元素加法之外）。

方程(1)中x和F的维度必须是相等的。如果不是这种情况（例如，当更改输入/输出通道时），论文可以通过捷径连接执行线性投影（linear projection）来匹配维度：

也可以使用方程(1)中的方阵。但是实验表明，恒等映射足以解决退化问题，并且是节约的（economical），因此仅在匹配维度时使用。

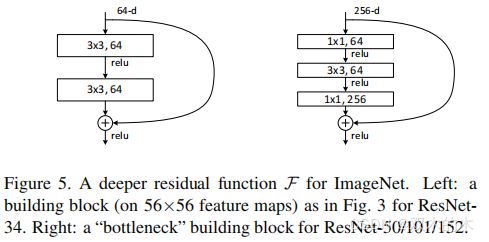
残差函数F的形式是可变的。论文中的实验包括有两层或三层（Fig5）的函数，同时可能有更多的层。但如果F只有一层，方程(1)类似于线性层：，我们没有看到优势。【解释了残差块为什么不使用一层的结构】

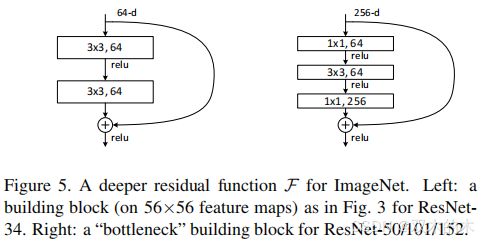
Fig5。ImageNet的深度残差函数F。左：ResNet-34的构建块（在56×56的特征图上），如Fig3。右：ResNet-50/101/152的“bottleneck”构建块。

论文提到，尽管上述符号是关于全连接层的，但它们同样适用于卷积层。函数可以表示多个卷积层。元素加法是在两个特性图上进行的，一个通道接一个通道（channel by channel）。

3.3. Network Architectures

论文测试了各种简单/残差网络，并观察到了一致的现象，主要描述了ImageNet的两个模型。

简单网络（Plain Network）

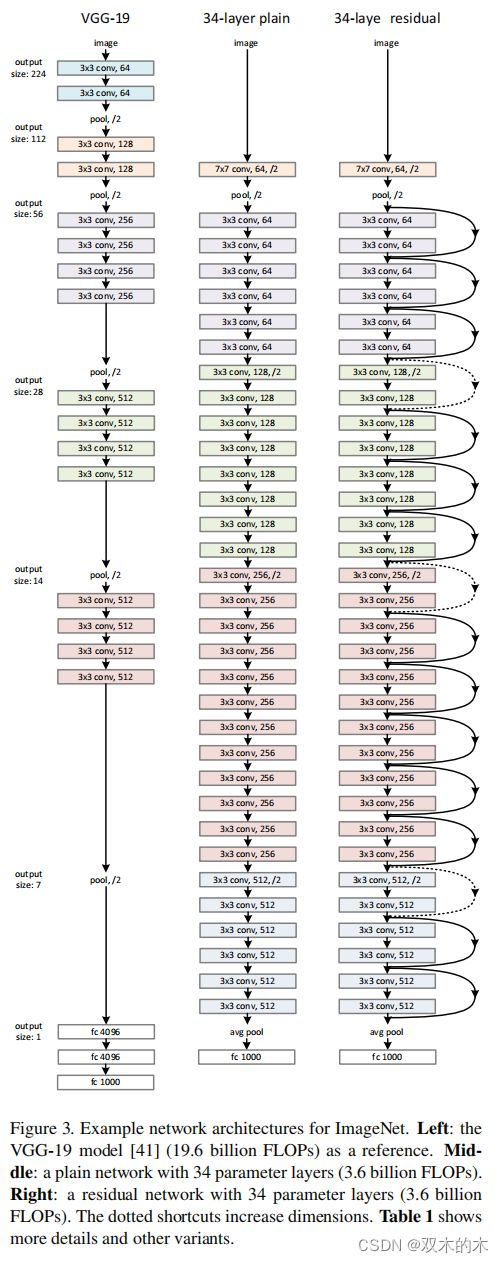
简单网络的基准主要受到VGG网络[40]的哲学启发。卷积层主要有3×3的滤波器（filters），并遵循两个简单的设计规则：（i）对于相同的输出特征图尺寸的层具有相同数量的滤波器；（ii）如果特征图尺寸减半，则滤波器数量加倍，来保持每层的时间复杂度（time complexity）。通过步长为2的卷积层直接执行下采样（downsampling）。网络以全局平均池化层和具有softmax的1000维全连接层结束。图如Fig3中间所示，加权层总数为34。

Fig3。ImageNet的网络架构例子。左：作为参考的VGG-19模型。中：具有34个参数层的简单网络（36亿FLOPs）。右：具有34个参数层的残差网络（36亿FLOPs）。带点的快捷连接增加了维度。表1显示了更多细节和其它变种。

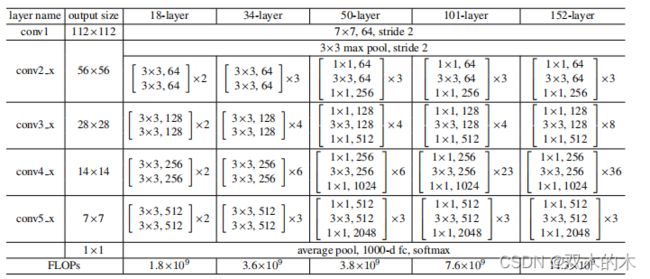
表1（构建网络的关键表）。ImageNet架构。构建块（building blocks）显示在括号中（也可看Fig5），以及构建块的堆叠数量。步长为2的下采样通过conv3_1, conv4_1和conv5_1执行。

值得注意的是论文提出的模型与VGG网络（Fig3左）相比，有更少的滤波器和更低的复杂度（fewer fifilters and lower complexity）。34层基准有36亿FLOPs(乘加)，仅是VGG-19（196亿FLOPs）的18%。

残差网络（Residual Network）

基于上述的简单网络，论文插入捷径连接（shortcut connections）（Fig3，右），将网络转换为其对应的残差版本。

• 当输入和输出具有相同的维度时（图3中的实线捷径连接）时，可以直接使用恒等捷径连接（方程(1)）。
• 当维度增加（图3中的虚线捷径连接）时，论文考虑两个选项【后面会用到】：
  • （A）捷径连接仍然执行恒等映射，额外填充零输入以增加维度，此选项不会引入额外的参数；
  • （B）方程(2)中的投影捷径连接用于匹配维度（由1×1卷积完成）。对于这两个选项，当捷径连接跨越两种尺寸的特征图时，它们执行时步长为2。

3.4. Implementation

ImageNet中论文的实现遵循[21，40]的实践。

• 调整图像大小，其较短的边在[256,480]之间进行随机采样，用于尺度增强（scale augmentation）[40]
• 224×224裁剪是从图像或其水平翻转中随机采样，并逐像素减去均值[21]
• 使用了[21]中的标准颜色增强（standard color augmentation）
• 在每个卷积之后和激活之前，我们采用批量归一化（BN）[16]
• 论文按照[12]的方法初始化权重（initialize the weights），从零开始训练所有的简单/残差网络
• 使用批大小为256的SGD方法
• 学习速度（learning rate）从0.1开始，当误差稳定时学习率除以10
• 训练高达60 × 10e4次迭代（iterations）
• 权重衰减（weight decay）为0.0001，
• 动量（momentum）为0.9
• 根据[16]的实践，不使用dropout[13]

在测试阶段，采用标准的10-crop测试[21]进行比较学习。对于最好的结果，采用如[40, 12]中的全卷积形式（fully-convolutional form），并在多尺度上对分数进行平均（图像resize，短边位于{224, 256, 384, 480, 640}中）。

4. Experiments

4.1. ImageNet Classifification

论文在ImageNet 2012分类数据集[35]进行了评估，该数据集由1000个类别组成。这些模型在128万张训练图像（training images）上进行训练，并在5万张验证图像（validation images）上进行评估，同时也获得了测试服务器报告的在10万张测试图像上的最终结果。论文评估了top-1和top-5错误率。

简单网络（Plain Networks）

首先评估18层和34层的简单网络。34层简单网络在Fig3（中间）。18层简单网络是一种类似的形式。详细体系结构请看表1。

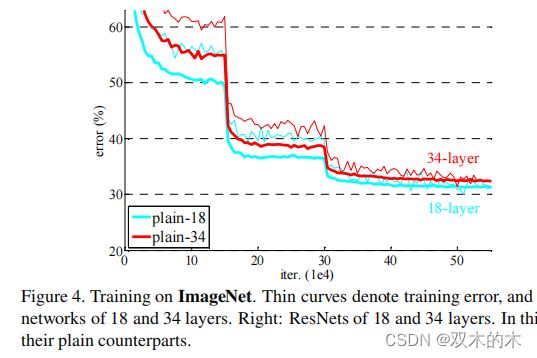
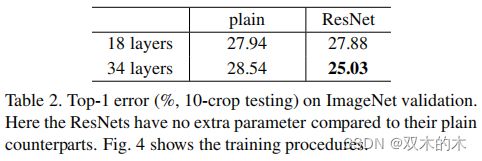
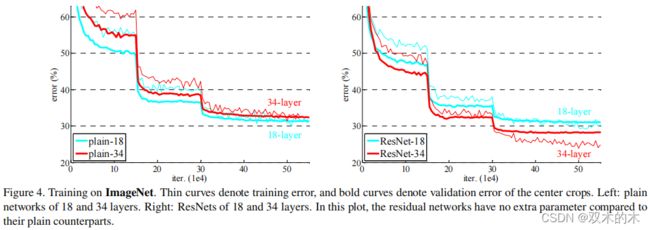
表2中的结果表明，较深的34层简单网络比较浅的18层简单网络有更高的验证误差（higher validation error）。为了揭示原因，在Fig4（左图）中，我们比较训练过程中的训练/验证误差。我们观察到退化问题——虽然18层简单网络的解空间是34层简单网络解空间的子空间，但34层简单网络在整个训练过程中具有较高的训练误差。

表2。ImageNet验证集上的Top-1错误率(%，10个裁剪图像测试)。相比于对应的简单网络，ResNet没有额外的参数。图4显示了训练过程（training procedures）。

Fig4。在ImageNet上训练。细曲线表示训练误差（training error），粗曲线表示中心裁剪图像的验证误差（validation error）。左：18层和34层的简单网络。右：18层和34层的ResNet。在本图中，残差网络与对应的简单网络相比没有额外的参数。

论文认为这种优化难度不可能是由于梯度消失（vanishing gradients）引起的。这些简单网络使用BN[16]训练，这保证了前向传播信号有非零方差。论文还验证了反向传播的梯度，结果显示其符合BN的正常标准。因此既不是前向信号消失也不是反向信号消失。实际上，34层简单网络仍能取得有竞争力的准确率（表3），这表明求解器仍工作。论文推测深度简单网络可能有指数级低收敛特性，这影响了训练误差的降低。这种优化困难的原因将来会研究。

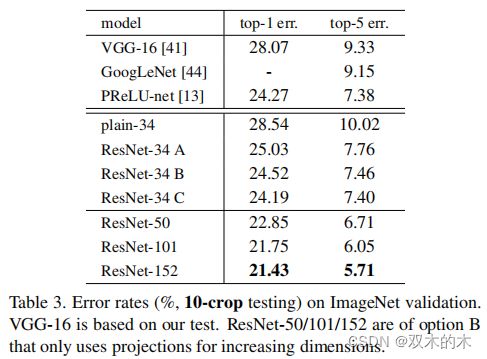
表3。ImageNet验证集错误率（%，10个裁剪图像测试）。VGG16是基于论文实验测试结果的。ResNet-50/101/152的选择B仅使用投影增加维度。

残差网络（Residual Networks）

接下来评估18层和34层残差网络（ResNets）。基准架构与简单网络相同，如图3（右）所示，预计每对3×3滤波器都会添加捷径连接。在第一次比较（表2和图4右侧）中，对所有捷径连接都使用恒等映射和零填充以增加维度（选项A）。与对应的简单网络相比，它们没有额外的参数。

从表2和图4中可以看到三个主要的观察结果。

• 首先，残留学习的情况变了——34层ResNet比18层ResNet更好（2.8％）。34层ResNet显示出较低的训练误差，并且可以泛化到验证数据。这表明退化问题此时得到了很好的解决，从增加的深度中设法获得了准确性收益（accuracy gains）。
• 第二，与对应的简单网络相比，由于成功的减少了训练误差，34层ResNet降低了3.5%的top-1错误率。这种比较证实了在极深系统中残差学习的有效性（effectiveness）。
• 最后，18层的简单/残差网络同样地准确（表2），但18层ResNet收敛更快（图4右和左）。当网络“不过度深”时（18层），目前的SGD求解器仍能在简单网络中找到好的解。在这种情况下，ResNet通过在早期提供更快的收敛进而简便了优化。

恒等和投影快捷连接（Identity vs. Projection Shortcuts）

论文表明没有增加参数（parameter-free），恒等捷径连接有助于训练。接下来研究投影捷径连接（方程2）。在表3中我们比较了三个选项：

• (A)零填充捷径连接用来增加维度，所有的捷径连接是没有参数的（与表2和图4右相同）
• (B)投影捷径连接用来增加维度，其它的捷径连接是恒等的
• (C)所有的捷径连接都是投影

表3显示，所有三个选项都比对应的简单网络好很多。选项B比A略好。这是因为A中的零填充确实没有残差学习。选项C比B稍好，由于许多（十三）投影快捷连接引入了额外参数。但A/B/C之间的细微差异表明，投影捷径连接对于解决退化问题不是至关重要的（not essential）。于是在本文的剩余部分不再使用选项C，以减少内存/时间复杂性和模型大小。恒等捷径连接对于不增加下面介绍的瓶颈结构的复杂性尤为重要（particularly important）。

更深的瓶颈结构（Deeper Bottleneck Architectures）

接下来在ImageNet中使用更深的网络。由于训练时间，论文将构建块（building block）修改为瓶颈设计（bottleneck design）。

对于每个残差函数F，使用3层堆叠而不是2层（图5）。三层是1×1，3×3和1×1卷积，其中1×1层负责减小然后增加（恢复）维度，使3×3层成为具有较小输入/输出维度的瓶颈。两个设计具有相似的时间复杂度。

无参数恒等捷径连接对于瓶颈架构尤为重要。如果图5（右）中的恒等捷径连接被投影替换，则可以显示出时间复杂度和模型大小加倍（doubled），因为捷径连接是连接到两个高维端。因此，恒等捷径连接可以为瓶颈设计得到更有效的模型。

50层ResNet：用3层瓶颈块替换34层网络中的每一个2层块，得到了一个50层ResNet（表1）。使用选项B来增加维度。该模型有38亿FLOP。

101层和152层ResNet：通过使用更多的3层瓶颈块来构建101层和152层ResNets（表1）。尽管深度显著增加，但152层ResNet（113亿FLOPs）仍然比VGG-16/19网络（153/196亿FLOPs）具有更低的复杂度。

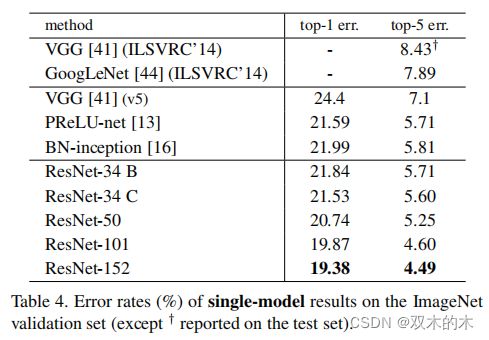
50/101/152层ResNet比34层ResNet的准确性要高得多（表3和4）。论文没有观察到退化问题，因此可以从显著增加的深度中获得显著的准确性收益。所有评估指标都能证明深度带来的收益（表3和表4）。

与最先进的方法比较（Comparisons with State-of-the-art Methods）

在表4中，与以前最好的单一模型结果进行比较。

表4。单一模型在ImageNet验证集上的错误率（%）(除了†是测试集上报告的错误率)。

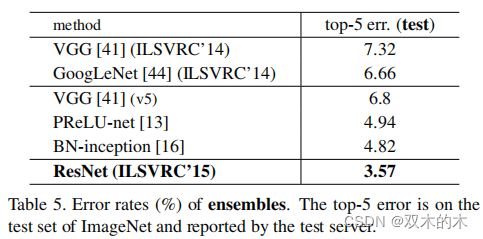
基准的34层ResNet取得了非常有竞争力的准确性。152层ResNet具有单模型4.49％的top-5错误率。这种单一模型的结果胜过之前所有综合的结果（表5）。论文结合了六种不同深度的模型，形成一个集合（在提交时仅有两个152层）。在测试集上得到了3.5％的top-5错误率（表5）。这次提交在2015年ILSVRC中荣获了第一名。

表5。模型综合的错误率(%)。top-5错误率是ImageNet测试集上的并由测试服务器报告的。

4.2. CIFAR-10 and Analysis

论文对CIFAR-10数据集[20]进行了更多的研究，其中包括10个类别中的5万张训练图像和1万张测试图像。实验的焦点在于极深网络的行为，但不是推动最先进的结果，所以使用如下的简单架构。

简单/残差架构遵循图3（中/右）的形式：

• 网络输入是32×32的图像，每个像素减去均值
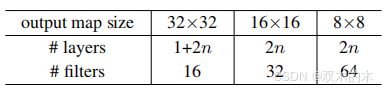
• 第一层是3×3卷积，然后在大小为{32,16,8}的特征图上分别使用了带有3×3卷积的6n个堆叠层，每个特征图大小使用2n层
• 滤波器数量分别为{16,32,64}
• 下采样由步长为2的卷积进行
• 网络以全局平均池化（global average pooling），一个10维全连接层和softmax作为结束

共有6n+2个堆叠的加权层。下表总结了这个架构：

当使用捷径连接时，它们连接到成对的3×3卷积层上（共3n个捷径连接）。在这个数据集上，在所有案例中都使用恒等捷径连接（即选项A），因此残差模型与对应的简单模型具有完全相同的深度，宽度和参数数量。

训练时的一些参数：

• 这里使用的权重衰减为0.0001和动量为0.9
• 采用权重初始化[13]和BN[16]但是没有dropout
• 模型在两个GPU上进行训练，批处理大小为128
• 开始的学习率为0.1，在32k次和48k次迭代后学习率除以10，并在64k次迭代后终止训练（由45k/5k的训练/验证集分割决定）
• 按照[24]中的简单数据增强进行训练：每边填充4个像素，并从填充图像或其水平翻转图像中随机采样32×32的裁剪图像

对于测试，只评估原始32×32图像的单一视图。

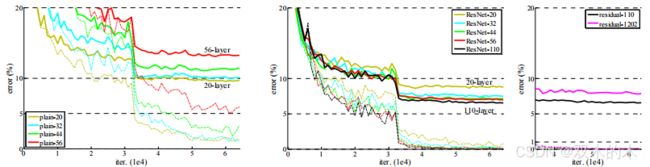
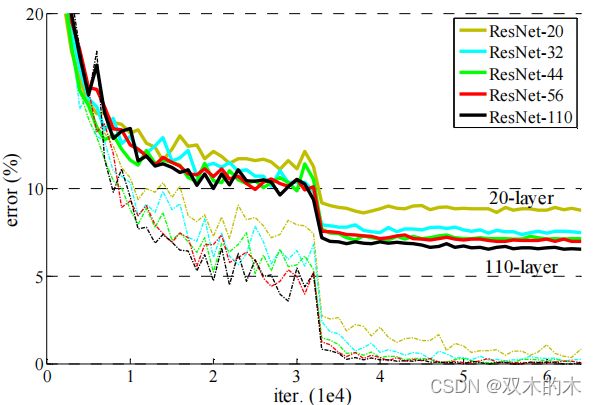
实验比较了n={3,5,7,9}，得到了20,32,44和56层的网络。图6（左）是简单网络的表现。深度简单网络随着深度增加表现出了更高的训练误差。这种现象类似于ImageNet中（图4，左）和MNIST中（请看[41]）的现象，表明这种优化困难是一个基本的问题。

Fig6。在CIFAR-10上训练。虚线表示训练误差，粗线表示测试误差。左：简单网络。简单的110层网络错误率超过60%没有展示。中间：ResNet。右：110层ResNet和1202层ResNet。

图6（中）显示了ResNet的行为。与ImageNet的情况类似，ResNet设法克服优化困难并随着深度的增加展示了准确性收益。

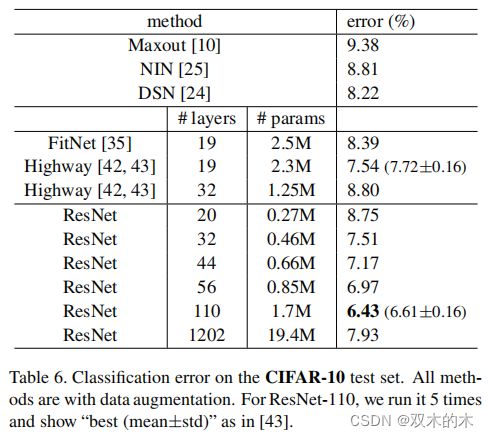
进一步探索110层ResNet（n=18）。在这种情况下，实验发现0.1的初始学习率对于收敛来说太大了。因此使用0.01的学习率开始训练，直到训练误差低于80%（大约400次迭代），学习率变回到0.1并继续训练。学习过程的剩余部分与前面做的一样。这个110层网络收敛的很好（图6，中）。它与其它的深且窄的网络例如FitNet[34]和Highway[42]相比有更少的参数，但结果仍在目前最好的结果之间（6.43%，表6）。

表6。在CIFAR-10测试集上的分类误差。所有的方法都用了数据增强。对于ResNet110，像论文[43]中那样，运行了5次并展示了“最好的(mean±std)”。

层响应分析（Analysis of Layer Responses）

图7显示了层响应的标准偏差（std）。

这些响应是每个3×3层的输出，在BN之后和其他非线性（ReLU/加法）之前。对于ResNets，该分析揭示了残差函数的响应强度。图7显示ResNet的响应比其对应的简单网络的响应更小。这些结果支持了论文的基本动机（basic motivation）（第3.1节），残差函数通常具有比非残差函数更接近零。同时更深的ResNet具有较小的响应幅度。当层数更多时，单层ResNet趋向于更少地修改信号。

探索超过1000层（Exploring Over 1000 layers）

论文探索超过1000层的模型，设置n=200，得到了1202层的网络，其训练如上所述。残差的方法显示没有优化困难，这个层网络能够实现训练误差<0.1％（图6，右图）。其测试误差仍然很好（7.93％，表6）。

但这种极深的模型仍然存在着开放的问题。这个1202层网络的测试结果比110层网络的测试结果更差，虽然两者都具有类似的训练误差。论文认为因为过拟合（overfifitting）。对于这种小型数据集，1202层网络可能是不必要的大（19.4M）。可以应用强大的正则化（regularization），如maxout[10]或者dropout[14]来获得最佳结果（[10,25,24,35]）。在本文中不使用maxout/dropout，只是简单地通过设计深且窄的架构简单地进行正则化，而不会分散集中在优化难点上的注意力。但结合更强的正规化可能会改善结果，作者表示将来会研究。

4.3. Object Detection on PASCAL and MS COCO

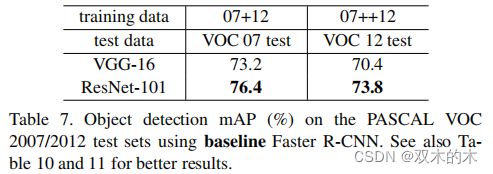
论文的方法对其他识别任务有很好的泛化性能（generalization performance）。表7和表8显示了PASCAL VOC 2007和2012[5]以及COCO[26]的目标检测基准结果。论文采用Faster R-CNN[32]作为检测方法。在这里，作者感兴趣的是用ResNet-101替换VGG-16[40]。使用这两种模式的检测实现（见附录）是一样的，所以收益只能归因于更好的网络。最显著的是，在有挑战性的COCO数据集中，COCO的标准度量指标（mAP@[.5，.95]）增长了6.0％，相对改善了28％。这种收益完全是由于学习表示（learned representations）。

表7。在PASCAL VOC 2007/2012测试集上使用基准Faster R-CNN的目标检测mAP(%)。更好的结果请看附录。

表8。在COCO验证集上使用基准Faster R-CNN的目标检测mAP(%)。更好的结果请看附录。

基于深度残差网络，网络在ILSVRC & COCO 2015竞赛的几个任务中获得了第一名，分别是：ImageNet检测，ImageNet定位，COCO检测，COCO分割。跟多细节请看附录（appendix）。

阅读论文真的挺花时间的，有好的方法欢迎大家评论区分享~~

说明：记录学习笔记，如果错误欢迎指正！写文章不易，转载请联系我。