隐HMM词性标注以及代码详解

# 简单实现HMM以及详细解释

import nltk
import sys
from nltk.corpus import brown	
brown_tags_words = [ ]

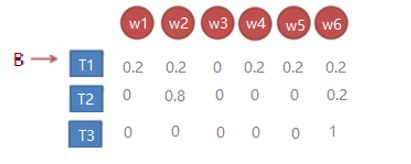
# P(tags | words) 正比于 P(ti | t{i-1}) * P(wi | ti) A * B (状态矩阵概率 * 发射概率)
# 这里需要做的预处理是：给词们加上开始和结束符号。
#
# Brown里面的句子都是自己标注好了的，长这个样子：(I , NOUN), (LOVE, VERB), (YOU, NOUN)
#
# 那么，我们的开始符号也得跟他的格式符合，我们用：(START, START) (END, END)

for sent in brown.tagged_sents():
    # 先加开头
    brown_tags_words.append( ("START", "START") )
    # 为了省事儿，我们把tag都省略成前两个字母
    brown_tags_words.extend([ (tag[:2], word) for (word, tag) in sent ])
    # 加个结尾
    brown_tags_words.append( ("END", "END") )


# B 发射概率
#P(wi | ti) = count(wi, ti) / count(ti) 这里NLTK给了我们做统计的工具
# conditional frequency distribution(条件频率分布) cfd_tagwords的数据结构为 {'JJ' ---> 'new' ---> 1060 }
cfd_tagwords = nltk.ConditionalFreqDist(brown_tags_words)
# conditional probability distribution(条件概率分布) {'JJ' ---> 'new' ---> 1060 ---> 1060/71994 = 0.0147}
cpd_tagwords = nltk.ConditionalProbDist(cfd_tagwords, nltk.MLEProbDist)
print("词性'JJ'转为 'new'的发射概率为:", cpd_tagwords["JJ"].prob("new"))
print("词性'VB'转为 'duck'的发射概率为:", cpd_tagwords["VB"].prob("duck"))

# A
brown_tags = [tag for (tag, word) in brown_tags_words ] #list ['start', 'AT','NP', 'NP']

# count(t{i-1} ti)
# bigram的意思是 前后两个一组，联在一起 P(ti | ti-1) = count(ti, ti-1) / count(ti)
cfd_tags= nltk.ConditionalFreqDist(nltk.bigrams(brown_tags))
# P(ti | t{i-1})
cpd_tags = nltk.ConditionalProbDist(cfd_tags, nltk.MLEProbDist)
# print(list(cpd_tags))

print("P('NN'|'DT') = ", cpd_tags["DT"].prob("NN"))
print("P('NN'|'VB') = ", cpd_tags["VB"].prob("NN"))

prob_tagsequence = cpd_tags["START"].prob("PP") * cpd_tagwords["PP"].prob("I") * \
    cpd_tags["PP"].prob("VB") * cpd_tagwords["VB"].prob("want") * \
    cpd_tags["VB"].prob("TO") * cpd_tagwords["TO"].prob("to") * \
    cpd_tags["TO"].prob("VB") * cpd_tagwords["VB"].prob("race") * \
    cpd_tags["VB"].prob("END")

print( "eq 序列 'I want to race' 的词性转换序列 'START PP VB TO VB END' 值为:", prob_tagsequence)

distinct_tags = set(brown_tags)

sentence = ["I", "want", "to", "race" ]
#sentence = ["I", "love", "you", "so","much" ]
viterbi = [ ]
backpointer = [ ]
path = []

# 前向传播，计算所有state（词性）转换的最佳路径
for wordindex in range(0, len(sentence)):
     # print(sentence[wordindex])
     this_viterbi = {}
     this_backpointer = {}
     for tag in distinct_tags:

         # START没有卵用的，我们要忽略
         if tag == "START":continue

         # 如果现在这个tag是X，现在的单词是w，
         # 我们想找前一个tag Y，并且让最好的tag sequence以Y X结尾。
         # 也就是说
         # Y要能最大化：
         # prev_viterbi[ Y ] * P(X | Y) * P( w | X)
         if wordindex == 0:
             #this_viterbi[ tag ] 为 路径的得分score[ 'DT' ]， sentence[0] = "I" ,cpd_tags["START"].prob(tag) 为转移概率，cpd_tagwords[tag].prob( sentence[0] ) 为发射概率
             # score[ 'DT' ] = P("DT"|"start") *  P("I" |"DT")
             this_viterbi[tag] = cpd_tags["START"].prob(tag) * cpd_tagwords[tag].prob(sentence[wordindex])# {'DT': 0.0, 'AT': 0.0, 'DO': 0.0, 'WD': 0.0, 'BE': 0.0, 'WP': 0.0, '``': 0.0, '.': 0.0,...}
             this_backpointer[tag] = "START"  # {'DT': 'START', 'AT': 'START', 'DO': 'START', 'WD': 'START',...}

         else:
             prev_viterbi = viterbi[-1]
             #把当前单词可选的词性 一一便利，并且全连接前面一层
             #eq I want to race。 当前词为to，to的词性有distinct_tags种，如 ['AT', 'NP', 'NN', 'JJ', 'VB', 'NR',...]，to的上一个词是 want，want页由distinct_tags种词性
             #当 to 便利第一个tag 即'AT'时， 'AT'与前一层want的词性['AT', 'NP', 'NN', 'JJ', 'VB', 'NR',...] 有1 * istinct_tags种可能，我们选择分数最高的。
             #分数最高的转换既是 best_previous
             best_previous = max(prev_viterbi.keys(),
                             key=lambda prevtag: \
                                 prev_viterbi[prevtag] * cpd_tags[prevtag].prob(tag) * cpd_tagwords[tag].prob(
                                     sentence[wordindex]))

             # 记录当前tag(词性)最分 this_viterbi[tag]
             this_viterbi[tag] = prev_viterbi[best_previous] * \
                                 cpd_tags[best_previous].prob(tag) * cpd_tagwords[tag].prob(sentence[wordindex])
             #把当前词性与前面连接最佳的路径存在 this_backpointer 中
             this_backpointer[tag] = best_previous

     # 每次找完Y 我们把目前最好的 存一下
     currbest = max(this_viterbi.keys(), key=lambda tag: this_viterbi[tag])
     print("Word", "'" + sentence[wordindex] + "'", "current best two-tag sequence:", this_backpointer[currbest],
           currbest)
     path.append(currbest)  # 记录路径
     # 完结
     # 全部存下来
     viterbi.append(this_viterbi)  # 把字典类型的this_viterbi放入list类型的viterbi
     backpointer.append(this_backpointer)  # 把字典类型的this_backpointer放入list类型的backpointer
print(path)


# 找所有以END结尾的tag sequence
prev_viterbi = viterbi[-1]
best_previous = max(prev_viterbi.keys(),
                    key = lambda prevtag: prev_viterbi[ prevtag ] * cpd_tags[prevtag].prob("END"))
# score[ 'END ] =score[ 'best_previous' ] * P("END"|"best_previous")
prob_tagsequence = prev_viterbi[ best_previous ] * cpd_tags[ best_previous].prob("END")

# 我们这会儿是倒着存的。。。。因为。。好的在后面
best_tagsequence = [ "END", best_previous ]
# 同理 这里也有倒过来 backpointer可以理解为一张二维的全连接的状态转换图，每一个状态都向前连接到它的最优路径
backpointer.reverse()

path_back = []
#反向回溯查找路径的每一给state（词性） 从END ----> START
current_best_tag = best_previous
for bp in backpointer:
    path_back.append(current_best_tag)
    best_tagsequence.append(bp[current_best_tag])
    current_best_tag = bp[current_best_tag]
path_back.reverse()

# path = ['START']
path = ['START'] + path_back +['END']

#词性序列的大小
prob_tagsequence = 1
#计算 序列 'I want to race' 的词性序列最大可能性的值
for i in range (0,len(sentence)+1):
    if i==0:#如果是序列的第一个词性
        pre = 'START'
        current = path_back[i]
    elif i == path_back.__len__():#在词性序列结构后加上’END‘
        pre = path_back[i - 1]
        current = 'END'
        # 'END' 的时候没有发射概率
        prob_tagsequence = prob_tagsequence * cpd_tags[pre].prob(current)
        break
    else:# P(current|pre)
        pre = path_back[i-1]
        current = path_back[i]

    prob_tagsequence = prob_tagsequence * cpd_tags[pre].prob(current) * cpd_tagwords[current].prob(sentence[i])

print( "序列 ",sentence," 的词性转换序列: ",path," = ", prob_tagsequence)