手撸HMM实现词性标注（Part-of-speech）

HMM系列文章：

隐马尔科夫模型（HMM）原理小结（1）
隐马尔科夫模型（HMM）原理小结（2）
手撸HMM实现词性标注（Part-of-speech）

本博客中使用到的完整代码请移步至: 我的github：https://github.com/qingyujean/Magic-NLPer，求赞求星求鼓励~~~

---

1. 环境准备

使用NLTK的Brown数据集，Brown语料中句子的形式，都是形如：[(I,NOUN), (Love, VERB), (You, NOUN)]， 即：(word,tag) 形式。

安装NLTK

pip3 install nltk

如果一切顺利，这意味着您已经成功地安装了NLTK库。首次安装了NLTK，需要在CMD中通过运行以下代码来安装NLTK扩展包：

import nltk
nltk.download()

如果是在windows上，则将弹出NLTK 下载窗口来选择需要安装哪些包（可以只选Brown语料，也可以全部安装）：

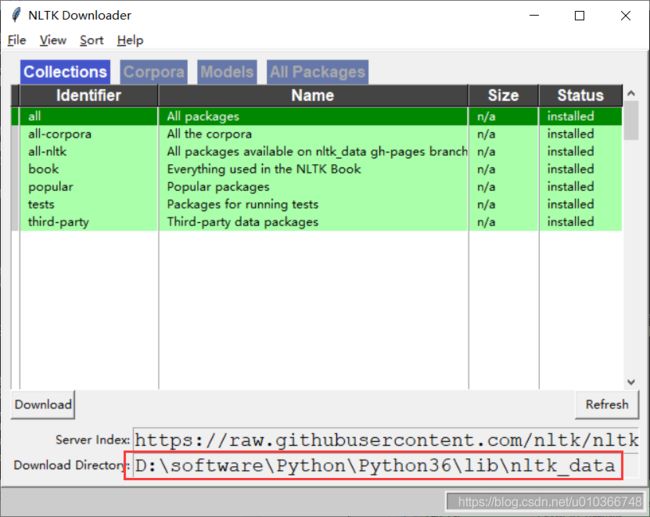
如果是在Linux上，则没有图形化界面，但是有交互命令，可以按如下流程选择Brown数据集下载。

2. 使用HMM 实现词性标注

目标：为一个句子，找到“最好”的词性标签。
$$\arg \underset{t_1{t}_2...t_N}{\max }P(t_1,...,t_N|w_1,...,w_N)\propto \arg \underset{t_1{t}_2...t_N}{\max }\prod _{i=1}^{N}P(t_i|t_{i-1})P(w_i|t_i)$$

先看一下brown语料中，句子的形式，都是形如：[(I,NOUN), (Love, VERB), (You, NOUN)]，
即：(word,tag) 形式

print(type(brown.tagged_sents()[0]), brown.tagged_sents()[0])

输出：

 [('The', 'AT'), ('Fulton', 'NP-TL'), ('County', 'NN-TL'), ('Grand', 'JJ-TL'), ('Jury', 'NN-TL'), ('said', 'VBD'), ('Friday', 'NR'), ('an', 'AT'), ('investigation', 'NN'), ('of', 'IN'), ("Atlanta's", 'NP$'), ('recent', 'JJ'), ('primary', 'NN'), ('election', 'NN'), ('produced', 'VBD'), ('``', '``'), ('no', 'AT'), ('evidence', 'NN'), ("''", "''"), ('that', 'CS'), ('any', 'DTI'), ('irregularities', 'NNS'), ('took', 'VBD'), ('place', 'NN'), ('.', '.')]

2.1 句子开始和结束标记

为语料中每个形如[(word,tag), (word,tag),…]的句子添加(, ) 和 (, )。

start_token = ''
end_token = ''

brown_tags_words = []
for sent in brown.tagged_sents():
    brown_tags_words.append((start_token, start_token))
    # brown_tags_words = brown_tags_words + sent # 这种写法性能极差
    # 交换word和tag的顺序，方便后面使用nltk的ConditionalFreqDist 条件频率计数工具
    brown_tags_words.extend([(t[:2],w) for (w,t) in sent]) # 简化词性 原始语料有470多种词性，太复杂
    brown_tags_words.append((end_token, end_token))

print(len(brown_tags_words))

输出：

1275872

2.2 问题2–HMM参数估计：统计词频计算概率

（1）发射概率估计

$${\hat{b}}_j(k)=P(w_n=k|t_n=j)=\frac{Count(w_n=k,t_n=j)}{Count(t_n=j)}$$

为了方便，这里直接使用nltk自带的统计工具。

# Calculate conditional frequency distribution 返回FreqDist对象的集合
# 返回的key是条件，即tag value是FreqDist对象 即词与词频
cfd_tagwords = nltk.ConditionalFreqDist(brown_tags_words) # count(wk, tj)
# 使用MLE（极大似然估计）计算conditional probability distribution，即用词频信息去计算概率
# 返回的key是条件 即tag，value是p(wk|tj)
cpd_tagwords = nltk.ConditionalProbDist(cfd_tagwords, nltk.MLEProbDist) # p(wk|tj)

print(len(cpd_tagwords))
print(cpd_tagwords.keys())

输出：

51
dict_keys(['', 'AT', 'NP', 'NN', 'JJ', 'VB', 'NR', 'IN', '``', "''", 'CS', 'DT', '.', '', 'RB', ',', 'WD', 'HV', 'CC', 'BE', 'TO', 'PP', 'DO', 'AP', 'QL', 'AB', 'WR', 'CD', 'MD', 'PN', 'WP', '*', 'EX', ':', '(', ')', 'RP', '--', 'OD', ',-', "'", '(-', ')-', 'FW', 'UH', ':-', '.-', '*-', 'WQ', 'RN', 'NI'])

print("The probability of an adjective (JJ) being 'new' is", cpd_tagwords['JJ'].prob('new'))
print("The probability of a verb (VB) being 'duck' is", cpd_tagwords['VB'].prob('duck'))

输出：

The probability of an adjective (JJ) being 'new' is 0.01472344917632025
The probability of a verb (VB) being 'duck' is 6.042713350943527e-05

（2）转移概率估计

$${\hat{a}}_{ij}=P(t_{n+1}=j|t_n=i)=\frac{Count(t_n=i,t_{n+1}=j)}{Count(t_n=i)}$$

（3）初始状态概率分布

$${\hat{\pi }}_i=P(t_1=i|t_0{=}^{\prime }star{t}^{\prime })=\frac{Count(t_0{=}^{\prime }star{t}^{\prime },t_1=i)}{Count(t_0{=}^{\prime }star{t}^{\prime })}$$

brown_tags = [t for (t,w) in brown_tags_words] # 取出所有tag
# Calculate conditional frequency distribution 返回FreqDist对象的集合
# 返回的key是条件，即tag value是FreqDist对象 即tag与频率 （bigram tag）
cfd_tags = nltk.ConditionalFreqDist(nltk.bigrams(brown_tags)) # count(t{i-1}, ti)
# print(cfd_tags.keys())
# print(cfd_tags['']['NN'])
# 返回的key是条件 即tag，value是p(ti|t{i-1})
cpd_tags = nltk.ConditionalProbDist(cfd_tags, nltk.MLEProbDist) # p(ti|t{i-1})
# print(cpd_tags.keys())
# print(cpd_tags[''].prob('NN'))

print("If we have just seen 'DT', the probability of 'NN' is", cpd_tags["DT"].prob("NN"))
print( "If we have just seen 'VB', the probability of 'JJ' is", cpd_tags["VB"].prob("DT"))
print( "If we have just seen 'VB', the probability of 'NN' is", cpd_tags["VB"].prob("NN"))

输出：

If we have just seen 'DT', the probability of 'NN' is 0.5057722522030194
If we have just seen 'VB', the probability of 'JJ' is 0.016885067592065053
If we have just seen 'VB', the probability of 'NN' is 0.10970977711020183

问题1–求解观测序列概率

给出一个句子：‘I want to race’ ，它与tag 序列：‘PP VB TO VB’ 匹配度有多高呢？

其实就是求：$P(w_1,w_2,...,w_N,t_1,t_2,...,t_N)\approx P(t_0)\prod _{i=1}^{N}P(t_i|t_{i-1})P(w_i|t_i)$

所以匹配度即概率为：
$$\begin{array}{rl}P(start)\ast & P(PP|start)\ast P(I|PP)\ast \\ & P(VB|PP)\ast P(want|VB)\ast \\ & P(TO|VB)\ast P(to|TO)\ast \\ & P(VB|TO)\ast P(race|VB)\ast \\ & P(end|VB)\end{array}$$

【注意】：p(start)=1

prob_of_tagsentences = cpd_tags[''].prob('PP') * cpd_tagwords['PP'].prob('I') * \
    cpd_tags['VB'].prob('PP') * cpd_tagwords['VB'].prob('want') * \
    cpd_tags['TO'].prob('VB') * cpd_tagwords['TO'].prob('to') * \
    cpd_tags['VB'].prob('TO') * cpd_tagwords['VB'].prob('race') * \
    cpd_tags[''].prob('VB')
print("The probability of the tag sequence 'START PP VB TO VB END' for 'I want to race' is:", prob_of_tagsentences)

输出：

The probability of the tag sequence ' PP VB TO VB ' for 'I want to race' is: 0.0

2.3 问题3–预测问题：vitervi算法实现

解决问题3：已知一个句子，求解最符合的tags序列

• （1）初始化
• （2）递推
• （3）终止
• （4）最优路径回溯

（1）初始化

# 先拿出所有的tags
distinct_tags = set(brown_tags)

sentence = ["I", "want", "to", "race"]

sent_len = len(sentence)

score = [] # best path score
backpointer = [] # 记录best path 节点的前一个节点

# （1）初始化
first_score = {}
first_backpointer = {}
# 初始化score 和 backpointer
for tag in distinct_tags:
    if tag == '': # 没有以start结尾的句子
        continue
    # score[t1,w1]=p(start) * p(t1|start) * (w1|t1)=1*p(t1|start) * (w1|t1)
    # 或者\delta_{1}(i)=\pi_{i} b_{i}(o_{1})
    p_t1_c_start = cpd_tags[''].prob(tag) * cpd_tagwords[tag].prob(sentence[0])
    first_score[tag] = p_t1_c_start
    first_backpointer[tag] = ''

# 得到第一个“最优”子路径和第一个回溯点
print(first_score)
print(first_backpointer)

输出：

{'WR': 0.0, 'NP': 1.7319067623793952e-06, 'CD': 0.0, ':-': 0.0, '(-': 0.0, ')': 0.0, 'AB': 0.0, ',': 0.0, '.-': 0.0, '*-': 0.0, 'OD': 0.0, 'DO': 0.0, '*': 0.0, 'CC': 0.0, 'FW': 0.0, 'WQ': 0.0, 'IN': 0.0, 'MD': 0.0, 'RP': 0.0, 'QL': 0.0, 'EX': 0.0, "'": 0.0, '.': 0.0, 'RN': 0.0, 'RB': 0.0, "''": 0.0, 'WP': 0.0, 'DT': 0.0, 'BE': 0.0, 'AP': 0.0, 'PN': 0.0, 'WD': 0.0, '``': 0.0, 'TO': 0.0, 'HV': 0.0, 'CS': 0.0, 'VB': 0.0, '(': 0.0, ')-': 0.0, '--': 0.0, ',-': 0.0, 'UH': 0.0, 'PP': 0.014930900689060006, 'AT': 0.0, ':': 0.0, 'NN': 1.0580313619573935e-06, 'NR': 0.0, 'NI': 3.3324520848931064e-07, 'JJ': 0.0, '': 0.0}
{'WR': '', 'NP': '', 'CD': '', ':-': '', '(-': '', ')': '', 'AB': '', ',': '', '.-': '', '*-': '', 'OD': '', 'DO': '', '*': '', 'CC': '', 'FW': '', 'WQ': '', 'IN': '', 'MD': '', 'RP': '', 'QL': '', 'EX': '', "'": '', '.': '', 'RN': '', 'RB': '', "''": '', 'WP': '', 'DT': '', 'BE': '', 'AP': '', 'PN': '', 'WD': '', '``': '', 'TO': '', 'HV': '', 'CS': '', 'VB': '', '(': '', ')-': '', '--': '', ',-': '', 'UH': '', 'PP': '', 'AT': '', ':': '', 'NN': '', 'NR': '', 'NI': '', 'JJ': '', '': ''}

看看当前最好的tag是哪一个：

# 看看目前最好的tag是哪一个？
curr_best = max(first_score.keys(), key=lambda tag: first_score[tag])
print( "Word", "'" + sentence[0] + "'", "current best two-tag sequence:", first_backpointer[curr_best], curr_best)

输出：

Word 'I' current best two-tag sequence:  PP

将第一个节点加入score和backpointer：

# 将第一个节点加入score和backpointer
score.append(first_score)
backpointer.append(first_backpointer)

（2）递推

# （2）递推
# 完成初始化了，就可以开始inductive 递推了
for i in range(1, sent_len):
    this_score = {}
    this_backpointer = {}
    prev_score = score[-1] # 所有的前驱节点的score score表示了到该点截至，目前最优路径的score

    for tag in distinct_tags:
        if tag == '':
            continue
        best_prevtag = max(prev_score.keys(), key=lambda prevtag: prev_score[prevtag] * \
                                                               cpd_tags[prevtag].prob(tag) * \
                                                               cpd_tagwords[tag].prob(sentence[i]))
        this_score[tag] = prev_score[best_prevtag] * cpd_tags[best_prevtag].prob(tag) * \
                          cpd_tagwords[tag].prob(sentence[i])
        this_backpointer[tag] = best_prevtag

    # 我们把当前最好的tag打印一下
    curr_best = max(this_score.keys(), key = lambda tag: this_score[tag])
    print( "Word", "'" + sentence[i] + "'", "current best two-tag sequence:", this_backpointer[curr_best], curr_best)

    # 将当前节点加入score和backpointer
    score.append(this_score)
    backpointer.append(this_backpointer)

输出：

Word 'want' current best two-tag sequence: PP VB
Word 'to' current best two-tag sequence: VB TO
Word 'race' current best two-tag sequence: IN NN

（3）终止

找所有以结尾tag_sequence， score中最大值：

# （3）终止
# 找所有以结尾tag_sequence， score中最大值
prev_score = score[-1]
best_prevtag = max(prev_score.keys(), key=lambda prevtag: prev_score[prevtag] * \
                                                               cpd_tags[prevtag].prob('')
                   )
best_score = prev_score[best_prevtag] * cpd_tags[best_prevtag].prob('')
print('best_score:', best_score)

输出：

best_score: 5.71772824864617e-14

结果不是很好，说明要加更多的语料。

（4）最优路径回溯

# （4）最优路径回溯
best_tag_seqs = ['', best_prevtag] # 准备开始
curr_best_tag = best_prevtag
for bp in backpointer[::-1]: # 从后往前tracking
    best_tag_seqs.append(bp[curr_best_tag])
    curr_best_tag = bp[curr_best_tag]

best_tag_seqs.reverse()

print('The sentence was:', sentence)
print('The best tag sequence is:', best_tag_seqs)

输出：

The sentence was: ['I', 'want', 'to', 'race']
The best tag sequence is: ['', 'PP', 'VB', 'IN', 'NN', '']

print( "The probability of the best tag sequence is:", best_score)

输出：

The probability of the best tag sequence is: 5.71772824864617e-14

结果不是很好，说明要加更多的语料。

完整代码地址

完整代码请移步至: 我的github：https://github.com/qingyujean/Magic-NLPer，求赞求星求鼓励~~~

最后：如果本文中出现任何错误，请您一定要帮忙指正，感激~