|Boids|鸟群模型|鸟群算法|学习笔记 - 论文学习
本文基于Craig Reynolds于1986年发布的《Flocks, Herds, and Schools: A Distributed Behavioral Model》进行学习和总结
通过一段原文,一段分析的方法,进行分析
概述
摘要
The aggregate motion of a flock of birds, a herd of land animals, or a
school of fish is a beautiful and familiar part of the natural world.
But this type of complex motion is rarely seen in computer animation.
This paper explores an approach based on simulation as an alternative
to scripting the paths of each bird individually. The simulated flock
is an elaboration of a particle system, with the simulated birds being
the particles. The aggregate motion of the simulated flock is created
by a distributed behavioral model much like that at work in a natural
flock; the birds choose their own course. Each simulated bird is
implemented as an independent actor that navigates according to its
local perception of the dynamic environment, the laws of simulated
physics that rule its motion, and a set of behaviors programmed into
it by the “animator.” The aggregate motion of the simulated flock is
the result of the dense interaction of the relatively simple behaviors
of the individual simulated birds.
首先作者为我们介绍了,在自然界之中,无论是鸟群、鱼群还是陆地生物群落,它们的群体性运动都是非常壮观的,然而在动画领域(当时)却极少的出现。因此这篇论文提出了一种基于模拟的方法,用它来模拟每个独立个体的运动路径。这个模拟出来的模型跟自然中的鸟群运动模型十分相似,每个小鸟都是一个独立的角色。通过对动态环境的感知,物理定律来模拟运动,以及绘图程序这三部分,来实现这样一个运动感知模型 。
并向我们阐述了模型的运行逻辑,模拟鸟群的整体运动是模拟鸟群个体相对简单行为密集相互作用的结果。即,个体相互作用以影响整体。
·
简介
The motion of a flock of birds is one of nature’s delights. Flocks and related synchronized group behaviors such as schools of fish or herds of land animals are both beautiful to watch and intriguing to contemplate. A flock* exhibits many contrasts. It is made up of discrete birds yet overall motion seems fluid; it is simple in concept yet is so visually complex, Permission to copy without fee all or part of this material is granted provided that the copies are not made or distributed for direct it seems randomly arrayed and yet is magnificently synchronized. Perhaps most puzzling is the strong impression of intentional, centralized control. Yet all evidence indicates that flock motion must be merely the aggregate result of the actions of individual animals, each acting solely on the basis of its own local perception of the world.
第一段,作者给我们通俗的介绍了一下自然中鸟群的运动,以及通过计算机编程、绘图进行实现。这个模型是由离散的鸟类个体组成的,在整体上表现出流动性。作者认为这个概念易于理解和实现,但是完成视觉实现却很复杂。这个模型在是由离散的鸟类随机排列的,但却非常的同步。群体运动是个体动物行为的总和,每一种个体的行为都基于该个体对于世界的局部认知。
·
·
One area of interest within computer animation is the description and control of all types of motion. Computer animators seek both to invent wholly new types of abstract motion and to duplicate (or make variations on) the motions found in the real world. At first glance, producing an animated, computer graphic portrayal of a flock of birds presents significant difficulties. Scripting the path of a large number of individual objects using traditional computer animation techniques would be tedious. Given the complex paths that birds follow, it is doubtful this specification could be made without error. Even if a reasonable number of suitable paths could be described, it is unlikely that the constraints of flock motion could be maintained (for example, preventing collisions between all birds at each frame). Finally, a flock scripted in this manner would be hard to edit (for example, to alter the course of all birds for a portion of the animation). It is not impossible to script flock motion, but a better approach is needed for efficient, robust, and believable animation of flocks and related group motions.
第二段为我们介绍了计算机动画领域以及对于鸟群模型的动画实现。对于鸟群动画的电脑制作是很复杂的,如果用传统的动画技术,为大量的单个对象的路径编写脚本是乏味的。同时,在考虑了在整体鸟群模型中,个体所分别遵循的复杂的路径,这个方法能否正确实现也是值得怀疑的。因此传统方法实现的鸟群模型很难去编写。这里就作者就提出了需要一种高效、鲁棒性和可信性强的鸟群制作、绘制方法。
This paper describes one such approach. This approach assumes a flock is simply the result of the interaction between the behaviors of individual birds. To simulate a flock we simulate the behavior of an individual bird (or at least that portion of the bird’s behavior that allows it to participate in a flock). To support this behavioral “control structure” we must also simulate portions of the bird’s perceptual mechanisms and aspects of the physics of aerodynamic flight. If this simulated bird model has the correct flock-member behavior, all that should be required to create a simulated flock is to create some instances of the simulated bird model and allow them to interact.
这里就是关于作者提出的Boids模型的概述。**假设鸟群只是单个鸟类行为相互作用的结果。**为了模拟鸟群,我们模拟一只鸟的行为(或者至少是那只鸟参与鸟群的部分行为)。为了支持这种行为“控制结构”,我们还必须模拟鸟类的部分感知机制和空气动力飞行的物理方面。如果这个模拟的鸟类模型具有正确的鸟群成员行为,那么创建一个模拟的鸟群所需要的就是创建一些模拟的鸟类模型的实例,并允许它们进行交互。通过对单个个体不断施加条件,通过个体的运动模拟出对鸟群的整体运动。
Some experiments with this sort of simulated flock are described in more detail in the remainder of this paper. The suc-cess and validity of these simulations is difficult to measure objectively. They do seem to agree well with certain criteria [25] and some statistical properties [23] of natural flocks and schools which have been reported by the zoological and behavioral sciences. Perhaps more significantly, many people who view these animated flocks immediately recognize them as a representation of a natural flock, and find them similarly delightful to watch.
模型模拟的准确性和有效性很难去客观的衡量。模拟出的动物群体会符合动物学和行为学研究和报到出的统计学规律,更重要的是人们看到这些群体的模拟动画时,可以立刻就认出这是自然的群落,并且发现这是很赏心悦目的。
·
·
·
·
在作者开始关于Boids模型的规则推导之前,首先进行了一些的准备工作。
分不同的点进行介绍了一下几个方面。
颗粒模型是作者对比已有模型,对自己提出的Boids模型进行说明。
同时,吸收并应用了参与者和分布式模型的相关理论。
而力场群聚,行为动画,几何飞行以及Turtles都是用于实现模型绘制的准备工作。
·
·
力场群聚
这一部分叙述了是如何通过力场这一物理概念,他们是如何产生作用的,进而对整个群体产生对应的作用。
在这里我们主要分析一下它的核心段落。
如下:
That animation was produced using a technique completely unlike the one described in this paper and apparently not specifically intended for flock modeling. But the underlying concept is useful and interesting in its own right. The following overview is based on unpublished communications [3]. The software is informally called “the force field animation sys- tem.” Force fields are defined by a 3 x 3 matrix operator that transform from a point in space (where an object is located) to an acceleration vector; the birds trace paths along the “phase portrait” of the force field. There are “rejection forces” around each bird and around static objects. The force field associated with each object has a bounding box, so object interactions can be culled according to bounding box tests. An incremental, linear time algorithm finds bounding box intersections. The “animator” defines the space field(s) and sets the initial positions, orientations, and velocities of objects. The rest of the simulation is automatic.
其向我们介绍了,在模拟群聚中,个体力场的数学描述。在后续的计算机程序中,也对其进行实现。文章这样写道:力场由一个3×3的矩阵运算定义,将从该点到空间中的一点转换为一个加速度矢量;鸟沿着力场的“相位图”来追踪路径。
在每个鸟和静态物体的周围都有排斥力。与每一个物体相关联的力场都有一个边界,因此可以根据边界框测试来实现物体边界的相互作用。线性时间增量算法可以计算边界框之间的交点。通过动画来定义空间场,并设定物体的初始位置、方向和速度(其实就是位置矢量和速度矢量)。其余的模拟都是自动进行的。
粒子系统
Underlying the bold flock model is a slight generalization of particle systems. In what might be called a “subobject sys- tem,” Reeves’s dot-like particles are replaced by an entire geometrical object consisting of a full local coordinate system and a reference tO a geometrical shape model. The use of shapes instead of dots is visually significant, but the more fundamental difference is that individual subobjects have a more complex geometrical state: they now have orientation.
Another difference between bold flocks and particle systems is not as well defined. The behavior of boids is generally more complex than the behaviors for particles as described in the literature. The present bold behavior model might be about one or two orders of magnitude more complex than typical particle behavior. However this is a difference of degree, not of kind. And neither simulated behavior is nearly as complex as that of a real bird.
这里我们着重分析这两段。
作者在这部分主要是想通过和另一个已有的相似模型,颗粒系统。进行对比介绍。
模拟群和粒子系统联系是十分紧密的。作者这里介绍了粒子系统的构成和属性。粒子系统的实现有火、烟、云等等。粒子系统是大量单个粒子的集合,每个粒子都有自己的行为。粒子会被创造、老化和消亡。他们由特定的行为可以改变自己的状态,包括颜色、不透明度、位置和速度。
在Boids群体模型之下,是对粒子系统的一种概括。 在所谓的“子对象系统”中,点状粒子被一个由完整的局部坐标系统和一个几何形状模型的参考组成的整个几何对象所取代。使用形状而不是圆点在视觉上很重要,但更根本的区别在于单个子对象有更复杂的几何状态:它们现在有了方向。
二者的另一个区别在Boids模型和粒子系统模型还没有很好的界定。Boids的行为通常比文献中描述的粒子的行为更复杂。目前的Boids模型可能比典型的粒子行为复杂一到两个数量级。然而,这只是程度上的不同,而不是性质上的不同。虽然,这两种模拟行为都没有真正的鸟类复杂。
二者最明显的区别是粒子系统中的粒子并不会产生相互作用,而Boids中,鸟类是通过个体间较强的相互作用才能正确的聚集在一起。Boids行为同时依赖于内部状态和外部状态。
参与者和分布式系统
The behavioral model that controls the boid’s flight and flocking is complicated enough that rather than use an ad hoc approach, it is worthwhile to pursue the most appropriate formal computational model. The behaviors will be represented as rules or programs in some sense, and the internal state of each bold must be held in some sort of data structure. It is convenient to encapsulate these behaviors and state as an object, in the sense of object-oriented programming systems [10, 11, 21]. Each instance of these objects needs a computational process to apply the behavioral programs to the internal data. The computational abstraction that combines process, procedure, and state is called an actor [12, 26, 2]. An actor is essentially a virtual computer that communicates with other virtual computers by passing messages. The actor model has been proposed as a natural structure for animation control by several authors [28, 13, 29, 18]. It seems particularly apt for situations involving interacting characters and behavior simulation. In the literature of parallel and distributed computer systems, flocks and schools are given as examples of robust self-organizing distributed systems [15].
实现Boids模型同时需要了数学、物理等理论支撑、编程实现相应的原理、最后通过计算机绘图技术绘制。在这一部分,作者为我们介绍了一种对应的编程实现手法。
用于控制Boids的模型已经足够的复杂,如果再使用新的实现方法,不如寻找一个已有的最符合的方法。在面向对象的编程变成系统之上,可以将这些数据进行封装于对象之中。并结合过程、过程期间和状态抽象为一个角色,”actor”。该角色模型已经被他的作者赋予了动画控制的自然结构。而且这种结构更适合于设计互动角色和行为模拟的情景。更重要的是在并行和分布式的计算机系统文献之中,群落运动也被作为自组织分布式系统的例子。
行为动画
Traditional hand-drawn eel animation was produced with a medium that was completely inert. Traditional computer animation uses an active medium (computers running graphics software), but most animation systems do not make much use of the computer’s ability to automate motion design.
The animator cannot simply tell the character to “act happy” but must tediously specify the motion that conveys happiness.
首先,作者为我们介绍了传统的动画模式。这种动画模式是以一种完全惰性的媒介制作的。但是和现代化相比,其需要较为复杂和冗长的指令才能表达Boids所需要的内容。在这方面所展现的弊端,使其不适合于Boids动画的制作,因此实现Boids模型需要新型的动画制作。
Typical computer animation models only the shape and physical properties of the characters, whereas behavioral or character-based animation seeks to model the behavior of the character. The goal is for such simulated characters to handle many of the details of their actions, and hence their motions.
在典型的电脑动画制作之中,电脑动画只模拟角色的形状和物理属性,而行为或基于角色的动画试图模拟角色的行为。我们需要达到的目标是,处理角色的行为以达到,从简单的路线规划到复杂的情感互动。
These behaviors, when acted out by the simulated characters, lead indirectly to the final action.
One of the charming aspects of the work reported here is not knowing how a simulation is going to proceed from the specified behaviors and initial conditions; there are many unexpected, pleasant surprises. On the other hand, this charm starts to wear thin as deadlines approach and the unexpected annoyances pop up. This author has spent a lot of time recently trying to get uncooperative flocks to move as intended
我们知道,Boids模型是一个由个体影响到总体的过程。因此,当这些角色被模拟出来的时候,就会间接的影响到最终行动。在模拟并运行的过程中,在特定的行为和初始条件进行时,会产生许多意想不到的惊喜。另一方面,由于是自主规划路线,因此细微的参数就会导致和预期结果不同。
几何飞行
Boids模型中的一个基本部分是飞行的几何能力。无论是鱼群还是陆地动物,都可以近似抽象出一种“飞行”的运动。当然,对于陆地动物,是一种限制了第三维度的自由运动。
In this paper the term geometric flight refers to a certain type of motion along a path: a dynamic, incremental, rigid geometrical transformation of an object, moving along and tangent to a 3D curve. While the motion is rigid, the ob- ject’s underlying geometric model is free to articulate or change shape within this “flying coordinate system.” Unlike more typical animated motion along predefined spline curves, the shape of a flight path is not specified in advance.
在本文中,“几何飞行”一词指的是沿着路径的某种类型的运动:**一个物体的动态、增量、刚性几何变换,沿着三维曲线移动并与之相切。**不同于更典型的沿着预定义路径的曲线的动画运动,飞行路径的形状不是预先指定的。
几何飞行的是基于物体的正向的局部的正Z轴增量而平移。

围绕着局部的X轴和Y轴进行旋转,从而重新调整Z轴的全局方向。在真正的飞行中,旋转和平移总是同时进行的。增量的的几何飞行是一个离散的近似,通过用不同的帧来将他们联系在一起。在动画的绘制过程中,就要求较高的帧率刷新以减少离散化运动的误差,并细化运动模糊模式的形状。
Geometric flight is based on incremental translations along the objecrs “forward direction” its local positive Z axis. These translations are intermixed with steering–rotations about the local X and Y axes (pitch and yaw), which realign the global orientation of the local Z axis.
Running the simulation at a higher rate can reduce the discrete sampling error of the flight model and refine the shape of motion blur patterns.
飞行建模广泛的应用了自身的坐标系。局部的空间代表boid的视角,这意味着以boid个体自身的位置和方向测量事物。在笛卡尔术语中,左右是x轴,前后是y轴,上下是z轴。通过应用局部比例尺,使坐标系的长度是一个单位的体长。
Geometric flight models conservation of momentum. An object in flight tends to stay in flight. There is a simple model of viscous speed damping, so even if the bold continually ac- celerates in one direction, it will not exceed a certain maximumspeed. A minimum speed can also be specified but defaults to zero. A maximum acceleration, expressed as a fraction of the maximum speed, is used to truncate over-anxious requests for acceleration, hence providing for smooth changes of speed and heading. This is a simple model of a creature with a finite amount of available energy.
几何飞行模型满足动量守恒。飞行中的物体往往会滞留在飞行中。这种粘滞速度的阻力有一个简单的模型,因此即使在一个方向中连续加速,也不会超过最大值速度。也可以指定一个最小的速度,一般这个速度被默认为0.最大加速度,表示为最大速度的一个小部分,用来限制速度的过分提升,用于提供一个平稳的速度和方向变化。
Many physical forces are not supported in the current bold model. Gravity is modeled but used only to define banking behavior. It is defined procedurally to allow the construction of arbitrarily shaped fields. If each bold was accelerated by gravity each frame, it would tend to fall unless gravity was coun- tered by lift or buoyancy. Buoyancy is aligned against gravity, but aerodynamic lift is aligned with the boid’s local “up” direction and related to velocity. This level of modeling leads to effects like normally level flight, going faster when flying down (or slower up), and the “stall” maneuver. The speed limit parameter could be more realistically modeled as a frictional drag, a backward pointing force related to velocity. In the current model steering is done by directing the available thrust in the appropriate direction. It would be more realistic to separately model the tangential thrusting forces and the lateral steering forces, since they normally have different magnitudes.
许多的物理力学在Boids模型中还没有得到支持。
重力仅仅被应用于在倾斜过程中的行为,它被程序定义为允许任意改变形状的场的构造。如果让Boid在飞行过程中的每一帧都受重力的影响,它将倾向于下落,除非重力被升力或者是浮力抵消(当然在陆地生物就不涉及这一影响)。
空气动力的升力与重力相互抵消,使其更像正常情况下的水平飞行。在上述的速度限制中,可以更真实的建立一个空气阻力模型,一个有关速度向后的指向力。在目前的模型中,转向是通过适当的方向上引导可用的推力来实现的。由于切向推力和法向的转向向心力不同,让这个建模更加真实。
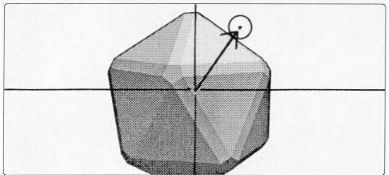
飞行中的倾斜
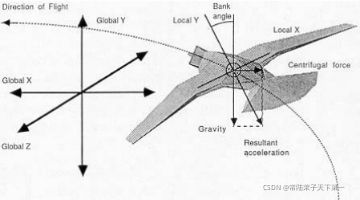
在几何飞行过程中,涉及平移、俯仰和偏航。在飞行过程中的Boid个体会随着飞行中的离心力作用下,产生倾斜运动。
当旋转时,径向分量变大,“加速度向下”方向向外摆动,就像一个悬挂在飞行物体上的钟摆。转弯加速度的大小与物体的速度和路径的曲率成正比(与转弯半径成反比)。
有了这样正确的倾斜,物体的局部空间内依旧保持着与感知和加速坐标系的统一。这样有一下几个优点:简化了boid个体的定位任务;在动画中,符合观众预期的飞行物体的移动和定位自己。
飞鸟与海龟(Turtles)
The incremental mixing of forward translations and local rotations that underlies geometric flight is the basis of “turtle graphics” in the programming language Logo.
Under program control the Logo turtle could move forward or back from its current position, turn left or right from its current heading, or put the pen up or down on the paper. The turtle geometry has been extended from the plane onto arbitrary manifolds and into 3D space [1]. These “3d turtles” and their paths are exactly equivalent to the boid objects and their flight paths.
几何飞行的基础是正向平移和局部旋转的增量混合,这是编程语言Logo中的“海龟图形”的基础。在程序控制下,Logo海龟可以从当前位置向前或向后移动,从当前标题向左或向右转,或在纸上放置笔。当海龟绘制的平面结构从二维推广到三维,他们所绘制的曲线就和boids的飞行路线完全相重合。
自然中的鸟群、羊群和鱼群
从这一部分开始是本文的重点部分,是作者对于Boids模型的理论架构。
For a bird to participate in a flock, it must have behaviors that allow it to coordinate its movements with those of its flockmates. These behaviors are not particularly unique; all creatures have them to some degree. Natural flocks seem to consist of two balanced, opposing behaviors: a desire to stay close to the flock and a desire to avoid collisions within the flock. It is clear why an individual bird wants to avoid collisions with its flockrnates. But why do birds seem to seek out the airborne equivalent of a nasty traffic jam? The basic urge to join a flock seems to be the result of evolutionary pressure from several factors: protection from predators, statistically improving survival of the (shared) gene pool from attacks from predators, profiting from a larger effective search pattern in the quest for food, and advantages for social and mating activities .
自然中的群落由两种平衡而相悖的因素组成:一种是想要靠近群落,另一种是想要避免群落内部的冲突。
基本要求加入一群似乎进化压力的结果从几个因素:保护天敌,统计上改善生存基因库的攻击捕食者,得益于一个更大的有效搜索模式在寻求食物,和优势为社会和交配活动。
There is no evidence that the complexity of natural flocks is bounded in any way. Flocks do not become “full” or “over- loaded” as new birds join. When herring migrate toward their spawning grounds, they run in schools extending as long as 17 miles and containing millions of fish . Natural flocks seem to operate in exactly the same fashion over a huge range of flock populations. It does not seem that an individual bird can be paying much attention to each and every one of its flock- mates. But in a huge flock spread over vast distances, an individual bird must have a localized and filtered perception of the rest of the flock. A bird might be aware of three categories: itself, its two or three nearest neighbors, and the rest of the flock .
没有证据表明鸟群的复杂度受到限制。我们可以通俗的认为,鸟群不会因为个体数量的增加,达到所谓的满载状态。自然的鸟群似乎在很大范围的鸟群中以完全相同的方式运作。一只鸟似乎不可能对它的每一个同伴都给予太多的关注。在一个分布很广的鸟群之中,单独的个体需要拥有局部性的认知。那么我们认定鸟群中的个体只可以了解三种物体:它自己,距离它最近的三个邻居,以及鸟群中的其他生物。
These speculations about the “computational complexity” of flocking are meant to suggest that birds can flock with any number of flockmates because they are using what would be called in formal computer science a constant time algorithm. That is, the amount of “thinking” that a bird has to do in order to flock must be largely independent of the number of birds in the flock. Otherwise we would expect to see a sha W upper bound on the size of natural flocks when the individual birds became overloaded by the complexity of their navigation task. This has not been observed in nature.
上述关于群体复杂度的计算保证了鸟类可以满足任意数量的群体聚集在一起,因为现实中的鸟类使用的是一个复杂度为常数的算法O(1)。也就是说一只鸟所在群体中的思考时间与群体中鸟类的总数量是相对独立的。否则就会因为,鸟群个体数量过大而导致超时,从而产生一个鸟群个体数量上限,在自然界中我们显然没有见过鸟群受数量的限制。
对比真实鸟群和模拟鸟群对复杂性的不敏感性。在计算机模拟的过程中,因为要遍历鸟群中的所有个体,因此所描述的集群算法的复杂度是O(n2)。也就是说,在运行过程中,的确存在鸟群是数量的一个上限。
模拟鸟群 ※
这一部分是本文最核心的部分,同时也对群智能算法做出了很大的贡献。
三原则:
分离 Separation: 移动以避开群体拥挤处
对齐 Alignment: 朝着周围同伴的平均方向前进
靠近 Cohesion: 朝着周围同伴的平均位置(质心)移动
- Collision Avoidance: avoid collisions with nearby
flockmates- Velocity Matching: attempt to match velocity with nearby flockmates
- Flock Centering: attempt to stay close to nearby flockmates
三种关系的示意图如下:
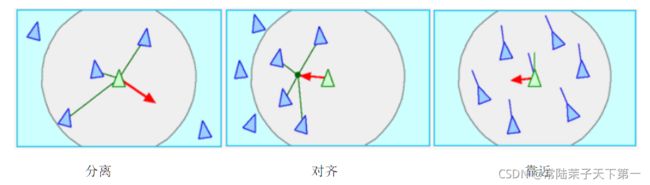
这也是这一论文对后来的研究贡献最大的部分。
下面是关于三原则的详细解释:
Velocity is a vector quantity, referring to the combination of heading and speed. The manner in which the results from each of these behaviors is reconciled and combined is significant and is discussed in more detail later. Similarly, the meaning nearby in these rules is key to the flocking process. This is also discussed in more detail later, but generally one boid’s awareness of another is based on the distance and direction of the offset vector between them.z
对齐。对齐是通过速度匹配所实现的。速度是一个由方向和速度大小所描述的矢量。一般来说,两个个体之间的感知是基于它们的偏移向量之间的距离和方向。
Static collision avoidance and dynamic velocity matching are complementary. Together they ensure that the members of a simulated flock are free to fly within the crowded skies of the flock’s interior without running into one another. Collision avoidance is the urge to steer away from an imminent impact. Static collision avoidance is based on the relative position of the flockmates and ignores their velocity. Conversely, velocity matching is based only on velocity and ignores position. It is a predictive version of collision avoidance: if the boid does a good job of matching velocity with its neighbors, it is unlikely that it will collide with any of them any time soon. With velocity matching, separations between boids remains approximately invariant with respect to ongoing geometric flight. Static collision avoidance serves to establish the minimum required separation distance; velocity matching tends to maintain it.
静态的分离和动态的对齐二者之间是互补的。它们的共同作用保证了鸟群的成员可以自由的在其个体内部拥挤的空间内飞行,而不会产生碰撞。静态的避碰是基于距离最近的三个邻居的相对位置,而忽略他们的速度。相反动态的速度匹配是只考虑它们的速度。这是一种通过预测维持鸟群的方式:如果个体能很好地匹配它的邻居的速度,那么它在短时间内不太可能与任何邻居发生碰撞。通过速度匹配,相对于持续的几何飞行,个体之间的分离保持近似不变。静态避碰是为了建立最小所需的分离距离;而速度匹配会维持它。
Flock centering makes a boid want to be near the center of the flock. Because each boid has a localized perception of the world, “center of the flock” actually means the center of the nearby flockmates. Flock centering causes the boid to fly in a direction that moves it closer to the centroid of the nearby boids. If a boid is deep inside a flock, the population density in its neighborhood is roughly homogeneous; the boid density is approximately the same in all directions. In this case, the cem troid of the neighborhood boids is approximately at the center of the neighborhood, so the flock centering urge is small. But if a boid is on the boundary of the flock, its neighboring boids are on one side. The centroid of the neighborhood boids is displaced from the center of the neighborhood toward the body of the flock. Here the flock centering urge is stronger and the flight path will be deflected somewhat toward the local flock center.
群聚使每一个鸟群都想靠近群落的中心。因为个体对世界都有一个局部的感知,“鸟群中心”实际上意味着附近的鸟群伙伴的中心。鸟群居中使飞行体朝更接近附近飞行体质心的方向飞行。如果个体向着群落中心深入的飞行,周围的个体密度会近似的趋于一致。在这种情况下,个体位于邻域的中心,此时群的定心力较小。若有个体在领域的边界上,起相邻的个体就会偏向群落的一边。邻域的质心就会更加的偏向群体,此时对个体定心的冲击力更强,飞行路径就会向着质心偏移。
Real flocks sometimes split apart to go around an obstacle. To be realistic, the simulated flock model must also have this ability. Flock centering correctly allows simulated flocks to bifurcate. As long as an individual boid can stay close to its nearby neighbors, it does not care if the rest of the flock turns away. More simplistic models proposed for flock organization (such as a central force model or a follow the designated leader model) do not allow splits.
真正的鸟群有时会为了绕过障碍而分开。为了更加真实,模拟的鸟群模型也必须具有这种能力。鸟群对中允许模拟鸟群分叉。只要个体能和它的邻居呆在一起,它就不会在意其他的同伴是否转身离开。但是,像更简单的羊群模型就并不会允许群落分割。
.
The flock model presented here is actually a better model of a school or a herd than a flock. Fish in murky water (and land animals with their inability to see past their herdmates) have a limited, short-range perception of their environment. Birds, especially those on the outside of a flock, have excellent long-range “visual perception.” Presumably this allows widely separated flocks to join together. If the flock centering urge was completely localized, when two flocks got a certain distance apart they would ignore each other. Long-range vision seems to play a part in the incredibly rapid propagation of a “maneuver wave” through a flock of birds. It has been shown that the speed of propagation of this wavefront reaches three times the speed implied by the measured startle reaction time of the individual birds. The explanation advanced by Wayne Ports is that the birds perceive the motion of the oncoming “maneuver wave” and time their own turn to match it. Potts refers to this as the “chorus line” hypothesis.
不同的模型对于物体的感知是不同的。羊群,或者在浑水里的鱼群,它们对于视线的感知比较弱,而天空中的鸟群的视线感知是非常惊人的。据推测,这使得广泛分散的鸟群聚集在一起。如果完全定位了羊群的定心冲动,当两个羊群相距一定距离时,它们就会忽略对方。
仲裁独立的行为
The three behavioral urges associated with flocking (and others to be discussed below) each produce an isolated suggestion about which way to steer the boid. These are expressed as acceleration requests. Each behavior says: “if I were in charge, I would accelerate in that direction.” The acceleration request is in terms of a 3D vector that, by system convention, is truncated to unit magnitude or less. Each behavior has several parameters that control its function; one is a “strength,” a fractional value between zero and one that can further attenuate the acceleration request. It is up to the navigation module of the boid brain to collect all relevant acceleration requests and then determine a single behaviorally desired acceleration. It must combine, prioritize, and arbitrate between potentially conflicting urges. The pilot module takes the acceleration desired by the navigation module and passes it to the flight module, which attempts to fly in that direction.
上述的三条原则都产生关于引导个体方向的相对独立的建议。这些都产生了一个加速的请求。通常情况下,会产生三种不同的加速方向的需求。这些加速请求是一个基于3D的矢量,由几个不同的参数来控制。需要一个个体的大脑模块收集所有的加速请求,然后进行整合,将所有的冲突欲望进行整合、排序和权衡。然后向飞行模块输出一个加速度(包括方向和大小),让个体向那个方向飞行。
The easiest way to combine acceleration requests is to average them. Because of the included “strength” factors, this is actually a weighted average. The relative strength of one behavior to another can be defined this way, but it is a precarious interrelationship that is difficult to adjust. An early version of the boid model showed that navigation by simple weighted averaging of acceleration requests works “pretty well.” A bold that chooses its course this way will fly a reasonable course under typical conditions. But in critical situations, such as potential collision with obstacles, conflicts must be resolved in a timely manner. During high-speed flight, hesitation or indecision is the wrong response to a brick wall dead ahead.
组合加速请求的最简单方法是平均它们。由于包含了“强度”因素,这实际上是一个加权平均值。一种行为对另一种行为的相对强度可以这样定义,但这是一种不稳定的相互关系,很难调整。boids模型的一个早期版本显示,通过简单加权平均加速请求的导航不错。选择这种方式的飞机将在典型条件下飞出合理的航线。但在关键情况下,如可能与障碍发生冲突,必须及时解决冲突。在高速飞行中,面对前方的一堵砖墙,犹豫不决是错误的反应。
The main cause of indecision is that each behavior might be shouting advice about which way to turn to avoid disaster, but if those acceleration requests happen to lie in approximately opposite directions, they will largely cancel out under a simple weighted averaging scheme. The boid would make a very small turn and so continue in the same direction, perhaps to crash into the obstacle. Even when the urges do not cancel out, averaging leads to other problems. Consider flying over a gridwork of city streets between the skyscrapers; while “'fly north” or “fly east” might be good ideas, it would be a bad idea to combine them as “fly northeast.”
犹豫不决的主要原因是,每个行为可能都在大声建议转向哪个方向以避免灾难,但如果这些加速请求碰巧位于大约相反的方向,它们将在一个简单的加权平均方案下基本上抵消掉。个体会做一个非常小的转弯,然后继续朝同一个方向前进,这样也许会撞到障碍物。
Techniques from artificial intelligence, such as expert systems, can be used to arbitrate conflicting opinions. However, a less complex approach is taken in the current implementation. Prioritized acceleration allocation is based on a strict priority ordering of all component behaviors, hence of the consideration of their acceleration requests. (This ordering can change to suit dynamic conditions.) The acceleration requests are considered in priority order and added into an accumulator. The magnitude of each request is measured and added into another accumulator. This process continues until the sum of the accumulated magnitudes gets larger than the maximum acceleration value, which is a parameter of each boid. The last acceleration request is trimmed back to compensate for the excess of accumulated magnitude. The point is that a fixed amount of acceleration is under the control of the navigation module; this acceleration is parceled out to satisfy the acceleration request of the various behaviors in order of priority. In an emergency the acceleration would be allocated to satisfy the most pressing needs first; if all available acceleration is “'used up,” the less pressing behaviors might be temporarily unsatisfied. For example, the flock centering urge could be correctly ignored temporarily in favor of a maneuver to avoid a static obstacle.
来自人工智能的技术,例如专家系统就可以很好的解决这一问题。不过,作者当前的模型并没有应用这一技术,而是选择了一个较为简单的实现方法,对于加速度进行优先级排序。加速请求按优先级顺序考虑并添加到累加器中。每个请求的大小被测量并添加到另一个累加器中。这个过程一直持续到累积的幅度的总和大于最大加速度值,最大加速度值是每个个体的一个参数。重点是,一个固定的加速度是在导航模块的控制下;该加速度按优先级顺序进行分配,以满足各种行为对加速度的要求。
模拟的感知
The bold model does not directly simulate the senses used by real animals during flocking (vision and hearing) or schooling (vision and fishes’ unique “lateral line” structure that provides a certain amount of pressure imaging ability [23, 24]). Rather the perception model tries to make available to the behavior model approximately the same information that is available to a real animal as the end result of its perceptual and cognitive processes.
这一部分的功能主要是过滤掉实现Boids软件的多余的可用信息。模拟软件中的信息是可以通过访问描述环境的位置、方向和速度的集合数据库。在自然中,群落中的动物周围的环境对其的感知存在大量的影响,导致它们所能接受的信息十分有限。
This is primarily a matter of filtering out the surplus information that is available to the software that implements the boid’s behavior. Simulated boids have direct access to the geometric database that describes the exact position, orientation, and velocity of all objects in the environment. The real bird’s information about the world is severely limited because it per- ceives through imperfect senses and because its nearby flock- mates hide those farther away. This is even more pronounced in herding animals because they are all constrained to be in the same plane. In fish schools, visual perception of neighboring fish is further limited by the scattering and absorption of light by the sometimes murky water between them. These factors combine to strongly localize the information available to each animal.
如果给每个个体提供完美而全面的信息这显然与现实相悖,并会导致模型的失败。作者认为需要给个体提供有限的数据量。本文推演得到的结果是,完整的群落的聚集运动,始终依赖于个体有限的、局部的世界观。
This is primarily a matter of filtering out the surplus information that is available to the software that implements the boid’s behavior. Simulated boids have direct access to the geometric database that describes the exact position, orientation, and velocity of all objects in the environment. The real bird’s information about the world is severely limited because it per- ceives through imperfect senses and because its nearby flock- mates hide those farther away. This is even more pronounced in herding animals because they are all constrained to be in the same plane. In fish schools, visual perception of neighboring fish is further limited by the scattering and absorption of light by the sometimes murky water between them. These factors combine to strongly localize the information available to each animal.
在鸟群模型的早期版本中,吸引力和排斥力的度量是按距离线性加权的。这样产生的动画效果,与现实中的情景相差甚远。所以作者又将模型改为使用距离的平方反比。这样看起来更加自然。
Boids感知模型非常特别,避免了实际模拟视觉。人工视觉是一个极其复杂的问题,远远超出了这项工作的范围。但如果Boids能够“看到”它们的环境,它们在路径规划方面就会比目前的模型更好。构造简单的迷宫形状是可能的,它会混淆当前的Boid模型,但会很容易地被一个有视觉的Boid解决。
即时群聚
The flocking model described above gives boids an eagerness to participate in an acceptable approximation of flock-like motion. Boids released near one another begin to flock together, cavorting and jostling for position. The boids stay near one another (flock centering) but always maintain prudent separation from their neighbors (collision avoidance), and the flock quickly becomes “polarized”–its members heading in approximately the same direction at approximately the same speed (velocity matching); when they change direction they do it in synchronization. Solitary boids and smaller flocks join to become larger flocks, and in the presence of external obstacles (discussed below), larger flocks can split into smaller flocks.
上述的群体模型中的个体参与着一个群体运动。被释放的个体群聚在一起,相互争抢位置,交错出现在群体的空间中。相互靠近,又彼此远离,群体迅速的因近处邻居的个体更改着速度。小群落可以和其他群落合并成大群落。大群落也可以因为外部障碍的突然出现,进而分割成小群落。
For each simulation run, the initial position (within a specified ellipsoid), heading, velocity, and various other parameters of the boid model are initialized to values randomized within specified distributions. A restartable random-number generator is used to allow repeatability. This randomization is not required; the boids could just as well start out arranged in a regular pattern, all other aspects of the flock model are completely deterministic and repeatable.
对于每次模拟运行,初始位置、航向、速度和boids模型的各种其他参数被初始化为在指定分布内随机化的值。一个可重新启动的随机数生成器被用来允许重复。这种随机化不是必需的;boids可以按照规则的模式开始排列,鸟群模型的所有其他方面都是完全确定的和可重复的。
When the simulation is run, the flock’s first action is a reaction to the initial conditions. If the boids started out too closely crowded together, there is an initial “flash expansion” where the mutual desire to avoid collision drives the boids radially away from the site of the initial over-pressure. If re-leased in a spherical shell with a radius smaller than the “neighborhood” radius, the boids contract toward the sphere’s center; otherwise they begin to coalesce into small flockettes that might themselves begin to join together. If the boids are confined within a certain region, the smaller flocks eventually conglomerate into a single flock if left to wander long enough.
Boids感知模型非常特别,避免了实际模拟视觉。人工视觉是一个极其复杂的问题,远远超出了这项工作的范围。但如果Boids能够“看到”它们的环境,它们在路径规划方面就会比目前的模型更好。构造简单的迷宫形状是可能的,它会混淆当前的Boid模型,但会很容易地被一个有视觉的Boid解决。
脚本运行的群聚
The behaviors discussed so far provide for the ability of individual birds to fly and participate in happy aimless flocking. But to combine flock simulations with other animated action, we need more direct control over the flock. We would like to direct specific action at specific times (for example, “the flock enters from the left at :02.3 seconds into the sequence, turns to fly directly upward at :03.5, and is out of the frame at :04.0”).
为了将鸟群模拟与其他动画动作结合起来,我们需要对鸟群进行更直接的控制。需要在指定的时间点添加指定的动作。
The current implementation of the bold model has several facilities to direct the motion and timing of the flock action. First, the simulations are run under the control of a general-purpose animation scripting system [36]. The details of that scripting system are not relevant here except that, in addition to the typical interactive motion control facilities, it provides the ability to schedule the invocation of user-supplied software (such as the flock model) on a frame-by-frame basis. This scripting facility is the basic tool used to describe the timing of various flock actions. It also allows flexible control over the time-varying values of parameters, which can be passed down to the simulation software. Finally the script is used to set up and animate all nonbehavioral aspects of the scene, such as backgrounds, lighting, camera motion, and other visible objects.
目前Boids模型有几个设定,来控制运动同时间的关系。首先,模拟是在一个通用动画脚本系统的控制下运行的。除了典型的交互式运动控制设施外,脚本系统还提供了一帧一帧地调度用户提供的软件调用的能力,除此之外,脚本系统的细节在这里并不相关。这个脚本工具是用来描述各种群集操作的时间的基本工具。
The primary tool for scripting the flock’s path is the migratory urge built into the boid model. In the current model this urge is specified in terms of a global target, either as a global direction (as in “going Z for the winter”) or as a global position–a target point toward which all birds fly. The model computes a bounded acceleration that incrementally turns the boid toward its migratory target.
编写鸟群路径脚本的主要工具是内置在boids模型中的迁徙冲动。在当前的模型中,这种冲动是通过一个全局目标来指定的,要么是一个全局方向,要么是一个全局位置——所有鸟类都飞向的目标点。该模型计算一个有界加速度,使boids逐渐转向它的迁移目标。
We can lead the flock around by animating the goal point along the desired path, somewhat ahead of the flock. Even if the migratory goal point is changed abruptly the path of each boid still is relatively smooth because of the flight model’s simulated conservation of momentum. This means that the boid’s own flight dynamics implement a form of smoothing interpolation between “control points.”
使用脚本系统,我们可以动画一个动态参数,其值是一个全局位置向量或全局方向向量。这个参数可以传递给鸟群,鸟群可以将它传递给所有的boids,每个boids设置自己的“迁移目标寄存器”。因此,所有鸟类的全球迁徙行为都可以从脚本中直接控制。
由于飞行模型的模拟动量守恒,即使移动目标点突然改变,个体的路径仍然相对光滑。这意味着Boids自身的飞行动力学实现了“控制点”之间的平滑插值形式。
避免环境障碍
The most interesting motion of a simulated flock comes from interaction with other objects in the environment. The isolated behavior of a flock tends to reach a steady state and becomes rather sterile. The flock can be seen as a relaxation solution to the constraints implied by its behaviors. For example, the conflicting urges of flock centering and collision avoidance do not lead to constant back and forth motion, but rather the boids eventually strike a balance between the two urges (the degree of damping controls how soon this balance is reached). Environmental obstacles and the boid’s attempts to navigate around them increase the apparent complexity of the behavior of the flock. (In fact the complexity of real flocks might be due largely to the complexity of the natural environment.)
模拟鸟群最有趣的运动来自于与环境中其他物体的相互作用。群体的孤立行为往往会达到稳定状态。集中注意力和避免碰撞这两种相互冲突的冲动不会导致持续的前后运动,但boids最终会在这两种冲动之间取得平衡。环境障碍和boid试图绕过它们的尝试增加了鸟群行为的明显复杂性
Environmental obstacles are also important from the standpoint of modeling the scene in which we wish to place the flock. If the flock is scripted to fly under a bridge and around a tree, we must be able to represent the geometric shape and dimension of these obstacles. The approach taken here is to independently model the “shape for rendering” and the “shape for collision avoidance.” The types of shapes currently used for environmental obstacles are much less complicated than the models used for rendering of computer graphic models. The current work implements two types of shapes of environmental collision avoidance. One is based on the force field concept, which works in undemanding situations but has some shortcomings. The other model called steer-to-avoid is more robust and seems closer in spirit to the natural mechanism.
加粗的分别是两种不同的模型名
从我们希望放置鸟群的场景建模的角度来看,环境障碍也很重要。如果鸟群在桥下和树下飞行,我们必须能够表示这些障碍的几何形状和尺寸。这里采用的方法是独立建模“渲染形状”和“避免碰撞形状”。目前实现了两种不同的方法避障,一种是基于力场的模型,它适用于要求不高的情况,但也有一些缺点。另一种被称为“转向-规避”(steer-to-avoid)的模型鲁棒性更强,也更接近自然机制。
下面分别介绍这两种避障机制。
The force field model postulates a field of repulsion force emanating from the obstacle out into space; the boids are increasingly repulsed as they get closer to the obstacle. This scheme is easy to model; the geometry of the field is usually fairly simple and so an avoidance acceleration can be directly calculated from the field equation. These models can produce good results, such as in “Eurythmy” [4], but they also have drawbacks that are apparent on close examination. If a boid approaches an obstacle surrounded by a force field at an angle such that it is exactly opposite to the direction of the force field, the boid will not turn away. In this case the force field serves only to slow the boid by accelerating it backwards and provides no side thrust at all. The worst reaction to an impending collision is to fail to turn. Force fields also cause problems with “peripheral vision” The boid should notice and turn away from a wall as it flies toward it, but the wall should be ignored if the boid is flying alongside it. Finally, force fields tend to be too strong close up and too weak far away; avoiding an obstacle should involve long-range planning rather than panicky corrections at the last minute.
力场模型假设一个斥力场从障碍物发射到空间;当个体靠近障碍物时,它们会受到越来越多的排斥。该方案易于建模;场的几何形状通常是相当简单的,因此可以直接从场方程计算避避加速度。
Steer-to-avoid is a better simulation of a natural bird guided by vision. The boid considers only obstacles directly in front of it. (It finds the intersection, if any, of its local Z axis with the obstacle.) Working in local perspective space, it finds the silhouette edge of the obstacle closest to the point of eventual impact. A radial vector is computed which will aim the boid at a point one body length beyond that silhouette edge (see figure 2). Currently steer-to-avoid has been implemented for several obstacle shapes: spheres, cylinders, planes, and boxes. Collision avoidance for arbitrary convex polyhedral obstacles is being developed.
“转向-避开”模型更好地模拟了由视觉引导的自然鸟类。个体只考虑前面的障碍。在局部透视空间中,它找到了最接近最终冲击点的障碍物的轮廓边缘。它会计算一个径向矢量,它将把加速度指向轮廓边缘以外的一点。
Obstacles are not necessarily fixed in space; they can be animated around by the script during the animation. Or more interestingly, the obstacles can be behavioral characters. Sparrows might flock around a group of obstacles that is in fact a herd of elephants. Similarly, behavioral obstacles might not merely be in the way; they might be objects of fear such as predators. It has been noted that natural flocking instincts seem to be sharpened by predators.
障碍不一定固定在空间中;它们可以在动画过程中被脚本动画化。更有趣的是,障碍可以是行为角色。麻雀可能会聚集在一群障碍物周围,而这些障碍物实际上是一群大象。同样,行为障碍可能不仅仅是障碍;它们可能是像捕食者一样的恐惧对象。我们自然的发现,自然的群聚本能被掠食者强化了。
Boids模型的其他应用
这里作者介绍了一些Boids在其他方面的应用。在模拟自然界动物群落的群聚运动之外,也可以模拟公路上的汽车运动,甚至是宇宙飞船在太空的航行(如果过于密集的话)。
更重要的应用是,帮助那些自然社会学家做调研,通过模拟的方式可以观察到特定的运动,也许这些运动在自然界中要等上很久。
算法分析
Boids模型的算法时间复杂度是O(N^2)。因为每一个个体都需对其他个体进行遍历,随着个体数量的增加,复杂度也会增加。
如前所述,真正的鸟类可能对整个鸟群的数量没有那么敏感。问题的一部分是我们试图在一台计算机上运行整个鸟群的模拟。自然的解决方案是使用分布式处理,就像真正的鸟群那样。如果我们对每个个体使用单独的处理器,那么即使是简单的群集算法的实现也将是O(N)。但是这仍意味着复杂度会随着个体数量的增加而增加。
我们想要得到一个O(1)的算法,因为自然中便是如此,鸟群中的个体对总体数量并不敏感。因为只有总体数量较小的时候,这样是可行的。
目前有两种方法进行优化。
一个是群体的动态空间分割;根据它们在空间中的位置,个体被分类成一个“箱子”格子。个体可以通过检查其当前位置附近的“桶”快速接近周围的鸟群伙伴。
另一种方法是进行增量碰撞检测。一般的碰撞检测是另一个O(N)算法,但如果一个增量地碰撞检测,基于一个部分解决方案,描述了形势稍等,然后算法需要只担心变化可以运行更快,假设增量变化很小。
运行环境
编写/运行环境如下:
flock软件编写:Symbolics Common Lisp
动画制作:Symbolics 3600 Lisp Machine
flock软件实现:Symbolics Common Lisp
系统几何分层构建:S-Geometry
Boids软件没有为提升速度进行优化。
Symbolics Common的产品如下图:

真的是上古神机
将来的工作
This paper has largely ignored the internal animation of the geometrical model that provides the visual representation of the bold. The original motion tests produced with these models all show flocks of little abstract rigid shapes that might be paper airplanes. There was no flapping of wings nor turning of heads, and there was certainly no character animation. These topics are all important and pertinent to believable animation of simulated flocks. But the underlying abstract nature of flocking as polarized, noncolliding aggregate motion is largely independent of these issues of internal shape change and articulation. This notion is supported by the fact that most viewers of these simulations identify the motion of these abstract objects as “flocking’” even in the absence of any internal animation.
本文在很大程度上忽略了几何模型的内部动画,而几何模型提供了粗体的视觉表现。这些主题都是重要的,并且与真实的模拟鸟群动画相关。作者希望可以通过动画更真实而细腻的反应Boids飞行的过程。
But doing a believable job of melding these two aspects of the motion is more than a matter of concatenating the action of an internal animation cycle for the character with the motion defined by geometrical flight. There are important issues of synchronization between the current state of the flight dynamics model, and the amplitude and frequency of the wing motion cycle. Topics of current development include internal animation, synchronization, and interfaces between the simulation-based flock model and other more traditional, interactive animation scripting systems. We would like to allow a skilled computer animator to design a bird character and define its “wing flap cycle” using standard interactive modeling and scripting techniques, and then be able to take this cyclic motion and “plug it in” to the flock simulation model causing the boids in the flock to fly according to the scripted cycle.
同时所讨论的行为都是简单的、孤立的、低复杂度的行为。boids模型具有几何和运动状态,但没有显著的心理状态。真实的动物有着比简单的避免痛苦碰撞的愿望更复杂、抽象的行为;他们有更复杂的动机,而不仅仅是想要飞到太空中的某个点。更有趣的行为模型将考虑饥饿、寻找食物、对捕食者的恐惧、周期性的睡眠需求等等。如果应用自然社会学领域,这些因素也是需要考虑在内的。
结论
This paper has presented a model of polarized, noncolliding aggregate motion, such as that of flocks, herds, and schools. The model is based on simulating the behavior of each bird independently. Working independently, the birds try both to stick together and avoid collisions with one another and with other objects in their environment. The animations showing simulated flocks built from this model seem to correspond to the observer’s intuitive notion of what constitutes “flock-like motion.” However it is difficult to objectively measure how valid these simulations are. By comparing behavioral aspects of the simulated flock with those of natural flocks, we are able improve and refine the model. But having approached a certain level of realism in the model, the parameters of the simulated flock can be altered at will by the animator to achieve many variations on flock-like behavior.
本文提出了一个极化的、非碰撞的集合体运动模型,如群、群和群的运动模型。该模型是在独立模拟每只鸟行为的基础上建立的。
它们各自独立工作,同时努力粘在一起,避免与彼此以及环境中的其他物体发生碰撞。动画显示了由这个模型构建的模拟鸟群,似乎符合观察者对“类鸟群运动”的直观概念。然而,很难客观地衡量这些模拟的有效性。
通过对模拟羊群和自然羊群行为方面的比较,我们可以改进和完善模型。但是,在模型接近一定程度的现实主义后,模拟鸟群的参数可以由动画师随意更改,以实现许多鸟群行为的变体。
终于搞完啦,完结撒花❀~~