神经网络Matlab的直接使用

拟合和预测

网上看了这么多关于神经网络的文件，又是什么BT神经的，又是什么模糊神经的，对我而言统统毫无意义。
本人身为土木工科生，思想就是，能用到的就是好的，能解决问题的钢筋就是可以盖大楼的东西。
Matlab里面已经提供了神经网络的函数工具箱。
对我这个专业或者数学建模比赛而言，它目前能起到的就是一个函数较优秀的拟合的作用，而且我并不需要在意拟合出来的是几次方程。
或者，也可以起到一点评估过去或者未来的作用

代码

这是我已经放进去的3种神经网络的m文件

function [net,tr] = shenjin(choice,P,T)
net=newff(minmax(P),[20,1],... % 隐单元的神经元数 20，输出 1，可调
{'tansig','purelin'});
if(choice==1)
    %  采用 L-M 优化算法 TRAINLM
    net.trainFcn='trainlm';
    %  设置训练参数
    net.trainParam.epochs = 500;
    net.trainParam.goal = 1e-6;
    net=init(net);
    %  重新初始化
elseif(choice==2)
    %  采用贝叶斯正则化算法 TRAINBR
    net.trainFcn='trainbr';
    %  设置训练参数
    net.trainParam.epochs = 500;
    randn('seed',192736547);
    net = init(net);
    %  重新初始化
elseif(choice==3)
    %  采用动量梯度下降算法 TRAINGDM
    %  当前输入层权值和阈值
    inputWeights=net.IW{1,1};
    inputbias=net.b{1};
    %  当前网络层权值和阈值
    layerWeights=net.LW{2,1};
    layerbias=net.b{2};
    %  设置训练参数
    net.trainParam.show = 50;
    net.trainParam.lr = 0.05;
    net.trainParam.mc = 0.9;
    net.trainParam.epochs = 1000;
    net.trainParam.goal = 1e-3;
end
%  调用相应算法训练 BP 网络
[net,tr]=train(net,P,T);
end

然后配合main文件使用

% L-M 优化算法（trainlm）和贝叶斯正则化算法（trainbr），用以训练 BP 网络
% 使其能够拟合某一附加有白噪声的正弦样本数据，渡边笔记
% 神经网络的初始和常数设置，请在shenjin.m修改
clc,clear;close all;

% 0.全选，如果数据不多时可以操作
% 1.L-M 优化算法 TRAINLM
% 2.贝叶斯正则化算法 TRAINBR
% 3.动量梯度下降算法 TRAINGDM
% trainbfg---BFGS算法（拟牛顿反向传播算法）训练函数；
% trainbr---贝叶斯归一化法训练函数；
% traincgb---Powell-Beale共轭梯度反向传播算法训练函数；
% traincgp---Polak-Ribiere变梯度反向传播算法训练函数；
% traingd---梯度下降反向传播算法训练函数；
% traingda---自适应调整学习率的梯度下降反向传播算法训练函数；
% traingdm---附加动量因子的梯度下降反向传播算法训练函数；
% traingdx---自适应调整学习率并附加动量因子的梯度下降反向传播算法训练函数；
% trainlm---Levenberg-Marquardt反向传播算法训练函数；
% trainoss---OSS（one step secant）反向传播算法训练函数；
% trainrp---RPROP（弹性BP算法）反向传播算法训练函数；
% trainscg---SCG（scaled conjugate gradient）反向传播算法训练函数；
% trainb---以权值/阈值的学习规则采用批处理的方式进行训练的函数；
% trainc---以学习函数依次对输入样本进行训练的函数；
% trainr---以学习函数随机对输入样本进行训练的函数。
% 当调用train函数时，上述训练函数被用于训练网络
L = 3; %共有三种方法,我觉得够用了
choice = 0;

% P 为输入矢量
P = [-1:0.05:1];
% T 为目标矢量
T = sin(2*pi*P)+0.1*randn(size(P));

%  绘制样本数据点
% 3种全选，比较谁更合适
% choice = 0
if choice == 0
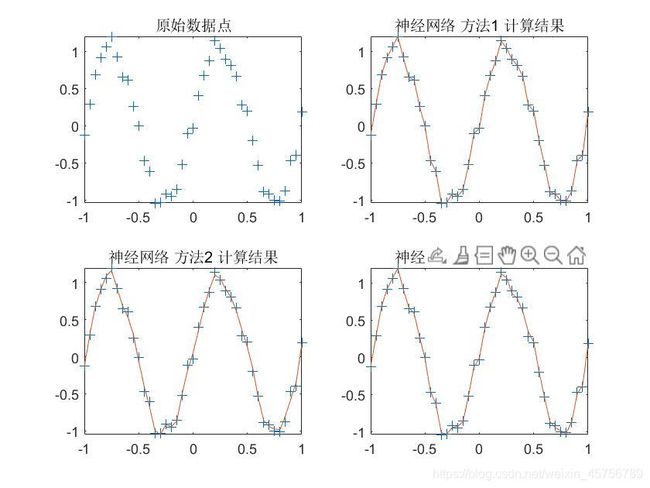
    subplot(2,2,1)
    plot(P,T,'+');
    title('原始数据点');
    for i = 1:L
        % 神经网络
        [net,tr] = shenjin(i,P,T);
        %  对 BP 网络进行仿真
        A = sim(net,P);
        subplot(2,2,i+1)
        plot(P,T,'+',P,A);
        title(['神经网络 方法',num2str(i),' 计算结果']);
        %  计算仿真误差
        E = T - A;
        MSE(i) = mse(E); % mse 函数用于计算均方误差
        % 均方误差（mean-square error, MSE）是反映估计量与被估计量之间差异程度的一种度量
    end
    for i = 1:L
        disp(['神经网络 方法',num2str(i),' 的_均方误差_为 : ',num2str(MSE(i))])
    end
    [~,Min] = min(MSE);
    disp(['神经网络 方法',num2str(Min),' 比较优'])
else
    subplot(1,2,1)
    plot(P,T,'+');
    title('原始数据点');
    % 神经网络
    [net,tr] = shenjin(i,P,T);
    % 对 BP 网络进行仿真
    A = sim(net,P);
    subplot(1,2,2)
    plot(P,T,'+',P,A);
    title(['神经网络 方法',num2str(choice),' 计算结果']);
    %  计算仿真误差
    E = T - A;
    MSE = mse(E); % mse 函数用于计算均方误差
    % 均方误差（mean-square error, MSE）是反映估计量与被估计量之间差异程度的一种度量
    disp(['神经网络 方法',num2str(choice),' 的_均方误差_为 : ',num2str(MSE)])
end

% 这个用于分析是否可以很好的进行线性回归
% [m,b,r] = postreg(A, P);

% 神经网络的简单使用方法
% [Y] = sim(net,P);
% 输入即可输出，维度应与元数据保存一致

输入和输出

结果如下


我写代码注释都很详细的，无需多言，以上。
有什么错误的地方，欢迎指正，相互交流，谢谢。