【人工智能】Fisher 线性分类器的设计与实现（QDU）

• 【人工智能】Astar算法求解8数码问题（QDU）
  
• 【人工智能】利用α-β搜索的博弈树算法编写一字棋游戏（QDU）
  
• 【人工智能】Fisher 线性分类器的设计与实现（QDU）
• 【人工智能】感知器算法的设计实现（QDU）
• 【人工智能】SVM 分类器的设计与应用（QDU）
• 卷积神经网络 CNN 框架的实现与应用（写的比较水，就没放上）

当时比较憨，不知sklearn中有数据增强的函数，还自己实现了一下，完全没必要。

实验目的

1. 掌握 Fisher 线性判别的基本原理
2. 利用 Fisher 线性判别解决基本的两类线性分类问题

实验原理

基本思想

FDA是一种监督学习的降维技术，以二维数据集的二分类为例（通俗点讲二维数据集就是平面直角坐标系中的散点，二分类就是这些数据集要么是第一类，要么是第二类），有很多种方法对这些点进行分类，比如我们可以找一条直线去分隔两类点，线左边的是第一类，线右边的是第二类等等方法。而线性判别要做的是找一条直线，让这些散点都投影到该直线上，让同一类的点尽可能在直线上分布地近点，而不同类的点在直线上分布尽可能地远点。

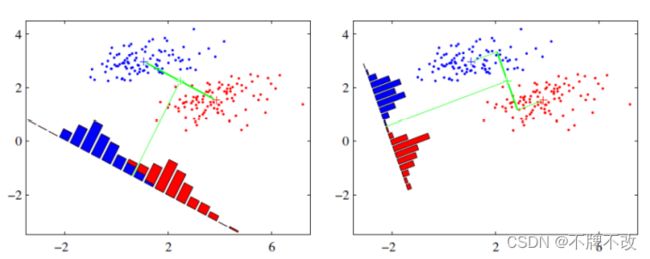
可能还是有点抽象，我们先看看最简单的情况。假设我们有两类数据 分别为红色和蓝色，如下图所示，这些数据特征是二维的，我们希望将这些数据投影到一维的一条直线，让每一种类别数据的投影点尽可能的接近，而红色和蓝色数据中心之间的距离尽可能的大。

上图提供了两种投影方式，哪一种能更好的满足我们的标准呢？从直观上可以看出，右图要比左图的投影效果好，因为右图的红色数据和蓝色数据各个较为集中，且类别之间的距离明显。左图则在边界处数据混杂。

在实际应用中，散点类别的确定往往不能仅由两种特征来确定，这就需要将FDA扩展到高维了。对于高维而言也是类似的，无非就是要去确定一个超平面，使得高维坐标系中的点投影到该超平面上同一类点尽可能近，不同类点尽可能远。降维就是FDA的主要思想。

判别函数

线性判别函数需要确定$W$和$w_0$可以用于判断某个样本$X$所在的类

判别函数：$g(X)=W^{T}X+w_0$

其中，$X$为样本的特征（即样本点在高维坐标系下的坐标）；$W$为权向量（即待求参数），$w_0$为阈值权，是个常数。

在二分类中，判别函数的意义在于确定一个决策面（决策面就是用于分隔每类散点的超平面），决策面的一侧为第一类点，另一侧为第二类点，在面上的点我们可以将该点归为第一类也可以归为第二类，也可以选择不对这些点分类。根据其意义，可以总结出判别规则：
$$\{\begin{array}{l}ifg(X)>0,thenX\in clas{s}_1\\ ifg(X)<0,thenX\in clas{s}_2\\ ifg(X)=0,thenX\in clas{s}_{1}orclas{s}_2\end{array}$$
那么，$g(X)=0$就是对应的决策面方程，即$W^{T}X+w_0=0$

准则函数

准则函数是用于获取最佳$W$的函数，通过下面的讲解会发现准则函数是用于确定投影方向的函数

以FDA“同近异远”的主要思想为目标定义Fisher准则函数，当准则函数的值尽可能地大（或者小）时可以使两类尽量分开，同类尽量聚集。也就是说我们要将分类的好坏程度量化，用于量化的函数就是Fisher准则函数（可以理解为损失函数），当其值取最大（或最小）时得到的参数值就是我们的目标参数值，也就是决策面。

---

获取投影方向$W$

以二分类为例。

将$X$空间中的$N$个具有$d$个特征（即$d$维）的样本点$x_1$，$x_2$，$...$，$x_N$通过一个$d$维向量$w$投影到一维$Y$空间中，其中$N_1$个属于$w_1$类的样本记为子集${\Gamma }_1$，$N_2$个属于$w_2$类的样本记为子集${\Gamma }_2$。投影到一维$Y$空间中，对应为$y_i=W^T{x}_i$，$i=1,2,...,N$。

基本参量：

在$d$维$X$空间中，

• 各类样本的均值向量$m_i$
  $$m_i=\frac{1}{N_i}\sum _{x\in {\Gamma }_i}x,i=1,2$$

• 样本类内离散度矩阵$S_i$
  $$S_i=\sum _{x\in {\Gamma }_i}(x-m_i)(x-m_i{)}^T,i=1,2$$

  $S_i$为对称阵

• 总样本类内离散度矩阵$S_w$
  $$S_w=S_1+S_2$$

• 样本类间离散度矩阵$S_b$
  $$S_b=(m_1-m_2)(m_1-m_2{)}^T$$

  $S_b$为对称阵

在一维$Y$空间中，

• 各类样本的均值$\widetilde{m_i}$
  $$\widetilde{m_i}=\frac{1}{N_i}\sum _{x_j\in {\Gamma }_i}{y}_j,i=1,2$$

  为了表示方便，$\widetilde{m_i}$式中的$x_j$和$y_j$将简写为$x$和$y$，含义不变，$y$为$x$对应的投影值

• 样本类内离散度$\widetilde{S_i^2}$
  $$\widetilde{S_i^2}=\sum x\in {\Gamma }_i(y-\widetilde{m_i}{)}^2,i=1,2$$

• 总样本类内离散度$\widetilde{S_w}$
  $$\widetilde{S_w}=\widetilde{S_1^2}+\widetilde{S_2^2}$$

• 总样本类间散度$\widetilde{S_b^2}$
  $$\widetilde{S_b^2}=(\widetilde{m_1}-\widetilde{m_2}{)}^2$$

Fisher准则函数定义为：
$$max{J}_F(W)=\frac{(\widetilde{m_1}-\widetilde{m_2}{)}^2}{\widetilde{S_1^2}+\widetilde{S_2^2}}$$

表示的含义即为“同近异远”

由各类样本的均值可推出：
$$\widetilde{m_i}=\frac{1}{N_i}\sum _{x\in {\Gamma }_i}y=\frac{1}{N_i}\sum _{x\in {\Gamma }_i}{W}^{T}x=W^T(\frac{1}{N_i}\sum _{x\in {\Gamma }_i}x)=W^T{m}_i$$
这样，Fisher准则函数$J_F(W)$的分子可写成：
$$\begin{gathered} (\widetilde{m_1}-\widetilde{m_2}{)}^2 \\ =(W^T{m}_1-W^T{m}_2{)}^2 \\ =(W^T{m}_1-W^T{m}_2)(W^T{m}_1-W^T{m}_2{)}^T \\ =W^T(m_1-m_2)(m_1-m_2{)}^{T}W \\ =W^T{S}_{b}W \end{gathered}$$
现在再来考察$J_F(w)$的分母与$W$的关系：
$$\begin{gathered} \widetilde{S_i^2}=\sum _{x\in {\Gamma }_i}(y-\widetilde{m_i}{)}^2 \\ =\sum _{x\in {\Gamma }_i}(W^{T}x-W^T{m}_i{)}^2 \\ =W^T[\sum _{x\in {\Gamma }_i}(x-m_i)(x-m_i{)}^T]W \\ {W}^T{S}_{w}W \end{gathered}$$
因此，
$$\widetilde{S_1^2}+\widetilde{S_2^2}=W^T(S_1+S_2)W=W^T{S}_{w}W$$
将上述各式代入$J_F(w)$，可得：
$$J_F(w)=\frac{W^T{S}_{b}W}{W^T{S}_{w}W}$$
最佳变换向量$W^{\ast }$的求取：

为求使$J_F(w)=\frac{W^T{S}_{b}W}{W^T{S}_{w}W}$取极大值时的$w^{\ast }$，可以采用Lagrange乘数法求解。令分母等于非零常数，即：
$$W^T{S}_{w}W=c\ne 0$$
定义Lagrange函数为：
$$L(W,\lambda )=W^T{S}_{b}W-\lambda (W^T{S}_{w}W-c)$$
其中$\lambda$为Lagrange乘子。将上式对$W$求偏导数，可得：
$$\frac{\partial L(W,\lambda )}{\partial w}=S_{b}W-\lambda S_{w}W$$
令偏导数为零，则有：
$$\begin{gathered} S_b{W}^{\ast }-\lambda S_w{W}^{\ast }=0 \\ {S}_b{W}^{\ast }=\lambda S_w{W}^{\ast } \end{gathered}$$
其中$W^{\ast }$就是$J_F(W)$的极值解。因为$S_w$非奇异，将上式两边左乘$S_W^{-1}$，可得：
$$S_w^{-1}{S}_b{W}^{\ast }=\lambda W^{\ast }$$
上式为求一般矩阵$S_w^{-1}{S}_b$的特征值问题。利用$S_b=(m_1-m_2)(m_1-m_2{)}^T$的定义，将上式左边的$S_b{W}^{\ast }$写成：
$$S_b{W}^{\ast }=(m_1-m_2)(m_1-m_2{)}^T{W}^{\ast }=(m_1-m_2)R$$
其中$R=(m_1-m_2{)}^T{W}^{\ast }$为标量，所以$S_b{W}^{\ast }$总在向量$(m_1-m_2)$的方向上。因此$\lambda W^{\ast }$可写成：
$$\lambda W^{\ast }=S_w^{-1}(S_b{W}^{\ast })=S_w^{-1}(m_1-m_2)R$$
从而可得：
$$W^{\ast }=\frac{R}{\lambda }{S}_w^{-1}(m_1-m_2)$$
由于我们的目的是寻找最佳的投影方向，$W^{\ast }$的比例因子对此并无影响，因此可忽略比例因子$\frac{R}{\lambda }$，有：
$$W^{\ast }=S_w^{-1}(m_1-m_2)$$
$W^{\ast }$是使Fisher准则函数$J_F(W)$取极大值时的解，也就是$d$维$X$空间到一维$Y$空间的最佳投影方向。

获取阈值$w_0$

有了$W^{\ast }$，就可以把$d$维样本$x$投影到一维，这实际上是多维空间到一维空间的一种映射，这个一维空间的方向$W^{\ast }$相对于Fisher准则函数$J_F(W)$是最好的。利用Fisher准则确定$W$后，就可以将$d$维分类问题转化为一维分类问题，然后，只要确定一个阈值$w_0$即可。

阈值$w_0$的选取：

1. $d$和$N$很大时，$y$近似正态分布，可在Y空间内用贝叶斯分类器

2. 经验，如：

   $w_0=-\frac{1}{2}(\widetilde{m_1}+\widetilde{m_2})$

   $w_0=-\tilde{m}$

   $w_0=-\frac{1}{2}(\widetilde{m_1}+\widetilde{m_2})-\frac{1}{N_1+N_2-2}ln\frac{P(w_1)}{P(w_2)}$

3. 在实际工作中还可以对$w_0$进行逐次修正的方式，选择不同的$w_0$值，计算其对训练样本集的错误率，找到错误率较小的$w_0$值

实验内容

实验一

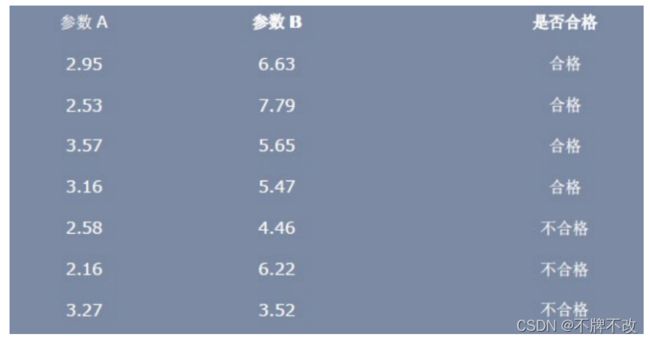
利用 LDA 进行一个分类的问题：假设一个产品有两个参数柔软性 A 和钢性 B来衡量它是否合格，如下图所示：

根据上图，我们可以把样本分为两类，一类是合格的产品，一类是不合格的产品。通过 LDA 算法对训练样本的投影获得判别函数，然后判断测试样本的类别，即输入一个样本的参数，判断该产品是否合格。

实验设计

核心算法就是上面的定义及推导过程；

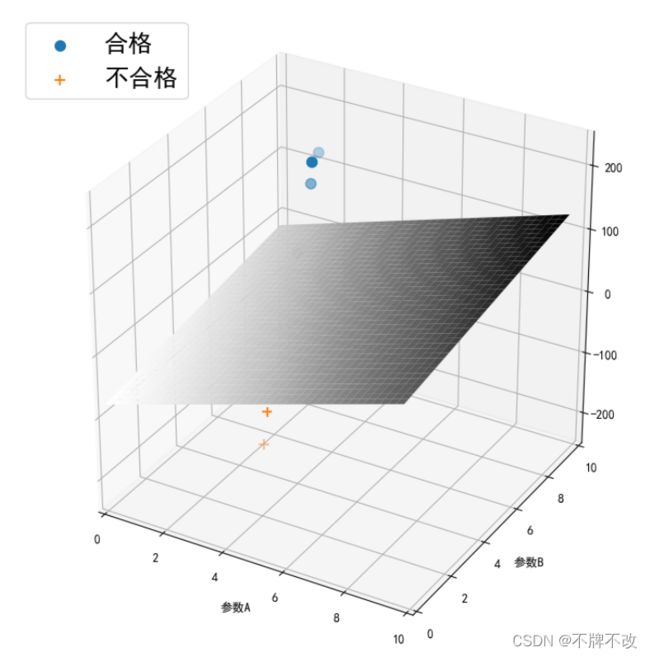
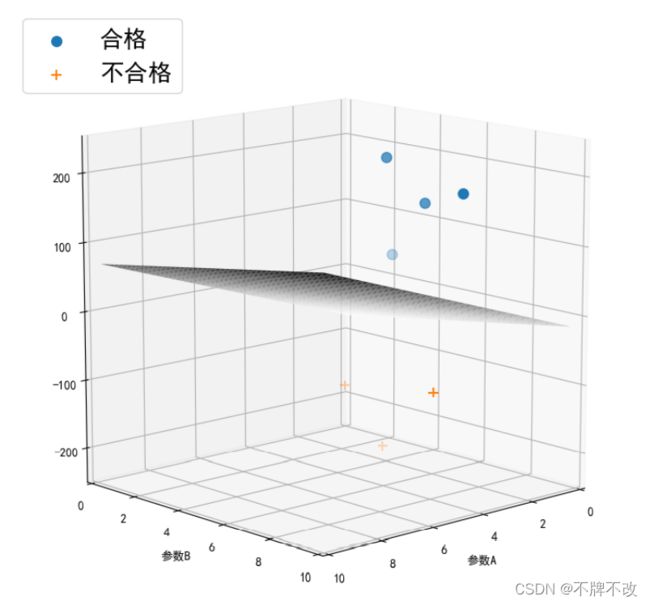
对于给定的数据集（7个样本）进行分类并可视化于空间坐标系中如下：（多角度显示）

由于直接将计算得到的估值作为纵坐标的值会使得散点过度靠近决策面，导致观察不清楚，所以我将得到的估值乘上了一个倍数再进行的可视化

输出$w$向量和阈值$b$：

[14.79808165  6.15861429] 
-76.5777744038943

输出合格样本（4个）得到的判别函数值和不合格样本（3个）的判别函数值：

[7.908179218783431, 8.836977507881159, 11.047547831774295, 3.8717837839741094]
[-10.93130400733638, -6.3073371421071585, -6.509725107366222]

对于训练集样本分类的效果比较好，但是没有测试集，所以仅对训练集样本的判别函数值进行了输出显示和可视化。

实验二

基于 ORL 人脸库，采用LDA的方法对前两个人进行二分类。

数据集简介

• ORL数据库共有400幅人脸图像(40人， 每人10幅， 大小为112像素×92像素)
• 这个数据库比较规范， 大多数图像的光照方向和强度都差不多．
• 但有少许表情、姿势、伸缩的变化， 眼睛对得不是很准， 尺度差异在10%左右。
• 并不是每个人都有所有的这些变化的图像，即有些人姿势变化多一点，有些人表情变化多一点， 有些还戴有眼镜， 但这些变化都不大

正是基于ORL人脸库图像在光照， 以及关键点如眼睛、嘴巴的位置等方面比较统一的特点， 实验可以在该图片集上直接展开， 而不是必须要进行归一化和校准等工作。

说明： .PGM文件可以使用PS打开

第一步：扩充数据集

ORL库样本数太少，所以需要先扩充数据集。

采用Matlab对图像进行处理，包括图像整体亮暗的调整、左右镜像操作、左右移动10像素、顺逆时针旋转10°。经过这些操作，每张图片可以得到七张变换后的图片，再将原图复制一份作为样本集，即一张图片扩充为九张图片，包括经图像处理得到的七张图片和两张原图，因此一个人的图像总共10×9张，两个人总共180张图片。如此，便将数据集扩充到180张。

扩充后，第一个人的第一个照片的九张图：

第二步：图片数据化

通过Matlab将前两个人的总共180张照片变形得到180行10304列的数据，每张照片大小为112×92，所以总共10304列。将矩阵导出为xlsx文件，方便在python中进行数据处理。

第三步：PCA降维

每张照片的每个像素都是一个特征，所以每个样本有10304个特征，而很多特征是具有相关性的，所以我们可以忽略某些特征，只关注对结果影响明显的特征，所以可以采用PCA进行降维处理。

PCA降维的过程：

1. 数据的标准化处理——去均值
2. 计算协方差矩阵
3. 计算特征向量与特征值
4. 根据特征值的大小，选择前k个特征向量组成一个新的特征矩阵
5. 原始数据与新的特征矩阵相乘

机器学习sklearn库直接为我们提供了PCA模块，我们可直接调用该模块对原始数据进行处理，更加简单方便。

大致思路：

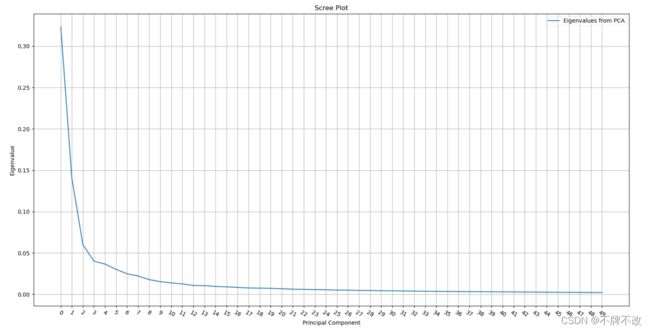
将大小为180的数据集按9：1划分训练集和测试集，先进行一次PCA将10304个特征降维到50个特征：

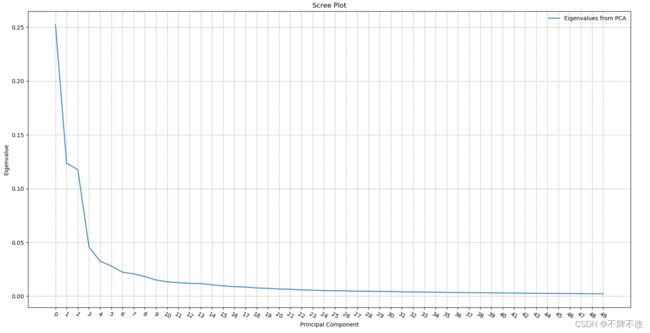
观察前50个特征可以发现，前3个特征起到主导作用，后续变化平缓，所以我将前3个特征作为主成分。

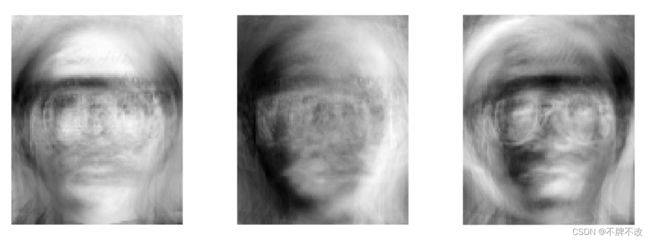
用162个样本降维得到主成分分量矩阵（10304×3），对主成分特征进行可视化：

原数据集与主成分分量矩阵相乘即可实现对数据集进行降维，降维后的数据集矩阵大小为180×3。

第四步：得到LDA判别函数

将降维后的训练集送至“实验一”中的LDA二分类函数中可以得到对应的投影方向$w$和阈值$b$，使用得到的判别函数处理测试集得到每个样本对应的标签，大致情况如下（多次训练可能结果不一样）：

测试集真实标签：[1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0]
测试集预测标签：[1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1]

第五步：评价模型效果

主要采用分析准确率、精确率、召回率、F1-score和观察混淆矩阵的方式评估模型的效果。

交叉报告如下：

              precision    recall  f1-score   support

          p1       1.00      0.86      0.92         7
          p2       0.92      1.00      0.96        11

    accuracy                           0.94        18
   macro avg       0.96      0.93      0.94        18
weighted avg       0.95      0.94      0.94        18

精确率、召回率、F1-score均在85%以上，说明模型效果比较好。

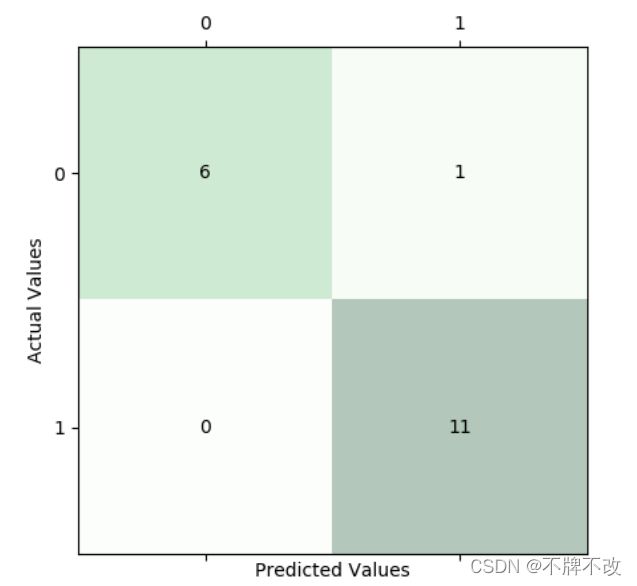
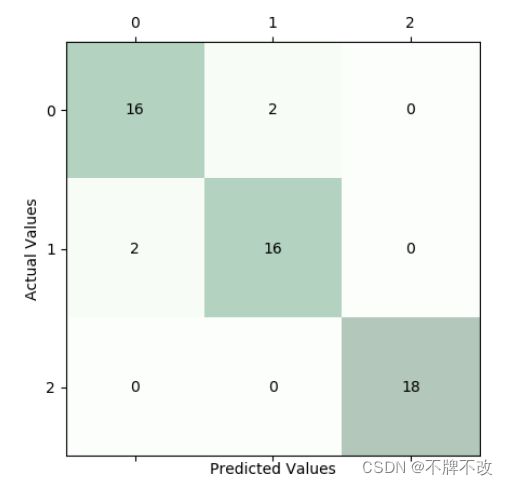
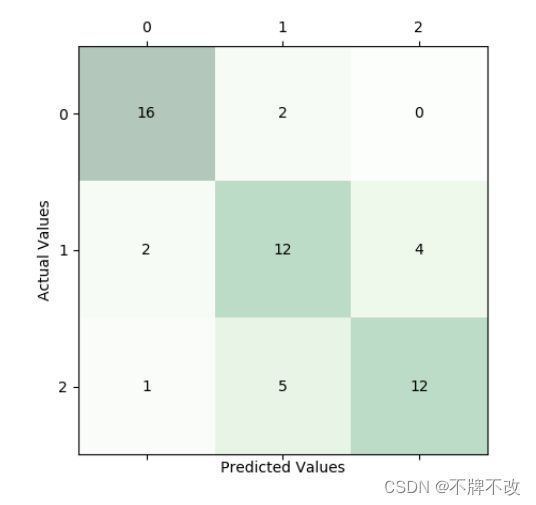
混淆矩阵如下：

混淆矩阵说明将第一个人分类到第二个人的次数为1，其余六次均正确分类，第二个人均未分错。

综上，可见模型比较符合预期。

实验三

多分类问题

对于多类问题，模式有$w_1$，$w_2$，$...$，$w_m$个类别。可分三种情况：

1. 绝对可分（一对多，one-vs-rest, one-over-all）
2. 成对可分
3. 最大值判决（直接多类分类）

第一种情况：绝对可分

每一模式类与其它模式类间可用单个判别平面把一个类分开，$c$类转化为$c$个两类问题，$w_i$与非$w_i$

简单来说，就是先将$w_1$的样本作为一组，$w_2$，$...$，$w_m$的样本作为另一组，根据这两组画一条线将两组分隔；再将$w_2$的样本作为一组，$w_1$，$w_3$，$...$，$w_m$的样本作为另一组根据这两组再画一条线将两组分隔，以此类推。

缺点：

1. 训练样本不均衡而导致分类面有偏（假设多类中各类的训练样本数相当）
2. 出现歧义区域，不会恰好得到c个区域（往往过多）

第二种情况：成对可分

对多类中的每两类构造一个分类器，所以每个模式类和其它模式类间可分别用判别平面分开，因此对于$c$类就有$\frac{c(c-1)}{2}$个决策面。

相较于“一对多”，决策歧义区域相对较小。

判别函数：$g_{ij}(x)=W_{ij}^{T}x$

判别边界：$g_{ij}(x)=0$

判别条件：$g_{ij}(x)\{\begin{array}{l}>0,当x\in w_1\\ <0,当x\in w_2\end{array}i\ne j$

判别函数性质：$g_{ij}(x)=g_{ji}(x)$

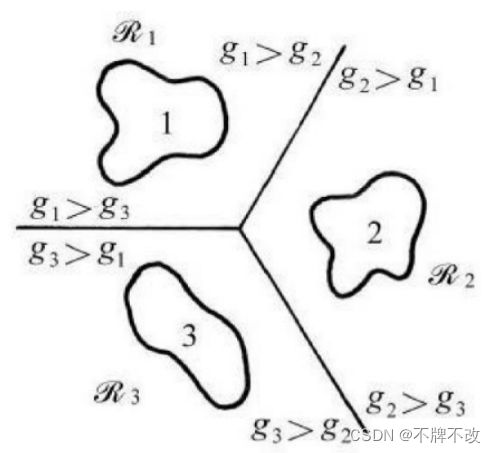
第三种情况：最大值判决

每类都有一个判别函数。

判别函数：$g_k(x)=W_{k}Xk=1,2,...,M$

判别规则：
$$g_i(x)=W_K^{T}X\{\begin{array}{l}最大,当x\in w_i\\ 小,其他\end{array}$$

判别边界：$g_i (x) =g_j (x) $或$g_i (x) -g_j (x) =0$

就是说，要判别模式$X$属于哪一类，先把$X$代入$M$个判别函数中，判别函数最大的那个类别就是$X$所属类别。

此分类实现方式也称作多类线性机器

多类线性机器不会出现有决策歧义的区域。下图显示三类的情况：

第一步：数据处理

对输入数据要进行主成分分析之前需要先对数据进行标准化处理，后续操作均是对标准化的数据集进行的。

第二步：PCA降维

观察前50个主成分，拐点出现在主成分3处且主成分3处相对效果较佳，所以将10304维降至3维收益较高。我选取降维至二维和三维进行模型效果对比。

第三步：维度-得分曲线

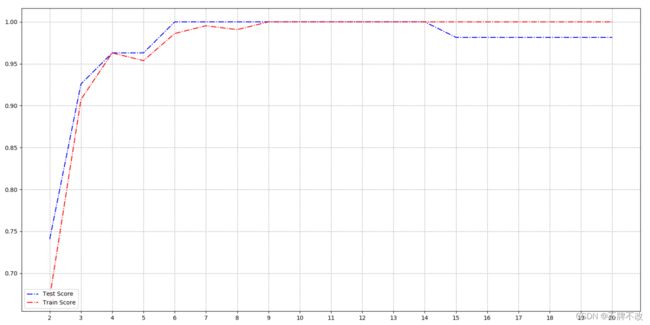
按20%划分测试集，用训练集训练PCA降维模型，对于不同维度分别得到训练集和测试集得分，绘制维度-得分曲线。

观察曲线可知，当降维至9及以上得分波动较小，且得分较高。为了可视化的方便，我依然采取了降维至二维和三维，但其实9维、10维等效果会更佳。

第四步：多分类模型

使用sklearn中自带的LinearDiscriminantAnalysis函数进行多分类，因为LDA本质上进行的是二分类，所以该函数默认使用OvR的方式进行多分类。

第五步：评价模型效果

降维至三维：

训练集与测试集的得分

test - Score: 0.93
train - Score: 0.91

交叉报告

              precision    recall  f1-score   support

          p1       0.89      0.89      0.89        18
          p2       0.89      0.89      0.89        18
          p3       1.00      1.00      1.00        18

    accuracy                           0.93        54
   macro avg       0.93      0.93      0.93        54
weighted avg       0.93      0.93      0.93        54

混淆矩阵

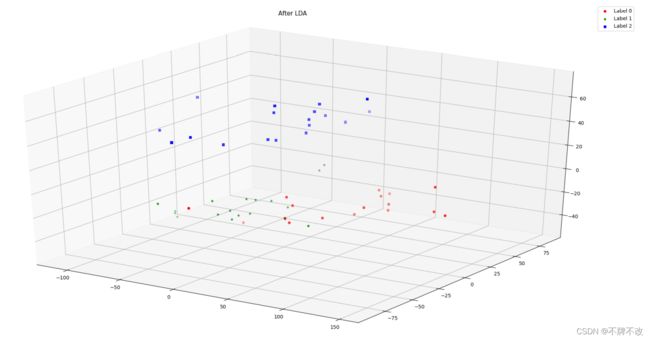
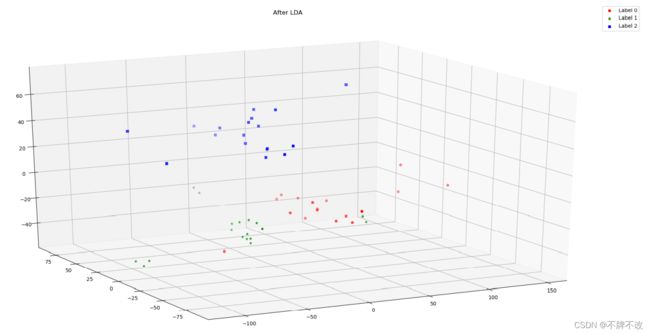
空间直角坐标系中显示测试集分类情况（多角度）

观察上述信息可以发现，三维分类效果比较理想，仅存在少数分错类的情况，对第三个人的区分正确率比较高。

降维至二维：

训练集与测试集的得分

test - Score: 0.74
train - Score: 0.67

交叉报告

              precision    recall  f1-score   support

          p1       0.84      0.89      0.86        18
          p2       0.63      0.67      0.65        18
          p3       0.75      0.67      0.71        18

    accuracy                           0.74        54
   macro avg       0.74      0.74      0.74        54
weighted avg       0.74      0.74      0.74        54

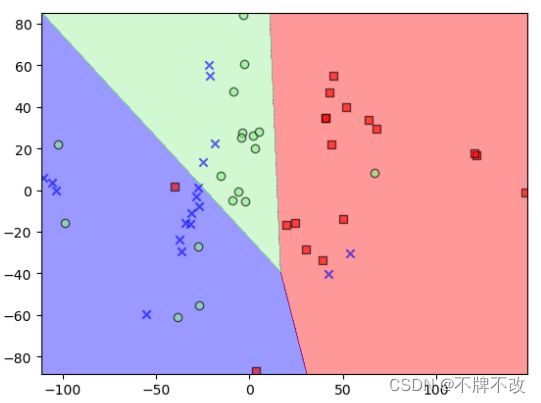
混淆矩阵

平面直角坐标系中显示测试集分类情况

观察上述信息可以发现，降维至2维对于分类存在较大误差，模型效果远不如降维至3维。

补充：与随机森林分类进行对比

随机森林的优点：

1. 可以处理高维度（特征很多）的数据，并且不用降维，无需做特征选择
2. 可以判断特征的重要程度
3. 可以判断出不同特征之间的相互影响
4. 不容易过拟合
5. 训练速度比较快，容易做成并行方法
6. 实现简单
7. 对于不平衡的数据集来说，可以平衡误
8. 如果有很大一部分的特征遗失，仍可以维持准确度

随机森林的缺点：

1. 随机森林已经被证明在某些噪音较大的分类或回归问题上会过拟合
2. 对于有不同取值的属性的数据，取值划分较多的属性会对随机森林产生更大的影响，所以随机森林在这种数据上产出的属性权值是不可信的

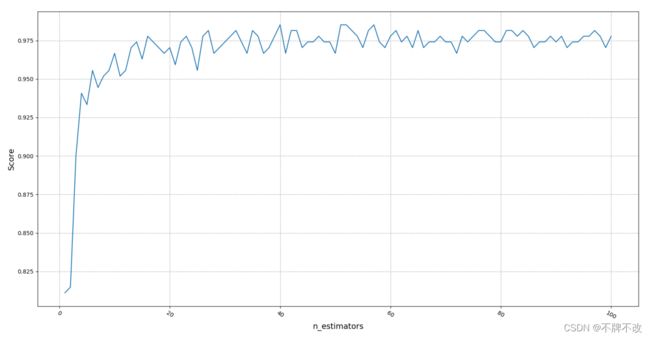
通过十折交叉验证进行随机森林分类，观察n_estimators（建树个数）的学习曲线。

观察发现当树的个数大于35左右时，分类准确率大概在0.975左右，后面即使增加树的个数，也没法再提高准确率了。

可见，随机森林的分类速度和分类效果都优于LDA。

附录1（实验一代码）

"""
该文件解决并可视化实验的第一问
"""

import numpy as np

dataSet = [[2.95, 6.63, 0],
           [2.53, 7.79, 0],
           [3.57, 5.65, 0],
           [3.16, 5.47, 0],
           [2.58, 4.46, 1],
           [2.16, 6.22, 1],
           [3.27, 3.52, 1]]

def split_feature_label(dataSet):
    x_0 = []
    x_1 = []

    for item in dataSet:
        if item[-1] == 0:
            x_0.append(item[:-1])
        else:
            x_1.append(item[:-1])

    x_0 = np.array(x_0)
    x_1 = np.array(x_1)

    return x_0, x_1

def LDA_2Classification(dataSet):
    x_0, x_1 = split_feature_label(dataSet)

    # 各类样本的均值向量
    mean_0 = np.mean(x_0, axis=0)  # 按列求均值，即每个特征的均值
    mean_1 = np.mean(x_1, axis=0)

    # 总样本类内散度矩阵
    # 其实就是协方差矩阵之和
    S_w = np.cov(x_0.T) + np.cov(x_1.T) # np.cov()求特征的协方差，默认一列表示一个样本，但我们传入的是一行表示一个样本，所以要先进行转置
    # 样本类间离散度矩阵
    S_b = np.matmul((mean_0 - mean_1).reshape(-1,1), (mean_0 - mean_1).reshape(1,-1))
    # reshape(-1,1)表示将ndarray变成一列，-1可以理解为通配，即必须保证列数为1，行数无所谓；
    # 如果ndaary总共12个元素，对其reshape(3,-1)表示变形成三行，自动得到列数为4；但是如果reshape(5,-1)则会报错，因为无法整除得到列数

    w = np.matmul(np.linalg.inv(S_w), (mean_0 - mean_1)) # 不理解矩阵和向量相乘？
    b = -1 * np.dot((mean_0 + mean_1) / 2, w) # 不理解，是经验吗？
    return w, b

def DisplayAllValue(dataSet, w, b):

    x_0, x_1 = split_feature_label(dataSet)

    value_0 = [(np.dot(w, item)+b) for item in x_0]
    value_1 = [(np.dot(w, item)+b) for item in x_1]

    print(value_0)
    print(value_1)

    return value_0, value_1

def Discriminant_function(sample, w, b): # 判别函数，返回判别函数值
    return np.dot(w, sample)+b

def Plot_LDA_2Classification(dataSet, w, b): # 仅能绘制两个特征的空间分布
    import numpy as np
    import matplotlib as mpl
    import matplotlib.pyplot as plt
    from mpl_toolkits.mplot3d import Axes3D
    from matplotlib import cm

    x = np.arange(0, 10, 0.25)
    y = np.arange(0, 10, 0.25)
    x, y = np.meshgrid(x,y) # 网格

    mpl.rcParams['legend.fontsize'] = 20  # mpl模块载入的时候加载配置信息存储在rcParams变量中，rc_params_from_file()函数从文件加载配置信息
    font = {
        'color': 'b',
        'style': 'oblique',
        'size': 30,
        'weight': 'bold'
    }
    fig = plt.figure(figsize=(16, 12))  #参数为图片大小
    ax = fig.gca(projection='3d')  # get current axes，且坐标轴是3d的
    ax.set_xlim(0, 10)
    ax.set_ylim(0, 10)
    ax.set_xlabel('参数A')
    ax.set_ylabel('参数B')
    ax.set_aspect('equal')  # 坐标轴间比例一致
    plt.rcParams['font.family'] = ['sans-serif']
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus']=False

    x_0, x_1 = split_feature_label(dataSet)

    ax.scatter(x_0[:,0], x_0[:,1], [Discriminant_function(i, w, b)*20 for i in x_0], marker='o', label='合格', s=70) # 对z坐标额外乘了20，方便观察
    ax.scatter(x_1[:,0], x_1[:,1], [Discriminant_function(i, w, b)*20 for i in x_1], marker='+', label='不合格', s=70)
    surf = ax.plot_surface(x, y, w[0]*x+w[1]*y+b, cmap='Greys')
    ax.legend(loc="upper left")

    plt.show()


if __name__=='__main__':
    w, b = LDA_2Classification(dataSet) # 得到w和b
    print(w, b)
    DisplayAllValue(dataSet, w, b) # 显示每个样本的判别函数值
    Plot_LDA_2Classification(dataSet, w, b) # 绘图

附录2（实验二代码）

Matlab代码：

%% 数据集扩充
nPerson=40;
nFacesPerPerson = 10;

% 只需运行一次即可
% 数据集扩充
display('数据集扩展...');
Path = 'E:/VirtualDesktop/faces/orl_faces';
saveTo = 'FaceMat_Ori.mat';
[imgRow,imgCol,FaceContainer,faceLabel]=ReadFaces(nFacesPerPerson,nPerson, Path, saveTo);
load(saveTo); % 导入FaceContainer变量
DealOriginalDataSet(FaceContainer, 40, 10); % 需要先通过ReadFaces函数得到FaceMat_Ori.m
display('..............................');

%% 获取前两个人的数据
nPerson = 2;
nFacesPerPerson = 90;
display('读入人脸数据...');
Path = 'E:/VirtualDesktop/faces/ORL_extend';
saveTo = 'FaceMat_Extend.mat';
[imgRow,imgCol,FaceContainer,faceLabel]=ReadFaces(nFacesPerPerson, nPerson, Path, saveTo);
display('..............................');
xlswrite('C:/Users/23343/Desktop/dataset2.xlsx', FaceContainer)

%% 可视化降维后的特征
w = xlsread('C:\Users\23343\Desktop\w.xlsx');
% 特征显示
row = 112;
col = 92;
img = zeros(row, col); 
figure
for i = 1:3
    img(:) = w(:, i);
    subplot(1, 3, i);
    imshow(img, []); 
end

function [imgRow,imgCol,FaceContainer,faceLabel]=ReadFaces(nFacesPerPerson, nPerson, Path, saveTo)
% 读入ORL人脸库的指定数目的人脸
%
% 输入：nFacesPerPerson --- 每个人需要读入的样本数
%       nPerson --- 需要读入的人数
%       Path --- 照片所在路径
%       saveTo --- 变量保存路径
%
% 输出：FaceContainer --- 向量化人脸容器，nPerson * 10304 的 2 维矩阵，每行对应一个人脸向量

% Path = 'E:/VirtualDesktop/faces/ORL_extend';
% Path = 'E:/VirtualDesktop/faces/orl_faces';
% saveTo = 'FaceMat_Extend.mat';
% saveTo = 'FaceMat_Ori.mat';

img=imread(strcat(Path, '/s1/1.pgm'));%为计算尺寸先读入一张
[imgRow,imgCol]=size(img);


FaceContainer = zeros(nFacesPerPerson*nPerson, imgRow*imgCol);
faceLabel = zeros(nFacesPerPerson*nPerson, 1);

% 读入训练数据
for i=1:nPerson  
    i1=mod(i,10); % 个位
    i0=char(i/10); % 十位
    
    strPath=strcat(Path,'/s');
    if( i0~=0 )
        strPath=strcat(strPath,'0'+i0);
    end
    strPath=strcat(strPath,'0'+i1);
    strPath=strcat(strPath,'/');
    tempStrPath=strPath;
    for j=1:nFacesPerPerson
        ge = mod(j, 10); % 个位
        sh = floor(j/10); % 十位
        strPath=tempStrPath;

        if sh ~= 0
            strPath = strcat(strPath, '0'+sh); % +'0'的意思是将数字j转换为对应的字符，因为只有字符可以做拼接
        end
        strPath = strcat(strPath, '0'+ge);
        
        strPath=strcat(strPath,'.pgm');
        img=imread(strPath);

        %把读入的图像按列存储为行向量放入向量化人脸容器faceContainer的对应行中
        FaceContainer((i-1)*nFacesPerPerson+j, :) = img(:)'; %FaceContainer一行是一张照片
        faceLabel((i-1)*nFacesPerPerson+j) = i;
    end % j
end % i

% 保存人脸样本矩阵
save(saveTo, 'FaceContainer') % 将变量FaceContainer保存在FaceMat.mat中

function DealOriginalDataSet(dataset, nPerson, nFacesPerPerson) % dataset为ReadFaces函数得到的矩阵，
    
    row = 112;
    col = 92;
    rootPath = 'E:/VirtualDesktop/faces/ORL_extend';

    for i = 1:nPerson
        ge = mod(i, 10); % 个位
        sh = floor(i/10); % 十位
        filePath = strcat(rootPath, '/s');
        if sh ~= 0
            filePath = strcat(filePath,'0'+ sh);
        end
        filePath = strcat(filePath,'0'+ ge);
        mkdir(filePath);
        
        for j = 1:nFacesPerPerson
            sample = dataset((i-1)*nFacesPerPerson+j,:);
            I = uint8(reshape(sample, row, col));
            [I_ori, I_mirror, I_dark, I_bright, I_leftmove, I_rightmove, I_shun10, I_ni10] = ExtendDataSet(I);
            Is = [I, I_ori, I_mirror, I_dark, I_bright, I_leftmove, I_rightmove, I_shun10, I_ni10];
            
            for k = 1:9 % 一张图经过变形得到9张图，其中两张是原图
                gege = mod((j-1)*9+k, 10); % 个位
                shsh = floor(((j-1)*9+k) / 10); % 十位
                
                picPath = strcat(filePath,  '/');
                if shsh ~= 0
                    picPath = strcat(picPath, '0' + shsh);
                end
                picPath = strcat(picPath, '0' + gege, '.pgm');
                
                imwrite(Is(:,col*(k-1)+1:col*k), picPath);
            end
            
%             imwrite(I, picPath);
%             imwrite(I, picPath);
%             imwrite(I_mirror, picPath);
%             imwrite(I_dark, picPath);
%             imwrite(I_bright, picPath);
%             imwrite(I_leftmove, picPath);
%             imwrite(I_rightmove, picPath);
%             imwrite(I_shun10, picPath);
%             imwrite(I_ni10, picPath);
            
%             figure;
%             subplot(241), imshow(I), title('原图');
%             subplot(242), imshow(I_mirror), title('左右镜像');
%             subplot(243), imshow(I_dark), title('变暗');
%             subplot(244), imshow(I_bright), title('变亮');
%             subplot(245), imshow(I_leftmove), title('左移10像素');
%             subplot(246), imshow(I_rightmove), title('右移10像素');
%             subplot(247), imshow(I_shun10), title('顺时针旋转10°');
%             subplot(248), imshow(I_ni10), title('逆时针旋转10°');
        end
    end
end

function [I, I_mirror, I_dark, I_bright, I_leftmove, I_rightmove, I_shun10, I_ni10] = ExtendDataSet(I)

    background = double(42);                                    % 背景色

    I_dark = I-30;                                              % 图像变暗
    I_bright = I+30;                                            % 图像变亮
    I_mirror = I(:,end:-1:1);                                   % 图像左右镜像
    I_leftmove = I;
    row = size(I, 1); 
    col = size(I, 2);
    tmp = uint8(background * ones(row, 10));                    % 相等于要移动十个像素
    I_leftmove(:,1:end-10) = I_leftmove(:,11:end);               % 左移10个像素
    I_leftmove(:,end-9:end) = tmp;

    I_rightmove = I;
    I_rightmove(:,11:end) = I_rightmove(:,1:end-10);
    I_rightmove(:,1:10) = tmp;

    a = 12;
    b = 50;
    threshold = 40;                                             % 阈值，用于对旋转后的图像周围进行填充

    I_shun10 = imrotate(I, 10, 'bicubic', 'crop');              % 逆时针10°旋转                                   
    for i = 1:row
        for j = 1:col
            if I_shun10(i,j) >= threshold                       % 灰度值超过阈值则无需改变，说明是原图内容
                continue
            end
            if (icol-a) || (i>row-b && jrow-a && j>col-b)     % 当未超过阈值灰度值且位于四个角时，填充为背景色
                I_shun10(i,j) = background;
            end
        end
    end

    I_ni10 = imrotate(I, -10, 'bicubic', 'crop');               % 顺时针10°旋转
    for i = 1:row
        for j = 1:col
            if I_ni10(i,j) >= threshold
                continue
            end
            if (icol-b) || (i>row-a && jrow-b && j>col-a)
                I_ni10(i,j) = background;
            end
        end
    end
end

Python代码：

"""
该文件可以显示主成分分析效果
"""
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

row = 112
col = 92

x = pd.read_excel(r'C:\Users\23343\Desktop\dataset2.xlsx', header=None) # 默认读取到这个Excel的第一个表单，且不让第一行数据作为列索引
# data=df.head() # 默认读取前5行的数据
# print("获取到所有的值:\n{0}".format(data)) # 格式化输出
y = np.append(np.zeros((90, 1)), np.ones((90, 1)), axis=0) # label

from sklearn.preprocessing import StandardScaler
# Normalize the  data (center around 0 and scale to remove the variance).
xs =StandardScaler().fit_transform(x)

from sklearn.decomposition import PCA
# 从 row*col维 降到 50 维
pca = PCA(n_components=50)
pca.fit(xs)

#The amount of variance that each PC explains
var = pca.explained_variance_ratio_
### 通过拐点确定选择前几个PC
plt.plot(var)
plt.title('Scree Plot')
plt.xlabel('Principal Component')
plt.ylabel('Eigenvalue')
plt.xticks(np.arange(0, 50, 1), rotation=-30)
leg = plt.legend(['Eigenvalues from PCA'],
                 loc='best',
                 borderpad=0.3,
                 shadow=False,
                 markerscale=0.4)

leg.get_frame().set_alpha(0.4)
leg.draggable(state=True)

plt.grid()
# plt.show()

# 通过上面显示50个主成分我们发现只有前3个主成分的无关性较好，所以选择前3个主成分
pca = PCA(n_components=3)
fit = pca.fit(xs)
x_pca = pca.transform(xs) # 将标准化的原始数据集降维成3维
# print(pca.components_.shape) # 3*10304
new_x = x.dot(pca.components_.T) # 对原始的数据集进行转换
w = pd.DataFrame(pca.components_.T)
w.to_excel(r'C:\Users\23343\Desktop\w.xlsx', index=False, header=None) # 不写入行列索引

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split

"""
该函数实现训练和预测
"""

def Discriminant_function(sample, w, b): # 判别函数，返回判别函数值
    return np.dot(w, sample)+b

def split_feature_label(dataSet, label):
    x_0 = []
    x_1 = []

    for i in range(0, dataSet.shape[0]):
        if label[i] == 0:
            x_0.append(dataSet[i,:])
        else:
            x_1.append(dataSet[i,:])

    x_0 = np.array(x_0)
    x_1 = np.array(x_1)

    return x_0, x_1

def LDA_2Classification(dataSet, label):
    x_0, x_1 = split_feature_label(dataSet, label)

    # 各类样本的均值向量
    mean_0 = np.mean(x_0, axis=0)  # 按列求均值，即每个特征的均值
    mean_1 = np.mean(x_1, axis=0)

    # 总样本类内散度矩阵
    # 其实就是协方差矩阵之和
    S_w = np.cov(x_0.T) + np.cov(x_1.T) # np.cov()求特征的协方差，默认一列表示一个样本，但我们传入的是一行表示一个样本，所以要先进行转置
    # 样本类间离散度矩阵
    S_b = np.matmul((mean_0 - mean_1).reshape(-1,1), (mean_0 - mean_1).reshape(1,-1))
    # reshape(-1,1)表示将ndarray变成一列，-1可以理解为通配，即必须保证列数为1，行数无所谓；
    # 如果ndaary总共12个元素，对其reshape(3,-1)表示变形成三行，自动得到列数为4；但是如果reshape(5,-1)则会报错，因为无法整除得到列数

    w = np.matmul(np.linalg.inv(S_w), (mean_0 - mean_1)) # 不理解矩阵和向量相乘？
    b = -1 * np.dot((mean_0 + mean_1) / 2, w) # 不理解，是经验吗？
    return w, b

def predict(test, w, b):
    test_label = []
    for item in test:
        value = Discriminant_function(item, w, b)
        test_label.append(0 if (value > 0) else 1)
    return test_label

def Fisher(dataSet, label): # 传入降维后的矩阵且带标签 (ndarray)
    X_train, X_test, Y_train, Y_test = train_test_split(dataSet, label, test_size=0.1)

    w, b = LDA_2Classification(X_train, Y_train)

    print(w, b)
    print('------- 得到w和b -------')

    # ----- 输出观察 -----
    # for i in range(0, X_test.shape[0]) :
    #     value = Discriminant_function(X_test[i,:], w, b)
    #     print(Y_test[i, 0], value, end=' ')
    #     if (((value > 0) & (Y_test[i, 0] == 0)) | ((value < 0) & (Y_test[i, 0] == 1))):
    #         print('True')
    #     else:
    #         print('False')
    # ------------------

    test_label_predict = predict(X_test, w, b)
    print('----- 得到预测集对应的标签 -----')
    test_label_original = [item[0] for item in Y_test]
    print(test_label_original)
    print(test_label_predict)
    # 交叉报告(classfication_report)是几个指标（精确率、召回率、f1-score）的一个汇总情况。
    from sklearn.metrics import classification_report
    target_names = ['p1', 'p2']
    print(classification_report(test_label_original, test_label_predict, target_names=target_names))
    plotConfusionMatrix(test_label_original, test_label_predict)
    # plotROC(test_label_original, test_label_predict)

def plotConfusionMatrix(test_label_original, test_label_predict): # 混淆矩阵
    from sklearn.metrics import confusion_matrix
    cm = confusion_matrix(test_label_original, test_label_predict)
    fig, ax = plt.subplots(figsize=(5, 5))
    ax.matshow(cm, cmap=plt.cm.Greens, alpha=0.3)
    for i in range(cm.shape[0]):
        for j in range(cm.shape[1]):
            ax.text(x=j, y=i,
                    s=cm[i, j],
                    va='center', ha='center')
    plt.xlabel('Predicted Values')
    plt.ylabel('Actual Values')
    plt.show()

def plotROC(test_label_original, test_label_predict):
    """
    使用ROC曲线描述Fisher二分类的模型优劣还有待商榷，因为roc_curve的第二个参数为得到正确标签的概率（或得分），而Fisher会直接得到结果，不存在概率
    或许通过一个激活函数，类似于sigmoid函数，可以将Fisher得到的估值概率化，从而调用roc_curve
    :param test_label_original:
    :param test_label_predict:
    :return:
    """
    # 导入库
    from sklearn.metrics import roc_curve, auc
    # 计算tpr,fpr,auc
    print(test_label_original)
    print(test_label_predict)
    fpr, tpr, threshold = roc_curve(test_label_original, test_label_predict)
    roc_auc = auc(fpr, tpr)
    print('area = ', roc_auc)
    print(fpr)
    print(tpr)
    print(threshold)
    # plot roc_curve
    plt.figure(figsize=(10,10))
    lw = 2
    plt.plot(fpr, tpr, color='darkorange', lw=lw, label='ROC curve')
    plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
    plt.xlim([0.0, 1.0])
    plt.ylim([0.0, 1.05])
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
    plt.title('Receiver operating characteristic example')
    plt.legend(loc="lower right")
    plt.show()

if __name__=='__main__':
    w = pd.read_excel(r'C:\Users\23343\Desktop\w.xlsx', header=None)
    dataSet = pd.read_excel(r'C:\Users\23343\Desktop\dataset2.xlsx', header=None)
    w = np.array(w)
    label = np.append(np.zeros((90, 1), dtype=int), np.ones((90, 1), dtype=int), axis=0)
    dataSet = np.matmul(np.array(dataSet), w)
    print("-------数据导入完成--------")

    Fisher(dataSet, label)

附录3（实验三代码）

"""

实现三分类:
1. PCA降维到2维（等高线分割）
2. PCA降维到3维（空间显示）

"""

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

def load_data():
    X = pd.read_excel(r'C:\Users\23343\Desktop\dataset3.xlsx', header=None)
    Y = np.zeros((90, 1)) # 根据X的行数自动生成标签
    for i in range(1, int(X.shape[0]/90)):
        Y = np.append(Y, i*np.ones((90, 1)), axis=0)
    Y = Y.astype(int)
    return X, Y

def analyse_data(X):
    from sklearn.decomposition import PCA
    from sklearn.preprocessing import StandardScaler

    X_std = StandardScaler().fit_transform(X)
    pca = PCA(n_components=50)
    pca.fit(X_std)
    plt.plot(pca.explained_variance_ratio_)
    plt.title('Scree Plot')
    plt.xlabel('Principal Component')
    plt.ylabel('Eigenvalue')
    plt.xticks(np.arange(0, 50, 1), rotation=-30)
    plt.grid(ls='--')
    leg = plt.legend(['Eigenvalues from PCA'],
                     loc='best',
                     borderpad=0.3,
                     shadow=False,
                     markerscale=0.4)
    leg.get_frame().set_alpha(0.4)
    leg.draggable(state=True)
    plt.show()

    return X_std

def split_dataset(X, Y, seed = 30):
    from sklearn.model_selection import train_test_split

    X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=seed)
    return X_train, X_test, Y_train, Y_test

def dimension_reduction(X, downto):
    """
    PCA降维
    :param X: 标准化后的特征，三分类中270*10304
    :param downto: 降到dowto维度，一般选2或3
    :return: X_pca为降维后的特征，270*3；w为降维矩阵
    """
    from sklearn.decomposition import PCA

    pca = PCA(n_components=downto)
    X_pca = pca.fit_transform(X) # 将标准化后的数据集降维成downto维  # 270*3 # 等价于X.dot(pca.components_.T)
    w = pca.components_.T # 10304*3，用于降维的矩阵
    return X_pca, w

def train_model(X, Y, OvR = True): # 这里传入X和Y都是训练集的特征和标签
    from sklearn import discriminant_analysis

    # LinearDiscriminantAnalysis实现多分类默认OvR
    lda = discriminant_analysis.LinearDiscriminantAnalysis().fit(X, Y.ravel()) # 默认使用OvR方式

    return lda

def plot_dimension_reduction_curve(X, n):
    test_score = []
    train_score = []

    for downto in range(2, n+1):
        X_tmp, w = dimension_reduction(X, downto)  # 返回值X为降维后的特征，w为降维矩阵
        X_train, X_test, Y_train, Y_test = split_dataset(X_tmp, Y)  # 划分训练集和测试集
        model = train_model(X_train, Y_train)
        test_score.extend([model.score(X_test, Y_test)])
        train_score.extend([model.score(X_train, Y_train)])

    plt.plot(np.arange(2, n+1).astype(np.str), test_score, '-.b')
    plt.plot(np.arange(2, n+1).astype(np.str), train_score, '-.r',)
    plt.legend(['Test Score', 'Train Score'], loc='lower left')
    plt.grid(ls='--')
    plt.show()

def plot_confusion_matrix(test_label_original, test_label_predict): # 混淆矩阵
    from sklearn.metrics import confusion_matrix
    cm = confusion_matrix(test_label_original, test_label_predict)
    fig, ax = plt.subplots(figsize=(5, 5))
    ax.matshow(cm, cmap=plt.cm.Greens, alpha=0.3)
    for i in range(cm.shape[0]):
        for j in range(cm.shape[1]):
            ax.text(x=j, y=i,
                    s=cm[i, j],
                    va='center', ha='center')
    plt.xlabel('Predicted Values')
    plt.ylabel('Actual Values')
    plt.show()

def plot_random_forest_precision_curve(X, Y, n=100):
    from sklearn.model_selection import train_test_split
    from sklearn.model_selection import cross_val_score
    from sklearn.ensemble import RandomForestClassifier

    X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.3)
    superpa = []
    for i in range(n):
        print(i)
        rfc = RandomForestClassifier(n_estimators=i+1, n_jobs=-1, max_features=0.001, max_depth=10)
        rfc_s = cross_val_score(rfc, X, Y.ravel(), cv=10).mean()
        superpa.append(rfc_s)
    # print(max(superpa),superpa.index(max(superpa)))
    plt.figure(figsize=[20,5])
    plt.plot(np.arange(1,n+1),superpa)
    plt.xticks(rotation=-30)
    plt.ylabel('Score', fontsize=14)
    plt.xlabel('n_estimators', fontsize=14)
    plt.grid(ls='--')
    plt.show()

def plt_in_2D_rectangular_coordinate_system(X, Y, classifier):
    from matplotlib.colors import ListedColormap
    # setup marker generator and color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(Y))])

    # plot the decision surface
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, 0.02),
                           np.arange(x2_min, x2_max, 0.02))
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)  # 转置后每行两个特征，行数为样本数
    Z = Z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)  # 绘制等高线，其实就是实现了区域的划分，同一类的Z值相等，即高度相等，颜色一样。
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())

    # plot class samples
    for idx, cl in enumerate(np.unique(Y)):
        Y_tmp = Y.ravel()
        plt.scatter(x=X[Y_tmp == cl, 0],
                    y=X[Y_tmp == cl, 1],
                    alpha=0.6,  # 透明度
                    c=cmap(idx),
                    edgecolor='black',
                    marker=markers[idx],
                    label=cl)
    plt.show()

def plt_in_3D_rectangular_coordinate_system(X, Y): # 一般传入测试集
    from mpl_toolkits.mplot3d import Axes3D
    fig = plt.figure()
    ax = Axes3D(fig)
    colors = 'rgb'
    markers = 'o*s'
    for target, color, marker in zip([0, 1, 2], colors, markers):
        pos = (Y == target).ravel() # 所有标签为target的赋值为true，否则为false
        X_tmp = X[pos, :]
        ax.scatter(X_tmp[:, 0], X_tmp[:, 1], X_tmp[:, 2], color=color, marker=marker,
                   label="Label %d" % target)
    ax.legend(loc="best")
    fig.suptitle("After LDA")
    plt.show()

def evluate_model(model, X_train, Y_train, X_test, Y_test, downto):
    """
    用于模型评估，包括训练集和测试集的得分、测试集混淆矩阵、测试集交叉报告、在空间直角坐标系中展示测试集的分类情况
    :param model: 模型
    :param X_train: 训练集特征
    :param Y_train: 训练集标签
    :param X_test:  测试集特征
    :param Y_test:  测试集标签
    :param downto:  模型降维至多少
    :return: None
    """
    print('test - Score: %.2f' % model.score(X_test, Y_test))  # 测试集
    print('train - Score: %.2f' % model.score(X_train, Y_train))  # 训练集

    plot_confusion_matrix(Y_test, model.predict(X_test))  # 绘制测试集的混淆矩阵

    from sklearn.metrics import classification_report
    print(classification_report(Y_test, model.predict(X_test), target_names=['p1', 'p2', 'p3'])) # 交叉报告

    if downto == 3:
        plt_in_3D_rectangular_coordinate_system(X_test, Y_test) # 绘制空间直角坐标系中的分类情况
    else:
        plt_in_2D_rectangular_coordinate_system(X_test, Y_test, model) # 绘制平面直角坐标系中的分类情况

if __name__=='__main__':
    X, Y = load_data() # 导入数据并生成标签
    print("--------------- 数据导入完毕 ------------------")
    plot_random_forest_precision_curve(X, Y) # 绘制随机森林的效果与决策树数量的变化曲线 # 比较慢

    X = analyse_data(X) # 绘图显示50个主成分，返回值为标准化后的特征

    plot_dimension_reduction_curve(X, 20) # 绘制降维到2~20个特征时训练集和测试集的得分曲线

    # -------------- 降至3维 -------------- #
    X, w = dimension_reduction(X, 3)  # 返回值X为降维后的特征，w为降维矩阵
    X_train, X_test, Y_train, Y_test = split_dataset(X, Y)  # 划分训练集和测试集
    model = train_model(X_train, Y_train)
    evluate_model(model, X_train, Y_train, X_test, Y_test, 3) # 模型评估函数

    # -------------- 降至2维 -------------- #
    X, w = dimension_reduction(X, 2)  # 返回值X为降维后的特征，w为降维矩阵
    X_train, X_test, Y_train, Y_test = split_dataset(X, Y)  # 划分训练集和测试集
    model = train_model(X_train, Y_train)
    print(X_test.shape, Y_test.shape)
    evluate_model(model, X_train, Y_train, X_test, Y_test, 2) # 模型评估函数