m05_Extract Feature_Transformers(慎variances_)_download Adult互联网ads数据集_null value(?_csv_SVD_PCA_eigen

     The datasets we have used so far have been described in terms of features. In the m04_Recommending Movies w Affinity Analysis_Apriori_sys.stdout.flush_df.iterrows_Sort nested dict嵌套_Linli522362242的专栏-CSDN博客, we used a transaction-centric dataset. However, ultimately this was just a different format for representing feature-based data.

     There are many other types of datasets, including text, images, sounds, movies, or even real objects. Most data mining algorithms, however, rely on having numerical or categorical features. This means we need a way to represent these types before we input them into the data mining algorithm.

     In this chapter, we will discuss how to extract numerical and categorical features, and choose the best features when we do have them. We will discuss some common patterns and techniques for extracting features.

The key concepts introduced in this chapter include:

• • Extracting features from datasets
• • Creating new features
• • Selecting good features
• • Creating your own transformer for custom datasets

Feature extraction

     Extracting features is one of the most critical tasks in data mining, and it generally affects your end result more than the choice of data mining algorithm. Unfortunately, there are no hard and fast rules for choosing features that will result in high performance data mining. In many ways, this is where the science of data mining becomes more of an art. Creating good features relies on intuition, domain expertise, data mining experience, trial and error, and sometimes a little luck.

     The difference between feature selection and feature extraction提取 is that while we maintain the original features when we used feature selection algorithms, such as sequential backward selection, we use feature extraction to transform or project the data onto a new feature space. In the context of dimensionality reduction, feature extraction can be understood as an approach to data compression with the goal of maintaining most of the relevant information. In practice, feature extraction is not only used to improve storage space or the computational efficiency of the learning algorithm, but can also improve the predictive performance by reducing the curse of dimensionality—especially if we are working with non-regularized models.

Representing reality in models

     Not all datasets are presented in terms of features. Sometimes, a dataset consists of nothing more than all of the books that have been written by a given author. Sometimes, it is the film of each of the movies released in 1979. At other times, it is a library collection of interesting historical artifacts.

     From these datasets, we may want to perform a data mining task. For the books, we may want to know the different categories that the author writes. In the films, we may wish to see how women are portrayed[pɔːrˈtreɪ]描绘. In the historical artifacts, we may want to know whether they are from one country or another. It isn't possible to just pass these raw datasets into a decision tree and see what the result is.

     For a data mining algorithm to assist us here, we need to represent these as features. Features are a way to create a model and the model provides an approximation of reality in a way that data mining algorithms can understand. Therefore, a model is just a simplified version of some aspect of the real world. As an example, the game of chess is a simplified model for historical warfare[ˈwɔːfeə(r)] 战争.

     Selecting features has another advantage: they reduce the complexity of the real world into a more manageable model. Imagine how much information it would take to properly[ˈprɑːpərli] 恰当地, accurately, and fully describe a real-world object to someone that has no background knowledge of the item. You would need to describe the size, weight, texture[ˈtekstʃər]质地, composition, age, flaws瑕疵, purpose, origin产地, and so on.

     The complexity of real objects is too much for current algorithms, so we use these simpler models instead.

     This simplification also focuses our intent[ɪnˈtent]目的，意图 in the data mining application. In later chapters, we will look at clustering and where it is critically important至关重要. If you put random features in, you will get random results out.

     However, there is a downside as this simplification reduces the detail, or may remove good indicators of the things we wish to perform data mining on.

     Thought should always be given to how to represent reality in the form of a model. Rather than just using what has been used in the past, you need to consider the goal of the data mining exercise. What are you trying to achieve? In m03 Predicting Sports Winners with Decision Trees_NBA_TP_metric_OneHotEncoder_bias_colab_Linli522362242的专栏-CSDN博客, Predicting Sports Winners with Decision Trees, we created features by thinking about the goal (predicting winners) and used a little domain knowledge to come up with ideas for new features.

     Not all features need to be numeric or categorical. Algorithms have been developed that work directly on text, graphs, and other data structures. In this book, we mainly use numeric or categorical features.

     The Adult dataset is a great example of taking a complex reality and attempting to model it using features. In this dataset, the aim is to estimate if someone earns more than $50,000 per year. To download the dataset, navigate to Index of /ml/machine-learning-databases/adult and click on the Data link. Download the adult.data and adult.names into a directory named Adult in your data folder.

###############################

download file:

cp8_Sentiment_urlretrieve_pyprind_tarfile_bag词袋_walk目录_regex_verbose_N-gram_Hash_colab_verbose_文本向量化_Linli522362242的专栏-CSDN博客

import urllib.request
import time
import sys
import os

dataset_filename = 'adult.data'
dataset_URL = 'http://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.data'
 
def reporthook(count, block_size, total_size):
    global start_time
    if count==0:
        start_time = time.time()
        return
    time.sleep(1) # 1 second
    duration = time.time() - start_time
    progress_size = int(count*block_size)
    currentLoad = progress_size/(1024.**2)
    speed = currentLoad / duration # 1024.**2 <== 1MB=1024KB, 1KB=1024Btyes
    percent = count * block_size * 100./total_size
    sys.stdout.write("\r%d%% | %d MB | speed=%.2f MB/s | %d sec elapsed" %
                     (percent, currentLoad, speed, duration)
                    )
    sys.stdout.flush()
 
# if not exists file ('adult.data') then download...
if not os.path.isfile( dataset_filename ):
    # urllib.request.urlretrieve(url, filename=None, reporthook=None, data=None)
    # The third argument, if present, is a callable that will be called once on establishment of 
    # the network connection and once after each block read thereafter. 
    # The callable will be passed three arguments; a count of blocks transferred so far, 
    #                                              a block size in bytes, 
    #                                              and the total size of the file. (bytes)
    urllib.request.urlretrieve(dataset_URL, dataset_filename, reporthook)

OR

import requests

dataset_filename = 'adult.data'
dataset_URL = 'http://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.data'
 
r = requests.get(dataset_URL )
 
with open(dataset_filename, 'wb') as f:
    f.write( r.content )

Read online data:

     This dataset takes a complex task and describes it in features. These features describe the person, their environment, their background, and their life status.

import pandas as pd

url_adult = 'http://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.data'

adult = pd.read_csv( url_adult, header=None,
                     names=["Age", "Work-Class", "fnlwgt", "Education",
                            "Education-Num", "Marital-Status", "Occupation",
                            "Relationship", "Race", "Sex", "Capital-gain",
                            "Capital-loss", "Hours-per-week", "Native-Country",
                            "Earnings-Raw"
                           ]
                   )
adult.iloc[10:20]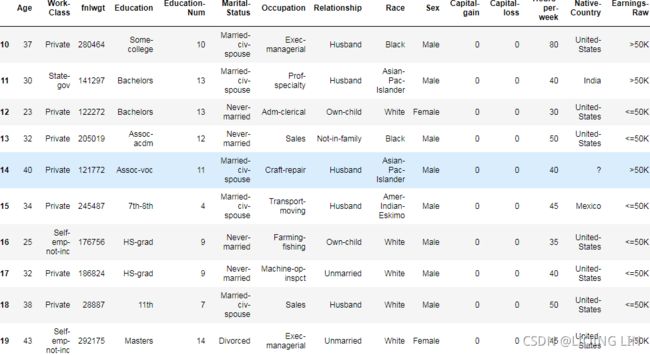

Dealing with missing data

cp4 Training Sets Preprocessing_StringIO_dropna_categorical_feature_Encode_Scale_L1_L2_bbox_to_ancho_Linli522362242的专栏-CSDN博客

adult.dtypes

There is a situation here, the null value in the data set is the'?' character, sometimes it can be detected to use df.isin(['?']).any(),
#########################
for example,n3_knn breastCancer NaiveBayesLikelihood_voter_manhat_Euclid_Minkow_空值?_SBS特征选取_Laplace_zip_NLP_spam_Linli522362242的专栏-CSDN博客

breast_cancer.isin(['?']).any()

#########################
sometimes it cannot be like the following situation

adult.isin(['?']).any()

 

adult.isnull().any() # isnull : Alias of isna.

 
solutions:

import numpy as np
adult = adult.replace( to_replace=r'\?', value=np.nan, regex=True)
adult.iloc[10:16]

adult.isna().any()

 

adult.shape

 

adult.isnull().sum(axis=0)

 

adult.dropna(inplace=True)
# OR adult = adult.dropna(inplace=False) # inplace = False will return a modified object, so we need to save it

adult.isnull().any()

adult[10:16]

 Note: Because the original 14th row existed a null value (NAN), it was deleted.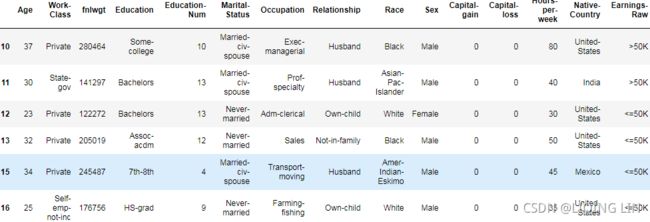

 ###############################

import pandas as pd

url_adult = 'http://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.data'

adult = pd.read_csv( url_adult, # or 'adult.data',
                     sep=',',
                     keep_default_na=False,
                     header=None,
                     names=["Age", "Work-Class", "fnlwgt", "Education",
                            "Education-Num", "Marital-Status", "Occupation",
                            "Relationship", "Race", "Sex", "Capital-gain",
                            "Capital-loss", "Hours-per-week", "Native-Country",
                            "Earnings-Raw"
                           ]
                   )

     The adult file itself contains two blank lines at the end of the file. By default, pandas will interpret the penultimate new line to be an empty (but valid) row. To remove this, we remove any line with invalid numbers (the use of inplace just makes sure the same Dataframe is affected, rather than creating a new one):

adult[-5:]

     We do not have this situation here, because pandas is a new version, which solves this problem.

    If it is a low version of pandas, add the following code

adult.dropna( how='all', inplace=True )

Having a look at the dataset, we can see a variety of features from adult.columns:

adult.columns

     The results show each of the feature names that are stored inside an Index object from pandas:

Common feature patterns

     While there are millions of ways to create features, there are some common patterns that are employed across different disciplines[ˈdɪsəplɪnz]学科,科目. However, choosing appropriate features is tricky and it is worth considering how a feature might correlate to the end result. As the adage[ˈædɪdʒ]谚语 says, don't judge a book by its cover—it is probably not worth considering the size of a book if you are interested in the message contained within.

     Some commonly used features focus on the physical properties of the real world objects being studied, for example:

• • Spatial properties such as the length, width, and height of an object
• • Weight and/or density of the object
• • Age of an object or its components
• • The type of the object
• • The quality of the object

Other features might rely on the usage or history of the object:

• • The producer, publisher, or creator of the object
• • The year of manufacturing
• • The use of the object使用方法

Other features describe a dataset in terms of its components根据其组件/组成成分角度描述数据集:

• • Frequency of a given subcomponent, such as a word in a book
• • Number of subcomponents and/or the number of different subcomponents
• • Average size of the subcomponents, such as the average sentence length

     Ordinal features( ordered categorical (ordinal, e.g. t-shirt size would be an ordinal feature, because we can define an order XL > L > M);  unordered categorical (nominal, e.g. t-shirt color as a nominal feature ) ) allow us to perform ranking, sorting, and grouping of similar values. As we have seen in previous chapters, features can be numerical or categorical. Numerical features( continuous(e.g. house price) ) are often described as being ordinal. For example, three people, Alice, Bob and Charlie, may have heights of 1.5 m, 1.6 m and 1.7 m. We would say that Alice and Bob are more similar in height than are Alice and Charlie.

     The Adult dataset that we loaded in the last section contains examples of continuous, ordinal features. For example, the Hours-per-week feature tracks how many hours per week people work. Certain operations make sense on a feature like this. They include computing the mean, standard deviation, minimum and maximum. There is a function in pandas for giving some basic summary stats of this type:

adult['Hours-per-week'].describe()

     Some of these operations do not make sense for other features. For example, it doesn't make sense to compute the sum of the education statuses教育程度.

     There are also features that are not numerical, but still ordinal. The Education feature in the Adult dataset is an example of this. For example, a Bachelor's degree is a higher education status than finishing high school, which is a higher status than not completing high school. It doesn't quite make sense to compute the mean of these values, but we can create an approximation by taking the median value. The dataset gives a helpful feature Education-Num, which assigns a number that is basically equivalent to the number of years of education completed. This allows us to quickly compute the median:

adult['Education-Num'].median()

     The result is 10, or finishing one year past high school(刚好读完高一). If we didn't have this, we could compute the median by creating an ordering over the education values如果没有受教育年限数据，我们为不同教育阶段指定数字编号，也可以计算均值.

%matplotlib inline

import seaborn as sns
import matplotlib.pyplot as plt

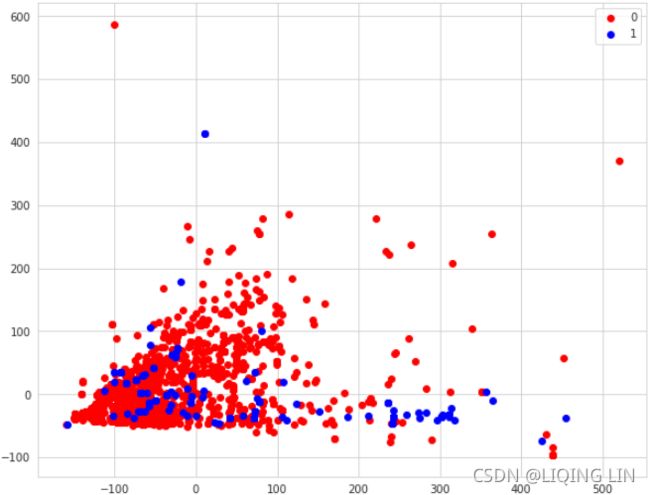
plt.figure( figsize=(12, 9) )

sns.swarmplot( x='Education-Num',
               y='Hours-per-week',
               hue='Earnings-Raw',
               data = adult[::50],
               size=12
             )

      we can create a LongHours feature, which tells us if a person works more than 40 hours per week. This turns our continuous feature (Hours-per-week) into a categorical one

    Features can also be categorical. For instance, a ball can be a tennis ball, cricket ball, football, or any other type of ball. Categorical features are also referred to as nominal features. For nominal features, the values are either the same or they are different. While we could rank balls by size or weight, just the category alone isn't enough to compare things. A tennis ball is not a cricket ball[ˈkrɪkɪt bɔːl]棒球, and it is also not a football. We could argue that a tennis ball is more similar to a cricket ball (say, in size), but the category alone doesn't differentiate this—they are the same, or they are not.

     We can convert categorical features to numerical features using the one-hot encoding, as we saw inm03 Predicting Sports Winners with Decision Trees_NBA_TP_metric_OneHotEncoder_bias_colab_Linli522362242的专栏-CSDN博客, Predicting Sports Winners with Decision Trees. For the aforementioned categories of balls, we can create three new binary features: is a tennis ball, is a cricket ball, and is a football. For a tennis ball, the vector would be [1, 0, 0]. A cricket ball has the values [0, 1, 0], while a football has the values [0, 0, 1]. These features are binary, but can be used as continuous features by many algorithms. One key reason for doing this is that it easily allows for direct numerical comparison (such as computing the distance between samples).

Mapping convert string representation(label/class/category) to integer########

https://blog.csdn.net/Linli522362242/article/details/108230328

Mapping ordinal features(size, XL>L>M)

import pandas as pd
 
df = pd.DataFrame([['green', 'M', 10.1, 'clas2'],
                   ['red', 'L', 13.5, 'class1'],
                   ['blue', 'XL', 15.3, 'class2']
                  ])
df.columns = ['color', 'size', 'price', 'classlabel']
df

Mapping ordinal features(size, XL>L>M)

size_mapping = {'XL': 3,
                'L': 2,
                'M': 1}
df['size'] = df['size'].map(size_mapping)
df

ordinal features(integer values) will not go further(use one-hot encoding)

#########Optional: Encoding Ordinal Features

     If we are unsure about the numerical differences between the categories of ordinal features, or the difference between two ordinal values is not defined, we can also encode them using a threshold encoding with 0/1 values. For example, we can split the feature "size" with values M, L, and XL into two new features "x > M" and "x > L". Let's consider the original DataFrame:

df = pd.DataFrame([['green', 'M', 10.1, 'class2'],
                   ['red', 'L', 13.5, 'class1'],
                   ['blue', 'XL', 15.3, 'class2']])
 
df.columns = ['color', 'size', 'price', 'classlabel']
df

     We can use the apply method of pandas' DataFrames to write custom lambda expressions in order to encode these variables using the value-threshold approach:

df['x > M'] = df['size'].apply( lambda x: 1 if x in {'L', 'XL'} else 0 ) #return 1 if x in {'L', 'XL'} else 0
df['x > L'] = df['size'].map( lambda x: 1 if x == 'XL' else 0 ) #return 1 if x == 'XL' else 0
 
del df['size']###
df

M: 0 0 ,  L: 1, 0 ,  XL:1, 1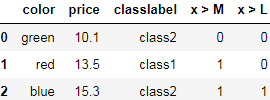
similar to a regular(dense) NumPy array
#########
     If we want to transform the integer values back to the original string representation at a later stage, we can simply define a reverse-mapping dictionary inv_size_mapping = {v: k for k, v in size_mapping.items()} that can then be used via the pandas map method on the transformed feature column, similar to the size_mapping dictionary that we used previously. We can use it as follows:

inv_size_mapping = {v: k for k,v in size_mapping.items()} # return a value(k)
df['size'].map(inv_size_mapping)

import numpy as np
# create a mapping dict
# to convert class labels from strings to integers
class_mapping = { label: idx for idx, label in 
                  enumerate( np.unique(df['classlabel']) )
                }
class_mapping

 : dict

Mapping unordered categorical (nominal)

# to convert class labels from strings to integers
df['classlabel'] = df['classlabel'].map(class_mapping)
df

These features are binary, but can be used as continuous features by many algorithms.

     We can reverse the key-value pairs in the mapping dictionary as follows to map the converted class labels(integer) back to the original string representation

inv_class_mapping = {v: k for k,v in class_mapping.items()}
df['classlabel'] = df['classlabel'].map(inv_class_mapping)
df

DataFrame get_dummies###########

columns        list-like, default None

Column names in the DataFrame to be encoded. If columns is None then all the columns with object or category dtype will be converted.(here just color, since only color value is string)

sparse        bool, default False

Whether the dummy-encoded columns should be backed by a SparseArray (True, e.g. 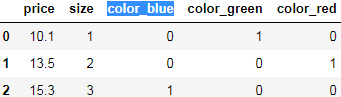) or a regular(dense) NumPy array (False, e.g.). But whether the sparse parameter is set to sparse=True or sparse=False, as long as drop_first=False(default), the returned is sparse matrix, so we don’t need to set this parameter, just set drop_first

drop_first        bool, default False(return a sparse  matrix; True: a regular(dense) NumPy array)

Whether to get k-1 dummies out of k categorical levels by removing the first level.

# one-hot encoding via pandas
pd.get_dummies( df[ ['price', 'color', 'size'] ], 
                columns = ['color']
              )

unordered categorical(nominal feature)

# multicollinearity guard in get_dummies

pd.get_dummies( df[ ['price', 'color', 'size'] ], 
                drop_first=True )

we remove the column color_blue, the feature information is still preserved since if we observe color_green=0 and color_red=0, it implies that the observation must be blue.  

1.LabelEncoder() convert string representation(label/class/category) to integer

from sklearn.preprocessing import LabelEncoder

X = df[['color', 'size', 'price']].values
# X
# array([['green', 1, 10.1],
#        ['red', 2, 13.5],
#        ['blue', 3, 15.3]], dtype=object)
color_le = LabelEncoder()
X[:,0] = color_le.fit_transform(X[:, 0])
X

 ==>unordered categorical(nominal feature )

corlor_le.inverse_transform(X[:, 0])==>
      a learning algorithm will now assume that green is larger than blue, and red is larger than green
A common workaround for this problem is to use a technique called one-hot encoding 

2.OneHotEncoder convert integer representation(label/class/category) to a sparse matrix

from sklearn.preprocessing import OneHotEncoder
X=df[['color', 'size', 'price']].values
# X
# array([['green', 1, 10.1],
#        ['red', 2, 13.5],
#        ['blue', 3, 15.3]], dtype=object)
color_ohe=OneHotEncoder()
# X[:,0] ==> array(['green', 'red', 'blue'], dtype=object)
# X[:,0].reshape(-1,1) ==>
# array([['green'],
#        ['red'],
#        ['blue']], dtype=object)
color_ohe.fit_transform( X[:,0].reshape(-1,1) ).toarray()

     When we are using one-hot encoding datasets, we have to keep in mind that it introduces multicollinearity, which can be an issue for certain methods (for instance, methods that require matrix inversion). If features are highly correlated, matrices are computationally difficult to invert, which can lead to numerically unstable estimates. To reduce the correlation among variables, we can simply remove one feature column from the one-hot encoded array. Note that we do not lose any important information by removing a feature column, though; for example, if we remove the column color_blue, the feature information is still preserved since if we observe color_green=0 and color_red=0, it implies that the observation must be blue. 

 toarray(): Numpy array                    color_ohe=OneHotEncoder(drop='first')                                                                                           color_ohe.fit_transform( X[:,0].reshape(-1,1) ).toarray()

                 These features are binary, but can be used as continuous features by many algorithms.
     When we initialized the OneHotEncoder. By default, the OneHotEncoder returns a sparse matrix when we use the transform method, and we converted the sparse matrix representation into a regular (dense) NumPy array for the purpose of visualization via the toarray method. Sparse matrices are a more efficient way of storing large datasets and one that is supported by many scikit-learn functions, which is especially useful if an array contains a lot of zeros. To omit the toarray step, we could alternatively initialize the encoder as OneHotEncoder(..., sparse=False) to return a regular NumPy array.
###
m03 Predicting Sports Winners with Decision Trees_NBA_TP_metric_OneHotEncoder_bias_colab_Linli522362242的专栏-CSDN博客

from sklearn.preprocessing import OneHotEncoder
 
onehot = OneHotEncoder()
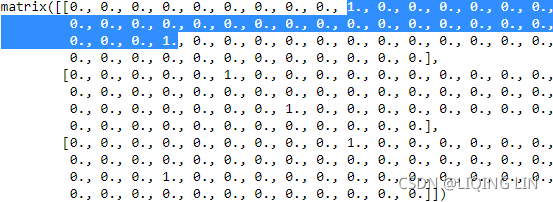
X_teams = onehot.fit_transform( X_teams ).todense()
 
X_teams[-3:]

todense(): matrix 

 ColumnTransformer process multiple columns      ########################

from sklearn.compose import ColumnTransformer
 
X = df[['color', 'size', 'price']].values
# X
# array([['green', 1, 10.1],
#        ['red', 2, 13.5],
#        ['blue', 3, 15.3]], dtype=object)
                             #( name   , transformer    , columns )
c_transf = ColumnTransformer([('onehot', OneHotEncoder(), [0]),
                              ('nothing', 'passthrough', [1,2])# 'passthrough': to pass [columns] through untransformed
                             ])                                # 'drop': to drop the [columns]
c_transf.fit_transform(X).astype(float)

                                                             color_ohe = OneHotEncoder(categories='auto',drop='first')

 VS 

 ##########

     The Adult dataset contains several categorical features, with Work-Class being one example. While we could argue that some values are of higher rank than others (for instance, a person with a job is likely to have a better income than a person without), it doesn't make sense for all values. For example, a person working for the state government is not more or less likely to have a higher income than someone working in the 私企private sector[ˈsektər]小群体；区域，部分；（经济、贸易）部门.

We can view the unique values for this feature in the dataset using the unique() function:

adult['Work-Class'].unique()

There are some missing values in the preceding dataset, but they won't affect our computations in this example.

     Similarly, we can convert numerical features to categorical features through a process called discretization[dɪs'krɪtɪ'zeʃən]离散化, as we saw in Cp4m04_Recommending Movies w Affinity Analysis_Apriori_sys.stdout.flush_df.iterrows_Sort nested dict嵌套_Linli522362242的专栏-CSDN博客, Recommending Movies Using Affiity Analysis. We can call any person who is taller than 1.7 m tall, and any person shorter than 1.7 m short. This gives us a categorical feature (although still an ordinal one). We do lose some data here. For instance, two people, one 1.69 m tall and one 1.71 m, will be in two different categories and considered drastically[ˈdræstɪkli]彻底地 different from each other. In contrast, a person 1.2 m tall will be considered "of roughly the same height" as the person 1.69 m tall! This loss of detail is a side effect of discretization, and it is an issue that we deal with when creating models.

     In the Adult dataset, we can create a LongHours feature, which tells us if a person works more than 40 hours per week. This turns our continuous feature (Hours-per-week) into a categorical one:
##############

13_Loading & Preproces Data from multiple CSV with TF 2_Feature Columns_TF eXtended_num_oov_buckets_Linli522362242的专栏-CSDN博客

Bucketized column（分桶列 )

     Often, you don’t want to feed a number directly into the model, but instead split its value into different categories based on numerical ranges. Consider raw data that represents a person’s age. Instead of representing age as a numeric column, we could split the age(continuous feature) into several buckets(categories) using a bucketized column. Notice the one-hot values below describe which age range each row matches. Buckets include the left boundary, and exclude the right boundary. For example, consider raw data that represents the year a house was built. Instead of representing that year as a scalar numeric column, we could split the year into the following four buckets:

The model will represent the buckets as follows:

     Why would you want to split a number — a perfectly valid input to your model — into a categorical value? Well, notice that the categorization splits a single input number into a four-element vector. Therefore, the model now can learn four individual weights rather than just one; four weights creates a richer model than one weight. More importantly, bucketizing enables the model to clearly distinguish between different year categories since only one of the elements is set (1) and the other three elements are cleared (0). For example, when we just use a single number (a year) as input, a linear model can only learn a linear relationship. So, bucketing provides the model with additional flexibility that the model can use to learn模型可以学习更复杂的关系.

##############

adult['LongHours'] = adult['Hours-per-week'] > 40
adult.head(n=10)

Creating good features

     Modeling, and the loss of information that the simplification causes, are the reasons why we do not have data mining methods that can just be applied to any dataset. A good data mining practitioner will have, or obtain, domain knowledge in the area they are applying data mining to. They will look at the problem, the available data, and come up with a model that represents what they are trying to achieve.

     For instance, a height feature may describe one component of a person, but may not describe their academic performance well. If we were attempting to predict a person's grade, we may not bother measuring each person's height.

     This is where data mining becomes more art than science. Extracting good features is difficult and is the topic of significant and ongoing research. Choosing better classification algorithms can improve the performance of a data mining application, but choosing better features is often a better option.

     In all data mining applications, you should first outline确定大致的方向,概述 what you are looking for before you start designing the methodology that will find it. This will dictate[ˈdɪkteɪt] 规定；影响,指示 the types of features you are aiming for, the types of algorithms that you can use, and the expectations on the final result.

Feature selection

     We will often have a large number of features to choose from, but we wish to select only a small subset. There are many possible reasons for this:

• • Reducing complexity: Many data mining algorithms need more time and resources with increase in the number of features. Reducing the number of features is a great way to make an algorithm run faster or with fewer resources.
• • Reducing noise: Adding extra features doesn't always lead to better performance. Extra features may confuse the algorithm, finding correlations and patterns that don’t have meaning (this is common in smaller datasets). Choosing only the appropriate features is a good way to reduce the chance of random correlations that have no real meaning.
• • Creating readable models: While many data mining algorithms will happily compute an answer for models with thousands of features, the results may be difficult to interpret for a human. In these cases, it may be worth using fewer features and creating a model that a human can understand.

     Some classification algorithms can handle data with issues such as these. Getting the data right and getting the features to effectively describe the dataset you are modeling can still assist algorithms.

     There are some basic tests we can perform, such as ensuring that the features are at least different. If a feature's values are all same, it can't give us extra information to perform our data mining.

     The VarianceThreshold transformer in scikit-learn, for instance, will remove any feature that doesn't have at least a minimum level of variance in the values. To show how this works, we first create a simple matrix using NumPy:

import numpy as np

X = np.arange(30).reshape( (10,3) )
X

     The result is the numbers zero to 29, in three columns and 10 rows. This represents a synthetic dataset with 10 samples and three features:

Then, we set the entire second column/feature to the value 1:

X[:,1] = 1
X

 
We can now create a VarianceThreshold transformer and apply it to our dataset:

from sklearn.feature_selection import VarianceThreshold

 ... ...

 ImportError: cannot import name '_libsvm_sparse' from 'sklearn.svm' (C:\Anaconda3\envs\tensorflow\lib\site-packages\sklearn\svm\__init__.py)

 ??????????????????

since my Scikit-Learn doesn't include feature_selection
Then go to cmd.exe, type command conda list

 So I have to use google colab:

from sklearn.feature_selection import VarianceThreshold

vt = VarianceThreshold()
Xt = vt.fit_transform(X)

Xt

threshold        float, default=0

Features with a training-set variance lower than this threshold will be removed. The default is to keep all features with non-zero variance, i.e. remove the features that have the same value in all samples.

Variances:

np.var( X, axis=0)

OR 

np.nanvar(X, axis=0)

 OR

( X.std(axis=0) )**2

  population variance
Numpy's std uses ddof=0 (population standard deviation)

cp4 Training Sets Preprocessing_StringIO_dropna_categorical_feature_Encode_Scale_L1_L2_bbox_to_ancho_Linli522362242的专栏-CSDN博客

 

sum( ( X-X.mean(axis=0) )**2 )/(X.shape[0])

 Proved==>Numpy's std uses ddof=0 (population variance ==>population standard deviation )

We can observe the variances for each column by printing the vt.variances_ attribute:

vt.variances_

  ?????

​​​​​​scikit-learn/_variance_threshold.py at 2beed55847ee70d363bdbfe14ee4401438fba057 · scikit-learn/scikit-learn · GitHub

def fit(self, X, y=None): 

        if hasattr(X, "toarray"):   # sparse matrix
            _, self.variances_ = mean_variance_axis(X, axis=0)
            if self.threshold == 0:
                mins, maxes = min_max_axis(X, axis=0)
                peak_to_peaks = maxes - mins
        else:
            self.variances_ = np.nanvar(X, axis=0)
            if self.threshold == 0:
                peak_to_peaks = np.ptp(X, axis=0)

        if self.threshold == 0:
            # Use peak-to-peak to avoid numeric precision issues
            # for constant features
            compare_arr = np.array([self.variances_, peak_to_peaks])
            self.variances_ = np.nanmin(compare_arr, axis=0)

hasattr( X, 'toarray')

  since X is not a sparse matrix == go to ==> else statement

np.nanvar(X, axis=0) == return ==> 

 np.ptp(X, axis=0) == return ==> 
numpy.ptp(a, axis=None, out=None, keepdims=)
                 Range of values (maximum - minimum) along an axis.

np.max(X, axis=0) - np.min(X,axis=0)

 

compare_arr = np.array([self.variances_, peak_to_peaks])
self.variances_ = np.nanmin(compare_arr, axis=0) ==>

      The result shows that while the first and third column contains at least some information, the second column had no variance:

     A simple and obvious test like this is always good to run when seeing data for the first time. Features with no variance do not add any value to a data mining application; however, they can slow down the performance of the algorithm.

Selecting the best individual features

     If we have a number of features, the problem of finding the best subset is a difficult task. It relates to solving the data mining problem itself, multiple times. As we saw inm04_Recommending Movies w Affinity Analysis_Apriori_sys.stdout.flush_df.iterrows_Sort nested dict嵌套_Linli522362242的专栏-CSDN博客, Recommending Movies Using Affinity Analysis, subset-based tasks increase exponentially as the number of features increase. This exponential growth in time needed is also true for finding the best subset of features. 

     A workaround to this problem is not to look for a subset that works well together, rather than just finding the best individual features. This univariate[junɪ'vɛrɪet] 单变量的 feature selection gives us a score based on how well a feature performs by itself. This is usually done for classification tasks, and we generally measure some type of correlation between a variable and the target class.

     The scikit-learn package has a number of transformers for performing univariate feature selection. They include SelectKBest, which returns the k best performing features, and SelectPercentile, which returns the top r% of features. In both cases, there are a number of methods of computing the quality of a feature.

     There are many different methods to compute how effectively a single feature correlates with a class value. A commonly used method is the chi-squared (χ2) test. Other methods include mutual information and entropy.

     We can observe single-feature tests in action using our Adult dataset. First, we extract a dataset and class values from our pandas DataFrame. We get a selection of the features:

X = adult[ ['Age', 'Education-Num', 'Capital-gain', 'Capital-loss', 
            'Hours-per-week'
           ]
         ].values
X

 
     We will also create a target class array by testing whether the Earnings-Raw value is above $50,000 or not. If it is, the class will be True. Otherwise, it will be False. Let's look at the code:

adult['Earnings-Raw'][:10], adult['Earnings-Raw'][-10:],

y = ( adult['Earnings-Raw'] == ' >50K' ).values
y[:10], y[-10:]

###############

CHAID: Humidity has 2 categories and our expected values should be evenly distributed in order to calculate how distinguishing the variable is: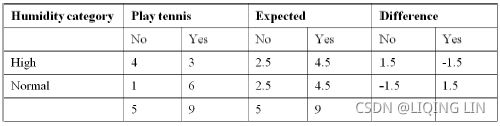

卡方检验就是统计样本的实际观测值(Play tennis)与理论推断值(Expected)之间的偏离程度(Difference)，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，如果卡方值越大，二者偏差程度越大；反之，二者偏差越小；若两个值完全相等时，卡方值就为0，表明理论值完全符合。 注意：卡方检验针对分类变量
Calculating χ2 (Chi-square卡方) value: 


Calculating degrees of freedom = (r-1) * (c-1)
Where
        r = number of row components or number of variable categories,
        c = number of response variables.
Here, there are two row categories (High and Normal) and two column categories (No and
Yes).
Hence, degrees of freedom = (r-1) * (c-1)  = (2-1) * (2-1) = 1, and 2 since ( No or Yes )
p-value for Chi-square 2.8 with 1 d.f = 0.0942
p-value can be obtained with the following Excel formulae: = CHIDIST (2.8, 1) = 0.0942

from scipy import stats

# https://www.graduatetutor.com/statistics-tutor/probability-density-function-pdf-and-cumulative-distribution-function-cdf/
pval = 1 - stats.chi2.cdf( 2.8, 1 )# Cumulative Distribution Function
pval

 
     In a similar way, we will calculate the p-value for all variables and select the best variable
with a low p-value(High Chi-square value).

###############

     Next, we create our transformer using the chi2 function and a SelectKBest transformer:

Xt_chi2 = transformer.fit_transform( X, y )
Xt_chi2

<= k=3 feature variables=

     The resulting matrix now only contains 3 features. We can also get the scores for each column, allowing us to find out which features were used. Let's look at the code:

print( transformer.scores_ )

  'Age', 'Education-Num', 'Capital-gain', 'Capital-loss',  'Hours-per-week'

 

     The highest values are for the first, third, and fourth columns Correlates to the Age, Capital-Gain, and Capital-Loss features. Based on a univariate feature selection, these are the best features to choose.

################
     我们常常把一个式子中独立变量的个数称为这个式子的“自由度”，确定一个式子自由度的方法是：若式子包含有 n 个变量，其中k 个被限制的样本统计量（常见的统计量有：样本均值，样本方差，样本极差等），则这个表达式的自由度为 n-k。比如中包含ξ1，ξ2，…，ξn这 n 个变量，其中ξ1-ξn-1相互独立，ξn为其余变量的平均值，因此自由度为 n-1。

from scipy import stats
                                         # 2 : >50K or not
# degrees of freedom =(r-1)(2-1) =r-1 = Xt.shape[1]-1
pval = 1-stats.chi2.cdf( transformer.scores_, X.shape[1]-1 )
pval

 

transformer.pvalues_

 There is no doubt that you cannot use pvalue because the pvalue here is all 0.
################

     If you'd like to find out more about the features in the Adult dataset, take a look at the adult.names file that comes with the dataset and the academic paper it references.
Index of /ml/machine-learning-databases/adult

     We could also implement other correlations, such as the Pearson's correlation coefficient. This is implemented in SciPy, a library used for scientific computing (scikit-learn uses it as a base).
#######################################
cp10_回归预测连续目标变量_boston_Residual_plot_mlxtend_sns_pd_covariance_correlation_RANSAC_R2_Ridge_C_F_A_K_树_Linli522362242的专栏-CSDN博客

     In the previous section, we visualized the data distributions of the Housing dataset variables in the form of histograms and scatterplots. Next, we will create a correlation matrix to quantify量化 and summarize linear relationships between variables https://blog.csdn.net/Linli522362242/article/details/103387527. A correlation matrix is closely related to the covariance matrix that we covered in the section Unsupervised dimensionality reduction via principal component analysis in cp5_Compressing Data via Dimensionality Reduction_feature extraction_PCA_LDA_convergence_kernel PCA https://blog.csdn.net/Linli522362242/article/details/105196037.

constructing the covariance matrix

     The symmetric d × d -dimensional covariance matrix, where d is the number of dimensions in the dataset, stores the pairwise成对地 covariances between the different features. For example, the covariance between two features  and on the population level can be calculated via the following equation:
 VS  sample covariances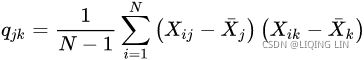 
     The reason the sample covariance matrix has N-1 in the denominator rather than N is essentially that the population mean(OR u) is not known and is replaced by the sample mean . 
     Here,  and  are the sample means of feature j and k , respectively. Note that the sample means are zero if we standardize the datasetcp4 Training Sets Preprocessing_StringIO_dropna_categorical_feature_Encode_Scale_L1_L2_bbox_to_ancho_Linli522362242的专栏-CSDN博客. A positive covariance between two features indicates that the features increase or decrease together, whereas a negative covariance indicates that the features vary in opposite directions. For example, a covariance matrix of three features can then be written as (note that  stands for the Greek uppercase letter sigma, which is not to be confused with the sum symbol):

     We can interpret the correlation matrix as being a rescaled version of the covariance matrix. In fact, the correlation matrix is identical to a covariance matrix computed from standardized features.

     The correlation matrix相关系数矩阵 is a square matrix that contains the Pearson product-moment correlation coefficient 皮尔逊积矩相关系数 (often abbreviated as Pearson's r), which measures the linear dependence between pairs of features. The correlation coefficients are in the range –1 to 1. Two features have a perfect positive correlation if r = 1, no correlation if r = 0, and a perfect negative correlation if r = –1. As mentioned previously, Pearson's correlation coefficient can simply be calculated as the covariance between two features, x and y (numerator), divided by the product of their standard deviations (denominator):
( Pearson product-moment correlation coefficient )Pearson's r :  

Covariance versus correlation for standardized features

     We can show that the covariance between a pair of standardized features is, in fact, equal to their linear correlation coefficient. To show this, let's first standardize the features x and y to obtain their z-scores, which we will denote as ′ and ′, respectively: 
     Remember that we compute the (population) covariance between two features as follows: 
     Since standardization centers a feature variable at mean zero, we can now calculate the covariance between the scaled features as follows: 

     Through re-substitution( ), we then get the following result:<==

Finally, we can simplify this equation as follows: ( correlation coefficient formula)
#######################################

First, we import the pearsonr function from SciPy:

scipy.stats.pearsonr — SciPy v1.7.1 Manual

scipy.stats.pearsonr(x, y)

     Pearson correlation coefficient and p-value for testing non-correlation.

     The Pearson correlation coefficient measures the linear relationship between two datasets. The calculation of the p-value(float, Two-tailed p-value.) relies on the assumption that each dataset is normally distributed. (See Kowalski [3] for a discussion of the effects of non-normality of the input on the distribution of the correlation coefficient.) Like other correlation coefficients, this one varies between -1 and +1 with 0 implying no correlation. Correlations of -1 or +1 imply an exact linear relationship. Positive correlations imply that as x increases, so does y. Negative correlations imply that as x increases, y decreases.

The p-value roughly indicates the probability of an uncorrelated system producing datasets that have a Pearson correlation at least as extreme as the one computed from these datasets.

from scipy.stats import pearsonr

     The preceding function(pearsonr) almost fits the interface needed to be used in scikit-learn's univariate单变量的 transformers. The function needs to accept two arrays (x and y in our example) as parameters and returns two arrays, the scores for each feature and the corresponding p-values. The chi2 function we used earlier only uses the required interface, which allowed us to just pass it directly to SelectKBest.

     The pearsonr function in SciPy accepts two arrays; however, the X array it accepts is only one dimension. We will write a wrapper function that allows us to use this for multivariate arrays like the one we have. Let's look at the code:

def multivariate_personr(X, y):
    scores, pvalues = [], [] # each score: Pearson's correlation coefficient
    for feature_index in range( X.shape[1] ):
      cur_score, cur_p = pearsonr( X[:, feature_index], y)
      scores.append( abs(cur_score) )
      pvalues.append( cur_p )

    return ( np.array(scores), np.array(pvalues) ) 

     The Pearson value could be between -1 and 1. A value of 1 implies a perfect correlation between two variables, while a value of -1 implies a perfect negative correlation, that is, high values in one variable give low values in the other and vice versa. Such features are really useful to have, but would be discarded. For this reason, we have stored the absolute value in the scores array, rather than the original signed value.

     Now, we can use the transformer class as before to rank the features using the Pearson correlation coefficient: 

transformer = SelectKBest( score_func = multivariate_personr, k=3 )
Xt_pearson = transformer.fit_transform( X,y )
print( transformer.scores_ )

  'Age', 'Education-Num', 'Capital-gain', 'Capital-loss',  'Hours-per-week'

      This returns a different set of features! The features chosen this way are the first, second, and fifth columns: the Age, Education, and Hours-per-week worked. This shows that there is not a definitive answer to what the best features are— it depends on the metric.

np.hstack( (X,y[..., np.newaxis]) )

 
cp10_回归预测连续目标变量_boston_Residual_plot_mlxtend_sns_pd_covariance_correlation_RANSAC_R2_Ridge_C_F_A_K_树_Linli522362242的专栏-CSDN博客

import seaborn as sns
import numpy as np
import matplotlib
matplotlib.rcParams.update(matplotlib.rcParamsDefault)

features=['Age', 'Education-Num', 'Capital-gain', 'Capital-loss', 'Hours-per-week',
          'Earnings-Raw' # target class
         ]


font = {'size': 15,}

sns.set(font_scale=1.2)

# https://blog.csdn.net/ztf312/article/details/102474190
cm = np.corrcoef( np.hstack( (X,y[..., np.newaxis]) ).T )# adult[features].values.T : (n_instances, n_features) ==> (n_features, n_instances)
mask = np.zeros_like(cm)
mask[np.triu_indices_from(mask)] = True
hm = sns.heatmap( cm,
                  cmap='Purples',
                  mask=mask,
                  annot=True, # If True, write the data value in each cell
                  xticklabels=features,
                  yticklabels=features
                )
plt.xticks( rotation=45 )
plt.title('Pearson correlation coefficient', fontdict=font)

plt.show()

     We can see which feature set is better by running them through a classifier. Keep in mind that the results only indicate which subset is better for a particular classifier and/or feature combination—there is rarely a case in data mining where one method is strictly better than another in all cases! Let's look at the code:

from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_val_score

clf = DecisionTreeClassifier( random_state=14 )
scores_chi2 = cross_val_score( clf, 
                               Xt_chi2, y,
                               scoring='accuracy'
                             )
scores_pearson = cross_val_score( clf, 
                                 Xt_pearson, y,
                                 scoring='accuracy'
                               )

print( "Chi2 performance: {0:.3f}".format( 
            scores_chi2.mean() 
          ) 
     )
print( "Pearson performance: {0:.3f}".format( 
            scores_pearson.mean() 
          )
     )

         The chi2 average here is 0.83, while the Pearson score is lower at 0.77. For this combination, chi2 returns better results!

     It is worth remembering the goal of this data mining activity: predicting wealth. Using a combination of good features and feature selection, we can achieve 83 percent accuracy using just three features of a person!

Feature creation

     Sometimes, just selecting features from what we have isn't enough. We can create features in different ways from features we already have. The one-hot encoding method we saw previously is an example of this. Instead of having a category features with options A, B and C, we would create three new features Is it A?, Is it B?, Is it C?.

     Creating new features may seem unnecessary and to have no clear benefit—after all, the information is already in the dataset and we just need to use it. However, some algorithms struggle when features correlate significantly, or if there are redundant features特征之间相关性很强，或者特征冗余. They may also struggle if there are redundant features.

     For this reason, there are various ways to create new features from the features we already have.

     We are going to load a new dataset, so now is a good time to start a new IPython Notebook. Download the Advertisements dataset from http://archive.ics.uci.edu/ml/datasets/Internet+Advertisements and save it to your Data folder.

Data Set Information:

This dataset represents a set of possible advertisements on Internet pages. The features encode the geometry of the image (if available) as well as phrases occuring in the URL, the image's URL and alt text, the anchor text, and words occuring near the anchor text. The task is to predict whether an image is an advertisement ("ad") or not ("nonad").

     Next, we need to load the dataset with pandas. First, we set the data's filename as always:

import pandas as pd

url_ads = 'http://archive.ics.uci.edu/ml/machine-learning-databases/internet_ads/ad.data'

ads = pd.read_csv( url_ads, # or 'adult.data',
                   sep=',',
                   keep_default_na=False,
                   header=None,
                 )

ads.dtypes

  and 

converters        dict, optional

     Dict of functions for converting values in certain columns. Keys can either be integers or column labels.

pandas.read_csv — pandas 1.3.3 documentation

     There are a couple of issues with this dataset that stop us from loading it easily. First, the first few features are numerical, but pandas will load them as strings. To fix this, we need to write a converting function that will convert strings to numbers if possible. Otherwise, we will get a NaN (which is short for Not a Number), which is a special value that indicates that the value could not be interpreted as a number. It is similar to none or null in other programming languages.

     we want to set the final column (column index #1558), which is the class, to a binary feature. In the Adult dataset, we created a new feature for this. In the dataset, we will convert the feature while we load it.

import pandas as pd
import numpy as np

url_ads = 'http://archive.ics.uci.edu/ml/machine-learning-databases/internet_ads/ad.data'

def convert_number(x):
  try:
      return float(x)
  except ValueError:
      return np.nan

converters = {}
for i in range( 1558 ):# column_index=1558 : 'ad' or 'nonad'
  converters[i] = convert_number

converters[1558] = lambda x: 1 if x.strip() == 'ad.' else 0

ads = pd.read_csv( url_ads, # or 'adult.data',
                   sep=',',
                   keep_default_na=False,
                   header=None,
                   converters=converters
                 )

ads.head()

 The resulting dataset is quite large, with 1,559 features and 3,279 rows. Here are some of the feature values the first five, printed by inserting ads[:5] into a new cell:

ads.shape

 

ads.dropna( inplace=True )

 

ads.shape

     This dataset describes images on websites, with the goal of determining whether a given image is an advertisement or not.

     The features in this dataset are not described well by their headings. There are two files accompanying the ad.data file that have more information: ad.DOCUMENTATION and ad.names. The first three features are the height, width, and ratio of the image size宽高比. The final feature is 1 if it is an advertisement and 0 if it is not. 

     The other features are 1 for the presence of certain words in the URL, alt text, or caption of the image图像标题. These words, such as the word sponsor赞助商, are used to determine if the image is likely to be an advertisement. Many of the features overlap considerably, as they are combinations of other features. Therefore, this dataset has a lot of redundant information.

     With our dataset loaded in pandas, we will now extract the x and y data for our classification algorithms. The x matrix will be all of the columns in our Dataframe, except for the last column. In contrast, the y array will be only that last column, feature #1558. Let's look at the code:

X = ads.drop(1558, axis=1).values
y = ads[1558]

Principal Component Analysis

     In some datasets, features heavily correlate with each other. For example, the speed and the fuel consumption燃油消耗 would be heavily correlated in a go-kart with a single gear有1个档的微型单座赛车. While it can be useful to find these correlations for some applications, data mining algorithms typically do not need the redundant information.

     The ads dataset has heavily correlated features, as many of the keywords are repeated across the alt text and caption.

     The Principal Component Analysis (PCA) aims to find combinations of features that describe the dataset in less information. It aims to discover principal components, which are features that do not correlate with each other and explain the information—specifically the variance—of the dataset. What this means is that we can often capture most of the information in a dataset in fewer features.

############################################################################

The main steps behind principal component analysis

      In this section, we will discuss PCA (Principal Component Analysis), an unsupervised linear transformation technique that is widely used across different fields, most prominently for feature extraction and dimensionality reduction. Other popular applications of PCA include
exploratory data analyses and de-noising去噪 of signals in stock market trading, and the analysis of genome data and gene expression levels in the field of bioinformatics生物信息学.
     PCA helps us to identify patterns in data based on the correlation between features. In a nutshell简言之, PCA aims to find the directions of maximum variance in highdimensional data and projects it onto a new subspace with equal or fewer dimensions than the original one(PCA identifies the hyperplane that lies closest to the data, and then it projects the data onto it.). The orthogonal axes (principal components) of the new subspace can be interpreted as the directions of maximum variance given the constraint that the new feature axes are orthogonal to each other, as illustrated in the following figure:
Here,  and  are the original feature axes, and PC1 and PC2 are the principal components.

Preserving the Variance保留（最大）方差

Figure 8-7. Selecting the subspace onto which to project

     Before you can project the training set onto a lower-dimensional hyperplane, you first need to choose the right hyperplane. For example, a simple 2D dataset is represented on the left of Figure 8-7, along with three different axes (i.e., one-dimensional hyperplanes). On the right is the result of the projection of the dataset onto each of these axes. As you can see, the projection onto the solid line preserves the maximum variance, while the projection onto the dotted line preserves very little variance, and the projection onto the dashed line preserves an intermediate amount of variance. variance measures the spread of values along a feature axis(variance measures值沿特征轴的分布).

正交矩阵

     正交矩阵是在欧几里得空间里的叫法，在酉空间里叫酉矩阵，一个正交矩阵对应的变换叫正交变换，这个变换的特点是不改变向量的尺寸和向量间的夹角，那么它到底是个什么样的变换呢？看下面这张图
假设二维空间中的一个向量OA，它在标准坐标系即向量e1、e2所在的坐标轴，坐标矩阵是=[a,b]'（用'表示转置），现在把它用另一组向量e1'、e2'表示为=[a',b']'，存在矩阵U使得[a',b']'=U([a,b]')，则U即为正交矩阵。从图中可以看到，正交变换只是将变换向量用另一组正交基表示，在这个过程中并没有对向量OA做拉伸，也不改变向量OA的空间位置，加入两个向量同时做正交变换，那么变换前后这两个向量的夹角显然不会改变。上面的例子只是正交变换的一个方面，即旋转变换，可以把e1'、e2'坐标系看做是e1、e2坐标系经过旋转某个斯塔角度得到，怎么样得到该旋转矩阵U呢？如下
向量OA：

•   OR || ||= ||x|| * ||e1'|| * cosB   角度B是向量OA和单位向量的夹角
• OR ||||= ||x|| * ||e2'|| * cosC   角度C是向量OA和单位向量的夹角 

 a'和b'实际上是x在e1'和e2'轴上的投影大小，所以直接做内积dot可得，then

从图中可以看到 单位向量(模等于1的向量)和单位向量 用向量e1、e2所在的坐标轴表示
 
所以

     正交矩阵U行（列）向量之间都是单位正交向量。上面求得的是一个旋转矩阵，它对向量做旋转变换！向量OA空间位置空间位置不变是绝对的，但是坐标是相对的，假如你站在e1上看OA，随着e1旋转到e1'，看OA的相对位置就会改变。

import matplotlib.pyplot as plt
import numpy as np
 
angle = np.pi/5
stretch = 5
m = 200

# create dataset 
np.random.seed(3)
X = np.random.randn(m,2) /10 #randn: "n" is short for normal distribution
X = X.dot( np.array([ [stretch,0], 
                       [0,1]
                    ]
                   )
         ) #stretch

# Orthogonal matrix U         
X = X.dot([ [np.cos(angle), np.sin(angle)], 
            [-np.sin(angle), np.cos(angle)] 
          ]) # rotate
 
u1 = np.array([ np.cos(angle), np.sin(angle) ]) # c1
u2 = np.array([ np.cos(angle-2*np.pi/6), np.sin(angle-2*np.pi/6) ])
u3 = np.array([ np.cos(angle-np.pi/2), np.sin(angle-np.pi/2) ]) # c2

# X.dot(e1') 
X_proj1 = X.dot( u1.reshape(-1,1) ) # u1.reshape(-1,1) hidden: u1.T Tranpose
X_proj2 = X.dot( u2.reshape(-1,1) )
# X.dot(e2')
X_proj3 = X.dot( u3.reshape(-1,1) )
 
plt.figure( figsize=(10,5) )
 
# shape : sequence of 2 ints  ~  (3,2)
#        Shape of grid in which to place axis.
#        First entry is number of rows, second entry is number of columns.
# loc : sequence of 2 ints ~  (0,0)
#        Location to place axis within grid.
#        First entry is row number, second entry is column number.
plt.subplot2grid( (3,2), (0,0), rowspan=3 )
# c1
plt.plot( [-1.4, 1.4], 
          [ -1.4*u1[1]/u1[0], 1.4*u1[1]/u1[0] ], 
          "b-", linewidth=1 
        )
#
plt.plot( [-1.4, 1.4],
          [ -1.4*u2[1]/u2[0], 1.4*u2[1]/u2[0] ], 
          "g--", linewidth=1
        )
# c2
plt.plot( [-1.4, 1.4], 
          [ -1.4*u3[1]/u3[0], 1.4*u3[1]/u3[0] ], 
          "k:", linewidth=2
        )
plt.plot( X[:,0], X[:,1], "bo", alpha=0.5 )
plt.axis([ -1.4,1.4, -1.4,1.4 ])
plt.arrow( 0,0, u1[0],u1[1], 
          head_width=0.1, linewidth=5, length_includes_head=True, head_length=0.1, 
          fc="k", ec="k")
plt.arrow( 0,0, u3[0],u3[1], 
          head_width=0.1, linewidth=5, length_includes_head=True, head_length=0.1,
          fc="k", ec="k")
plt.text( u1[0]+0.1, u1[1]-0.05, 
          r"$\mathbf{c_1}$", fontsize=22 )
plt.text( u3[0]+0.1, u3[1], 
          r"$\mathbf{c_2}$", fontsize=22 )
plt.xlabel( "$x_1$", fontsize=18 )
plt.ylabel( "$x_2$", fontsize=18, rotation=0 )
plt.grid(True)
 
plt.subplot2grid( (3,2), (0,1) )
plt.plot( [-2,2], [0,0], "b-", linewidth=1 )
plt.plot( X_proj1[:,0], np.zeros(m), "bo", alpha=0.3 )
#plt.gca().get_yaxis().set_ticks([])
plt.gca().get_xaxis().set_ticklabels([])
plt.axis([-2,2, -1,1])
plt.grid(True)
 
plt.subplot2grid( (3,2), (1,1) )
plt.plot( [-2,2], [0,0], "g--", linewidth=1 )
plt.plot( X_proj2[:,0], np.zeros(m), "bo", alpha=0.3 )
plt.gca().get_yaxis().set_ticks([])
plt.gca().get_xaxis().set_ticklabels([])
plt.axis([-2,2,-1,1])
plt.grid(True)
 
plt.subplot2grid( (3,2), (2,1))
plt.plot( [-2,2], [0,0], "k:", linewidth=2 )
plt.plot( X_proj3[:,0], np.zeros(m), "bo", alpha=0.3 )
plt.gca().get_yaxis().set_ticks([])
#plt.gca().get_xaxis().set_ticklabels([])
plt.axis([-2,2,-1,1])
plt.xlabel("$z_1$", fontsize=18)
plt.grid(True)
 
plt.show()

 Figure 8-7. Selecting the subspace onto which to project

      It seems reasonable to select the axis that preserves the maximum amount of variance(more spread along the selected axis), as it will most likely lose less information than the other projections. Another way to justify this choice is that it is the axis that minimizes the mean squared distance between the original dataset and its projection onto that axis. This is the rather simple idea behind PCA.

################################
NOTE
     The direction of the principal components is not stable: if you perturb打乱 the training set slightly and run PCA again, some of the new PCs(Principal Components) may point in the opposite direction of the original PCs. However, they will generally still lie on the same axes. In some cases, a pair of PCs may even rotate or swap, but the plane they define will generally remain the same.
################################

     If we use PCA for dimensionality reduction, we construct a –dimensional transformation matrix W that allows us to map a sample vector x onto a new k–dimensional feature subspace that has fewer dimensions than the original d–dimensional feature space(k

 

 

      As a result of transforming the original d-dimensional data onto this new k-dimensional subspace (typically k << d), the first principal component will have the largest possible variance, and all consequent principal components will have the largest variance given the constraint that these components are uncorrelated (orthogonal) to the other principal components—even if the input features are correlated, the resulting principal components will be mutually orthogonal (uncorrelated). Note that the PCA directions are highly sensitive to data scaling, and we need to standardize the features prior to PCA if the features were measured on different scales and we want to assign equal importance to all features.

     Before looking at the PCA algorithm for dimensionality reduction in more detail, let's summarize the approach in a few simple steps:

1. Standardize the d-dimensional dataset.
2. Construct the covariance matrix A(dxd).
3. Decompose分解 the covariance matrix into its eigenvectors and eigenvalues.
4. Sort the eigenvalues by decreasing order to rank the corresponding eigenvectors.
5. Select k eigenvectors which correspond to the k largest eigenvalues, where k is the dimensionality of the new feature subspace ( ).
6.  Construct a projection matrix W from the "top" k eigenvectors.
7. Transform the d-dimensional input dataset X using the projection matrix W to obtain the new k-dimensional feature subspace.

################################08_Dimensionality Reduction_svd_Kernel_pca_make_swiss_roll_subplot2grid_IncrementalPCA_memmap_LLE_Linli522362242的专栏-CSDN博客

#####################

Eigenvectors and eigenvalues

     Eigenvectors and eigenvalues have significant importance in the field of linear algebra, physics, mechanics, and so on. Refreshing, basics on eigenvectors and eigenvalues is necessary when studying PCAs. Eigenvectors  are the axes (directions) along which a linear transformation acts simply by stretching/compressing and/or flipping; whereas, eigenvalues λ give you the factors by which the compression occurs. In another way, an eigenvector of a linear transformation is a nonzero vector whose direction does not change when that linear transformation is applied to it.

      More formally, A is a linear transformation from a vector space and  is a nonzero vector, then eigen vector of A if  is a scalar multiple of . The condition can be written as the following equation:

     In the preceding equation, is an eigenvector, A is a square matrix, and λ is a scalar called an eigenvalue. The direction of an eigenvector remains the same after it has been transformed by A; only its magnitude has changed, as indicated by the eigenvalue λ, That is, multiplying a matrix by one of its eigenvectors is equal to scaling the eigenvector, which is a compact representation of the original matrix. The following graph describes eigenvectors and eigenvalues in a graphical representation in a 2D space:

     The following example describes how to calculate eigenvectors and eigenvalues from the square matrix and its understanding. Note that eigenvectors and eigenvalues can be calculated only for square matrices (those with the same dimensions of rows and columns).

     Recall the equation that the product of A and any eigenvector of A must be equal to the eigenvector multiplied by the magnitude of eigenvalue:
==>
     A characteristic equation特征方程 states that the determinant行列式 of the matrix, that is the difference between the data matrix and the product of the identity matrix单位矩阵 and an eigenvalue is 0.

     Both eigenvalues λ for the preceding matrix are equal to -2. We can use eigenvalues λ to substitute for eigenvectors in an equation:

     Substituting the value of eigenvalue in the preceding equation, we will obtain the following formula:

 The preceding equation can be rewritten as a system of equations, as follows:

      This equation indicates it can have multiple solutions of eigenvectors we can substitute with any values which hold the preceding equation for verification of equation. Here, we have used the vector [1 1] for verification, which seems to be proved.

      PCA needs unit eigenvectors to be used in calculations, hence we need to divide the same with the norm or we need to normalize the eigenvector. The 2-norm equation is shown as follows:
The norm of the output vector is calculated as follows:
The unit eigenvector is shown as follows:

 #####################

1. 回顾特征值和特征向量

我们首先回顾下特征值和特征向量的定义如下：Ax=λx   (hidden: ==>左乘x' ==> A = x'λx)

• 其中A是一个n×n的实对称矩阵(如果有n阶矩阵A，其矩阵的元素都为实数，且矩阵A的转置等于其本身（aij=aji），(i,j为元素的脚标），则称A为实对称矩阵。)
  •  实对称矩阵A的不同特征值对应的特征向量是正交的。
  • 实对称矩阵A的特征值都是实数。
  • n阶实对称矩阵A必可相似对角化，且相似对角阵上的元素即为矩阵本身特征值。
  • 若A具有k重特征值λ　必有k个线性无关的特征向量，或者说秩r(λE-A)必为n-k，其中E为单位矩阵。
  • 实对称矩阵A一定可正交相似对角化。
  •   
• x是一个n维向量，则我们说λ是矩阵A的一个特征值，而x 是 矩阵A 的 特征值λ 所对应的特征向量.

　　　　求出特征值和特征向量有什么好处呢？ 就是我们可以将矩阵A特征分解。如果我们求出了矩阵A的n个特征值 λ1 ≤ λ2 ≤...≤ λn,以及这n个特征值所对应的特征向量{w1,w2,...wn} ,注意 wi是n维的 ，如果这n个特征向量线性无关，那么矩阵A就可以用下式的特征分解表示：

　　　　其中W是这n个特征向量{w1,w2,...wn}所张成的n×n维矩阵，而Σ为这n个特征值为主对角线的n×n维矩阵。

　　　　一般我们会把W的这n个特征向量标准化，即满足, 或者说，此时W的n个特征向量为标准正交基，满足，即, 也就是说W为酉矩阵。

 这样我们的特征分解表达式可以写成 

 　　　　注意到要进行特征分解，矩阵A必须为方阵。那么如果A不是方阵，即行和列不相同时，我们还可以对矩阵进行分解吗？答案是可以，此时我们的SVD登场了。

2.  SVD的定义                        奇异值分解(singular value decomposition)

      SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m×n的矩阵，那么我们定义矩阵A的SVD为：

•  其中U是一个m×m的矩阵，
• Σ是一个m×n的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值，
• V是一个n×n的矩阵。
• U和V都是酉矩阵，即满足。下图可以很形象的看出上面SVD的定义：

 那么我们如何求出SVD分解后的U,Σ,V这三个矩阵呢？

•      如果我们将A的转置和A做矩阵乘法，那么会得到n×n的一个方阵(nxm * mxn=nxn维矩阵)。既然是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式： (similar to Ax=λx)
       这样我们就可以得到矩阵的n个特征值和对应的n个特征向量了。将的所有特征向量组成一个n×n的矩阵V，就是我们SVD公式里面的V矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。

•       如果我们将A和A的转置做矩阵乘法，那么会得到m×m的一个方阵（mxn * nxm = mxm维矩阵）。既然是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：
  　  这样我们就可以得到矩阵的m个特征值和对应的m个特征向量了。将的所有特征向量组成一个m×m的矩阵U，就是我们SVD公式里面的U矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量。 

     U和V我们都求出来了，现在就剩下奇异值矩阵Σ没有求出了。由于Σ除了对角线上是奇异值其他位置都是0，那我们只需要求出每个奇异值σ就可以了。

 我们注意到: 

这样我们可以求出我们的每个奇异值，进而求出奇异值矩阵Σ。

     上面还有一个问题没有讲，就是我们说的特征向量组成的就是我们SVD中的V矩阵，而的特征向量组成的就是我们SVD中的U矩阵，这有什么根据吗？这个其实很容易证明，我们以V矩阵的证明为例。

      上式证明使用了:。可以看出的特征向量组成的的确就是我们SVD中的V矩阵(hidden: Ax=λx ==> x 是 矩阵A 的 特征值λ 所对应的特征向量 ==>左乘x' ==> A = x'λx  )。类似的方法可以得到的特征向量组成的就是我们SVD中的U矩阵

　　进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵Σ的平方，也就是说特征值和奇异值满足如下关系：==>=          ( and )

==>

　　这样也就是说，我们可以不用(<==)来计算奇异值，也可以通过求出的特征值取平方根来求奇异值。

3. SVD计算举例

进而求出的特征值和特征向量：
特征向量标准化

 

 特征值取平方根来求奇异值==>, 

 

接着求的特征值和特征向量：过程与求出的特征值和特征向量类似：

 

 ################################

     So how can you find the principal components of a training set? Luckily, there is a standard matrix factorization因数分解 technique called Singular Value Decomposition (SVD)奇异值分解 that can decompose the training set matrix X into the dot product of three matrices  where  contains all the principal components that we are looking for, as shown in Equation 8-1.
Equation 8-1. Principal components matrix

      The following Python code uses NumPy’s svd() function to obtain all the principal components of the training set, then extracts the first two PCs:

# create a dataset 

import numpy as np
 
np.random.seed(4)
m=60
w1, w2 = 0.1, 0.3
noise = 0.1

# create a dataset 
angles = np.random.rand(m) * 3 * np.pi/2 -0.5
X = np.empty((m,3)) # (number of instance, 3 dimensions)
X[:,0] = np.cos(angles) + np.sin(angles)/2 + noise*np.random.randn(m)/2
X[:,1] = np.sin(angles)*0.7 + noise*np.random.randn(m)/2
X[:,2] = X[:,0]*w1 + X[:,1]*w2 + noise*np.random.randn(m)

X_centered = X - X.mean(axis=0) ###############
U, s, Vt = np.linalg.svd(X_centered) #Vt contains all the principal components#############
c1 = Vt.T[:,0]                       #s contains all singular values
c2 = Vt.T[:,1]

##########################
WARNING
     PCA assumes that the dataset is centered around the origin. As we will see, Scikit-Learn’s PCA classes take care of centering the data for you. However, if you implement PCA yourself (as in the preceding example), or if you use other libraries, don’t forget to center the data first.
########################## 
s==>  via  S[:n,:n]=np.diag(s)

m,n = X.shape
 
S = np.zeros(X_centered.shape) #shape(60,3)=(m,3)
#np.diag(s) # np.diag(s)==array([[6.77645005, 0., 0.],
#                                [0., 2.82403671, 0.],m,n = X.shape
#                                [0., 0., 0.78116597] ])  
S[:n,:n]=np.diag(s) # np.diag(s)==array([ [6.77645005, 0., 0.], [0., 2.82403671, 0.], [0., 0., 0.78116597] ])
S[:5]

 

      PCA assumes that the dataset is centered around the origin,  and Singular Value Decomposition (SVD) that can decompose the training set matrix X into the dot product of three matrices , where  contains all the principal components that we are looking for.

np.allclose( X_centered, U.dot(S).dot(Vt) )

  # means  X_centered is equal to  U.dot(S).dot(Vt)

Projecting Down to d Dimensions

     Once you have identified all the principal components, you can reduce the dimensionality of the dataset down to d dimensions by projecting it onto the hyperplane defined by the first d principal components. Selecting this hyperplane ensures that the projection will preserve as much variance as possible. For example, in Figure 8-2 the 3D dataset is projected down to the 2D plane defined by the first two principal components, preserving a large part of the dataset’s variance. As a result, the 2D projection looks very much like the original 3D dataset.
  --> 
     To project the training set onto the hyperplane, you can simply compute the dot product of the training set matrix X by the matrix , defined as the matrix containing the first d principal components (i.e., the matrix composed of the first d columns of ), as shown in Equation 8-2.
Equation 8-2. Projecting the training set down to d dimensions
         #W2 = Vt.T[:, :2]
     The following Python code projects the training set onto the plane defined by the first two principal components:

W2 = Vt.T[:,:2]
X2D = X_centered.dot(W2)

X2D_using_svd = X2D

      There you have it! You now know how to reduce the dimensionality of any dataset down to any number of dimensions, while preserving as much variance as possible.

Using Scikit-Learn PCA

     Scikit-Learn’s PCA class implements PCA using SVD decomposition just like we did before. The following code applies PCA to reduce the dimensionality of the dataset down to 2 dimensions (note that it automatically takes care of centering the data):

from sklearn.decomposition import PCA
 
pca = PCA( n_components=2 )
X2D = pca.fit_transform(X)
X2D[:5]

X2D_using_svd[:5]  # X2D_using_svd = X_centered.dot( Vt.T[:,:2] )

 
     Notice that running PCA multiple times on slightly different datasets may result in different results. In general the only difference is that some axes may be flipped. In this example, PCA using Scikit-Learn gives the same projection as the one given by the SVD approach, except both axes as flipped:

np.allclose( X2D, -X2D_using_svd )

Recover the 3D points projected on the plane (PCA 2D subspace).           #reconstruction
Scikit-Learn's PCA class automatically takes care of reversing the mean centering

X3D_inv = pca.inverse_transform(X2D)
np.allclose(X3D_inv, X)

                        # there was some loss of information during the projection step, so the recovered 3D points are not exactly equal to the original 3D points
We can compute the reconstruction error:

np.mean( np.sum(np.square(X3D_inv-X), axis=1) )

 

                                                                                                       #reconstruction
The inverse transform in the SVD approach looks like this:   #X2D_using_svd =                                                                                                                             #W2 = Vt.T[:,:2]

# X= X2D_using_svd.dot(W2^T) => X2D_using_svd.dot(Vt[:2,:])
note: the following code does not take care of  reversing the mean centering

X3D_inv_using_svd = X2D_using_svd.dot(Vt[:2,:])  # X2D_using_svd = X_centered.dot( Vt.T[:,:2] )

      The reconstructions from both methods(The inverse transform in the SVD approach and Scikit-Learn's PCA) are not identical because Scikit-Learn's PCA class automatically takes care of reversing the mean centering, but if we subtract the mean ( from the inverse transform in the Scikit-Learn's PCA), we get the same reconstruction:

np.allclose( X3D_inv_using_svd, X3D_inv-pca.mean_ )

pca.mean_

 

round(X[:,0].mean(),8), round(X[:,1].mean(),8), round(X[:,2].mean(),8)

 

 The PCA object gives access to the principal components that it computed:

pca.components_

 the matrix , defined as the matrix containing the first d principal components (i.e., the matrix composed of the first d columns of 

W2.T # W2 = Vt.T[:,:2]

 

Compare to the first two principal components computed using the SVD method:

# U, s, Vt = np.linalg.svd(X_centered) #Vt contains all the principal components#############
Vt[:2]

 #  Notice how the axes are flipped.

 ############################################################################

     We apply PCA to ads dataset just like any other transformer. It has one key parameter, which is the number of components to find. By default, it will result in as many features as you have in the original dataset. However, these principal components are ranked—the first feature explains the largest amount of the variance in the dataset, the second a little less, and so on. Therefore, finding just the first few features is often enough to explain much of the dataset. Let's look at the code:

from sklearn.decomposition import PCA

pca = PCA( n_components=5 )
Xd = pca.fit_transform(X)

     The resulting matrix, Xd, has just 5 features. However, let's look at the amount of variance that is explained by each of these features: 

Xd.shape

 

Explained Variance Ratio

     Another very useful piece of information is the explained variance ratio(方差解释比率或者方差贡献率) of each principal component, available via the explained_variance_ratio_ variable. It indicates the proportion of the dataset’s variance that lies along the axis of each principal component.

np.set_printoptions( precision=3, suppress=True )
pca.explained_variance_ratio_

 shows us that the first feature accounts for 85.4 percent of the variance in the dataset(OR this tells you that 85.4% of the dataset’s variance lies along the first axis), the second accounts for 14.5 percent, and so on. By the fourth feature, less than one-tenth of a percent of the variance is contained in the feature. The other 1,553 features explain even less.

By projecting down to 5D, we lost about 0.05% of the variance:

1-pca.explained_variance_ratio_.sum()

     Here is how to compute the explained variance ratio using the SVD approach (recall that s is the diagonal of the matrix S):

•  s contains all singular values    # U, s, Vt = np.linalg.svd(X_centered)
  OR   & s==>主对角线上的每个元素都称为奇异值的矩阵  via  S[:n,:n]=np.diag(s) and n=X_centered.shape[1]
• np.square(s) ==  eigenvalues;  OR one singular value  特征值eigenvalue取平方根来求奇异值
• The variance explained ratio(方差解释比率或者方差贡献率) of an eigenvalue is simply the fraction of an eigenvalue and the total sum of the eigenvalues:
  

  np.square( pca.singular_values_ ) / np.square( pca.singular_values_ ).sum()

  

  np.diag(pca.singular_values_ )

   

•                           # The amount of variance explained by each of the selected components.
  pca.explained_variance_  # Equal to n_components largest eigenvalues of the covariance matrix of X.

  pca.explained_variance_ #The amount of variance explained by each of the selected components.

  

  total_ev = pca.explained_variance_.sum()
  for ev in pca.explained_variance_:
    print( round( ev/total_ev, 3) )

    == 

     The downside to transforming data with PCA is that these features(Principal components) are often complex combinations of the other features. For example, the first feature(new first axis: first principal component) of the preceding code starts with [-0.092, -0.995, -0.024], that is, multiply the first feature in the original dataset by -0.092, the second by -0.995, the third by -0.024. This feature has 1,558 values of this form, one for each of the original datasets (although many are zeros). Such features are indistinguishable by humans and it is hard to glean [ɡliːn]收集（资料） much relevant information from without a lot of experience working with them.
d: feature columns

############################

from sklearn.preprocessing import StandardScaler

sc = StandardScaler()
X_std = sc.fit_transform(X)

from sklearn.decomposition import PCA

pca_std = PCA( n_components=5 )
Xd_std = pca_std.fit_transform(X_std)

np.set_printoptions( precision=3, suppress=True )
pca_std.explained_variance_ratio_

==>PCA directions are highly sensitive to data scaling

clf = DecisionTreeClassifier( random_state=14 )
scores_reduced_Xd_std = cross_val_score( clf, Xd_std, y, scoring='accuracy',cv=3 )
scores_reduced_Xd_std

############################

from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_val_score

clf = DecisionTreeClassifier( random_state=14 )
scores_reduced_Xd = cross_val_score( clf, Xd, y, scoring='accuracy',cv=3 )
scores_reduced_Xd

 

clf = DecisionTreeClassifier( random_state=14 )
scores_reduced_X = cross_val_score( clf, X, y, scoring='accuracy',cv=3 )
scores_reduced_X

 

scores_reduced_Xd.mean(), scores_reduced_X.mean(), scores_reduced_Xd_std.mean()

 

     The resulting mean score is 0.9385(based on Xd_std), which is (slightly) higher than our original score using all of the original features. PCA won't always give a benefit like this, but it does more often than not.

     We are using PCA here to reduce the number of features in our dataset. As a general rule, you shouldn't use it to reduce overfitting in your data mining experiments. The reason for this is that PCA doesn't take classes into account. A better solution is to use regularization. An introduction, with code, is available at http://blog.datadive.net/selecting-good-features-part-ii-linear-modelsand-regularization/.

     Another advantage is that PCA allows you to plot datasets that you otherwise couldn't easily visualize. For example, we can plot the first two features returned by PCA.

%matplotlib inline
from matplotlib import pyplot as plt

classes = set(y) # converters[1558] = lambda x: 1 if x.strip() == 'ad.' else 0
classes

 

colors = ['red', 'blue']

import seaborn as sns

plt.figure( figsize=(10,8) )
sns.set_style('whitegrid')

for cur_class, color in zip( classes, colors ):
  mask = (y==cur_class).values # type(y) : pandas.core.series.Series
  plt.scatter( Xd[mask, 0], Xd[mask,1], marker='o', color=color, label=int(cur_class) )
plt.legend()
plt.show()

 

Creating your own transformer

     As the complexity and type of dataset changes, you might find that you can't find an existing feature extraction transformer that fits your needs. We will see an example of this in Chapter 7, Discovering Accounts to Follow Using Graph Mining, where we create new features from graphs.

     A transformer is akin类似的 to a converting function. It takes data of one form as input and returns data of another form as output. Transformers can be trained using some training dataset, and these trained parameters can be used to convert testing data.

     The transformer API is quite simple. It takes data of a specific format as input and returns data of another format (either the same as the input or different) as output. Not much else is required of the programmer.

The transformer API

 Transformers have two key functions:

• • fit(): This takes a training set of data as input and sets internal parameters
• • transform(): This performs the transformation itself. This can take either the training dataset, or a new dataset of the same format

     Both fit() and transform() fuction should take the same data type as input, but transform() can return data of a different type. 

     We are going to create a trivial transformer to show the API in action. The transformer will take a NumPy array as input, and discretize it based on the mean. Any value higher than the mean (of the training data) will be given the value 1 and any value lower or equal to the mean will be given the value 0.

     We are going to create a trivial transformer to show the API in action. The transformer will take a NumPy array as input, and discretize it based on the mean. Any value higher than the mean (of the training data) will be given the value 1 and any value lower or equal to the mean will be given the value 0.

Implementation details

     To start, open up the IPython Notebook that we used for the Adult dataset. Then, click on the Cell menu item and choose Run All. This will rerun all of the cells and ensure that the notebook is up to date.

     First, we import the TransformerMixin, which sets the API for us. While Python doesn't have strict interfaces (as opposed to languages like Java), using a mixin like this allows scikit-learn to determine that the class is actually a transformer. We also need to import a function that checks the input is of a valid type. We will use that soon.

class MeanDiscrete( TransformerMixin ):
  def fit(self, X, y=None):
    X = as_float_array(X)
    self.mean = X.mean(axis=0)
    return self

  def transform( self, X, y=None ):
    X = as_float_array(X)
    assert X.shape[1] == self.mean.shape[0]
    # simply testing if the values in X are higher than the stored mean.
    return X> self.mean

mean_discrete = MeanDiscrete()
X_mean = mean_discrete.fit_transform(X)

Unit testing

     When creating your own functions and classes, it is always a good idea to do unit testing. Unit testing aims to test a single unit of your code. In this case, we want to test that our transformer does as it needs to do.

     Good tests should be independently verifiable. A good way to confirm the legitimacy of your tests is by using another computer language or method to perform the calculations. In this case, I used Excel to create a dataset, and then computed the mean for each cell. Those values were then transferred here.

     Unit tests should also be small and quick to run. Therefore, any data used should be of a small size. The dataset I used for creating the tests is stored in the Xt variable from earlier, which we will recreate in our test. The mean of these two features is 13.5 and 15.5, respectively.

Xt

Xt.mean(axis=0)

 

     To create our unit test, we import the assert_array_equal function from NumPy's testing, which checks whether two arrays are equal:

from numpy.testing import assert_array_equal

     Next, we create our function. It is important that the test's name starts with test_, as this nomenclature[nəˈmenklətʃər,ˈnoʊmənkleɪtʃər]命名法  is used for tools that automatically find and run tests. We also set up our testing data:

def test_meandiscrete():
    X_test = np.array([ [ 0,  2],
                        [ 3,  5],
                        [ 6,  8],
                        [ 9, 11],
                        [12, 14],
                        [15, 17],
                        [18, 20],
                        [21, 23],
                        [24, 26],
                        [27, 29]
                      ])
    mean_discrete = MeanDiscrete()
    mean_discrete.fit(X_test)

    assert_array_equal( mean_discrete.mean, np.array([13.5, 15.5]) )
    X_transformed = mean_discrete.transform(X_test)
    X_expected = np.array([ [ 0, 0],
                            [ 0, 0],
                            [ 0, 0],
                            [ 0, 0],
                            [ 0, 0],
                            [ 1, 1],
                            [ 1, 1],
                            [ 1, 1],
                            [ 1, 1],
                            [ 1, 1]
                          ])
    assert_array_equal( X_transformed, X_expected )

test_meandiscrete()

     there was no error, then the test ran without an issue! You can verify this by changing some of the tests to deliberately incorrect values, and seeing that the test fails. Remember to change them back so that the test passes.

##assert_array_equal( mean_discrete.mean, np.array([13,5, 15.5]) )##
test_meandiscrete()

Putting it all together

     Now that we have a tested transformer, it is time to put it into action. Using what we have learned so far, we create a Pipeline, set the first step to the MeanDiscrete transformer, and the second step to a Decision Tree Classifier. We then run a cross validation and print out the result. Let's look at the code: 

from sklearn.pipeline import Pipeline

pipeline = Pipeline([ ('mean_discrete', MeanDiscrete()),
                      ('classifier', DecisionTreeClassifier(random_state=14)),
                    ])
scores_mean_discrete = cross_val_score( pipeline, X,y, scoring='accuracy' )

print('Mean Discrete performance: {0:.3f}'.format( scores_mean_discrete.mean() ) )

 The result is 0.803, which is not as good as before, but not bad for simple binary features.

Summary

     In this chapter, we looked at features and transformers and how they can be used in the data mining pipeline. We discussed what makes a good feature and how to algorithmically choose good features from a standard set. However, creating good features is more art than science and often requires domain knowledge and experience.

     We then created our own transformer using an interface that allows us to use it in scikit-learn's helper functions. We will be creating more transformers in later chapters so that we can perform effective testing using existing functions.

     In the next chapter, we use feature extraction on a corpus of text documents. There are many transformers and feature types for text, each with their advantages and disadvantages.