Datawhale 6月学习——图神经网络:基于GNN的节点表征学习
前情回顾
- 图神经网络:图数据表示及应用
- 图神经网络:消息传递图神经网络
1 图节点表征学习
即学习图中节点上的特征。
在节点预测任务中,我们拥有一个图,图上有很多节点,部分节点的预测标签已知,部分节点的预测标签未知。我们的任务是根据节点的属性(可以是类别型、也可以是数值型)、边的信息、边的属性(如果有的话)、已知的节点预测标签,对未知标签的节点做预测。
这里可以通过一个案例来进行理解(案例及图来自TA补充课:Graph Neural Network (1/2))。
我们要预测一个电视剧里预测谁是凶手
可以把人物作为孤立的一个个案例,来训练分类器进行预测
也可以在一个人物关系图谱下去预测,在这里,人物就是图中的节点,预测人是否为凶手就是一种节点表征学习。
2 节点分类任务——基于Cora数据集
2.1 任务描述
为了展现图神经网络相对常规神经网络的优越性,教程设计了节点分类任务,使用MLP、GCN、GAT三种神经网络进行训练,来比较三者的节点表征能力。
2.1.1 模型简介
上述三种神经网络的简单介绍如下:
- MLP,Multilayer Perceptron,多层感知机,是前馈人工神经网络的一种,为最基础常用的神经网络模型。

- GCN,Graph Convolutional Networks,图卷积神经网络,定义来源于Semi-supervised Classification with Graph Convolutional Network,在hidden layers上实现消息的逐层传播。(图片来源于Graph Convolutional Networks——THOMAS KIPF)
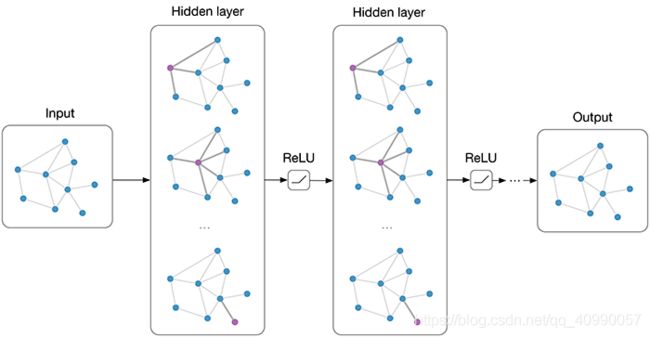
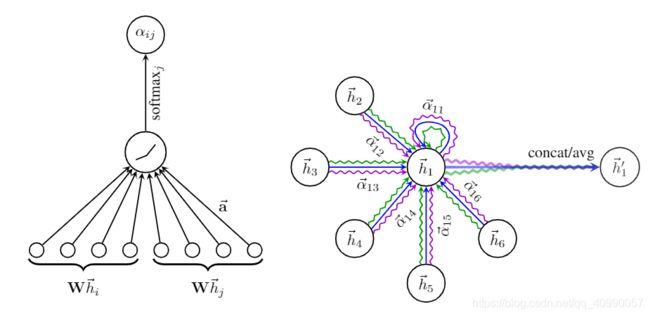
- GAT,Graph Attention Networks,图注意网络,定义来源于论文Graph Attention Networks,引入了attention机制。
2.1.2 数据集描述
在这里使用的是Cora数据集。
Cora是一个论文引用网络,节点代表论文,如果两篇论文存在引用关系,那么认为对应的两个节点之间存在边,每个节点由一个1433维的词包特征向量描述。我们的任务是推断每个文档的类别(共7类)。
from torch_geometric.datasets import Planetoid
from torch_geometric.transforms import NormalizeFeatures
dataset = Planetoid(root='data/Planetoid', name='Cora', transform=NormalizeFeatures())
data = dataset[0] # Get the first graph object.
print()
print(data)
print('======================')
# Gather some statistics about the graph.
print(f'Number of nodes: {data.num_nodes}')
print(f'Number of edges: {data.num_edges}')
print(f'Average node degree: {data.num_edges / data.num_nodes:.2f}')
print(f'Number of training nodes: {data.train_mask.sum()}')
print(f'Training node label rate: {int(data.train_mask.sum()) / data.num_nodes:.2f}')
print(f'Contains isolated nodes: {data.contains_isolated_nodes()}')
print(f'Contains self-loops: {data.contains_self_loops()}')
print(f'Is undirected: {data.is_undirected()}')
输出部分属性,有2708个节点,10556条边,平均节点度为3.90,总共140个节点已有标签,仅占到所有节点数的5%(根据数据集描述,有标签的节点数恰为每类20个)。
进一步地,这个图是无向图,不存在孤立的节点(即每个文档至少有一个引文)。
Data(edge_index=[2, 10556], test_mask=[2708], train_mask=[2708], val_mask=[2708], x=[2708, 1433], y=[2708])
======================
Number of nodes: 2708
Number of edges: 10556
Average node degree: 3.90
Number of training nodes: 140
Training node label rate: 0.05
Contains isolated nodes: False
Contains self-loops: False
Is undirected: True
为了进行训练,首先进行data transformation,此例中,使用的是NormalizeFeatures,进行节点特征归一化,使各节点特征总和为1。
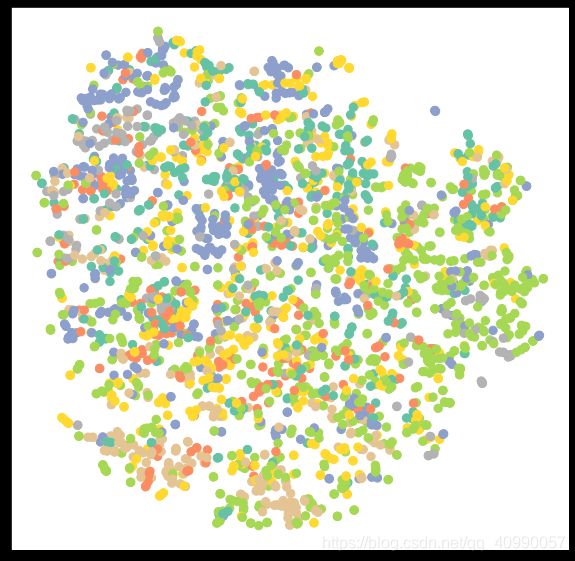
此外,为了实现节点可视化,先定义可视化函数
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
def visualize(h, color):
z = TSNE(n_components=2).fit_transform(out.detach().cpu().numpy())
plt.figure(figsize=(10,10))
plt.xticks([])
plt.yticks([])
plt.scatter(z[:, 0], z[:, 1], s=70, c=color, cmap="Set2")
plt.show()
使用TSNE将高维节点表征嵌入到二维平面空间,然后在二维平面空间画出节点。可视化如下
2.2 模型应用
2.2.1 MLP在图节点分类的应用
在此处,由于MLP不具备分析图结构的能力,故此处应用MLP时将图结构信息忽略,将节点作为独立案例,来进行预测。
理论上,我们应该能够仅根据文件的内容,即它的词包特征表示来推断文件的类别,而无需考虑文件之间的任何关系信息。让我们通过构建一个简单的MLP来验证这一点,该网络只对输入节点的特征进行操作,它在所有节点之间共享权重。
在PyTorch中建立MLP图节点分类器如下
import torch
from torch.nn import Linear
import torch.nn.functional as F
class MLP(torch.nn.Module):
def __init__(self, hidden_channels):
super(MLP, self).__init__()
torch.manual_seed(12345)
self.lin1 = Linear(dataset.num_features, hidden_channels)
self.lin2 = Linear(hidden_channels, dataset.num_classes)
def forward(self, x):
x = self.lin1(x)
x = x.relu()
x = F.dropout(x, p=0.5, training=self.training)
x = self.lin2(x)
return x
建立MLP模型时覆写了torch.nn.Module类,这个类默认执行forward()方法,故主要功能需要在这个方法中实现。
这个MLP模型有一头一尾两个线性变换层,一个使用ReLU作为激活函数的非线性层,和一个dropout来减少过拟合。
此处将预测目标类别空间处理为类别独热编码,预测结果对应概率
我们的MLP由两个线程层、一个
ReLU非线性层和一个dropout操作。第一线程层将1433维的特征向量嵌入(embedding)到低维空间中(hidden_channels=16),第二个线性层将节点表征嵌入到类别空间中(num_classes=7)。
定义cost function为交叉熵损失函数(cross-entropy)
C = − 1 n ∑ x [ y ln ( a ) + ( 1 − y ) ln ( 1 − a ) ] C=-\frac{1}{n}\displaystyle\sum_x[y\ln(a)+(1-y)\ln(1-a)] C=−n1x∑[yln(a)+(1−y)ln(1−a)]
使用Adam优化进行训练
需要先将前面写的MLP类实例化,并进入training mode才可以开始训练。
model = MLP(hidden_channels=16)
criterion = torch.nn.CrossEntropyLoss() # Define loss criterion.
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4) # Define optimizer.
def train():
model.train() #activate training mode
optimizer.zero_grad() # Clear gradients.
out = model(data.x) # Perform a single forward pass.
loss = criterion(out[data.train_mask], data.y[data.train_mask]) # Compute the loss solely based on the training nodes.
loss.backward() # Derive gradients.
optimizer.step() # Update parameters based on gradients.
return loss
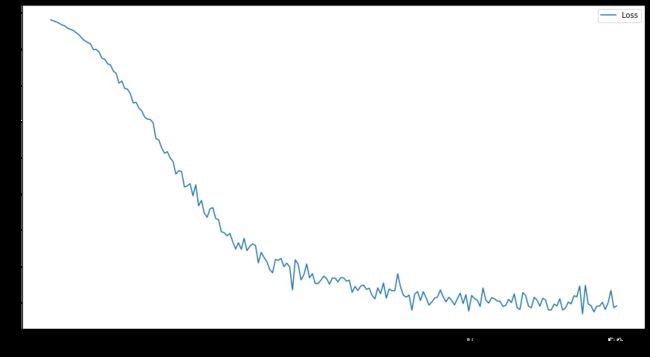
训练并绘制出损失函数图像
import pandas as pd
df = pd.DataFrame(columns = ["Loss"])
df.index.name = "Epoch"
for epoch in range(1, 201):
loss = train()
df.loc[epoch] = loss.item()
df.plot()
def test():
model.eval()
out = model(data.x)
pred = out.argmax(dim=1) # Use the class with highest probability.
test_correct = pred[data.test_mask] == data.y[data.test_mask] # Check against ground-truth labels.
test_acc = int(test_correct.sum()) / int(data.test_mask.sum()) # Derive ratio of correct predictions.
return test_acc
test_acc = test()
print(f'Test Accuracy: {test_acc:.4f}')
在训练集上的准确率为 59.00%,并不高。
2.2.2 GCN在图节点分类的应用
GCN的数学定义为,
X ′ = D ^ − 1 / 2 A ^ D ^ − 1 / 2 X Θ , \mathbf{X}^{\prime} = \mathbf{\hat{D}}^{-1/2} \mathbf{\hat{A}} \mathbf{\hat{D}}^{-1/2} \mathbf{X} \mathbf{\Theta}, X′=D^−1/2A^D^−1/2XΘ,
其中 A ^ = A + I \mathbf{\hat{A}} = \mathbf{A} + \mathbf{I} A^=A+I表示插入自环的邻接矩阵, D ^ i i = ∑ j = 0 A ^ i j \hat{D}_{ii} = \sum_{j=0} \hat{A}_{ij} D^ii=∑j=0A^ij表示其对角线度矩阵。邻接矩阵可以包括不为 1 1 1的值,当邻接矩阵不为{0,1}值时,表示邻接矩阵存储的是边的权重。 D ^ − 1 / 2 A ^ D ^ − 1 / 2 \mathbf{\hat{D}}^{-1/2} \mathbf{\hat{A}} \mathbf{\hat{D}}^{-1/2} D^−1/2A^D^−1/2对称归一化矩阵。
通俗地讲,就是加入自环边(保留自身信息),同时将邻接节点的信息传入本节点,从而实现信息的沿图结构传递。
在PyG中,有内置GCNConv模块,可以调用,详情内容可参阅GCNConv官方文档。
此处通过替换torch.nn.Linear layers为GCNConvlayers,可以实现转化为GNN模型。
from torch_geometric.nn import GCNConv
class GCN(torch.nn.Module):
def __init__(self, hidden_channels):
super(GCN, self).__init__()
torch.manual_seed(12345)
self.conv1 = GCNConv(dataset.num_features, hidden_channels)
self.conv2 = GCNConv(hidden_channels, dataset.num_classes)
def forward(self, x, edge_index):
x = self.conv1(x, edge_index)
x = x.relu()
x = F.dropout(x, p=0.5, training=self.training)
x = self.conv2(x, edge_index)
return x
训练及测试的代码与MLP模型类似,训练过程的损失函数如下,200个epoch后测试集上的准确度为81.4%。
增加epoch数后会出现过拟合,可以进行调参控制早停,有待后续补充。

为了直观的看出训练效果,可以将高维节点表征嵌入到二维平面空间,可视化如下

2.2.3 GAT在图节点分类任务中的应用
图注意网络(GAT)的数学定义为
x i ′ = α i , i Θ x i + ∑ j ∈ N ( i ) α i , j Θ x j , \mathbf{x}^{\prime}_i = \alpha_{i,i}\mathbf{\Theta}\mathbf{x}_{i} + \sum_{j \in \mathcal{N}(i)} \alpha_{i,j}\mathbf{\Theta}\mathbf{x}_{j}, xi′=αi,iΘxi+j∈N(i)∑αi,jΘxj,
其中注意力系数 α i , j \alpha_{i,j} αi,j的计算方法为,
α i , j = exp ( L e a k y R e L U ( a ⊤ [ Θ x i ∥ Θ x j ] ) ) ∑ k ∈ N ( i ) ∪ { i } exp ( L e a k y R e L U ( a ⊤ [ Θ x i ∥ Θ x k ] ) ) . \alpha_{i,j} = \frac{ \exp\left(\mathrm{LeakyReLU}\left(\mathbf{a}^{\top} [\mathbf{\Theta}\mathbf{x}_i \, \Vert \, \mathbf{\Theta}\mathbf{x}_j] \right)\right)} {\sum_{k \in \mathcal{N}(i) \cup \{ i \}} \exp\left(\mathrm{LeakyReLU}\left(\mathbf{a}^{\top} [\mathbf{\Theta}\mathbf{x}_i \, \Vert \, \mathbf{\Theta}\mathbf{x}_k] \right)\right)}. αi,j=∑k∈N(i)∪{i}exp(LeakyReLU(a⊤[Θxi∥Θxk]))exp(LeakyReLU(a⊤[Θxi∥Θxj])).
简单来说,由于引入了注意力机制及softmax,在GAT中,图中的每个节点可以根据邻节点的特征,为其分配不同的权值。
在PyG中已经构建了GATConv构造函数,详情内容可以参阅GATConv官方文档
将MLP例子中的linear层替换为GATConv层,可以实现基于GAT的图节点分类神经网络
import torch
from torch.nn import Linear
import torch.nn.functional as F
from torch_geometric.nn import GATConv
class GAT(torch.nn.Module):
def __init__(self, hidden_channels):
super(GAT, self).__init__()
torch.manual_seed(12345)
self.conv1 = GATConv(dataset.num_features, hidden_channels)
self.conv2 = GATConv(hidden_channels, dataset.num_classes)
def forward(self, x, edge_index):
x = self.conv1(x, edge_index)
x = x.relu()
x = F.dropout(x, p=0.5, training=self.training)
x = self.conv2(x, edge_index)
return x
训练及测试的代码与MLP模型类似,训练过程的损失函数如下,200个epoch后测试集上的准确度为73.8%,且从损失函数图像上看训练已基本完成,但这一准确性结果与论文Pitfalls of Graph Neural Network Evaluation所提供的结果81.8+1.3%相去甚远,需要通过验证集进行调参,已达到更好的效果,有待后续补充。
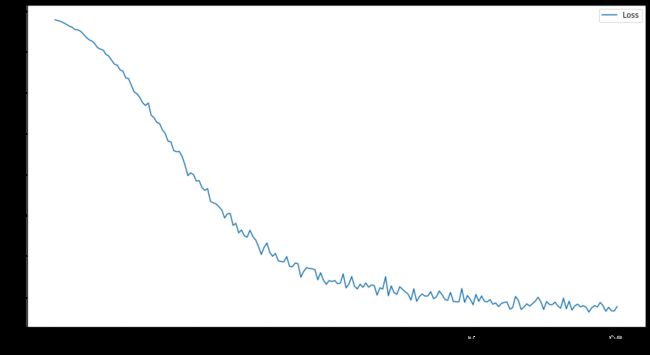
为了直观的看出训练效果,可以将高维节点表征嵌入到二维平面空间,可视化如下

2.3 对比分析
显然MLP在处理这一问题的时候,由于未考虑节点间的相互关系,其训练效果很差,而考虑了节点属性及邻居节点属性的GCN和GAT模型训练效果较好。但并非是在所有的问题中,这一表现都明显。
GCN及GAT模型在考虑邻居节点属性的传入的过程,都遵循上一个task学到的消息传递范式,而教程中也提供了GCN及GAT的消息聚合方法的对比:
GCN与GAT的区别在于邻居节点信息聚合过程中的归一化方法不同:
- 前者根据中心节点与邻居节点的度计算归一化系数,后者根据中心节点与邻居节点的相似度计算归一化系数。
- 前者的归一化方式依赖于图的拓扑结构,不同节点其自身的度不同、其邻居的度也不同,在一些应用中可能会影响泛化能力。
- 后者的归一化方式依赖于中心节点与邻居节点的相似度,相似度是训练得到的,因此不受图的拓扑结构的影响,在不同的任务中都会有较好的泛化表现。
3 节点分类任务——基于CiteSeer数据集(作业)
3.1 数据集
选用Planetoid的CiteSeer数据集进行此项任务,CiteSeer数据集和Cora一样,是采用了训练集每类20个的数据集划分方式,其基本信息如下
Number of features: 3703
Number of classes: 6
Number of nodes: 3327
Number of edges: 9104
Average node degree: 2.74
Number of training nodes: 120
Training node label rate: 0.04
Contains isolated nodes: True
Contains self-loops: False
Is undirected: True
3.2 训练
3.2.1 MLP
依然使用有两个线性层一个ReLU层及一个dropout的MLP网络进行训练,参数设置参见2.2.1,结果准确率为58.20%。
3.2.2 GCN
依然使用有两个GCNConv层一个ReLU层及一个dropout的GCN网络进行训练,参数设置参见2.2.2,结果准确率为71.2%,需要早停,节点可视化如下
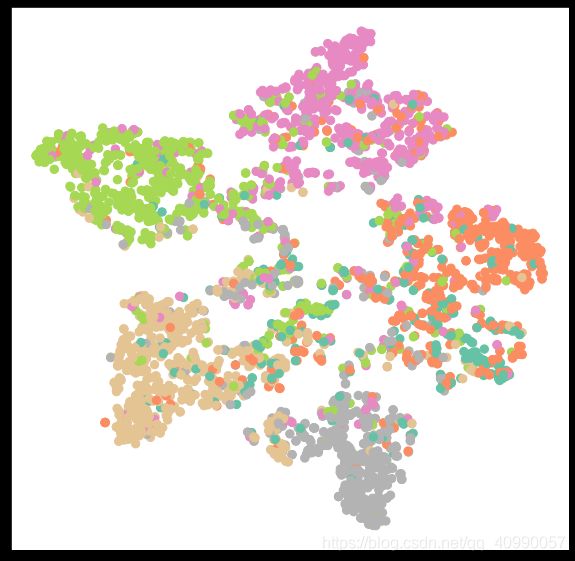
3.2.3 GAT
依然使用有两个GATConv层一个ReLU层及一个dropout的GAT网络进行训练,参数设置参见2.2.3,结果准确率为61.0%,节点可视化如下

3.2.4 GraphSAGE
GraphSAGE(Graph SAmple and aggreGatE)是一种归纳学习框架,来源于论文Inductive Representation Learning on Large Graphs。
![]()
这是一种归纳学习方法,通过训练聚合节点邻居的函数(卷积层),使GCN扩展成归纳学习任务,对未知节点起到泛化作用。
公式如下
x i ′ = W 1 x i + W 2 m e a n ( x j ) x_i'=W_1x_i+W_2 mean(x_j) xi′=W1xi+W2mean(xj)
在PyG中有现成的模块SAGEConv可以调用。构建GraphSAGE网络如下。
from torch_geometric.nn import SAGEConv
class SAGE(torch.nn.Module):
def __init__(self, hidden_channels):
super(GAT, self).__init__()
torch.manual_seed(12345)
self.conv1 = SAGEConv(dataset.num_features, hidden_channels)
self.conv2 = SAGEConv(hidden_channels, dataset.num_classes)
def forward(self, x, edge_index):
x = self.conv1(x, edge_index)
x = x.relu()
x = F.dropout(x, p=0.5, training=self.training)
x = self.conv2(x, edge_index)
return x
epoch数设置为200,训练损失函数如下
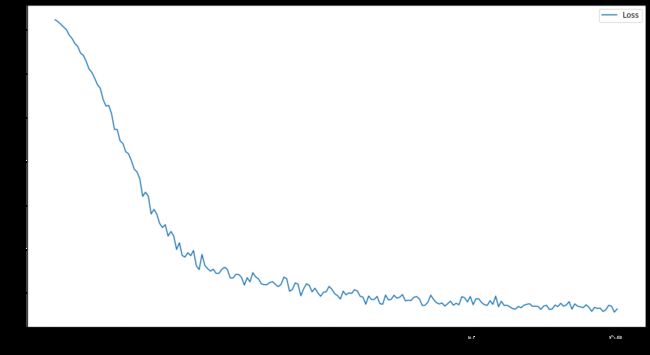
结果准确率为69.8%,节点可视化如下

3.3 分类模型对比
此处借鉴了论文Pitfalls of Graph Neural Network Evaluation 中提供的结果
该论文比较了常见模型在典型GNN可用数据集上的效果
结果如下

可以看到,并非所有的数据集在加入图结构(节点沿边信息传递)后,准确率都有大幅度的提升。
而且训练集及测试集的划分,也有一定的影响。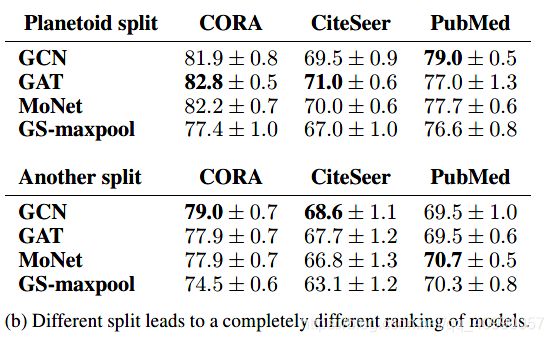
参考阅读
- Datawhale组队学习
- Multilayer perceptron
- Graph Attention Networks阅读笔记
- GraphSAGE: GCN落地必读论文