MATLAB实现智能计算方法实验：实验四 RBF神经网络

资源链接

MATLAB实现智能计算方法课程所有实验代码资源链接为：MATLAB实现智能计算方法课程所有实验代码资源

实验汇总

MATLAB实现智能计算方法课程所有实验汇总博客链接为：MATLAB实现智能计算方法实验汇总

实验目的

1. 通过本次实验，进一步理解多层感知器、RBF网络的模型结构与计算原理；
2. 掌握手工计算过程和编码，并能够解决实际问题；
3. 掌握MATLAB工具箱中的RBF相关函数，用工具箱实现编程，解决实际问题。

实验内容

1. 利用RBF神经网络，解决异或问题

1. 异或问题本质上是一个二分类问题：输入为向量[x1,x2]，输出是标量，取值限定为0或1。

   序号	x1	x2	D期望输出
   1	0	0	0
   2	0	1	1
   3	1	0	1
   4	1	1	0

2. 设计网络结构（以图的形式放入报告）；

3. 手工编码（python或MATLAB），实现对异或问题的分类计算。

4. 用MATLAB工具箱编程实现模型仿真。

   测试数据1:x1=0.95，x2=0.03。
   测试数据2:x1=0.92,x2=0.89。

2. 曲线拟合

1. 给定一系列已知的采样点，就可以近似确定在某未知自变量位置处的函数值(18个点)

   X=-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,8,9
   Y=-129,-32,-118,-138,-125,-97,-55,-23,-4,2,1,-31,-72,-121,-142,-174,-155,-77

2. 手工编码（python或MATLAB），实现曲线拟合。

3. 用MATLAB工具箱编程实现曲线拟合，改变spread，观察拟合结果并截图放入报告中。

实验步骤

1. 设计网络结构

设计具有一层隐含层，隐含层为4个神经单元，输入层有2个神经单元，输出层有1个神经单元的RBF神经网络，网络结构如下图1。

图1 RBF网络结构

2. 利用RBF神经网络，解决异或问题

1. 手工编码

clc;
clear;
P = [0, 0, 1, 1; 0, 1, 0, 1];
T = [0, 1, 1, 0];
t = [0 1; 0 1];
z = dist(P', t);
G = radbas(z);
G  =[G, ones(4,1)];
%G.'*G的逆矩阵*G.'
w = G'*G\G'*T';
Y = G*w;
disp('训练输出');
disp(Y');
P1 = [0.95 0.92; 0.03 0.89];
z1 = dist(P1', t);
G1 = radbas(z1);
G1 = [G1, ones(2,1)];
T1 = G1*w;
disp('测试输出');
disp(T1');

执行程序，输出结果如下图2。

图2 手工编码分类结果

2. 工具箱仿真

应用MATLAB工具箱编程实现模型仿真并用测试数据进行预测，程序代码如下：

clc
clear
P = [0, 0, 1, 1; 0, 1, 0, 1];
T = [0, 1, 1, 0];
%创建正规化网络
net = newrbe(P, T);
out = sim(net, P);
disp('训练输出');
disp(out);
P1 = [0.95 0.92; 0.03 0.89];
out1 = sim(net, P1);
disp('测试输出')
disp(out1);

执行程序，输出结果如下图3。

图3 工具箱分类结果

3. 曲线拟合

1. 手工编码

clc;
clear;
M = 10;
centers = [];
deltas = [];
set = {};
gap = 0.01;
X = -9: 1: 8; 
P = length(X);
Y = [-129 -32 -118 -138 -125 -97 -55 -23 -4 2 1 -31 -72 -121 -142 -174 -155 -77];
A = randperm(M);
for i = 1: M 
    centers(i) = X(A(i));
end 
done = 0; 
while(~done) 
    for i = 1: M 
       set{i} = [];
    end 
    for i = 1: P 
        distance = 100;
        for j = 1: M 
            curr = abs(X(i) - centers(j)); 
            if curr < distance 
                sets = j;
                distance = curr;
            end 
        end 
        set{sets} = [set{sets}, X(i)];  
    end
    for i = 1: M 
        new_centers(i) = sum(set{i})/length(set{i}); 
        sum1(i) = abs(centers(i) - new_centers(i));
    end 
    if sum(sum1) > gap 
        done = 0;      
        centers = new_centers; 
    else 
        done = 1; 
    end    
end

for i = 1: M
    curr = abs(centers - centers(i)); 
    [curr_2, b] = min(curr); 
    curr(b) = 100; 
    curr_2 = min(curr); 
    deltas(i) = 2*curr_2; 
end
for i = 1: P 
    for j = 1: M 
        curr = abs(X(i) - centers(j)); 
        K(i, j) = exp(-curr^2/(2*deltas(j)^2) );  
    end 
end 
weights = K'*K\K'*Y'; 
X1 = -9: .1: 8;   
for i = 1: length(X1) 
    sum = 0; 
    for j = 1:M 
        curr = weights(j)*exp(-abs(X1(i) - centers(j))^2/(2*deltas(j)^2)); 
        sum = sum + curr; 
    end 
    Y1(i)=sum; 
end 
figure;
scatter(X, Y, 'o'); 
hold on; 
plot(X1, Y1, 'b-')

拟合结果如下。

图4 手工编码拟合结果

2. 工具箱仿真

应用MATLAB工具箱编程实现模型仿真并用测试数据进行预测，程序代码如下，并设置不同spread，得到不同的拟合结果。

clc;
clear;
P = -9: 1: 8;
T = [-129,-32,-118,-138,-125,-97,-55,-23,-4,2,1,-31,-72,-121,-142,-174,-155,-77];
spread = 0.5;
tic;
net = newrbe(P, T, spread);
test = -9: .1: 8;
out = sim(net, test);
toc;
figure;
plot(P, T, 'o')
hold on;
plot(test, out, 'b-');
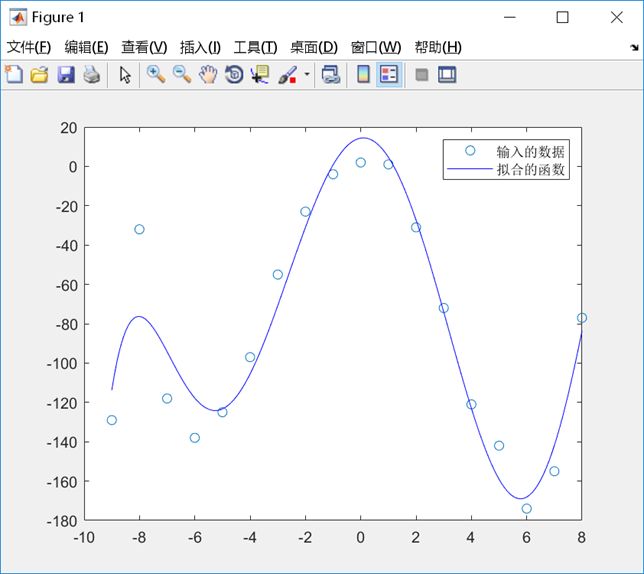
legend('输入的数据', '拟合的函数');

• Spread为200

图5 工具箱Spread为200

• Spread为1

图6 工具箱Spread为1

• Spread为0.5

图7 工具箱Spread为0.5

观察不同spread运行的结果，可以发现，spread越大，拟合的函数越平滑，但效果也越差，反之，spread越小，平滑度越差，但离群点会变少，然而spread太小，拟合的函数效果也会变差。综合上述三幅图，发现spread为1时效果最好。