动手学深度学习--pytorch--线性回归,softmax--(2)
线性回归
用一个线性回归来预测房价 首先明确问题
我们以一个简单的房屋价格预测作为例子来解释线性回归的基本要素。这个应用的目标是预测一栋
房子的售出价格(元)。我们知道这个价格取决于很多因素,如房屋状况、地段、市场行情等。为了简
单起见,这里我们假设价格只取决于房屋状况的两个因素,即面积(平方米)和房龄(年)。接下来我
们希望探索价格与这两个因素的具体关系。
设房屋的面积为 ,房龄为 ,售出价格为 。我们需要建立基于输入 和 来计算输出 的表达
式,也就是模型(model)。顾名思义,线性回归假设输出与各个输入之间是线性关系:
![]()
其中w1和w2是权重 b是偏差 其实这个线性 回归就是通过梯度下降的方式 去调整这三个参数的值
目的是能适配训练集中的 x和y值 并且把确定好的参数 用于 输入x预测y
我们通常收集一系列的真实数据,例如多栋房屋的真实售出价格和它们对应的面积和房龄。我们希
望在这个数据上面寻找模型参数来使模型的预测价格与真实价格的误差最小。在机器学习术语里,该数
据集被称为训练数据集(training data set)或训练集(training set),一栋房屋被称为一个样本
(sample),其真实售出价格叫作标签(label),用来预测标签的两个因素叫作特征(feature)。特
征用来表征样本的特点。
在模型训练中,我们需要衡量价格预测值与真实值之间的误差。通常我们会选取一个非负数作为误
差,且数值越小表示误差越小。一个常用的选择是平方函数。它在评估索引为 的样本误差的表达式为:

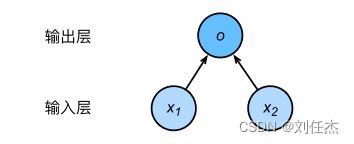
把我们的问题转化成神经网络图可以得到下图
`import matplotlib.pyplot as plt
import random
#sheng cheng shujuji
import torch
import numpy as np
num_inputs = 2
num_examples = 1000
true_w = [2,-3.4]
true_b = 4.2
features = torch.randn(num_examples,num_inputs,dtype = torch.float32)
labels = true_w[0]*features[:,0]+true_w[1]*features[:,1]+true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float32)
#ru xia shi yi ge an pi liang qu shu ju de han shu
def data_iter(batch_size,features,labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices)
for i in range(0,num_examples,batch_size):
j = torch.LongTensor(indices[i:min(i+batch_size,num_examples)])
yield features.index_select(0,j),labels.index_select(0,j)
#ru xia shi chushi hua w b bing qie shenqing ti du
w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32)
b = torch.zeros(1, dtype=torch.float32)
w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)
def linreg(X, w, b):
return torch.mm(X, w) + b
def squared_loss(y_hat, y):
return (y_hat - y.view(y_hat.size())) ** 2 / 2
def sgd(params,lr,batch_size):
for param in params:
param.data -= lr*param.grad/batch_size
lr = 0.03
num_epochs = 5
net = linreg
loss = squared_loss
batch_size = 32
for epoch in range(num_epochs):
for X,y in data_iter(batch_size,features,labels):
l = loss(net(X,w,b),y).sum()
l.backward()
sgd([w,b],lr,batch_size)
w.grad.data.zero_()
b.grad.data.zero_()
train_l = loss(net(features,w,b),labels)
print(‘epoch %d, loss %f’ % (epoch+1, train_l.mean().item()))
`
