机器学习笔记——Kmeans聚类
算法介绍
K-means聚类算是机器学习无监督学习的经典算法了,最早接触的时候是在数模比赛中,那个时候还只停留在使用API上,对K-means算法的核心步骤没有完全搞懂,本文打算详细介绍K-means聚类算法,并给出选择k值的两个方法:手肘法和轮廓系数法,以及所有的code。
K-means原理
原理非常简单,在了解Kmeans算法之前,得知道什么是无监督学习,在机器学习中,无监督学习和有监督学习是两个领域,它们最大得差别就是无监督学习没有标签y,也就是说无监督学习的数据集只包含X,也就是特征数据集,而无监督学习的目的就是找到没有标签y的情况下数据的分布规律以及实用价值。而无监督学习除了聚类还有很多,例如降维、异常值检测,密度估计等。
对于给定的样本集 D = x 1 , x 2 , ⋯ , x m D = {x_1,x_2,\cdots,x_m} D=x1,x2,⋯,xm,K-means算法(又叫K均值算法)的目的在于找到簇划分 C = C 1 , C 2 , ⋯ , C k C={C_1,C_2,\cdots,C_k} C=C1,C2,⋯,Ck,使得误差函数 E E E最小。
E = ∑ i = 1 k ∑ x ∈ C i ∣ ∣ x − μ i ∣ ∣ 2 2 E = \sum\limits_{i=1}^k\sum\limits_{x\in C_i}{||x-\mu_i||_2^2} E=i=1∑kx∈Ci∑∣∣x−μi∣∣22
其中 μ i = 1 ∣ C i ∣ ∑ x ∈ C i x \mu_i=\frac{1}{|C_i|}\sum\limits_{x\in C_i}{x} μi=∣Ci∣1x∈Ci∑x是簇 C i C_i Ci的均值向量,而误差函数 E E E从直观上反映出簇内样本围绕均值向量的紧密程度,如果 E E E值越小,说明簇间的紧密程度越大。
既然找到了学习的目标,我们就想着如何求解上面的模型了。但是求解这个模型并不简单,在所有样本点中找到最合适的簇,这是一个NP难问题,求解非常麻烦,于是我们可以采用一种近似的方法求解,即贪心策略,也就是我们今天要学习的K-means最重要的部分。
下面是K-means算法的步骤
输入:样本集 D = { x 1 , x 2 , ⋯ , x m } D=\{x_1,x_2,\cdots,x_m\} D={x1,x2,⋯,xm} 聚类簇数
- 从样本集 D D D中随机选择 k k k个样本作为初始均值向量 { μ 1 , μ 2 , ⋯ , μ i } \{\mu_1,\mu_2,\cdots,\mu_i\} {μ1,μ2,⋯,μi}
- 遍历所有样本点,计算 x j x_j xj到各个均值向量 μ i \mu_i μi之间的距离 d j i d_{ji} dji,选择 d j i d_{ji} dji最小的均值向量的簇标记 k k k,然后将样本 x j x_j xj划入相应的簇中。
- 更新均值向量。
- 如果当前所有的均值向量的值未改变,则结束算法。
输出:簇划分 C = { C 1 , C 2 , ⋯ C k } C = \{C_1,C_2,\cdots C_k\} C={C1,C2,⋯Ck}
看起来是不是很简单的一个算法,要注意其中的 d i j d_{ij} dij是通过定义的距离函数计算得到的,如果我们选择不同的距离函数,那么我们得到的 d i j d_{ij} dij也是不一样的。
常见的距离函数有欧式距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离等等,另外值得注意的是,这里的距离函数只用于解决连续性属性,在面对类别属性时,我们一般采用其它距离函数。
常见的连续性属性的距离函数定义如下:
欧式距离: d = ∣ ∣ x i − x j ∣ ∣ 2 = ∑ u = 1 n ∣ x i u − x j u ∣ 2 d= ||x_i-x_j||_2=\sqrt {\sum\limits_{u=1}^n{|x_{iu}-x_{ju}|^2}} d=∣∣xi−xj∣∣2=u=1∑n∣xiu−xju∣2 曼哈顿距离: d = ∣ ∣ x i − x j ∣ ∣ 1 = ∑ u = 1 n ∣ x i u − x j u ∣ d= ||x_i-x_j||_1=\sum\limits_{u=1}^n{|x_{iu}-x_{ju}|} d=∣∣xi−xj∣∣1=u=1∑n∣xiu−xju∣
离散属性的定义如下:
令 m u , a m_{u,a} mu,a表示在属性 u u u上取值为 a a a的样本数, m u , a , i m_{u,a,i} mu,a,i表示在第 i i i个样本簇中在属性 u u u上取值为 a a a的样本数, k k k为样本簇数,则属性 u u u上两个离散值 a a a和 b b b之间的
VDM距离为: V D M p ( a , b ) = ∑ i = 1 k ∣ m u , a , i m u , a − m u , b , i m u , b ∣ p VDM_p(a,b) = \sum\limits_{i=1}^k{|\frac{m_{u,a,i}}{m_{u,a}}-\frac{m_{u,b,i}}{m_{u,b}}|^p} VDMp(a,b)=i=1∑k∣mu,amu,a,i−mu,bmu,b,i∣p
于是得到了K-means算法在处理离散属性时所采用的距离公式。 于是可以将处理离散属性和处理连续属性的距离函数结合起来,构成如下的形式:
D ( x i , x j ) = ( ∑ u = 1 n c ∣ x i u − x j u ∣ p + ∑ u = n c + 1 n V D M p ( x i u , x j u ) ) 1 p D(x_i,x_j)=(\sum\limits_{u=1}^{n_c}|x_{iu}-x_{ju}|^p+\sum\limits_{u=n_c+1}^n{VDM_p(x_{iu},x_{ju})})^\frac{1}{p} D(xi,xj)=(u=1∑nc∣xiu−xju∣p+u=nc+1∑nVDMp(xiu,xju))p1
上述 n c n_c nc和 n − n c n-n_c n−nc分别表示离散属性和连续属性的个数。
此外还需要强调的是,K-means计算样本距离的数据必须是经过归一化之后的数据,因为不同量纲下的数据其大小不在一个维度,所以必须去除量纲对训练的影响。
在实战前,还有一个很重要的点没有介绍,那就是K值的选取,作为K-means算法最重要也是唯一的参数,K值的选取直接影响着K-means聚类结果的好坏,在选择最优K值时,一般有两种方法:手肘法和轮廓系数法。
手肘法选择K值
手肘法的思想非常简单,就是通过判断不同的K值其聚类效果的好坏,从而选择最优的K值,评判聚类好坏的标准我们前面已经介绍过了,那就是E,对于不同的K值,我们采用贪心算法求解得到聚类结果,然后计算当前聚类结果的误差大小,绘制误差随着K值的变化图,其实我们可以猜到,随着K值的增大,E的值应该是越来越小的,因为更多的聚类簇数可以让数据更加分散,这样可以减小E的值。例如我们 实例中得到的手肘图如下:
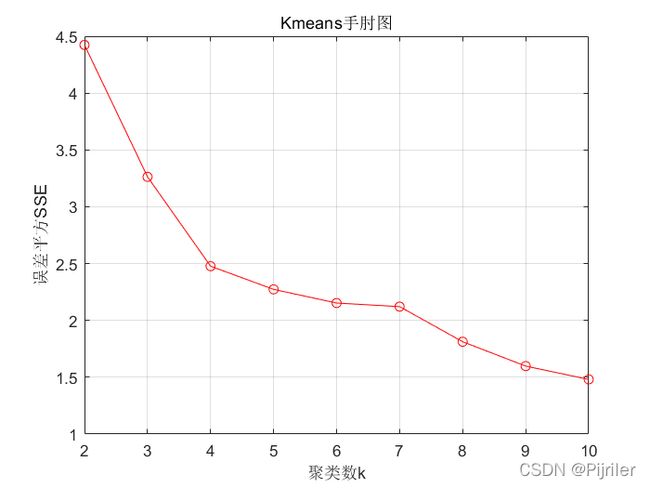
从手肘图上可以明显看出,当误差SSE在聚类数K等于4时存在一个小小的突变,在4之前,误差的下降速度非常快,在4之后,误差下降的速度比较慢,从而构成“手肘状”,这个聚类数4就是我们要找到最优聚类数K。
其实要想理解其原理很简单,随着聚类数K值的增大,样本划分会更加精细,每个簇的聚合程度会逐渐提高,那么误差E自然会变小,并且,当K值小于真实的聚类数时,再增加K所得到的聚合程度回报效果会迅速减小,所以误差的下降幅度就会减小,这就是手肘法的思想。
轮廓系数法
轮廓系数法相较于手肘法来说,我觉得其更据理论性。具体如下:
在手肘法中,我们想找到最优的K值,无非是找到一个合适的评价指标,从评价指标的值来决定最优的K值,而轮廓系数就是轮廓系数所用到的评价指标。轮廓系数的定义如下:
s ( i ) = b ( i ) − a ( i ) m a x { a ( i ) , b ( i ) } s(i)=\frac{b(i)-a(i)}{max\{a(i),b(i)\}} s(i)=max{a(i),b(i)}b(i)−a(i)
上式中, a ( i ) a(i) a(i)为样本到同簇其它样本点的平均距离, a ( i ) a(i) a(i)越小,说明样本 i i i越应该被聚类到此簇,因而也将 a ( i ) a(i) a(i)的值称为样本 i i i的簇内不相似度。 b ( i ) b(i) b(i)是样本 i i i到其它所有簇样本的平均距离最大值,也就是说为了计算 b ( i ) b(i) b(i),得先要计算样本 i i i到其它簇 j j j的平均距离 b i j b_{ij} bij,然后 b ( i ) = m i n { b i 1 , b i 2 , ⋯ , b i k } b(i)=min\{b_{i1},b_{i2},\cdots,b_{ik}\} b(i)=min{bi1,bi2,⋯,bik}, b ( i ) b(i) b(i)反映的是样本 i i i的簇间不相似度,而我们的目的就是找到使得 b ( i ) b(i) b(i)大,使得 a ( i ) a(i) a(i)小的最优聚类数K,于是把 b ( i ) b(i) b(i)和 a ( i ) a(i) a(i)结合得到 s ( i ) s(i) s(i),分母的 m a x { a ( i ) , b ( i ) } max\{a(i),b(i)\} max{a(i),b(i)}应该是将 s ( i ) s(i) s(i)标准化。我理解的是,不同的K值,其 a ( i ) a(i) a(i)和 b ( i ) b(i) b(i)的变化非常大,这样不容易比较,而除以 a ( i ) a(i) a(i)和 b ( i ) b(i) b(i)的最大值,方便比较不同K值情况下的优劣程度,我们将所有样本的 s ( i ) s(i) s(i)求平均值称为轮廓系数。而且可以看出,轮廓系数的取值范围应该是[-1,1],轮廓系数越大,K值越优,绘制轮廓系数随聚类数K值的变化图如下:
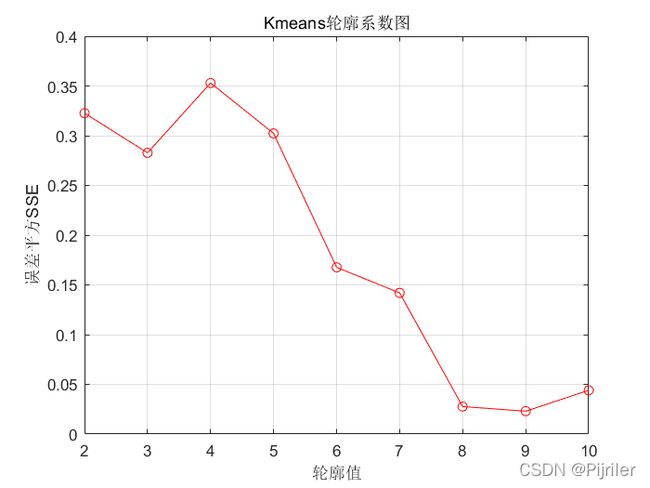
很明显,最优的K值为4,上述的手肘图和轮廓系数图都是一个问题绘制的结果图,两种方法都能看出,当K值等于4时整体的聚类效果最优。
实战
实战部分,我用的是西瓜书上的数据集,因为是二维的好画图,所以作为实战比较好。代码如下:
K-means函数代码
function [results,Mean_vector] = Kmeans(D,k)
%{
solve 进行K均值聚类
Input D——样本训练集
k——聚类的k值
Output results——聚类的结果
Mean_vector——均值向量
%}
% 判断参数的输入是否正确
if nargin < 2
error(message('stats:kmeans:TooFewInputs'));
end
% 获取样本总数量和样本维数
[Sample_number,~] = size(D);
% 随机选择k个样本作为初始均值向量
Random = randperm(Sample_number);
Randindex = Random(1:k);
Mean_vector = D(Randindex,:);
% 定义初始的样本分类存储
D_index = zeros(Sample_number,1);
% 算法进入循环
Until_flag = 0;
while(Until_flag ~= k)
Distance = zeros(Sample_number,k);
% 更新样本归类
for i =1:Sample_number
% 计算样本i与各均值向量的的距离
for j =1:k
Distance(i,j) = norm(D(i,:)-Mean_vector(j,:));
end
% 记录第i个样本的均值归类
[~,min_index] = min(Distance(i,:));
D_index(i) = min_index;
end
% 更新均值向量
Mean_vector_new = zeros(size(Mean_vector));
Until_flag = 0;
for i = 1:k
% 获得第i各均值类别中的样本下标a
[a,~] = find(D_index == i);
Mean_vector_new(i,:) = mean(D(a,:));
if norm(Mean_vector_new(i,:)) == norm(Mean_vector(i,:)) % 如果均值向量未发生变化
Mean_vector(i,:) = Mean_vector(i,:);
Until_flag = Until_flag + 1;
else
Mean_vector(i,:) = Mean_vector_new(i,:);
end
end
end
% 输出结果
results = D_index;
end
手肘法代码
function Kmeans_Elbow(D,n)
%{
solve Kmeans手肘法选择最优K值
Input D——训练数据集
n——最大迭代的k值,默认是10
Output 绘制结果图
%}
% 当只输入一个变量时,此时的最大迭代k值默认为10
if (nargin<2)
n = 10;
end
% 算法主体
Elbow = zeros(n-1,1);
% 遍历所有的k值
for k = 2:n
% 获取样本总数量
[Sample_number,~] = size(D);
% 随机选择k个样本作为初始均值向量
Random = randperm(Sample_number);
Randindex = Random(1:k);
Mean_vector = D(Randindex,:);
% 定义初始的样本分类存储
D_index = zeros(Sample_number,1);
% 定义循环结束标志
Until_flag = 0;
while(Until_flag ~= k)
Distance = zeros(Sample_number,k);
% 更新样本归类
for i =1:Sample_number
% 计算样本i与各均值向量的的距离
for j =1:k
Distance(i,j) = norm(D(i,:) - Mean_vector(j,:));
end
% 记录第i个样本的均值归类
[~,min_index] = min(Distance(i,:));
D_index(i) = min_index;
end
% 更新均值向量
Mean_vector_new = zeros(size(Mean_vector));
Until_flag = 0;
for i = 1:k
% 获得第i各均值类别中的样本下标a
[a,~] = find(D_index == i);
% 当类别中只有一个样本时,则此样本为中心向量
if length(a) == 1
Mean_vector_new(i,:) = D(a,:);
else
Mean_vector_new(i,:) = mean(D(a,:));
end
if norm(Mean_vector_new(i,:)) == norm(Mean_vector(i,:)) % 如果均值向量未发生变化
Mean_vector(i,:) = Mean_vector(i,:);
Until_flag = Until_flag + 1;
elseif (norm(Mean_vector_new(i,:)) ~= norm(Mean_vector(i,:)))&&(sum(isnan(Mean_vector_new(i,:))) == 0)
Mean_vector(i,:) = Mean_vector_new(i,:);
end
end
end
% 计算手肘值
for i =1:k % 遍历所有种类
[a,~] = find(D_index == i);
% 遍历第i个分类的所有样本,累加手肘值
for q = 1:length(a)
Elbow(k-1) = Elbow(k-1) + norm(D(a(q),:) - Mean_vector(i,:));
end
end
end
% 对手肘数据进行可视化
plot(2:n,Elbow,'ro-')
grid on
ylabel('误差平方SSE')
xlabel('聚类数k')
title('Kmeans手肘图')
end
轮廓系数法代码
function Kmeans_Silhouette_Coefficient(D,n)
%{
solve Kmeans轮廓系数法找k值
Input D——训练数据集
n——最大迭代的k值,默认是10
Output 绘制结果图
原理:轮廓系数最大时对应的k值就是最优k值,说明簇内距离小,簇外距离大
%}
% 当只输入一个变量时,此时的最大迭代k值默认为10
if (nargin<2)
n = 10;
end
% 算法主体
Coefficient = zeros(n-1,1);
% 遍历所有的k值
for k = 2:n
% 获取样本总数量
[Sample_number,~] = size(D);
% 随机选择k个样本作为初始均值向量
Random = randperm(Sample_number);
Randindex = Random(1:k);
Mean_vector = D(Randindex,:);
% 定义初始的样本分类存储
D_index = zeros(Sample_number,1);
% 定义循环结束标志
Until_flag = 0;
while(Until_flag ~= k)
Distance = zeros(Sample_number,k);
% 更新样本归类
for i =1:Sample_number
% 计算样本i与各均值向量的的距离
for j =1:k
Distance(i,j) = norm(D(i,:) - Mean_vector(j,:));
end
% 记录第i个样本的均值归类
[~,min_index] = min(Distance(i,:));
D_index(i) = min_index;
end
% 更新均值向量
Mean_vector_new = zeros(size(Mean_vector));
Until_flag = 0;
for i = 1:k
% 获得第i各均值类别中的样本下标a
[a,~] = find(D_index == i);
% 当类别中只有一个样本时,则此样本为中心向量
if length(a) == 1
Mean_vector_new(i,:) = D(a,:);
else
Mean_vector_new(i,:) = mean(D(a,:));
end
if norm(Mean_vector_new(i,:)) == norm(Mean_vector(i,:)) % 如果均值向量未发生变化
Mean_vector(i,:) = Mean_vector(i,:);
Until_flag = Until_flag + 1;
elseif (norm(Mean_vector_new(i,:)) ~= norm(Mean_vector(i,:)))&&(sum(isnan(Mean_vector_new(i,:))) == 0)
Mean_vector(i,:) = Mean_vector_new(i,:);
end
end
end
% 计算轮廓系数
% 定义中间变量
a = zeros(Sample_number,1);
b = zeros(Sample_number,1);
s = zeros(Sample_number,1);
for i =1:Sample_number
% 计算样本到同簇的平均距离a
Temp_index = find((D_index==D_index(i)));
% a_ave_i = zeros(length(Temp_index) - 1,1);
for j = 1:length(Temp_index)
if i~=Temp_index(j)
a_ave_i(j) = norm(D(i,:) - D(Temp_index(j),:));
end
end
a(i) = mean(a_ave_i);
% 计算样本到其它簇的所有样本的平均距离
b_temp = zeros(k,1);
for j = 1:k
if D_index(i) ~= j
Temp_index = find(D_index == j);
b_ave_i = zeros(length(Temp_index),1);
for m = 1:length(Temp_index)
b_ave_i(m) = norm(D(i,:) - D(Temp_index(m),:));
end
b_temp(j) = mean(b_ave_i);
end
end
b_temp(b_temp == 0) = [];
b(i) = min(b_temp);
s(i) = (b(i)-a(i))/(max(a(i),b(i)));
end
% 计算轮廓系数
Coefficient(k-1) = mean(s);
end
% 对手肘数据进行可视化
plot(2:n,Coefficient,'ro-')
grid on
ylabel('误差平方SSE')
xlabel('轮廓值')
title('Kmeans轮廓系数图')
end
总结
其实本文的K-means算法大致内容已经介绍完毕。还有的一些就是对Kmeans++的改进,既然有改进,那就必须找到现有K-means算法的不足之处。K-means算法的改进版本还是很多的,有K-means++、MinibatchK-means、加速K-means等等,其中我习惯用的就是K-means++,该改进算法与其它改进算法的侧重点有不同点,常规K-means算法在选择初始簇心时的不足,改进常规的随机选择,使用一种启发式方法来选择簇心,这个启发式方法就是轮盘赌法。剩下的就不一一介绍了。
至于K-means算法的应用方面,我觉得最大的用处还是对原始数据进行聚类,虽然可以用到数据预处理和半监督学习上去,但是效果其实并不是很好(个人看法)。