NNDL 作业7：第五章课后题（1×1 卷积核 | CNN BP）

---

习题

5-2证明宽卷积具有交换性。即公式$rot180(W)⨂X=rot180(X)⨂W$

  如果不限制两个卷积信号的长度，真正的翻转卷积是具有交换性的，即$x\ast y=y\ast x.$对于互相关的的“卷积”，也具有一定的“交换性”。
  我们先介绍宽卷积（Wide Convolution）的定义。给定一个二维图像$X\in {\mathbb{R}}^{M\times N}$和一个二维卷积核$W\in {\mathbb{R}}^{U\times V}$，对图像$X$进行零填充，两端各补$U-1$和$V-1$个零，得到全填充（Full Padding）的图像$X\in {\mathbb{R}}^{M+2U-2\times N+2V-2}$。图像$X$和卷积核$W$的宽卷积定义为：$$W⨂X\triangleq W⨂X$$其中$⨂$表示宽卷积运算。
  当输入信息和卷积核有固有长度时，他们的卷积依然具有交换性，即$$rot180(W)⨂X=rot180(X)⨂W$$或者$$rot180(W)⨂X=rot180(X)⨂W$$其中$rot180(\cdot )$表示旋转180度。

---

下面给出该公式的证明：
首先给定一个二维图像$X\in {\mathbb{R}}^{M\times N}$和一个二维卷积核$W\in {\mathbb{R}}^{U\times V}$
为了方便证明我们假设$M=N=3，U=V=2$
$$W=\left(\begin{array}{cc}{a}_1& b_1\\ c_1& d_1\end{array}\right)$$$$X=\left(\begin{array}{ccc}{a}_2& b_2& c_2\\ d_2& e_2& f_2\\ g_2& h_2& i_2\end{array}\right)$$
W和X填充后图像为：
$$W=\left(\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& a_1& b_1& 0& 0\\ 0& 0& c_1& d_1& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right)$$$$X=\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& a_2& b_2& c_2& 0\\ 0& d_2& e_2& f_2& 0\\ 0& g_2& h_2& i_2& 0\\ 0& 0& 0& 0& 0\end{array}\right)$$
W和X旋转后图像为：
$$rot180(W)=\left(\begin{array}{cc}{d}_1& c_1\\ b_1& a_1\end{array}\right)$$$$rot180(X)=\left(\begin{array}{ccc}{i}_2& h_2& g_2\\ f_2& e_2& d_2\\ c_2& b_2& a_2\end{array}\right)$$
然后我们计算一下：
等号左边：
$rot180(W)⨂X$ $=rot180(W)⨂X$ $=\left(\begin{array}{cc}{d}_1& c_1\\ b_1& a_1\end{array}\right)$ $⨂$ $\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& a_2& b_2& c_2& 0\\ 0& d_2& e_2& f_2& 0\\ 0& g_2& h_2& i_2& 0\\ 0& 0& 0& 0& 0\end{array}\right)$ $=\left(\begin{array}{ccccc}& a_1{a}_2& b_1{a}_2+a_1{b}_2& b_1{b}_2+a_1{c}_2& b_1{c}_2\\ & c_1{a}_2+a_1{d}_2& d_1{a}_2+c_1{b}_2+b_1{d}_2+a_1{e}_2& d_1{b}_2+c_1{c}_2+b_1{e}_2+a_1{f}_2& d_1{c}_2+b_1{f}_2\\ & c_1{d}_2+a_1{g}_2& d_1{d}_2+c_1{e}_2+b_1{g}_2+a_1{h}_2& d_1{e}_2+c_1{f}_2+b_1{h}_2+a_1{i}_2& d_1{f}_2+b_1{i}_2\\ & c_1{g}_2& d_1{g}_2+c_1{h}_2& d_1{h}_2+c_1{i}_2& d_1{i}_2\end{array}\right)$

等号右边：
$rot180(X)⨂W=rot180(X)⨂W=$ $\left(\begin{array}{ccc}{i}_2& h_2& g_2\\ f_2& e_2& d_2\\ c_2& b_2& a_2\end{array}\right)$ $⨂$ $\left(\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& a_1& b_1& 0& 0\\ 0& 0& c_1& d_1& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right)=$$\left(\begin{array}{ccccc}& a_1{a}_2& b_1{a}_2+a_1{b}_2& b_1{b}_2+a_1{c}_2& b_1{c}_2\\ & c_1{a}_2+a_1{d}_2& d_1{a}_2+c_1{b}_2+b_1{d}_2+a_1{e}_2& d_1{b}_2+c_1{c}_2+b_1{e}_2+a_1{f}_2& d_1{c}_2+b_1{f}_2\\ & c_1{d}_2+a_1{g}_2& d_1{d}_2+c_1{e}_2+b_1{g}_2+a_1{h}_2& d_1{e}_2+c_1{f}_2+b_1{h}_2+a_1{i}_2& d_1{f}_2+b_1{i}_2\\ & c_1{g}_2& d_1{g}_2+c_1{h}_2& d_1{h}_2+c_1{i}_2& d_1{i}_2\end{array}\right)$$

我们可以清晰地看到，原公式等号左边和右边的结果是一样的，即公式$rot180(W)⨂X=rot180(X)⨂W$得证，所以宽卷积具有交换性。

5-3分析卷积神经网络中用1×1的卷积核的作用。

1、跨通道的特征整合

  如果当前层和下一层都只有一个通道那么1×1卷积核确实没什么作用，但是如果它们分别为m层和n层的话，1×1卷积核可以起到一个跨通道聚合的作用，所以进一步可以起到降维（或者升维）的作用，起到减少参数的目的。

  这里通过一个例子来直观地介绍1x1卷积。输入6x6x1的矩阵，这里的1x1卷积形式为1x1x1，即为元素2，输出也是6x6x1的矩阵。但输出矩阵中的每个元素值是输入矩阵中每个元素值x2的结果。

  上述情况，并没有显示1x1卷积的特殊之处，那是因为上面输入的矩阵channel为1，所以1x1卷积的channel也为1。这时候只能起到升维的作用。这并不是1x1卷积的魅力所在。

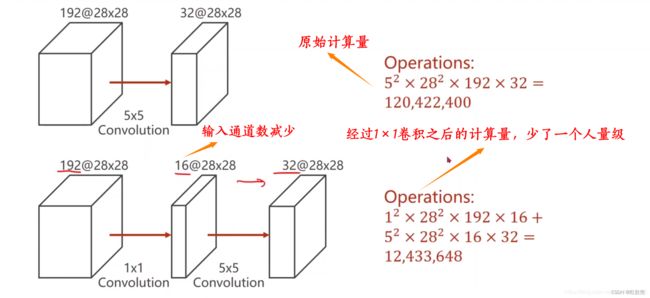
  让我们看一下真正work的示例。当输入为6x6x32时，1x1卷积的形式是1x1x32，当只有一个1x1卷积核的时候，此时输出为6x6x1。此时便可以体会到1x1卷积的实质作用：降维。当1x1卷积核的个数小于输入channels数量时，即降维。

  注意，下图中第二行左起第二幅图像中的黄色立方体即为1x1x32卷积核，而第二行左起第一幅图像中的黄色立方体即是要与1x1x32卷积核进行叠加运算的区域。

其实1x1卷积，可以看成一种全连接（full connection）。
  第一层有6个神经元，分别是a1—a6，通过全连接之后变成5个，分别是b1—b5，第一层的六个神经元要和后面五个实现全连接，本图中只画了a1—a6连接到b1的示意，可以看到，在全连接层b1其实是前面6个神经元的加权和，权对应的就是w1—w6，到这里就很清晰了：

  第一层的6个神经元其实就相当于输入特征里面那个通道数：6，而第二层的5个神经元相当于1x1卷积之后的新的特征通道数：5。w1—w6是一个卷积核的权系数，若要计算b2—b5，显然还需要4个同样尺寸的卷积核。

  上述列举的全连接例子不是很严谨，因为图像的一层相比于神经元还是有区别的，图像是2D矩阵，而神经元就是一个数字，但是即便是一个2D矩阵（可以看成很多个神经元）的话也还是只需要一个参数（1x1的核），这就是因为参数的权值共享。

  注：1x1卷积一般只改变输出通道数（channels），而不改变输出的宽度和高度

2、降维/升维

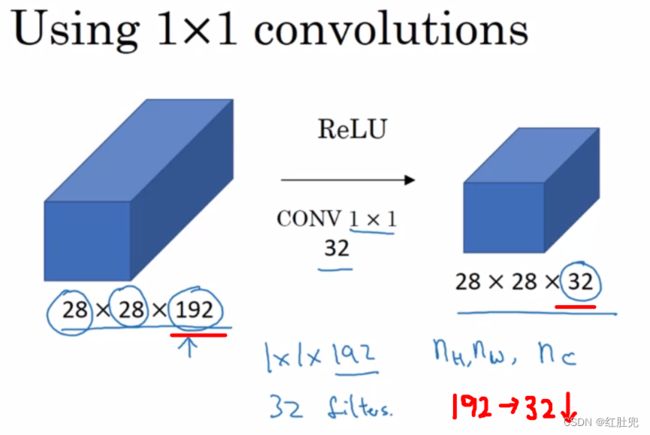
  由于 1×1 并不会改变 height 和 width，改变通道的第一个最直观的结果，就是可以将原本的数据量进行增加或者减少。这里看其他文章或者博客中都称之为升维、降维。但我觉得维度并没有改变，改变的只是 height × width × channels 中的 channels 这一个维度的大小而已

3 、加非线性

  1x1卷积核，可以在保持feature map尺度不变的（即不损失分辨率）的前提下大幅增加非线性特性（利用后接的非线性激活函数），把网络做的很deep。

  备注：一个filter对应卷积后得到一个feature map，不同的filter(不同的weight和bias)，卷积以后得到不同的feature map，提取不同的特征，得到对应的specialized neuron。

4、跨通道信息交互（channal 的变换）

  例子：使用1x1卷积核，实现降维和升维的操作其实就是channel间信息的线性组合变化，3x3，64channels的卷积核后面添加一个1x1，28channels的卷积核，就变成了3x3，28channels的卷积核，原来的64个channels就可以理解为跨通道线性组合变成了28channels，这就是通道间的信息交互。

  注意：只是在channel维度上做线性组合，W和H上是共享权值的sliding window

5、减少计算量

  以下图为例，我们可以看到，计算量明显减少。

5-4对于一个输入为100×100×256的特征映射组，使用3×3的卷积核，输出为100×100×256的特征映射组的卷积层，求其时间和空间复杂度。如果引入一个1×1的卷积核，先得到100×100×64的特征映射，再进行3×3的卷积，得到100×100×256的特征映射组，求其时间和空间复杂度。

  时间复杂度：时间复杂度即模型的运行次数。
  计算公式：$Time\sim O(M^2\ast K^2\ast C_{in}\ast C_{out})$
注：

• M：输出特征图（Feature Map）的尺寸。（默认输入和卷积核的形状是正方形）
• K：卷积核（Kernel）的尺寸。
• Cin：输入通道数。
• Cout：输出通道数。

  空间复杂度：空间复杂度即模型的参数数量。
  计算公式：$Space\sim O(K^2\ast C_{in}\ast C_{out}+M^2\ast C_{out})$

(1)

• 时间复杂度：256×100×100×256×3×3 = 5,898,240,000
• 空间复杂度：256×100×100 = 2,560,000

(2)

• 时间复杂度：64×100×100×256 + 256×100×100×64×3×3 = 1,638,400,000
• 空间复杂度：64×100×100 + 256×100×100 = 3,200,000

5-7忽略激活函数，分析卷积网络中卷积层的前向计算和反向传播是一种转置关系。

 以3x3作为输入，2x2作为输出。即：
    $X=\left(\begin{array}{ccc}{x}_{11}& x_{12}& x_{13}\\ x_{21}& x_{22}& x_{23}\\ x_{31}& x_{32}& x_{33}\end{array}\right)$

    $W=\left(\begin{array}{cc}{w}_{11}& w_{12}\\ w_{21}& w_{22}\end{array}\right)$

    $Y=\left(\begin{array}{cc}{y}_{11}& y_{12}\\ y_{21}& y{+}_{22}\end{array}\right)$

1. 卷积运算的前向传播

(1) 卷积运算：
$\left(\begin{array}{ccc}{x}_{11}& x_{12}& x_{13}\\ x_{21}& x_{22}& x_{23}\\ x_{31}& x_{32}& x_{33}\end{array}\right)$ $⨂$$\left(\begin{array}{cc}{w}_{11}& w_{12}\\ w_{21}& w_{22}\end{array}\right)$ $=\left(\begin{array}{cc}{y}_{11}& y_{12}\\ y_{21}& y_{22}\end{array}\right)$
  其中
$y_{11}=x_{11}\ast w_{11}+x_{12}\ast w_{12}+x_{21}\ast w_{21}+x_{22}\ast w_{22}$
$y_{12}=x_{12}\ast w_{11}+x_{13}\ast w_{12}+x_{22}\ast w_{21}+x_{23}\ast w_{22}$
$y_{21}=x_{21}\ast w_{11}+x_{22}\ast w_{12}+x_{31}\ast w_{21}+x_{32}\ast w_{22}$
$y_{22}=x_{22}\ast w_{11}+x_{23}\ast w_{12}+x_{32}\ast w_{21}+x_{33}\ast w_{22}$
 我们将$X$展开成16x1的形式，同时$Y$也展开得到4x1的形式，即：
$$X=\left(\begin{array}{c}{x}_{11}\\ x_{12}\\ x_{13}\\ x_{21}\\ x_{22}\\ x_{23}\\ x_{31}\\ x_{32}\\ x_{33}\end{array}\right)Y=\left(\begin{array}{c}{y}_{11}\\ y_{12}\\ y_{21}\\ y_{22}\end{array}\right)$$

 我们假设$C⨂X=Y$
 那么很容易得到：
$$C=\left(\begin{array}{ccccccccc}{w}_{11}& w_{12}& 0& w_{21}& w_{22}& 0& 0& 0& 0\\ 0& w_{11}& w_{12}& 0& w_{21}& w_{22}& 0& 0& 0\\ 0& 0& 0& w_{11}& w_{12}& 0& w_{21}& w_{22}& 0\\ 0& 0& 0& 0& w_{11}& w_{12}& 0& w_{21}& w_{22}\end{array}\right)$$
 我们再将$C$定义为$(C_1,C_2,....C_9)$即：
$$C=(C_1,C_2,....C_9)$$$$C_1=\left(\begin{array}{c}{w}_{11}\\ 0\\ 0\\ 0\end{array}\right)C_2=\left(\begin{array}{c}{w}_{12}\\ w_{11}\\ 0\\ 0\end{array}\right)......C_9=\left(\begin{array}{c}0\\ 0\\ 0\\ w_{22}\end{array}\right)$$

(2) 损失函数：

  定义损失函数：$L=loss(y_{11},y_{12},y_{21},y_{22})$

  从$X\to Y\to L$的过程是卷积运算的前向传播过程，这里忽略了偏置项b以及卷积之后的激活函数。

2. 卷积运算的反向传播

(1)计算$X$的梯度
$$\frac{\partial L}{\partial X}=\left(\begin{array}{ccc}\frac{\partial L}{\partial x_{11}}& \frac{\partial L}{\partial x_{12}}& \frac{\partial L}{\partial x_{13}}\\ \frac{\partial L}{\partial x_{21}}& \frac{\partial L}{\partial x_{22}}& \frac{\partial L}{\partial x_{23}}\\ \frac{\partial L}{\partial x_{31}}& \frac{\partial L}{\partial x_{32}}& \frac{\partial L}{\partial x_{33}}\end{array}\right)$$

 其中每一项的梯度：
$\frac{\partial L}{\partial x_{11}}=\frac{\partial L}{\partial y_{11}}\frac{\partial y_{11}}{\partial x_{11}}+\frac{\partial L}{\partial y_{12}}\frac{\partial y_{12}}{\partial x_{11}}+\frac{\partial L}{\partial y_{21}}\frac{\partial y_{21}}{\partial x_{11}}+\frac{\partial L}{\partial y_{22}}\frac{\partial y_{22}}{\partial x_{11}}$

$\frac{\partial L}{\partial x_{12}}=\frac{\partial L}{\partial y_{11}}\frac{\partial y_{11}}{\partial x_{12}}+\frac{\partial L}{\partial y_{12}}\frac{\partial y_{12}}{\partial x_{12}}+\frac{\partial L}{\partial y_{21}}\frac{\partial y_{21}}{\partial x_{12}}+\frac{\partial L}{\partial y_{22}}\frac{\partial y_{22}}{\partial x_{12}}$

$\frac{\partial L}{\partial x_{13}}=\frac{\partial L}{\partial y_{11}}\frac{\partial y_{11}}{\partial x_{13}}+\frac{\partial L}{\partial y_{12}}\frac{\partial y_{12}}{\partial x_{13}}+\frac{\partial L}{\partial y_{21}}\frac{\partial y_{21}}{\partial x_{13}}+\frac{\partial L}{\partial y_{22}}\frac{\partial y_{22}}{\partial x_{13}}$

$\frac{\partial L}{\partial x_{21}}=\frac{\partial L}{\partial y_{11}}\frac{\partial y_{11}}{\partial x_{21}}+\frac{\partial L}{\partial y_{12}}\frac{\partial y_{12}}{\partial x_{21}}+\frac{\partial L}{\partial y_{21}}\frac{\partial y_{21}}{\partial x_{21}}+\frac{\partial L}{\partial y_{22}}\frac{\partial y_{22}}{\partial x_{21}}$

$\frac{\partial L}{\partial x_{22}}=\frac{\partial L}{\partial y_{11}}\frac{\partial y_{11}}{\partial x_{22}}+\frac{\partial L}{\partial y_{12}}\frac{\partial y_{12}}{\partial x_{22}}+\frac{\partial L}{\partial y_{21}}\frac{\partial y_{21}}{\partial x_{22}}+\frac{\partial L}{\partial y_{22}}\frac{\partial y_{22}}{\partial x_{22}}$

$\frac{\partial L}{\partial x_{23}}=\frac{\partial L}{\partial y_{11}}\frac{\partial y_{11}}{\partial x_{23}}+\frac{\partial L}{\partial y_{12}}\frac{\partial y_{12}}{\partial x_{23}}+\frac{\partial L}{\partial y_{21}}\frac{\partial y_{21}}{\partial x_{23}}+\frac{\partial L}{\partial y_{22}}\frac{\partial y_{22}}{\partial x_{23}}$

$\frac{\partial L}{\partial x_{31}}=\frac{\partial L}{\partial y_{11}}\frac{\partial y_{11}}{\partial x_{31}}+\frac{\partial L}{\partial y_{12}}\frac{\partial y_{12}}{\partial x_{31}}+\frac{\partial L}{\partial y_{21}}\frac{\partial y_{21}}{\partial x_{31}}+\frac{\partial L}{\partial y_{22}}\frac{\partial y_{22}}{\partial x_{31}}$

$\frac{\partial L}{\partial x_{32}}=\frac{\partial L}{\partial y_{11}}\frac{\partial y_{11}}{\partial x_{32}}+\frac{\partial L}{\partial y_{12}}\frac{\partial y_{12}}{\partial x_{32}}+\frac{\partial L}{\partial y_{21}}\frac{\partial y_{21}}{\partial x_{32}}+\frac{\partial L}{\partial y_{22}}\frac{\partial y_{22}}{\partial x_{32}}$

$\frac{\partial L}{\partial x_{33}}=\frac{\partial L}{\partial y_{11}}\frac{\partial y_{11}}{\partial x_{33}}+\frac{\partial L}{\partial y_{12}}\frac{\partial y_{12}}{\partial x_{33}}+\frac{\partial L}{\partial y_{21}}\frac{\partial y_{21}}{\partial x_{33}}+\frac{\partial L}{\partial y_{22}}\frac{\partial y_{22}}{\partial x_{33}}$

由于：
  $\frac{\partial L}{\partial x_{ab}}={\sum }_{i=1}^2{\sum }_{j=1}^2\frac{\partial L}{\partial y_{ij}}\frac{\partial y_{ij}}{\partial x_{ab}}$
  $y_{ij}={\sum }_{a=1}^2{\sum }_{b=1}^2{w}_{ab}\ast x_{i+a-1,j+b-1}$
可以得到：
  $\frac{\partial Y}{\partial x_{ab}}=C_{3\ast a+b-3}^T$
所以$$\frac{\partial L}{\partial X}=\left(\begin{array}{c}\frac{\partial L}{\partial x_{11}}\\ \frac{\partial L}{\partial x_{12}}\\ ....\\ \frac{\partial L}{\partial x_{33}}\end{array}\right)=\left(\begin{array}{c}{C}_1^T\\ C_2^T\\ ...\\ C_9^T\end{array}\right)\ast \frac{\partial L}{\partial Y}=C^T\ast \frac{\partial L}{\partial Y}$$
  通过上述的分析，我们很清晰的得到在不考虑激活函数情况下，卷积层的反向传播就是和$C$的转置相乘。

推导CNN反向传播算法

参考文献

1*1卷积核的作用
卷积神经网络(CNN)反向传播算法 - 刘建平Pinard - 博客园 (cnblogs.com)
卷积神经网络(CNN)反向传播算法推导
https://blog.csdn.net/ABU366/article/details/127586130?spm=1001.2014.3001.5502

个人总结

  敲公式敲了半天，本次作业所有公式都是纯手打的，不得不说敲的心烦，眼睛都快瞎了，如果有不对的地方还请指出。对于1x1卷积核的作用也算是有了一个更好更全面的理解，算是长了见识。卷积层的前向计算和反向传播是一种转置关系的证明的公式也是一个一个字打出来的。关于推导CNN反向传播算法手写的字迹不太好看，碍于内容太多，实在不想打字了，还望海涵。