【CNN】经典网络LeNet——最早发布的卷积神经网络之一

前言

LeNet是Yann LeCun于1988年提出的用于数字识别的网络结构，可以说LeNet是深度CNN网络的基石，AlexNet、VGG、GoogLeNet、ResNet等都是在VGG基础上加入各类激活函数或加深网络演变而来的，所以理解LeNet对于现在主流CNN深度学习架构的理解有很大帮助。

关于LeNet详细的介绍可以阅读，《Gradient-Based Learning Applied to Document Recognition》，对LeNet的架构做了详细的介绍，并对LeNet与其他算法做了详细的对比。并且这是第一篇通过反向传播成功训练卷积神经网络的研究。

一，介绍

LeNet主要的出现契机是手写数字的识别，并在邮政和银行发挥了非常重要的角色。但是，这个网络在当时流行度没那么高，但是知名度最高的还是MNIST数据集。

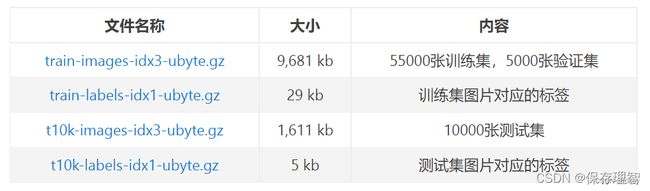
所有的都是黑白图。
对于LeNet,总体来看，LeNet（LeNet-5）由两个部分组成：

• 卷积编码层：由两个卷积层组成
• 全连接密集块：由是哪个全连接层组成

架构图如下图所示：

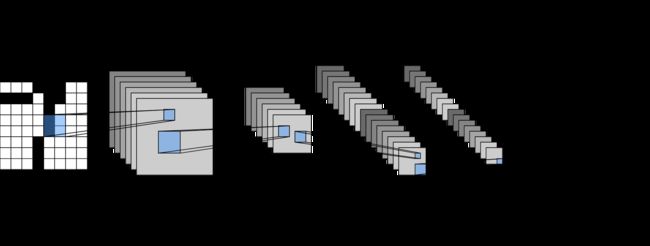
输入的是28 * 28的单通道图片 得到6输出通道的28 * 28的feature map, 通过池化层,得到 6通道 14 * 14的特征图，最后通过卷积操作得到16 输出通道的特征图，在通过池化得到16通道的5 * 5特征图，最后使用三个全连接层，拉成10通道输出，得到0 ~ 9的数字识别结果。
还有一些超参数：

1. 到c1 是: kernel_size = 5,padding = 2.
2. 到s2 是:kernel_size = 5,stride = 2
3. 到c3 是:kernel_size = 5
4. 到s4 是: kernel_size = 2,stride = 2

卷积块中的基本单元是一个卷积层、一个sigmoid激活函数和平均汇聚层，虽然ReLU和最大汇聚层更有效，但它们在20世纪90年代还没有出现。每个卷积层使用卷积核和一个sigmoid激活函数去代替。

对于LeNet是早期成功的神经网络，先使用卷积层来学习图片的空间信息，然后使用全连接层来转换到别的空间。
这个思想，影响了早期神经网络的训练模式，现在几乎不这样。

二，代码实现

按照卷积的计算公式和上面的超参数，通过卷积的输出计算公式搭建网络:

2.1 搭建网络

导入所需要的包

import torch
from torch import nn
import torchvision
from torchvision import transforms
from torch.utils import data
import matplotlib.pyplot as plt
import numpy as np

按照上图图示搭建网络结构

net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

搭建好网络之后，我们需要通过大小为的单通道（黑白）图像通过LeNet。通过在每一层打印输出的形状，我们可以检查模型，以确保其操作与我们期望的。

X = torch.rand(size=(1, 1, 28, 28), dtype=torch.float32)
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__, 'output shape: \t', X.shape)

2.2 模型的训练

现在我们已经实现了LeNet,让我们来看看在Fashion-MNIST数据集上的表现。
先读取对应的数据集：

def load_data_fashion_mnist(batch_size, resize=None):
    """Download the Fashion-MNIST dataset and then load it into memory.
    Defined in :numref:`sec_fashion_mnist`"""
    trans = [transforms.ToTensor()]
    if resize:
        trans.insert(0, transforms.Resize(resize))
    trans = transforms.Compose(trans)
    mnist_train = torchvision.datasets.FashionMNIST(
        root="../data", train=True, transform=trans, download=True)
    mnist_test = torchvision.datasets.FashionMNIST(
        root="../data", train=False, transform=trans, download=True)
    return (data.DataLoader(mnist_train, batch_size, shuffle=True,
                            num_workers=4),
            data.DataLoader(mnist_test, batch_size, shuffle=False,
                            num_workers=4))

设置训练的小批量大小

batch_size = 256
train_iter, test_iter = load_data_fashion_mnist(batch_size = batch_size)

设置超参数和epoches的数量

device = ('cuda' if torch.cuda.is_available() else 'cpu')
net.to(device)
optimizer = torch.optim.Adam(net.parameters(), lr=1e-3)
# 损失函数
loss_func = nn.CrossEntropyLoss()
epoches = 120
costs = []

开始训练

for epoch in range(epoches):
    sum_loss = 0
    net.train()
    for step, (batch_x,batch_y) in enumerate(train_iter):
        # 如果是存在gpu的话，直接使用gpu来训练
        if torch.cuda.is_available():
            batch_x = batch_x.cuda()
            batch_y = batch_y.cuda()
        # 梯度清零
        optimizer.zero_grad()
        output = net(batch_x)
        loss = loss_func(output, batch_y)
        loss.backward()
        optimizer.step()
        if step % 100 == 0:
            costs.append(loss)
            sum_loss += loss
            print(f'epoch:{epoch + 1},mini_batch:{step + 1},mini_loss:{sum_loss / 100}')
            sum_loss = 0.0
    # 验证
    net.eval()
    correct = 0.0
    total = 0
    for(test_x, test_y) in test_iter:
        if torch.cuda.is_available():
            test_x = test_x.cuda()
            test_y = test_y.cuda()
        test_output = net(test_x)
        # 只返回最大数的那个索引
        predicted = torch.max(test_output, 1)[1]
#         计算总数
        total += test_y.size(0)
#     计算预测的正确数目
        correct += (predicted == test_y).sum()
    print(f'correct:{correct}')
    print(f'total:{total}')
    print(f'Test acc:{(correct / total * 100):.2f}%')

绘制损失图与得到最终结论：

if torch.cuda.is_available():
    costs = [cost.cpu().detach().numpy() for cost in costs]
else:
    costs = [cost.numpy for cost in costs]
plt.plot(costs)
plt.xlabel('number of iteration')
plt.ylabel('loss in train')
plt.title('LeNet')
plt.show()

最后得到的loss图示：

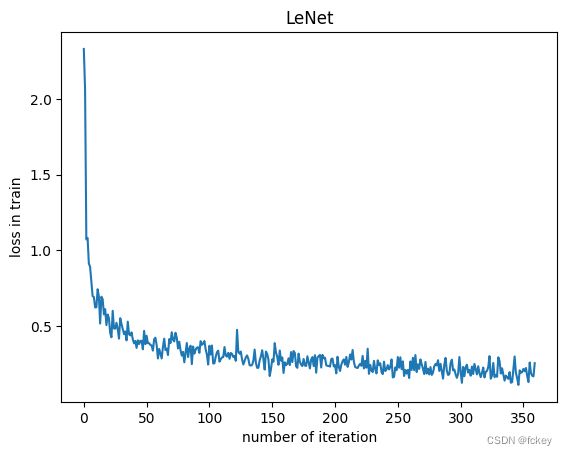
与一般的验证精度：

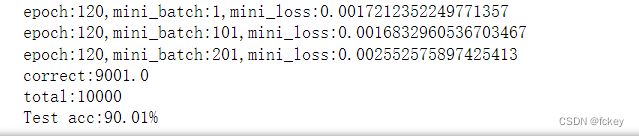
总体来说表现良好。

三，总结

• 卷积神经网络（CNN）是一类使用卷积层的网络。

• 在卷积神经网络中，我们组合使用卷积层、非线性激活函数和汇聚层。

• 为了构造高性能的卷积神经网络，我们通常对卷积层进行排列，逐渐降低其表示的空间分辨率，同时增加通道数。

• 在传统的卷积神经网络中，卷积块编码得到的表征在输出之前需由一个或多个全连接层进行处理。

• LeNet是最早发布的卷积神经网络之一。

---

参考：
https://zh-v2.d2l.ai/chapter_convolutional-neural-networks/lenet.html
https://blog.csdn.net/qq_43960768/article/details/124652618?spm=1001.2101.3001.6650.2&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7ERate-2-124652618-blog-122780852.pc_relevant_multi_platform_whitelistv4&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7ERate-2-124652618-blog-122780852.pc_relevant_multi_platform_whitelistv4&utm_relevant_index=5