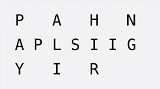算法笔记——每日一题（完结）

此篇以完结：为了抓住面试重点：转向剑指Offer每日一题系列。Click me forward to new article

前言

以前当兵的时候，每次搞30公里强行军都很累。于是我会在50斤的背囊上写着：行百里者半九十——>靠着这句话，即使腿抽筋着，我都能坚持自己完成下来。
现在，我同样用这句话来激励自己，天下没有难学的技术，只有半途而废的人。不要求我一定能成为技术大牛（毕竟这需要一定的天赋和机遇）
旦求无愧于自己。平凡而不平庸即可。

比昨天的自己更好一点，比明天的自己更差一点

初级算法

1、两数之和

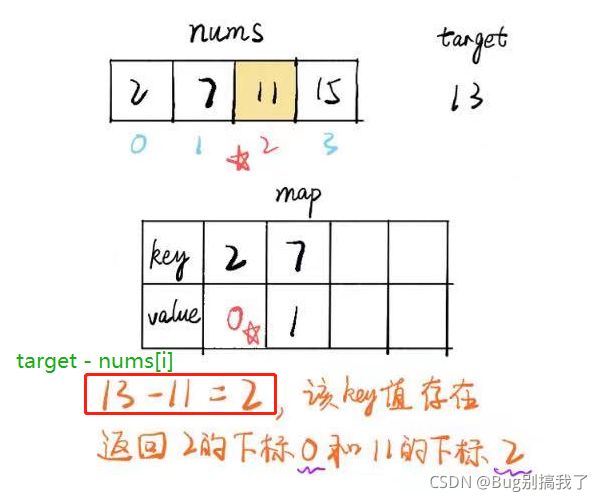
给定一个数组nums，和一个整数目标值target。从数组中找出两个元素，他们的和 = target。
返回对应两个元素的数组下标。

public int[] twoSum(int[] nums, int target){
Map<Integer,Integer> map = new HashMap<>();
for(int i = 0; i < nums.length(); i ++){
// 利用 【Map集合的containsKey API】
//  逆向思维： target = key + nums[i] 
//       ===> map.key = target - nums[i]时 返回结果！
if(map.containsKey(target - nums[i])){
return new int[]{map.get(target - nums[i]), i};
}
}
map.put(nums[i],i);
}
return null;

如果用双层for循环固然简单，但是时间复杂度为O(n^2)
解题思路：

---

7、整数反转

给你一个32位的有符号整数x，返回将x中的数字反转后端结果。
如果反转后的整数超过32位的有符号整数的范围[-2^31, 2^31 - 1]——> 返回 0

public int reverse(int x) {
32位整数范围是：-2147483648 ~ 2147483647
为快速判断：只要将反转后的值，与最大值的最后两个数：十位 / 个位 进行比较即可
1、当反转后的值 大于十位之前的值时：无论它的各位数是几，都是越界的：214748365* 与 2147483647
2、当反转后的值 等于十位之前的值时：判断其个位 是否>最大值的个位：214748364* 与 2147483647
        int res = 0;  // 初始 0
        while(x!=0) {
            每次摘下当前 x 的个位
            int tmp = x%10;
            当摘下->放入 执行到214748364共9位时，即可进行判断
            （如果全部反转完再判断，则会抛出异常）
            因此，反转到最后2个（十位）时，如果大于了最大值的十位，则没必要比较个位了、
            如果反转到十位时，发现和最大值的十位及其之前的数都相等。则需要再反转一次：比较个位
            //判断是否 大于 最大32位整数
            if (res>214748364 || (res==214748364 && tmp>7)) {
                return 0;
            }
            //判断是否 小于 最小32位整数
            if (res<-214748364 || (res==-214748364 && tmp<-8)) {
                return 0;
            }
            // res：当前这一步while反转后的值
            res = res*10 + tmp; 将当前 x 的个位，放入反转后的值的个位中
            //  由于 原值 x 的末尾数字已经被取走：放入res中了。
            // 因此 原值x 就少扣除末尾的那一位。
            x /= 10;
        }
        return res;
    }

---

9、回文数

给你一个整数x，如果x是一个回文整数，返回true。否则返回false。
eg：123不是回文。121是回文
直接StringBuilder.reverse => 但是这样要额外创建对象、并且反转整个字符串来比较
实际上：只要反转x的前半段，然后与后半段比较即可、如11222211; 反转1122—>2211 == 后半段！

    private static boolean test(int x){
        if (x <= 0 || ( x % 10 == 0 && x != 0)){
            return false;
        }
        int revertedNum = 0;
        // 通过 % 和 /的方式，达到string字符串remove的效果
        // eg: 1122332211  ==> 每次从末尾摘除一位，赋给revertedNum后，x就要扣除一位
        // 最后 x = 11223 == revertedNum = 11223 退出循环！
        while (x > revertedNum){
            // 反转后的数 = 上次反转的数 * 10 + 本次 x 的末尾摘下的个位
            revertedNum = revertedNum * 10 + x % 10;
            // 本次x被摘下了个位，于是就x剩下 x / 10;
            // 这样只需要摘除x的一半长度时，即可判断是否为回文数
            x = x / 10;
        }
        // 如果x是奇数：那么退出循环的结果会是 x=1122 revertedNum=11223
        // 所以x == revertedNum / 10 时也为true;
        return x == revertedNum || x == revertedNum / 10;
    }

---

14、最长公共前缀

寻找一个字符串数组中的最长公共前缀，不存在则返回""

    private static String test(String[] arr){
        if (arr.length == 0){
            return "";
        }else if (arr.length == 1){
            return arr[0];
        }
        String commonString = "";
        String first = arr[0];
        int flag = 0;
        for (int i = 0; i < first.length(); i++) {
            for (int j = 1; j < arr.length; j++) {
                if (!arr[j].startsWith(first.substring(0, i))){
                    flag = 1;
                    break;
                }
            }
            if (flag == 1){
                break;
            }
            commonString = first.substring(0, i);
        }
        return commonString;
    }

---

27、移除元素【拷贝复制】

给你一个整数数组、和一个目标值val。移除该数组中所有值等于val的元素。返回移除后的长度。
要求：原地修改数组、不使用额外的空间。

 public static void main(String[] args) {
        int[] nums = {1,2,3,4,5,6};
        System.out.println(removeElement(nums,5));
    }

    private static int removeElement(int[] nums, int val){
        int result = 0;
        for (int i = 0; i < nums.length; i++) {
       //在原数组上：发现与val相同的元素，则跳过
       // 与val不同的元素，则放入数组前面，保存下来。并且长度++
            if (nums[i] != val){
                nums[result] = nums[i];
                result++;
            }
        }
        return result;
    }

---

28、实现strStr()【双指针】

给你两个字符串haystack和needle，请你再haystack字符串中找出needle字符串出现的第一个位置
如果不存在，则返回 -1； 当needle字符串为空时，应该返回0；
这与C语言定义的strStr()函数以及Java定义的indexOf()函数相当
双指针在数组遍历中非常非常地常见

    private static int indexOf(String haystack, String needle){
        int result = 0;
        if (haystack.equals("") || needle.length() > haystack.length()){
            return -1;
        }
        if (needle.equals("")){
            return 0;
        }
        int left = 0, right = needle.length();
        while (right < haystack.length()){
            String substring = haystack.substring(left, right);
            if (substring.equals(needle)){
                return left;
            }
            left++;
            right++;
        }
        return result;
    }

---

35、搜索插入位置

很简单的一题、没啥可说的。
给你一个无重复元素的升序数组、给你一个target、找出target的插入位置。如果已有target则返回索引

    private static int searchInsertPosition(int[] nums, int target){
        if (target < nums[0]){
            return 0;
        }
        if (target > nums[nums.length - 1]){
            return nums.length;
        }
        int left = 0, right = nums.length - 1;
        int mid = 0;
        while (left < right){
            mid = (left + right) / 2;
            if (nums[mid] == target){
                return mid;
            }
            if (nums[mid] < target){
                left = mid + 1;
            }else {
                right = mid - 1;
            }
        }
        return mid;
    }

---

==============================================================================

中级算法

2、两数相加【预先指针】

给你两个【非空】链表，表示两个非负整数。他们的每位数字都是按照【逆序】的方式存储的，
并且每个节点只能存储【一位】数字。
请你将两个数相加，并以相同形式返回一个表示和的链表。
你可以假设除了数字0之外，这两个数都不会以0开头。
示例：l1 = [2, 4, 3] 、 l2 = [5, 6, 4]、 342 + 465 = 708 、、 return [7, 0, 8]

先看看我的解题思路：代码有点复杂
就是用简单的：每一位与每一位相加，>0则往上一位进1。我这里没有给短的List用0补全。
而LetCode大佬的解法是：把短的这个List用0补全——>构造出 l1长度 == l2，然后进行进位运算

	public ListNode addTwoNumbers(ListNode l1,ListNode l2){
	// 用于存储最后结果的list链表
        LinkedList<Integer> list = new LinkedList<>();
        //存储每次要进位的数
        int z = 0;
        //  如果传进来的l1 > l2 则交换一下位置
        if (l1.size() > l2.size()){
            return addTwoNumbers(l2,l1);
        }
        Iterator i1 = l1.iterator();
        Iterator i2 = l2.iterator();
        //  小的链表驱动大的表
        while (i1.hasNext()){
        // 取出l1的尾元素
            int last1 = l1.removeLast();
            // 取出l2的尾元素
            int last2 = l2.removeLast();
            //  计算两之和
            int sum = last1 + last2 + z;
            //  求出余数
            int y = sum % 10;
            //   求出进位的数  18则进位1  即 z = 1
            z = sum / 10;
            //  余数即可放入return的链表中了
            list.add(y);
        }
        //  当小的链表都取完了之后，直接取大的链表剩余的部分即可。 
        for (int i = 0; i < l2.size(); i++) {
            int last = l2.removeLast();
             // 注意也要加上之前余留的进位数 z
            int sum = last + z;
            int y = sum % 10;
            z = sum / 10;
            //  把余数加到return的list中
            list.add(y);
        }
        //  最后，如果进位！=0，则说明还没加完，把最后这个进位加到末尾即可。
        if (y != 0){
            list.add(z);
        }
        return list;
}

---

3、无重复字符的最长子串【滑动窗口】

给定一个字符串s，请你找出其中不含有重复字符的【最长子串】的长度
例如：输入s = “pwwkew” 输出3

//  博主的渣渣解题方法： 时间复杂度为O(m)
    public int getMaxLengthOfString(String s){
        String result = "";
        int max = 1;
        for (int i = 0; i < s.length(); i++) {
            String c = String.valueOf(s.charAt(i));
            System.out.println("char[" + i + "] -->" + c);
            System.out.println("result --pre-->" + result);
            // 判断目前筛选出的无重复字符的字符串result中，是否含有将要比对的这个字符 c
            if (result.contains(c)){
                System.out.println("此次result为" + result + "，发现重复字符：" + c);
                max = Math.max(max,result.length());
                System.out.println("目前筛选出的不重复字符串result的最大长度为：" + max);
                // 重置之前筛选出的result为当前发现的这个重复字符：继续往后筛选比对
                result = c;
                System.out.println("重置result! 重置后的result为：" + result);
            }else {
                System.out.println("当前result中不包含"+ c +"，将" + c + "加入result中...");
                result = result + c;
                System.out.println("result --post-->" + result);
            }
            System.out.println("------------------------------>");
        }
        System.out.println("筛选完毕，返回结果------->");
        return max;
    }

LetCode大佬的【滑动窗口】算法
窗口：内含无重复字符的最长子串。每次找到重复字符，指针滑动到重复字符处！
坚持寻找无重复字符找了好久都没重复！突然发现了一个重复的！前功尽弃！在这里重新开始

    private static int getMaxLengthOfString(String s){
            int n = s.length(), ans = 0;
            //  key为字符 value为下标+1
            // map中存着目前已经扫描到的字符及其下标
            Map<Character, Integer> map = new HashMap<>();
            for (int end = 0, start = 0; end < n; end++) {
                char alpha = s.charAt(end);
                if (map.containsKey(alpha)) {
                // 如果map中已经包含的这个字符：即发现了重复字符
                //  则将起始指针移至重复字符的下标处
                    start = Math.max(map.get(alpha), start);
                }
                // 不包含则将本次的长度置为新的最大长度ans
                ans = Math.max(ans, end - start + 1);
                // 并将本次扫描过的字符放到map中， 以便下次contains比较
                map.put(s.charAt(end), end + 1);
            }
            return ans;
    }

---

5、最长回文子串【动态规划】

给你一个字符串s，找到s中的最长回文子串：即字符串关于中心对称（左=右）
如：s=“babad” return “bab”; s=“cbbd” return “bb”;

解法：动态规划！为减少重复计算：
每次都需要对内层字符串是否为回文串进行重复判断
将内层字符串是否为回文串缓存起来！这样就不用重复判断了
用一个boolean dp[l][r] （类似Redis，缓存着上一次的回文串） 表示字符串从i -> j是否为回文子串。
要判断i->j为回文子串，dp[l][r]=true===>即要判断它的前一位是否为回文子串dp[l-1][r-1]=true

    public String longestPalindrome(String s) {
        // 如果s的长度为1、那回文串就是她本身
        if (s == null || s.length() < 2) {
            return s;
        }
        int strLen = s.length();
        int maxStart = 0;  //最长回文串的起点
        int maxEnd = 0;    //最长回文串的终点
        int maxLen = 1;  //最长回文串的长度

        // 类似redis：缓存着上一轮的最大回文子串
        boolean[][] dp = new boolean[strLen][strLen];
        // r指针从1开始 -> 末尾
        for (int r = 1; r < strLen; r++) {
        // l指针从0开始 -> r   ==> 这样循环下来就能从左到右把所有可能性都遍历一次
            for (int l = 0; l < r; l++) {
                // 如果本次l=r，那么就要看看他们的前一位是否也为回文子串
    // 1.如果r-l<=2即长度为3的时候，那就不用判断dp=true。直接为true！eg：bab
                if (s.charAt(l) == s.charAt(r) && (r - l <= 2 || dp[l + 1][r - 1])) {
                // 判断成功！将本次true记录一下
                    dp[l][r] = true;
        // 并且如果本次长度合法、则记录头指针和尾指针、用于返回最后结果
                    if (r - l + 1 > maxLen) {
                        maxLen = r - l + 1;
                        maxStart = l;
                        maxEnd = r;
                    }
                }

            }

        }
        return s.substring(maxStart, maxEnd + 1);
    }

---

6、Z字形变换

将一个给定字符串s根据给定的行数numRows，从上往下、从左往右进行Z字排序
eg：输入PAYPALISHIRING，numRows=3时。排列为：
之后：将该Z字形排列从左往右逐行读取，产生新的字符串：PAHNAPLSIIGYIR

解答：
何时Z字形字符的方向开始变化！
1、每次在行数 = 0 和 numRows - 1 （即两端处方向发生变换）
2、rowNow = 0 时下一个元素所在行号：为本次行号 + 1，为numRows - 1时：回头：为本次行号 - 1
3、定义一个boolean的flag来标志下一行行号是该 + 1 还是 - 1 ？
用什么数据结构来存储每一行读出的字符？并方便最后结果的拼接？
4、定义一个String类型数组、长度为numRows、数组下标0对应第0行读出的字符、下标1对应第一行

    private static String convert(String s, int numRows){
        if (numRows == 1){
            return s;
        }
        // 这里按道理是直接取(行数)len = numRows，但要考虑特殊情况。
        // 如：s的长度比numRows还小时，直接输出s即可
        int len = Math.min(s.length(), numRows);
        // 声明一个字符串数组：下标为 0 1 2的分别存储第0 1 2行的字符
        // 最后再将这个数组中的字符串依次拼接即可
        String rows[] = new String[len];
        for (int row = 0; row < len; row++) {
            // 先通过for循环把需要的几行数组元素初始化为空串
            rows[row] = "";
        }
        // down为false时，为向右上走(i-1)。true为向下走(i+1)
        boolean down = false;
        // 定义当前所在行
        int rowNow = 0;
        // 开始顺序遍历s字符串：
        for (int i = 0; i < s.length(); i++) {
            // 第0个放第0行中，第1个放第1行...遇到方向变化则回头
            rows[rowNow] += s.charAt(i);
            // 在当前行数为0；或为numRows - 1：即在两端口时，需要变换方向
            if (rowNow == 0 || rowNow == numRows -1){
                down = ! down;
            }
            // 下次循环的行数rowNow是根据转向标志flag来判断是+1还是-1；
            rowNow += down ? 1 : -1;
        }
        // 至此，String数组中每个元素都存着对应下标行读取出的字符
        //  因此把他们从0->len拼接起来即可
        String result = "";
        for (int i = 0; i < len; i++) {
            System.out.println("--第" + i + "行数据为：-->" + rows[i]);
            result += rows[i];
        }
        return result;
    }

---

8、字符串转整数【模拟C/C++中的atoi函数】

1、第一步：丢弃读入字符串无用的前导空格：" 1" => 1
2、第二步：检查下一符号是"+“还是”-"，并作为结果正负的依据：" -1" => -1
3、第三步、读入下一非数字字符，直到到达下一非数字字符，往后的其余字符部分则会忽略：
" -0011231 asdada" => -11231 ———— “words and 987” => “0”：因为第三步未解析到数字，结果为0
4、 如果超过Integer的最大和最小值，则取最大最小值
关键点：如何判断char字符是否为a-z或0-9？根据ASCII码：int 值 = char(x) - ‘0’

public static int myAtoi(String str) {
        int len = str.length();
        // str.charAt(i) 方法回去检查下标的合法性，一般先转换成字符数组
        char[] charArray = str.toCharArray();

        // 1、去除前导空格
        int index = 0;
        while (index < len && charArray[index] == ' ') {
            index++;
        }

        // 2、如果已经遍历完成（针对极端用例 "      "）
        if (index == len) {
            return 0;
        }

        // 3、如果出现符号字符，仅第 1 个有效，并记录正负
        int sign = 1;
        char firstChar = charArray[index];
        if (firstChar == '+') {
            index++;
        } else if (firstChar == '-') {
            index++;
            sign = -1;
        }

        // 4、将后续出现的数字字符进行转换
        // 不能使用 long 类型，这是题目说的
        int res = 0;
        while (index < len) {
            char currChar = charArray[index];
            // 4.1 先判断不合法的情况、通过字符的ACSII码来判断是否是合法数字
            if (currChar > '9' || currChar < '0') {
                break;
            }

            // 题目中说：环境只能存储 32 位大小的有符号整数，
            // 因此，需要提前判断乘以 10 以后是否越界 (本次char作为个位 + res*10为新的结果)
            if (res > Integer.MAX_VALUE / 10 || 
            (res == Integer.MAX_VALUE / 10 && (currChar - '0') > Integer.MAX_VALUE % 10)) {
                return Integer.MAX_VALUE;
            }
            if (res < Integer.MIN_VALUE / 10 || (res == Integer.MIN_VALUE / 10 && (currChar - '0') > -(Integer.MIN_VALUE % 10))) {
                return Integer.MIN_VALUE;
            }

            // 4.2 合法的情况下，才考虑转换，每一步都把符号位乘进去
            // currChar - '0' 的 ASCII码的结果：正好就是数字的值：56(8) - 48(0) = 8
            res = res * 10 + sign * (currChar - '0');
            index++;
        }
        return res;
    }

    public static void main(String[] args) {
        String str = "2147483646";
        int res = myAtoi(str);
        System.out.println(res);

        System.out.println(Integer.MAX_VALUE);
        System.out.println(Integer.MIN_VALUE);
    }

---

11、盛水最多的容器【双层for–>双指针优化】

给你一串数字：int[] arr = {1, 8, 6, 2, 5, 4, 8, 3, 7}; 输出最大水容量 = 49
定义水容量为：两数字间的距离 * Math.min(数字1，数字2) ==> 即：较小的数字影响水的高度

1、简单解法： 双层for循环寻找：时间复杂度O（n^2）
2、考虑是否可以优化双层for？因为双层for是暴力解法，时间比较慢？
==>双指针 ==> 用双指针的话！ 关键点就化为 ⇒ 每次循环结束：改移动哪个指针？

    // 凡是遇到【双层for循环的问题】==>考虑是否可用【双指针优化】
    private static int test(int[] arr){
        int capacity = 0;
        int len = arr.length;
        int i = 0, j = len - 1, hi = 0, hj = 0;
        // 从左右两边两个指针往中间遍历，时间复杂度O(n)。双层for则是O(n^2)
        while (i < j){
            hi = arr[i];
            hj = arr[j];
            capacity = Math.max(capacity, (j - i) * Math.min(hi,hj));
            // 这是一个数学规律：由水容量公式 = h * Math.min(hi,hj)
            // 因此，只要移动本次较短的那个木板，因为是他限制了我的水容量
            // 移动短的木板，尝试去找到比他更长的木板来提升水容量！
            // 假设移动的是较长的木板，两种情况：
            // 1.长木板找到更长的！但水容量是由短木板限制的，
            // Math.min(hi,hj)不变，而水桶宽度缩短 ==>必然造成水容量下降！
            // 2.长木板找到比原先更短或一样长的！new Hight <= old Hight
            // 而水桶宽度缩短 ==> 水容量也必然下降
            ===> 因此，这就是我们要找的条件：【每次循环结束：该移动较短的木板】
            if (hi > hj){
                j --;
            }else {
                i ++;
            }
        }
        return capacity;
    }

---

15、三数之和【排序+双指针】

给你一个数组nums = [-1,0,1,2,-1,-4]； 找出三数之和 = 0；并且不重复的所有组合
输出：[[-1,-1,2],[-1,0,1]]；

关键点：1、将数组进行排序–>因为三数之和=0；要求有负有正，L < R
2、 三个数：固定一个数！剩余两个数使用双指针！
3、左右指针：何时移动左、何时移动右。

    public static List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> ans = new ArrayList();
        int len = nums.length;
        if(nums == null || len < 3) {
            return ans;
        }
        Arrays.sort(nums); // 排序
        for (int i = 0; i < len ; i++) {
            if(nums[i] > 0) {
                break; // 如果当前数字大于0，则三数之和一定大于0，所以结束循环
            }
   //每一轮循环定下first第一个数后。
   // 就会将它后面的L(i+1) ~ R(len-1)范围内，所有符合条件的组合都筛选出来！
   // 假设i=0时。值为 -1。那么所有满足L+R+i(value)=0的组合就已经在本次循环查出来了！
   // i=1时，值如果和上一次i(i=0)相同，本次循环i=1 < i=0。L和R的检索范围小于上一次的范围
   // 由于上一次已经查出了所有满足条件的组合。因此这一次范围更小的循环必然重复
            if(i > 0 && nums[i] == nums[i-1]) {
                continue; // 去重
            }
            int L = i+1;
            int R = len-1;
            while(L < R){
                int sum = nums[i] + nums[L] + nums[R];
                if(sum == 0){
                    // 如果本次满足要求。则添加到结果中
                    ans.add(Arrays.asList(nums[i],nums[L],nums[R]));
//这里为什么是这样去除L和R的重复值的？
// while(L
// 在第一个数i 相同的情况下。L和R只要有一个数确定了，另一个数也就确定了！
// 也就是说，本次循环i是相同的，只要L和R有一个数重复了，那么结果必然重复！因此L R都需要去重

                    // 为了下一次计算出的sum不是重复值！要将L指针移动到下一个非重复值处
                    while (L<R && nums[L] == nums[L+1]) {
                        L++; // 去重
                    }
                    // 为了下一次计算出的sum不是重复值！要将R指针移动到下一个非重复值处
                    while (L<R && nums[R] == nums[R-1]) {
                        R--; // 去重
                    }
                    L++;
                    R--;
                }
                // 本轮总和<0，说明正数要多一些 即L++
                else if (sum < 0) {
                    L++;
                    // 本轮总和>0，说明正数要少一些 即R--
                } else if (sum > 0) {
                    R--;
                }
            }
        }
        return ans;
    }

---

16、最接近的三数之和【排序+双指针】

给的一个数组nums(lenth > 3)和target。找出nums中最接近target的三个数的和
eg：nums = [-1,2,1,-4] target = 1。返回结果： 1

解法：同题：15

       public static int threeSum(int[] nums,int target) {
        Arrays.sort(nums); // 排序
        int distance = Math.abs(target - nums[0] + nums[1] + nums[2]);
        int result = 0;
        for (int i = 0; i < nums.length ; i++) {
            int L = i+1;
            int R = nums.length-1;
            while(L < R){
                int now = nums[i] + nums[L] + nums[R];
                if(Math.abs(target - now) < distance){
                    // 如果本次满足要求
                    distance = Math.abs(target - now);
                    result = now;
                    L++;
                    R--;
                }
                // 本轮总和
                else if (now < target) {
                    L++;
                    // 本轮总和>target，说明正数要少一些 即R--
                } else if (now > target) {
                    R--;
                }
            }
        }
        return result;
    }

---

17、电话号码的数字组合【回溯递归】

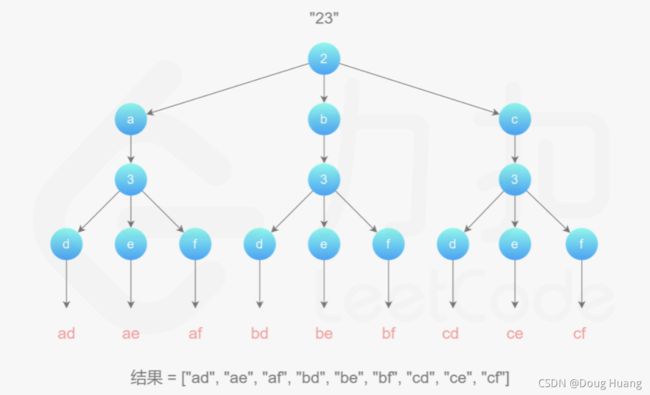
给定一个数字组合（2-9）：输出其所有的字母组合
根节点为2时、对应有a、b、c、三个子节点。三个子节点又都拥有d e f 子子节点

时间复杂度：O(3^m ✖ 4^n)

    private static List<String> result = new ArrayList<String>();
    private static StringBuilder combination = new StringBuilder();
    private static Map<Character, String> phoneMap = new HashMap<Character, String>() {{
        put('2', "abc");
        put('3', "def");
        put('4', "ghi");
        put('5', "jkl");
        put('6', "mno");
        put('7', "pqrs");
        put('8', "tuv");
        put('9', "wxyz");
    }};

    public static void main(String[] args) {
        System.out.println(letterresult("23"));
    }

    public static List<String> letterresult(String digits) {
        // 排空
        if (digits.length() == 0) {
            return result;
        }
        // 回溯：递归调用。
        backtrack(digits, 0);
        return result;
    }

    private static void backtrack(String digits, int index) {
        // 如果本次已经检索到最底层了！eg：23 length=2 index = 2时，
        // 说明是第三层目录了。而总共就两层，所以这次应该回溯
        // 即满足回溯条件。则输出这次结果 result.add
        if (index == digits.length() && combination != null) {
            System.out.println("达到底层，返回结果：" + combination.toString());
            result.add(combination.toString());
        } else {
            char digit = digits.charAt(index); // "23" -> 拿到 2
            String letters = phoneMap.get(digit); //  拿到2对应的字母abc
            int lettersCount = letters.length(); // abc的长度为3
            for (int i = 0; i < lettersCount; i++) { // 以abc为一级目录进行树形搜索
                System.out.println("添加前：" + combination.toString());
                System.out.println("添加combination：" + letters.charAt(i));
                combination.append(letters.charAt(i)); // 把a(本次层级)添加进combination
                System.out.println("添加后：" + combination.toString());
                // 递归调用时、又会遍历index = 1 即二级目录:"3"
                // 对应字母def。将d e f分别与a组合。 combination.append(letters.charAt(i));
                // 得出 ad ae af
                backtrack(digits, index + 1);
                //  --> a的分支(共两层)遍历完后，会在第三层时判断满足条件，回溯 result.add(combination.toString());
                // 从而：本分支backtrack方法递归结束了，此时执行下一步: deleteCharAt只删除本层(index)。保留父层级
                System.out.println("清空前：" + combination.toString());
                combination.deleteCharAt(index);
                System.out.println("清空后：" + combination.toString());
            }
        }
    }

---

18、四数之和【排序+双指针】

给你n个整数组成的数组nums、和一个目标值target！找出满足条件的四元数组！
条件：1、a b c d各不相同。2、nums[a] + nums[b] + nums[c] + nums[d] == target
eg：输入nums = [1, 0, -1, 0, -2, 2]。target = 0
输出：[[-2, ,1, 1, 2], [-2, 0, 0, 2], [-1, 0, 0, 1]]

参照第16题

    public static void main(String[] args) {
        int[] arr = {1,0,-1,0,-2,2};
        test(arr,0).forEach(System.out::println);
    }

    private static List<List<Integer>> test(int[] nums, int target){
        List<List<Integer>> result = new ArrayList<>();
        int len = nums.length;
        if (nums == null || len <= 3){
            return null;
        }
        Arrays.sort(nums);

        for (int i = 0; i < len - 3; i++) {
            if(nums[i] > 0) {
                break;
            }
            if (i > 0 && nums[i] == nums[i-1]){
                continue;
            }
            int LL = i + 1;
            for (; LL < len - 2; LL++) {
                if (LL > 0 && nums[LL] == nums[LL-1]){
                    continue;
                }
                int L = LL + 1;
                int R = len - 1;
                while (L < R){
                    int sum = nums[i] + nums[LL] + nums[L] + nums[R];
                    if (sum == target){
                        result.add(Arrays.asList(nums[i],nums[LL],nums[L],nums[R]));
                    }
                    if (nums[L] == nums[L + 1]){
                        L++;
                    }
                    if (nums[R] == nums[R - 1]){
                        R--;
                    }
                    //注意！移动双指针中L或R指针 的条件是什么？
                    if (target > sum){
                        L++;
                    }else {
                        R--;
                    }
                }
            }
        }
        return result;
    }

---

19、删除链表的倒数第n个节点【巧妙的双指针】

删除链表的倒数第n个节点（注意：我们不知道链表的长度、
链表不像数组集合ArrayList那样，可以通过索引直接删除，链表可不行）

思路：L和R指针初始时，为一个new出来的空节点。指向链表头节点。
1、先移动R指针。移动n次。而后同时移动L和R，直至R到达链表末尾：R.next == null;
——>这样一来：保证了L指针和R指针之间间隔了n个节点。那么当R为尾节点时：L.next就是要删除的节点

private static ListNode removeNthFromEnd(ListNode head, int n){
        if (head == null){
            return null;
        }
        ListNode pointer = new ListNode(0);
        pointer.next = head;
        //初始化左右两个节点。使其指向头结点
        ListNode L = pointer, R = pointer;
        while (n != 0){
        //单独移动R指针，移动n次。
            R = R.next;
            n--;
        }
        此时L.next就是以R开始的倒数第n个节点
        // 将R和L同时移动，直至R为尾节点
        while (R.next != null){
            R = R.next;
            L = L.next;
        }
        //此时：L所指节点L.next即为倒数第n位。删除L指向的节点
        L.next = L.next.next;
        //不能返回pointer，要返回pointer.next。
        //head头结点可能会当成第n个删除。所以不能直接返回head（虽然pointer.next指的就是head）
        return pointer.next;
    }
    static class ListNode {
        int val;
        ListNode next;   // 下一个节点
        ListNode(int x) { val = x; }  //赋值
    }

---

20、有效的括号【栈的使用】

给定一个只包含(){}[]的字符串s。判断字符串是否有效：
左右相同类型的括号要闭合。【必须以正确的顺序闭合】

正确顺序闭合？——> 内层的需要先闭合完、外层才能闭合！
——>很容易想到使用数据结构：栈！
先进后出。先出现的左符号（即外层的）、要放在栈底、等后出现的左符号（内层）闭合完！
再轮到栈底（外层的符号）弹出，然后判断是否闭合！——即：按顺序闭合

    public static boolean test(String s){
    // 排除特殊情况
        if (s.length() == 0 || s.length() % 2 != 0){
            System.out.println("s的长度为0、或长度不为偶数：返回false");
            return false;
        }
        // 用哈希表存储字符的映射规则
        Map<Character,Character> map = new HashMap();
        map.put('[',']');
        map.put('{','}');
        map.put('(',')');
        // 定义一个栈
        Stack<Character> stack = new Stack();
        // 遍历字符串
        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            
           1、如果碰到右闭合符！则不压入、pop出栈顶、判断是否闭合
            // 相当于数据结构算法中学过的：碰到运算符+-*/()等优先级高的字符，则出栈。
            if (c == ']' || c == '}' || c == ')'){
            // 如果第一个字符就为右闭合符：则此时stack中还未push。为null。返回false
                if(stack == null){
                    return false;
                }
                // 如果pop出的左闭合符和对应的右闭合符不匹配。则返回false
                if (map.get(stack.pop()) != c){
                    return false;
                }
            }else {
            2、否则：是左闭合符：入栈
                stack.push(c);
            }
        }
        return true;
    }

---

21、合并两个有序链表【递归】***

将两个有序链表（非递减链表）合并为一个升序链表
【方法一】：递归：在原链表上合并。不新增链表。
递归要素：终止条件：l1或 l2为空时。
递归的理解：不用一步步去想中间的递归步骤。会绕晕的！
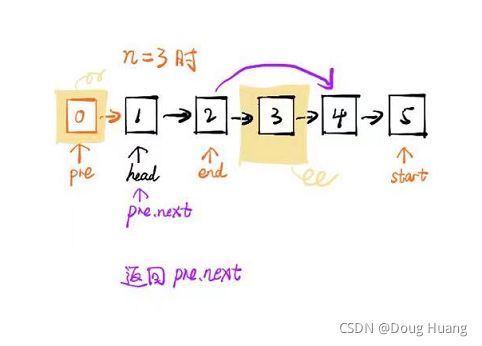
我们只看递归的最后一步：即递归出口的地方。本题中的倒数第二轮递归判断出：
(Node：4.val < Node：5.val)：因此走：head2.next = mergeList(head1, head2.next);
head2：节点4、head2.next：节点4的next指针：即【连接线】
将head2.next（即null）作为最后一轮递归方法mergeList中的参数2传进去（ListNode head2）
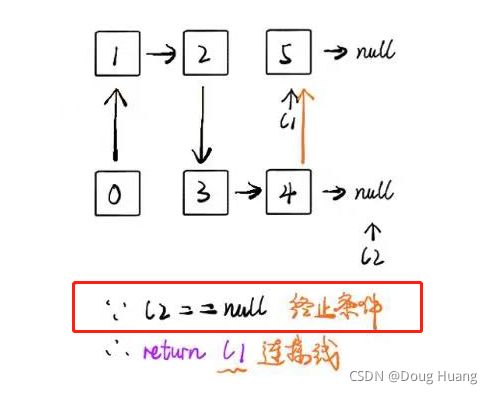
因为head2.next 为 null。即最后一轮递归中。判断出head2 == null。
此处：递归结束！return head1;。而head1即为节点5。return节点5到上一轮递归方法的结果中————>①
于是上一轮递归方法head2.next = mergeList(head1, head2.next);就化为：【head2.next = 节点5】
即图中红色箭头的那根线：节点4指向节点5。
由于找到了出口。代码head2.next = mergeList(head1, head2.next); 执行完毕。
就执行下一行：return head2; ———————————————————————————————>②
而head2不就是本次倒数第二轮递归的节点4吗？最后一轮递归找到了出口：return节点5（①）。
并组成了合并后的有序链表：4 -> 5。节点4即为排好序的链表的头结点！
因此这里return head2（②）; 即返回了排好序的链表的头结点：4
关键在于：从递归的最后一步（出口处）开始分析。只有最后一步找到出口return后，每一轮的递归方法才会执行完毕得到返回值，从而每轮的递归方法才能结束。如果找不到出口。就会一直递归下去。

    public static ListNode mergeList(ListNode head1, ListNode head2){
        if (head1 == null){
            return head2;
        }
        if (head2 == null){
            return head1;
        }
        if (head1.val < head2.val){
        // head1.next即为head1的连接线！
        // 因为head1是本轮中，较小的值。因此他就作为本轮的头结点。
        // 即：【本轮较小的节点head1作为头结点：指向已合并好的链表的头】
        // 一直递归下去：mergeList递归出口就是l1或l2为null时。
        // mergeList即合并好的有序链表。每次递归都让本次较小的节点与排好序的链表头相连！
            head1.next = mergeList(head1.next, head2);
            return head1;
        }else {
            head2.next = mergeList(head1, head2.next);
            return head2;
        }
    }
    
    static class ListNode{
        private int val;
        private ListNode next;
        public ListNode(){}
        public ListNode(int value){
            this.val = value;
        }
    }

方法二：不用递归。用新的一个链表来存储结果（也就是第23题：合并K个升序链表所使用的方法）

 public static ListNode mergeList(ListNode head1, ListNode head2){
       if (head1 == null || head2 == null){
           return head1 == null ? head2 : head1;
       }
       // 新链表的 哑元节点
       ListNode head = new ListNode(0);
       // 指针
       ListNode pointer = head, first = head1, second = head2;
       while (first != null && second != null){
           if (first.val < second.val){
               pointer.next = first;
               first = first.next;
           }else {
               pointer.next = second;
               second = second.next;
           }
           pointer = pointer.next;
       }
       pointer.next = (first == null ? second : first);
       return head.next;
    }

---

22、括号生成【深度优先遍历 + 回溯递归】

这题有点类似17题电话号码的递归实现
根节点为 （ 时。子节点可能为 （ 或 ）、依次递归寻找合法的子节点所构成的树
设n为()括号的数量。根据给定的n。返回出所有合法的括号组合

private static List<String> result = new ArrayList<>();

    public static void main(String[] args) {
        test(2).forEach(System.out::println);
    }

    public static List<String> test(int n){
        // 排除特殊情况
        if (n == 0){
            return null;
        }
        //调用递归方法
        dfs("", 0, 0, n);
        return result;
    }

    // left right分别表示已使用的“(” 和 “)”的数量。  current表示本递归分支中括号的组成结果
    private static void dfs(String current, int left, int right, int n){
        // 递归出口：left和right的使用数都达到n，则结束
        if (left == n && right == n){
            result.add(current);
            return;
        }
        // 如果当前left
        //  即：将本二叉树的分支剪掉
        if (left < right){
            return;
        }
        // 如果 ( 还有可用数、则加入一个 (
        if (left < n){
            dfs(current + "(", left + 1, right, n);
        }
        if (right < n){
            dfs(current + ")", left, right + 1, n);
        }
    }

n=2时——> 结果：

---

24、两两交换链表中的节点【回溯递归】

给定一个链表，两两交换其中相邻的节点，并返回交换后的链表！
注意：要确实去交换节点。而不是交换节点的值。

    public static void main(String[] args) {
        ListNode list1 = new ListNode(1);
        list1.next = new ListNode(2);
        list1.next.next = new ListNode(3);
        list1.next.next.next = new ListNode(4);

        StringBuilder sb = new StringBuilder();
        sb.append("head");
        ListNode listNode = exchangeTwoNode(list1);
        // 输出结果
        while (listNode != null) {
            sb.append( "->" + listNode.val);
            listNode = listNode.next;
        }
        System.out.println(sb);
    }
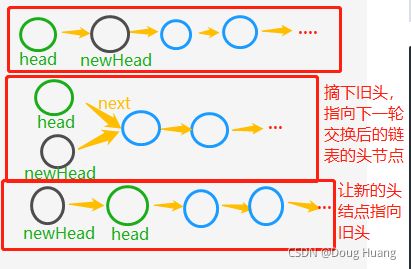
                          【交换方法】
    private static ListNode exchangeTwoNode(ListNode head){
        // 当前无节点，或只有一个节点时：无法交换，直接原样返回
        if (head == null || head.next == null){
            return head;
        }
        // head的next就是交换后的新head（先把旧头结点摘下来）
        ListNode newHead = head.next;
        // 下一轮要交换的链表是newHead.next ==>
        // 即、把：head.next.next（旧的尾节点所指向的那个节点：即为下一轮要交换的链表的链表头）
        // 作为下一轮要交换的链表头，传入递归方法。
        // 让head指向 -> 交换后的链表。
        head.next = exchangeTwoNode(newHead.next);
        // 新的头结点的 指针 -> 指向尾节点（旧头）
        newHead.next = head;
        // 返回新头结点
        return newHead;
    }

    static class ListNode{
        private int val;
        private ListNode next;
        public ListNode(int value){
            this.val = value;
        }
    }

---

29、两数相除【移位运算】

给定两个整数，被除数dividend和除数divisor。将两数相除，要求不使用乘法、除法和mod运算符。
返回被除数dividend除以除数divisor得到的商。
整数触发的结果应当截取其(truncate)小数部分。例如truncate(8.345) = 8
这题LeetCode用了移位运算来实现➗2。以下是我的解法，移位运算不想了解她了

    private static int truncate(int dividend, int divisor){
        long result = 0;
        int last = 0;
        // 默认为正数
        boolean flag = true;
        if ((dividend < 0 && divisor > 0) || (dividend > 0 && divisor < 0)){
            flag = false;
        }
        dividend = Math.abs(dividend);
        divisor = Math.abs(divisor);
        while (last + divisor< dividend) {
            last += divisor;
            result++;
        }
        if (result >= Integer.MAX_VALUE){
            if (flag){
                return Integer.MAX_VALUE;
            }else {
             return Integer.MIN_VALUE;
            }
        }
        return flag ? (int)result : (int)-result;
    }

---

31、下一个排列

实现获取【下一个排列】的函数、算法需要将给定的数字序列重新排列成字典序中下一个更大的排列。
——>即：组合出下一个更大的整数
如果不存在下一个更大的排列，则将数组重新排列成最小的排列（即升序排列）
必须【原地】修改，允许使用额外的常数空间
eg：输入nums = [1, ,2, 3] 输出：[1, 3, 2]
关键在于：对【下一个排列】的理解

    public static void main(String[] args) {
        int[] param = {1,2,3,8,5,7,6,4};
        int[] result = nextSorted(param);
        for (int i : result) {
            System.out.print(i + " ");
        }
    }
    public static int[] nextSorted(int[] nums){
    // 特殊校验
        if (nums.length <= 1){
            return null;
        }
        // minIndex记录着需要交换的值往右的数组中：比它大的最小的数
        //eg:图中需要交换的值是：5。5往右的数组中，6和7都比他大、但是6是比他大的最小的数
        // 因此6所在的索引就存入minIndex、将来6就会和5进行交换
        int minIndex = -1;
        // 是否找到满足条件的值
        boolean flag = false;
        // 从后往前遍历：nums[i]为当前需要比较的值
        for (int i = nums.length - 2; i > 0; i--) {
        // 遍历i 往右的数组
            for (int j = i + 1; j < nums.length - 1; j++) {
            // 如果找到了比 nums[i]大的数、
                if (nums[j] > nums[i]){
                // 比较本轮数组中找出的比他大的数 是否 < 上一轮找出的比他大的数？
                // 是：把本轮找出的数的索引存入、  否：保持原样
                // 这里需要判断minIndex==-1?  即：是否是第一次找到比nums[i]大的数
                    minIndex = Math.min(nums[j], minIndex == -1 ? nums[j] : nums[minIndex]) == nums[j] ? j : minIndex;
                    // 条件已满足！
                    flag = true;
                }
            }
            // 如果条件满足，交换值
            if (flag){
                // 交换值
                int temp = nums[i];
                nums[i] = nums[minIndex];
                nums[minIndex] = temp;
                // 为本轮i往右的数组进行排序--> 
                // 注意 这里sort(a,fromIndex,toIndex)：这个to需要实际的toIndex + 1
                // 因为源码实际调用时 toIndex-1 了：DualPivotQuicksort.sort(a, fromIndex, toIndex - 1, null, 0, 0);
                Arrays.sort(nums,i + 1, nums.length);
                // return
                return nums;
            }
        }
                // 如果找不到下一个排列、则将数组重新以升序排序
        Arrays.sort(nums);
        return null;
    }

---

33、搜索旋转排序数组

一个元素互不相同的整数递增的数组nums、在传递给函数前会在随机一个下标k处进行旋转、
然后再传递给函数、请你在传递后的数组中、找出给定的目标值target。
解题关键点：有序数组的查询、必然是用二分查找、那么这个数组被旋转过、仍然可用二分查找吗？
当然是可以的！思路在于：每次确定二分查找的mid时、左边的数组和右边的数组总有一个是有序数组
通过左边或右边的有序数组和target的比较、就能确定下次二分查找该往哪边进行
eg：nums = {0，1，2，4，5，6，7}。在下标k=3处旋转后，nums = {4，5，6，7，0，1，2}

    private static int searchSpinSortedArray(int[] nums, int target){
        int len = nums.length;
        if (len == 0){
           return -1;
       }
        int left = 0, right = len - 1;
       while (left <= right){
            int mid = (right - left) / 2;
            if (nums[mid] == target){
                return mid;
            }
            // 接下来判断下一轮二分查找该往mid的左边找、还是右边找
            //如果mid的左边是有序数组
            if (nums[0] <= nums[mid]){
                // 并且target的值在mid左边的有序数组内
                if (nums[0] <= target && target < nums[mid]){
                    right = mid - 1;
                }else {
                    left = mid + 1;
                }
            }else
            // 如果0>mid的值：说明mid的右边才是有序数组
            {
                // 并且target值在mid右边的有序数组范围内
                if (nums[mid] < target && target <= nums[left - 1]){
                    left = mid + 1;
                }else {
                    right = mid - 1;
                }
            }
       }
       return -1;
    }

---

34、在排序数组中找出目标元素第一个和最后一个出现的位置。

没啥好说的、一个简单的二分查找法。

public static void main(String[] args) {
        int[] param = {5,7,7,8,8,10};
        for (int i : getFirstAndLast(param, 8)) {
            System.out.print(i + " ");
        }
    }
    private static int[] getFirstAndLast(int[] nums, int target){
        int[] result = {-1,-1};
        int len = nums.length;
        if (len == 0 || target < nums[0]){
            return result;
        }
        int left = 0, right = len -1;
        for (int i = 0; i < len; i++) {
            int mid = (right + left) / 2;
            if (target == nums[mid]){
                int temp = mid;
                result[0] = mid;
                result[1] = mid;
                while ((mid - 1) >= 0 && nums[mid] == nums[mid - 1]){
                    result[0] = mid - 1;
                    mid--;
                }
                while ((temp + 1) < len && nums[temp] == nums[temp + 1]){
                    result[1] = temp + 1;
                    mid++;
                }
                break;
            }
            if (target <= nums[mid]){
                right = mid - 1;
            }
            if (target > nums[mid]){
                left = mid + 1;
            }
        }
        return result;
    }

---

36、有效数独

判断输入的9x9数独是否有效：（没有数字的格子用" . "表示）
1、同一行1-9数字只能出现一次
2、同一列1-9数字只能出现一次
3、每个3X3方格中、1-9数字只能出现一次
类似第6题：Z字形变换。这种图形化的参数传递进来、都需要用某种数据结构来表示他。
这里用的是矩阵来表示

private static boolean judgeEffective(char[][] board) {
//每一行1-9数字是否出现
        int[][] row = new int[9][10];
        //每一列1-9数字是否出现
        int[][] col = new int[9][10];
        //每一个方格中1-9数字是否出现
        int[][] box = new int[9][10];
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                int current = board[i][j] == '.' ? -1 : board[i][j] - '0';
                // 如果当前格子没有数字、则继续下一次循环。
                if (current == -1) {
                    continue;
                }
                //判断在当前行是否出现过
                if (row[i][current] != 0) {
                    return false;
                }
                //判断在当前列是否出现过
                if (col[j][current] != 0) {
                    return false;
                }
                //判断在当前方格是否出现过
                if (box[i + 1 + j / 3][current] != 0) {
                    return false;
                }
                // 都没出现过、则本轮有效、出现次数+1
                row[i][current] = 1;
                col[j][current] = 1;
                box[i + 1 + j / 3][current] = 1;
            }
        }
        return true;
    }

---

38、外观数列【递归】

外观数列的第一项：n=1时、值是1
第二项：11 ——> 一个1
第三项：21 ——> 两个1
第四项：1211 ——> 一个2一个1
第五项：111221 ——> 一个1一个2两个1
每一项都是对前一项的描述：可以看成一种由递归公式组成的数列。
显然、这一题用递归解决

    public static void main(String[] args) {
        System.out.println(countAndSay(5));
    }

    private static String countAndSay(int n){
    // 递归出口：n=1时、值为1
        if (n == 1){
            return "1";
        }
        //递归拿到n的前一项的值：对前一项的描述就是本项的结果、本项的结果又返回给下一项
        String lastResult = countAndSay(n - 1);
        int first = 0;
        List<String> temp = new ArrayList<>();
        // 将前一项按相同连续字符划分成多个字符串组
        for (int i = 0; i < lastResult.length(); i++) {
            if (i + 1 == lastResult.length()){
                temp.add(lastResult.substring(first));
                break;
            }
            if (lastResult.charAt(first) == lastResult.charAt(i + 1)){
                continue;
            }
            temp.add(lastResult.substring(first, i + 1));
            first = i + 1;
        }
        String result = "";
        //对划分出的字符串组进行描述：几个几？ length()个charAt(0)
        for (int i = 0; i < temp.size(); i++) {
            result += temp.get(i).length() + String.valueOf(temp.get(i).charAt(0));
        }
        return result;
    }

---

300、最长递增子序列【动态规划】

给你一个不重复的数组、求该数组的最长递增子序列的长度
递增子序列：严格按照递增的顺序排列

方法一（动态规划）：

    public static void main(String[] args) {
        int[] param = new int[8];
        param[0] = 2;
        param[1] = 5;
        param[2] = 7;
        param[3] = 8;
        param[4] = 6;
        param[5] = 9;
        param[6] = 10;
        param[7] = 18;
        System.out.println(lengthOfLIS(param));
    }

    public static int lengthOfLIS(int[] nums) {
        if(nums.length == 0) return 0;
        // dp[i]存的是nums数组中、以索引i为结尾的最长递增子序列的 长度！
        // 此dp[i]存的不是当前找到的最长递增子序列、不是严格递增的。因此不能二分
        int[] dp = new int[nums.length];
        int res = 0;
        Arrays.fill(dp, 1);
        for(int i = 0; i < nums.length; i++) {
            // 与i之前的各个值nums[j]进行比较
            for(int j = 0; j < i; j++) {
            // 如果nums[i]比值nums[j]大、
            // 则下标为i时的最长子序列长度、就可以在索引为j时的长度基础上 + 1
                if(nums[j] < nums[i]) dp[i] = Math.max(dp[i], dp[j] + 1);
            }
            res = Math.max(res, dp[i]);
        }
        return res;
    }

方法二（动态规划 + 二分查找）（时间复杂度 O(n·logn)）：

    public static int lengthOfLIS(int[] nums){
        // 此dp存储：当前找到的最长递增子序列
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        int x = 0;
        for (int i = 1; i < nums.length; i++) {
            // 如果num比dp[x]小（如果num比之前的递增子序列的最大值更小）
            if (nums[i] < dp[x]){
                // 如果nums[i]比dp[x]小 且比dp[x]里其他的数大（满足递增条件）、才能覆盖
                // 由于dp[x]存的是严格递增的子序列、因此可以用二分法
                int left = 0;
                while (left < x){
                    int m = (x + left) / 2;
                    //若 中间数仍小于num：下一次在右半区间比较
                    if (dp[m] < nums[i]){
                        left = m + 1;
                    }else {
                        // 否则、说明不能覆盖（覆盖后就不符合严格递增了）
                        left = x;
                    }
                }
                // 如果flag=true 覆盖。
                if (left < x){
                    dp[x] = nums[i];
                }
            }else {
                dp[++x] = nums[i];
            }
        }
        return x+1;
    }

==============================================================================

高级算法

4、寻找两个正序数组的中位数【归并排序、二分查找】

此题目的：并不是遍历所有！而是找到某个数 (中位数)
解法一：由于是两个正序数组中寻找：考虑是否使用【归并】化为一个数组？
解法二：寻找【顺序数组中】的某个数？考虑使用二分查找减少查找次数(每次排除一半！)

给定两个大小分别为m和n的正序数组nums1和nums2。请你找出并返回这两个正序数组的中位数、
示例：nums1 = [1,3] nums2 = [2] 输出：2
示例：nums1 = [1,2] nums2 = [3,4] 输出：2.5
我的结论是找规律：nums1求和 = sum1 nums2求和 = sum2 中位数：sum1 + sum2 / 2

显然，我的这种做法虽然能做出来。但是没有用到所谓的归并排序算法，时间O(m + n)。

    public static double getMidNum(int[] nums1, int[] nums2) {
        int m = nums1.length;
        int n = nums2.length;
        double sum1, sum2;
        int midm = m / 2, midn = n / 2;
        if (m == 0) {
            sum1 = 0;
        } else if (m == 1) {
            sum1 = nums1[0];
        } else {
            if (m % 2 == 0) {
                sum1 = (nums1[midm - 1] + nums1[midm]) / 2;
            } else {
                sum1 = nums1[midm] / 2;
            }
        }
        if (n == 0) {
            sum2 = 0;
        } else if (n == 1) {
            sum2 = nums2[0];
        } else {
            if (n % 2 == 0) {
                sum2 = (nums2[midn - 1] + nums2[midn]) / 2;
            } else {
                sum2 = nums2[midn] / 2;
            }
        }
        if (m == 0) {
            return sum2;
        } else if (n == 0) {
            return sum1;
        } else {
            return (sum1 + sum2) / 2;
        }
    }

来看看【归并排序】算法的解题步骤：时间O(m + n) 空间O(m + n)

int[] nums;
    int m = nums1.length;
    int n = nums2.length;
    nums = new int[m + n];
    // 如果nums1为空，则可以直接返回nums2的中位数
    if (m == 0) {
        if (n % 2 == 0) {
            return (nums2[n / 2 - 1] + nums2[n / 2]) / 2.0;
        } else {

            return nums2[n / 2];
        }
    }
    // 如果nums2为空，则可以直接返回nums1的中位数
    if (n == 0) {
        if (m % 2 == 0) {
            return (nums1[m / 2 - 1] + nums1[m / 2]) / 2.0;
        } else {
            return nums1[m / 2];
        }
    }
// 当两个数组都不为空时，通过while循环合并两个数组
    int count = 0;
    int i = 0, j = 0;
    while (count != (m + n)) {
    // 如果nums1的指针走完了，则把nums2剩余的数全部加进来
        if (i == m) {
            while (j != n) {
                nums[count++] = nums2[j++];
            }
            break;
        }
        // 如果nums2的指针走完了，则把nums1剩余的数全部加进来
        if (j == n) {
            while (i != m) {
                nums[count++] = nums1[i++];
            }
            break;
        }
// 把目前两个数组的i j指针对应的值中，较小的值放入归并后的数组中！
        if (nums1[i] < nums2[j]) {
            nums[count++] = nums1[i++];
        } else {
            nums[count++] = nums2[j++];
        }
    }
// 最后输出 合并后的数组的 中位数
    if (count % 2 == 0) {
        return (nums[count / 2 - 1] + nums[count / 2]) / 2.0;
    } else {
        return nums[count / 2];
    }

【二分查找】 时间复杂度达到了极致！：O(log(m+n)) 空间复杂度O(1)
根据中位数的定义：【m+n为奇数】时：中位数为两个数组中【第(m+n)/2 + 1个】元素。
【m+n为偶数】时，中位数为两个数组中【第(m+n)/2个】元素 he 【第(m+n)/2 + 1个】元素的平均值
因此—> 题目转换为：寻找两个有序数组中：第k小的数：与m+n的奇偶性相关

   public double findMedianSortedArrays(int[] nums1, int[] nums2) {
    int n = nums1.length;
    int m = nums2.length;
// 如果n+m是偶数，则中位数为第left和right的平均值
    int left = (n + m + 1) / 2;
    int right = (n + m + 2) / 2;
    //将偶数和奇数的情况合并，如果是奇数，会求两次同样的 k 。
    return (getKth(nums1, 0, n - 1, nums2, 0, m - 1, left) + getKth(nums1, 0, n - 1, nums2, 0, m - 1, right)) * 0.5;  
}
    
    private int getKth(int[] nums1, int start1, int end1, int[] nums2, int start2, int end2, int k) {
// eg: 6 = 5 - 0 + 1;
        int len1 = end1 - start1 + 1;
        int len2 = end2 - start2 + 1;
        //让 len1 的长度小于 len2，这样就能保证如果有数组空了，一定是 len1 ———调整参数顺序
        if (len1 > len2) return getKth(nums2, start2, end2, nums1, start1, end1, k);
        if (len1 == 0) return nums2[start2 + k - 1];
//出口：当k被化为求的是第1小的数，就可以返回了！
        if (k == 1) return Math.min(nums1[start1], nums2[start2]);
// 为防止索引越界：
//如果k/2比数组长度还大，那最多只能取数组长度那么长
// i j 为本次要排除掉的第x个数对应的数组下标
        int i = start1 + Math.min(len1, k / 2) - 1;
        int j = start2 + Math.min(len2, k / 2) - 1;
// 由于是有序递增数组，所以可以直接排除较小的
        if (nums1[i] > nums2[j]) {
            return getKth(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1));
        }
        else {
            return getKth(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1));
        }
    }

---

23、合并K个升序链表【合并2个有序链表（方法二）升级版】

给你一个【链表数组】，每个链表都是升序排序。请你将所有链表合并为一个升序链表，并返回。
eg：lists = [[1,4,5], [1,3,4], [2,6]]。输出：[1,1,2,3,4,4,5,6]
合并K个升序链表——>就是合并2个有序链表（第21题）的升级版
21题用得递归。但这里没有用递归哈。

    private static ListNode result = null;

    public static void main(String[] args) {
        ListNode list1 = new ListNode(1);
        list1.next = new ListNode(4);
        list1.next.next = new ListNode(5);
        ListNode list2 = new ListNode(1);
        list2.next = new ListNode(3);
        list2.next.next = new ListNode(4);
        ListNode list3 = new ListNode(2);
        list3.next = new ListNode(6);
        ListNode[] parm = {list1,list2,list3};
        // 参数组装完毕
        StringBuilder sb = new StringBuilder();
        sb.append("head");
        ListNode listNode = mergeKListNode(parm);
        // 输出结果
        while (listNode != null) {
            sb.append( "->" + listNode.val);
            listNode = listNode.next;
        }
        System.out.println(sb);
    }

    private static ListNode mergeKListNode(ListNode[] lists){
    // 特判
    if (lists.length == 0){
        return null;
    }
    int k = lists.length;
    // 每次取链表数组的两个链表元素来合并为一个新的链表。
    // 合并后的结果链表。又作为参数和下一个链表元素合并
        for (int i = 0; i < k; i++) {
        // head.next为2个链表合并后的第一个节点
            // 赋给result。即：result = head.next; 即result为新链表的头结点。
            // 即：result就代表着新的链表
            result = mergeTwoListNode(result ,lists[i]);
        }
        return result;
    }

    private static ListNode mergeTwoListNode(ListNode list1, ListNode list2){
        if (list1 == null || list2 == null){
            return list1 == null ? list2 : list1;
        }
        // 因为要构造一个新的链表。首先要先创建一个哑元节点head。指向该链表的第一个节点。
        ListNode head = new ListNode(0);
        // 声明一个指针——>使得head.next永远指向这个链表的头结点。
//（复制一个head节点作为指针：这是必要的！如果直接拿head当指针去移动。则最后返回时，head就会在尾巴，找不到链表头了）
        ListNode pointer = head, first = list1, second = list2;
        // 当本轮要比较的节点：list1和List2都不为null时。把小的值加入结果
        while (first != null && second != null){
        if (first.val < second.val){
            // 小的节点添加进结果
            pointer.next = first;
            // 指针后移
            first = first.next;
        }else {
            pointer.next = second;
            second = second.next;
        }
        pointer = pointer.next;
        }
        // 当其中某个链表被拼接完了，则另一个链表直接接上即可
        pointer.next = (first != null ? first : second);
        // head.next为2个链表合并后的首节点（代表该链表）。而head是new出来的一个dummy节点
        return head.next;
    }
    
    static class ListNode{
        private int val;
        private ListNode next;
        public ListNode(int value){
            this.val = value;
        }
    }

---

25、翻转K个一组的链表

给你一个链表：以K个节点为一组，对其进行反转。并返回反转后的链表。
如果节点数不足K，则保持原样
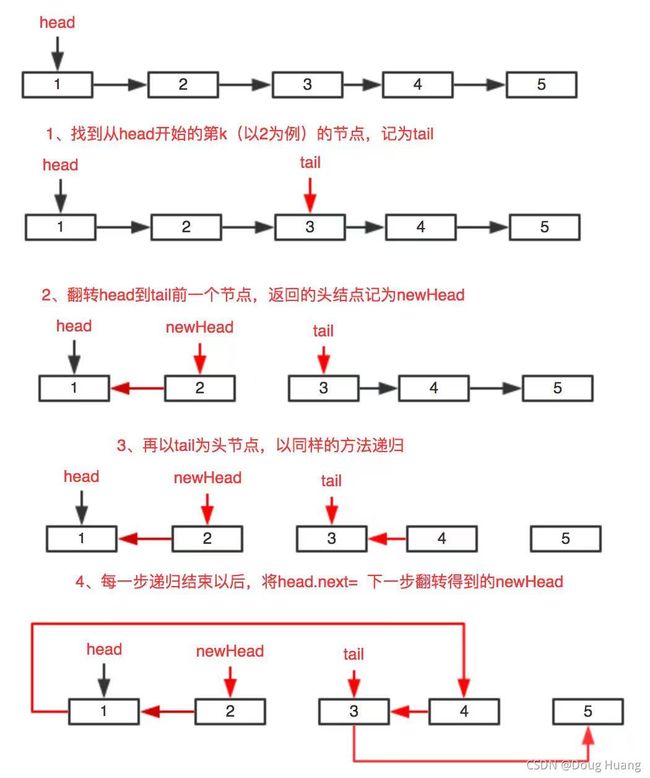
反转链表图解
关键步骤：
1、设一个dummy节点：作为
2、用临时变量暂存下一次要反转的链表头：即 next = head.next;
3、执行反转操作：head.next = pre;

 public static void main(String[] args) {
        ListNode list1 = new ListNode(1);
        list1.next = new ListNode(2);
        list1.next.next = new ListNode(3);
        list1.next.next.next = new ListNode(4);
        list1.next.next.next.next = new ListNode(5);

        StringBuilder sb = new StringBuilder();
        sb.append("head");
        ListNode listNode = reverseKGroup(list1, 3);
        // 输出结果
        while (listNode != null) {
            sb.append( "->" + listNode.val);
            listNode = listNode.next;
        }
        System.out.println(sb);
    }

       public static ListNode reverseKGroup(ListNode head, int k) {
        if (head == null || head.next == null) {
            return head;
        }
        // tail节点就是下一轮要翻转的链表的头结点。
        ListNode tail = head;
        for (int i = 0; i < k; i++) {
            //剩余数量小于k的话，则不需要反转。
            if (tail == null) {
                return head;
            }
            tail = tail.next;
        }
        // 反转前 k 个元素
        ListNode newHead = reverse(head, tail);
        // 本轮翻转结束：递归：让本组的旧头head指向下一组的新头newHead
        //reverseKGroup(tail, k);返回的是：newHead。
        // 即：让head（旧头/新尾）指向newHead
        head.next = reverseKGroup(tail, k);

        return newHead;
    }
    /*
    左闭右开区间
     */
    private static ListNode reverse(ListNode head, ListNode tail) {
        // 前一节点
        ListNode newHead = null;
        ListNode next = null;
        while (head != tail) {
        // 先用temp变量暂存head.next节点（摘下 head的next指针）
            // 拿到头结点的下一个节点：next节点
            next = head.next;
            【关键步骤】
            // 翻转：让head的指针指向newHead (第一轮时newHead=null)
            head.next = newHead;
            // 将本轮head赋给newHead（本轮的head就是新的newHead）
            newHead = head;
            // 将head指针后移一位（head = head.next 当前next设为新的head）
            head = next;
        }
        return newHead;

    }

    static class ListNode{
        private int val;
        private ListNode next;
        public ListNode(int value){
            this.val = value;
        }
    }

---

30、串联所有单词的子串【滑动窗口】

给定一个字符串s，和一些【长度相同】的单词words。
找出s中恰好可以由words中所有单词串联组成的子串的起始位置。
串联成的子串中间不能有其他字符。【不需要考虑单词的串联顺序】
为什么没想出来？：
1、审题：单词的长度是相同的！ 即第一个单词的长度就是后面所有单词的长度。因此单词长度可以作为步长
2、【突破点】：考虑到单词串联顺序的问题、如何解决不同串联顺序下形成不同的子串？
用HashMap集合存储每个单词的个数。用temp临时map存储已经消耗了的单词个数
3、以单词组的总长度来截取子串、以单词的长度len为步长、构建一个滑动窗口、比较子串是否符合条件

    public static void main(String[] args) {
        String[] words = {"bar","foo","the"};
        System.out.println(findSubstring("barfoofoobarthefoobarman", words));
    }
    public static List<Integer> findSubstring(String s, String[] words){
        // allWords存储每个单词的个数
        HashMap<String, Integer> allWords = Maps.newHashMap();
        for (String word : words) {
            allWords.put(word,allWords.getOrDefault(word, 0) + 1);
        }
        // wordNums：单词个数  len：单词长度（步长）
        int wordNums = words.length, len = words[0].length();
        outer:for (int i = 0; i < s.length() - wordNums * len + 1; i += len) {
            // 临时map、存放当前滑动窗口内已经用的单词及所用次数
            HashMap<String, Integer> temp = Maps.newHashMap();
            // 存储本轮结果集
            List<Integer> result = new ArrayList<>();
            // 本轮滑动窗口中的字符串
            String window = s.substring(i, i + wordNums * len);
            // 对该窗口内的字符串进行比较
            for (int j = 0; j < window.length() - 1; j += len) {
                // 取出第一个单词
                String word = window.substring(j, j + len);
                // allWords中包含这个单词，并且temp中还有可用次数
                if (allWords.containsKey(word) && temp.getOrDefault(word,0) < allWords.get(word)){
                    // 使用次数+1
                    temp.put(word, temp.getOrDefault(word,0) + 1);
                    // 单词下标加入结果集
                    result.add(i + j);
                }else {
                    //如果不包含单词、或没有可用次数了。则跳出内层循环、执行下一轮外层循环
                    continue outer;
                }
            }
            // 如果结果集.size == 单词数。则说明找到结果了
            if (result.size() == wordNums){
                return result;
            }
        }
        return null;
    }

---

32、最长的有效括号【栈】

给你一个只包含( )的字符串、找出最长有效且连续的子串，返回其长度
需要找出子串、能联想到需要记录有效字符的索引（记录有效子串的最左索引，和最右索引）
和20题类似，这里也用栈的数据结构。区别是这里的栈中存的是有效符号的下标！
==用到了一个新的API。 stack.peek();——>返回：栈顶元素 ==
maxLen = 最后一个有效 ‘)’ 的索引 - 最前一个有效 ‘(’ 的索引
【始终保持栈底元素为最后一个没有被匹配到的右括号的下标】

    private static int maxEffectiveStr(String s){
        if (s.length() == 0){
            return 0;
        }
        int maxLen = 0;
        // 定义一个栈
        Deque<Integer> stack = new LinkedList<>();
        // 为了解决特殊情况：s = “()”或“(())”等括号完全匹配时：
        //  stack.peek() == null 、计算不出答案
        stack.push(-1);
        // 遍历字符串
        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            if (c == '('){
                stack.push(i);
            }else {
                stack.pop();
                // 【始终保持栈底元素为最后一个没有被匹配到的右括号的下标】
                // 这样就能保证 s = "()))()()"这种)个数> (的情况也能算出答案
                // i - stack.peek() = 7 - 3 = 4 ——> )>(个数时：
                // 栈中只有一个元素：即最后一个没有匹配的 ) 的 下标
                if (stack.isEmpty()){
                    stack.push(i);
                }else {
                    maxLen = Math.max(maxLen, i - stack.peek());
                }
            }
        }
        return maxLen;
    }

---

37、解数独【回溯递归】

36题升级版、这题需要我们解出来。
回溯：相当于撤回的意思、应用于多道选择题、且每个选择题有多个答案可选时、
先假设先选答案A、然后按答案A这条分支递归走下去、如果发现是错的、则撤回到上一轮。
上一轮还是错的、就撤回到上上轮
思路：已经想到了：假设碰到第一个空白格时、可供选择的数字有3 7 9、那么这个空白格该填入哪个呢？
解答：不妨先填入3、然后再往下一个空白格继续填入、如果下个空白格没有数字可以填入（冲突了）
那么就回到上一层（如果回到上一层时发现还是冲突、则回到上上层）、
更改填入的数字为7、如果下一轮还是冲突、就再改为填入9——>因为数独肯定有解、所有总能找到一个出口

    // 用一个List 记录每个空白格的行i和列j
    private static List<int[]> spaces = new ArrayList<>();
    // row col box第一维是 行/列/3X3格号
    // 第二维长度设为10、是为了能存9这个数字： 长度是指从下标0开始的长度
    // 对应行中已出现的数字
    private static int[][] row = new int[9][10];
    // 对应列中已出现的数字
    private static int[][] col = new int[9][10];
    // 对应3x3方格中已出现的数字
    private static int[][] box = new int[9][10];
    // 用作方法出口（终止for循环）
    private static boolean valid = false;

    public static void main(String[] args) {
        char[][] board = new char[9][9];
        char[] param = {'5','3','.',  '.','7','.',  '.','.','.',
                        '6','.','.',  '1','9','5',  '.','.','.',
                        '.','9','8',  '.','.','.',  '.','6','.',
                
                        '8','.','.',  '.','6','.',  '.','.','3',
                        '4','.','.',  '8','.','3',  '.','.','1',
                        '7','.','.',  '.','2','.',  '.','.','6',
                
                        '.','6','.',  '.','.','.',  '2','8','.',
                        '.','.','.',  '4','1','9',  '.','.','5',
                        '.','.','.',  '.','8','.',  '.','7','9'};
        int x = 0;
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                board[i][j] = param[x];
                x++;
            }
        }
        solution4Sudoku(board);
        for (int i = 0; i < 9; i++) {
            StringBuilder sb = new StringBuilder();
            for (int j = 0; j < 9; j++) {
                char c = board[i][j];
                sb.append(c + "  ");
            }
            System.out.println(sb);
        }
    }

    private static void solution4Sudoku(char[][] board) {
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                if (board[i][j] == '.') {
                    spaces.add(new int[]{i,j});
                }else {
                    int target = board[i][j] - '0';
                    row[i][target] = col[j][target] = box[(i/3)*3 + j/3][target] = 1;
                }
            }
        }
        dfs(board, 0);
    }

    private static void dfs(char[][] board, int pos){
        // 【递归出口】：空白格数已经被匹配完了
        if (spaces.size() == pos){
            // 设置valid=true——>找到出口了
            valid = true;
            // return：本次方法执行结束、即返回到上一次递归调用dfs处、
            // 然后进行下一轮for循环、判断 !valid不成立、跳出循环、上次递归dfs方法执行完毕、
            // 继续跳回上一轮、跳到最顶上时、最顶一轮也因valid=true跳出for循环而执行完毕
            return;
        }
        int[] ints = spaces.get(pos);
        int i = ints[0], j = ints[1];
        for (int num = 1; num < 10 && !valid; num++){
            // row col box中记录着对应行列中、已经出现过的数字
            // eg：行列格 中、都未出现的数字有 3 7 9、那么我们先假定当前空白格填入的数字是3、
            // 如果填入3后、递归到的后面的某个空白格也需要填入3（无数字可选、冲突了）
            // 那就要回溯到本轮、清空本轮选择的数字3、然后假定本轮空白格填入7、再次尝试！

            // 判断这个数字是否在行列格中出现过。
            if (row[i][num] == 0 && col[j][num] == 0 && box[(i/3)*3 + j/3][num] == 0){
                // 如果找到了行列格中都未出现的数字（假设找到3 7 9、我们选择填入3试试看能不能走到递归出口）、
                // 则在对应行 列 格中、记录该数字已经被使用。
                row[i][num] = col[j][num] = box[(i/3)*3 + j/3][num] = 1;
                // 将该数字的字符放入数独中
                board[i][j] = (char)(num + '0');
                // 递归开始为下一个空白格寻找合法数字
                // 如果本轮num分配正确（所有空白格都能找到匹配的数字）、那么会在出口处return
                dfs(board, pos + 1);
                // 如果按本轮递归层中选出num分给本轮空白格是错误的：不能使所有空白格都分配到合法的数字
                // 即：（没有走到出口处return）（说明本轮为该空白格假定的数字num会导致其他空白格无数字可选择）
                // 因此：回溯到这一层（即：递归dfs方法时没有return回去、而是执行完了、则会走到下面的代码）
                // 设置本轮选择出的数字3为原始状态（未使用）
                row[i][num] = col[j][num] = box[(i/3)*3 + j/3][num] = 0;
                // 走下一轮for循环、选择数字7再试试
            }
        }
    }