西瓜书入门辅助【机器学习 周志华】一些关于机器学习的重要基础概念提炼

周志华. 机器学习 = Machine Learning. 清华大学出版社, 2016. Print.

第一章：绪论

1. 机器学习所研究的主要内容：关于在计算机上从数据中产生模型model的算法，即学习算法(learning algorithm)

2. 数据集：数据记录的集合；

   示例 instance：每条记录关于的一个事件或对象，一个示例称为一个特征向量

   属性 attribute/特征 feature：事件或对象在某方面的性质或表现

   属性空间 attribute space/样本空间 sample space：属性张成的空间

   分类 classification：预测的是离散值，如好瓜坏瓜。只有两个类别叫二分类。

   回归 regression：预测的是连续值，如瓜的甜度

   聚类 clustering：数据集中的数据划分成若干组，每组称为簇 cluster

   泛化能力 generalization：学得模型适用于新样本的能力

   归纳 induction：特殊到一般的泛化过程，从具体的事实归结出一般性规律

   演绎 deduction：从基础原理推演出具体状况

3. 奥卡姆剃刀 Occam’s razor：若有多个假设与观察一致，则选择最简单的那个。

4. NFL -No free Lunch Theorem：总误差与学习算法无关，即若考虑所有潜在的问题，则所有的学习算法一样好。要谈论算法的相对优劣，必须针对具体的学习问题。

第三章：线性模型

1. 线性模型 linear model：一个通过属性的线性组合来进行预测的函数

   $f(x)=w^T+b$ $w=(w_1;w_2;...;w_d)$

   w，b学得之后，模型得以确定

   线性回归 linear regression：试图学得一个线性模型以尽可能准确地预测实值输出标记。即试图学得

   $f(x_i)=w{x}_i+b$使得$f(x_i)\approx y_i$

   性能度量：均方误差 square loss/欧式距离 Euclidean distance；交叉熵 cross-entropy-loss$L=-[ylog\hat{y}+(1-y)log(1-\hat{y})]$

   最小二乘法 least square method：

   $(w^{\ast },b^{\ast })=ar{g}_{(w,b)}min\sum _{i=1}^m(y_i-w{x}_i-b{)}^2$

   线性回归模型的最小二乘参数估计 parameter estimation：求解w和b使$\sum _{i=1}^m(y_i-w{x}_i-b{)}^2$最小化的过程

2. 对数几率回归 logistic regression：分类学习方法，解决分类任务
   阶跃函数 unit-step function：预测值z大于零判为正例，小于零判为反例，临界值可任意判别。KaTeX parse error: No such environment: equation at position 7: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ y=\left\{ \beg…
   问题：不连续，希望找到一个单调可微的函数替代阶跃函数。若想给一个阈值进行分类，不同的量量纲不通，用logistic 统一量纲，转成[0,1]区间进行分类
   Sigmoid 函数：将z值转化为一个接近0或1的y值，并且输出值在z=0附近变化很陡。

   $y=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-(w^{T}x+b)}}$
   $\Rightarrow$ $p(y=0|x)=\frac{1}{1+e^{-(w^{T}x+b)}}$, $p(y=1|x)=\frac{e^{-(w^{T}x+b)}}{1+e^{-(w^{T}x+b)}}$
   极大似然法 maximum likelihood method：利用已知的样本结果信息，反推最具有可能（最大概率）导致这些羊本结果出现的模型参数值。以此求解w和b。
   对数似然 log-likelihood：
   $l(w,b)=\sum _{i=1}^{m}lnp(y_i|x_i;w,b)$
   令$\beta =(w;b)$，有
   $l(\beta )=\sum _{i=1}^m(-y_i{\beta }^T\widehat{x_i}+ln(1+e^{{\beta }^T\widehat{x_i}}))$
   关于$\beta$的高阶课到连续凸函数，求解可用数值优化算法：梯度下降法 gradient descent method，牛顿法 Newton method

3. 线性判别分析 Linear Discriminant Analysis：给定训练样例集，设法将样例投影到一条直线上，使得同样类别的样例的投影点尽可能接近，异样样例的投影点尽可能远离。
   投影点尽可能接近：同类样例投影点协方差尽可能小；让异类样例的投影点尽可能远离：类中心之间的距离尽可能大。

4. 类别不平衡问题 class-imbalance：分类任务中不同类别的训练样例数目差别很大。
   解决：对多的样例欠采样 undersampling；对少的样例过采样 oversampling；嵌入再缩放决策依据，即阈值移动th reshold-moving

第四章：决策树

1. 决策树 decision tree：基于树结构进行决策。一棵决策树包含一个根节点、若干个内部节点和若干个叶节点，叶节点对应与决策结果，其他每个节点对应于一个属性测试。基本流程遵循分而治之 divide-and-conquer策略
   关键：如何选择最有划分属性。我们希望决策树的分支结点所包含的样本尽可能属于同一类别，即结点纯度purity越来越高
   信息熵 information entropy：度量样本集合纯度的常用指标
   $Ent(D)=-\sum _{k=1}^{|y|}{p}_{k}lo{g}_2{p}_k$
   通过信息熵可计算信息增益 information gain
   决策树过拟合处理办法：
   • 预剪枝 prepruning：对每个节点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分并将当前结点标记为叶节点。
   • 后剪枝 postpruning：先从训练集生成一棵完整的决策树，然后自底向上地对叶结点进行考察，若将该节点对应的子树替换为叶节点能带来决策树泛化性能提升，则将该子树替换为叶节点。

第五章：神经网络

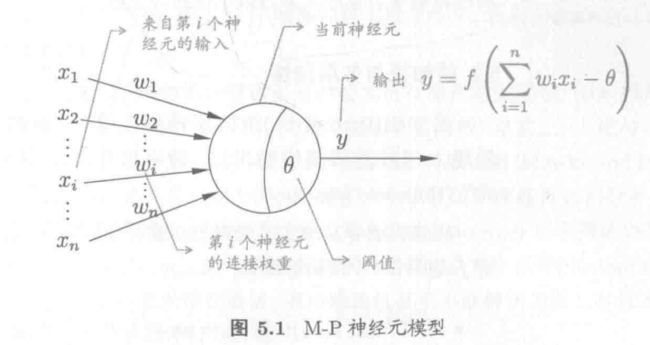
总结：神经网络的学习过程，就是根据训练数据来调整神经元之间的连接权重 connection weight，以及每个功能神经元的阈值。

1. M-P神经元模型：神经元接受到来自n个其他神经元传递过来的输入信号，这些输入信号通过带权重的连接进行传递，神经元收到的总输入值与神经元的阈值进行比较，然后通过激活函数 activation function处理以产生神经元的输出。

   激活函数：Sigmoid 函数能把在较大范围内变化的输入值挤压到（0,1）输出值范围内

2. 感知机Perceptron：两层神经元构成。可解决线性可分问题。

   学习规则：对训练样例(x,y)，若当前感知机输出为$\hat{y}$，则感知机权重这样调整：

   $w_i\leftarrow wi+\Delta w_i$

   $\Delta w_i=\eta (y-\hat{y})x_i$

   $\eta \in (0,1)$称学习率 learning rate 一般设为0.1

3. 多层前馈神经网络 multi-layer feedforward neural networks：多层功能神经元，每层神经元与下一层神经元全互联，神经元之间不存在同层连接，也不存在跨层连接。

4. 误差逆传播算法 error BackPropagation - BP：基于梯度下降法的训练多层网络的算法，可训练多层前馈神经网络。

   BP算法的目标是要最小化训练集D上的累积误差

5. 累积误差逆传播 accumulated error backpropagation：读取整个训练集D一遍后才对参数进行更新

6. 防止过拟合：

   • 早停 early stopping
   • 正则化 regularization：在误差目标函数中增加一个用于描述网络复杂度的部分，如添加连接权与阈值的平方和，训练过程将会偏好比较小的连接权和阈值，使网络输出更加光滑。

7. 跳出局部最小 local minimum：

   • 从多个初始点开始搜索：以多组不同参数初始化多个神经网络，按标准方法训练后取误差小的。
   • 模拟退火 simulated annealing：每一步都以一定的概率接受比当前解更差的结果。
   • 随机梯度下降

8. RBF Radial Basis Function 径向基函数网络：

   • 利用随机采样、聚类等，确定神经元中心$c_i$。
   • 利用BP算法确定参数$w_i$和${\beta }_i$

9. ART Adaptive Resonance Theory 自适应谐振理论网络：缓解可塑性稳定性窘境 stability-plasticity dilemma，可塑性指神经网络学习新知识的能力，稳定性指神经网络在学习新知识时保持对旧只是的记忆。

   竞争型学习 competitive learning：无监督学习，网络的输出神经元互相竞争，每一时刻仅有一个竞争获胜的神经元被激活，即胜者通吃 winner-take-all 原则

10. SOM Self-Organizing Map 自组织映射网络：竞争学习型无监督神经网络，将高维输入数据映射到低维空间，同时保持输入数据在高维空间的拓扑结构，即将高维空间中相似的样本点映射到网络输出层中的邻近神经元。

11. 级联相关 Cascade-Correlation 网络：结构自适应网络将网络结构当做学习的目标之一，希望能在训练过程中找到最符合数据特点的网络结构。

    • 级联：建立层次连接的层级结构。
    • 相关：通过最大化新神经元的输出与网络误差之间的相关性 correlation 来训练相关参数。

12. 递归神经网络 recurrent neural networks：允许网络中出现环形结构，从而让一些神经元的输出反馈回来作为输出入信号。可用于时间序列temporal problem，视频处理。

    • Elman网络：类似于多层前馈神经网络，但隐层神经元的输出被反馈回输入。
    • Boltzmann机：为网络定义一个能量，能量最小化时网络达到理想状态。

13. 深度学习 deep learning ：很深层的神经网络，但是多隐层神经网络难以直接用经典BP算法等进行训练，因为误差在多隐层内逆传播时，往往会发散。

    • 无监督逐层训练 unsupervised layer-wise training：每次训练一层隐结点，训练时将上一层隐结点的输出作为输入，而本层隐结点的输出作为下一层隐结点的输入，这成为预训练 pre-training，预训练结束后，在对整个网络进行微调训练 fine-tuning。

      预训练+微调：将大量参数分组，对每组先找到局部较优的参数设置，再基于局部最优联合起来寻找全局最优。

    • 卷积神经网络 Convolutional Neural Network CNN：复合多个卷积层和采样层对输入信号进行加工，然后在连接层实现与输出目标之间的映射。可用于计算机视觉、图像处理。

      • 卷积层：每个卷积层都包含多个特征映射 feature map，每个特征映射是一个由多个神经元构成的平面，通过一种卷积滤波器提取输入的一种特征。
      • 采样层 pooling：基于局部相关性原理进行亚采样，从而在减少数据量的同时保留有用信息。

第六章：支持向量机 SVM

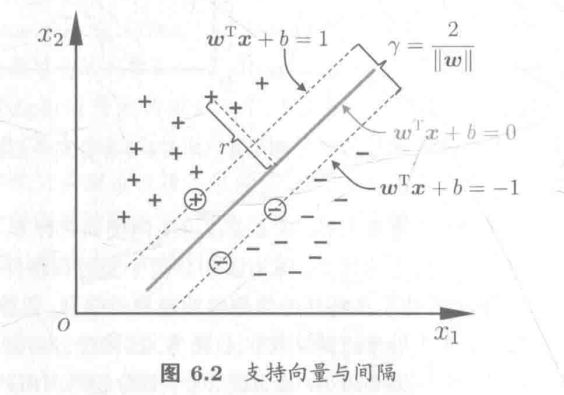
1. 分类学习：基于训练集D在样本空间找到一个划分超平面，将不同类别的样本分开。将样本划分的超平面有很多，我们选择下图粗的那个超平面，因为该划分超平面对训练样本扰动的容忍性最好，对未见示例的泛化能力最强。

   

2. 支持向量 support vector：距离超平面最近的几个训练样本点使$w^T{x}_i+b\ge +1,y_i=+1$ 和 $w^T{x}_i+b\le -1,y_i=-1$ 等号成立，并定义间隔为$\gamma =\frac{2}{||w||}$

支持向量机基本型：找到最大间隔maximum margin，即找到满足$w^T{x}_i+b\ge +1,y_i=+1$ 和 $w^T{x}_i+b\le -1,y_i=-1$ 中约束的参数w和b使间隔$\gamma$最大。
$ma{x}_{w,b}$ $ \frac{2}{||w||}$ $\sim$ $mi{n}_{w,b}$ $\frac{1}{2}||w|{|}^2$

s.t. $y_i(w^T{x}_i+b)\ge 1,i=1,2,...,m$

利用拉格朗日乘子法得到其对偶问题，可使用SMO Sequential Minimal Optimization求解。

3. 核函数 Kernel function：高维向量内积以低维函数内积表示。

   在现实任务中，原始样本空间内也许不存在一个能正确划分两类平面的超平面。因此可尝试将样本从原始空间映射到高维特征空间，使得样本在高维特征空间线性可分。如果原始空间为有限维度，即属性数有限，那么一定存在一个高维特征空间使样本可分。

   令$\varphi (x)$表示x映射后的特征向量，于是划分超平面的模型为$f(x)=w^T\varphi (X)+b$，以此带入支持向量机并求得对偶问题。求解对偶问题时涉及到$\varphi (x_i{)}^T\varphi (x_j)$的计算，这是样本$x_i,x_j$映射到特征空间之后的内积。定义核函数$k(x_i,x_j)=\varphi (x_i{)}^T\varphi (x_j)$

   任何一个核函数都隐式定义了一个再生核希尔伯特空间Reproducing Kernel Hilbert Space, RKHS 的特征空间。特征空间的好坏对支持向量机的性能至关重要，在不知道特征映射的形式时，我们并不知道什么样的核函数是合适的，而核函数也只是隐式定义了这个特征空间。于是，核函数选择称为支持向量机的最大变数。

   

   问题：即使恰好找到了某个核函数使训练集在特征空间中线性可分，也很难断定这个结果不是由过拟合所造成的。

4. 软间隔 soft margin：允许支持向量机在一些样本上出错。改写优化目标，引入损失函数(0/1损失,hinge损失,指数损失，对率损失等)

   $mi{n}_{w,b}$ $\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{l}_{0/1}(y_i(w^T{x}_i+b)-1)$

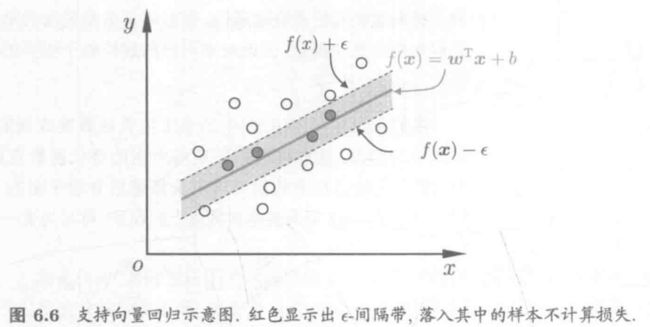
5. 支持向量回归 Support Vector Regression, SVR：假设能容忍$f(x)$与y之间最多有$ϵ$的偏差，相当于以$f(x)$为中心，构建了一个宽度为$2ϵ$的间隔带，若训练样本落入此间隔带则被预测为正确的。

   即SVR问题：$mi{n}_{w,b}$ $\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{l}_{ϵ}(f(x_i)-y_i)$，其中$l_{ϵ}$是$ϵ-$不敏感损失

第七章：贝叶斯分类器

1. 贝叶斯决策论 Bayesian decision theory：在概率框架下实施决策的基本方法。对于分类任务，在所有相关概率都已知的理想情形下，贝叶斯决策论考虑如何基于这些概率和误判损失来选择最优的类别标记。

   条件风险 conditional risk：基于后验概率$P(c_i|x)$获得将样本x分类为$c_i$所产生的期望损失expected loss。

   $R(c_i|x)=\sum _{j=1}^N{\lambda }_{ij}P(c_j|x)$

   任务是寻找一个判定准则以最小化总体风险：$R(h)=E_x[R(h(x)|x)]$

   贝叶斯判定准则 Bayes decision rule：为最小化总体风险，只需在每个样本上选择那个能使条件风险$R(c|x)$最小的类别标记。

   $h^{\ast }(x)=argminR(c|x)$

   此时$h^{\ast }$被称为贝叶斯最优分类器 Bayes optimal classifier

   如何获得后验概率

   • 判别式模型 discriminative models：给定x，直接建模$P(c|x)$来预测c
   • 生成式模型 generative models：先对联合概率分布$P(x,c)$建模，再由此获$P(c|x)$

   条件概率 class-conditional probability：$P(c|x)=\frac{P(x,c)}{P(x)}$或称为似然 likelihood

   贝叶斯定理：$P(c|x)=\frac{P(c)P(x|c)}{P(x)}$

2. 极大似然估计 Maximum Likelihood Estimation, MLE：根据数据采样来估计概率分布参数的经典方法。

   估计类条件概率的一般策略：假定其具有某种特定的概率分布形式，再基于训练样本对概率分布的参数进行估计。概率模型的训练过程就是参数估计 parameter estimation，我们的任务就是利用训练集D估计参数${\theta }_c$。

   参数${\theta }_c$对于数据集$D_c$的似然：$P(D_c|{\theta }_c)=\prod _{x\in D_c}P(x|{\theta }_c)$，连乘容易造成下溢，使用对数似然$LL({\theta }_c)=logP(D_c|{\theta }_c)=\sum _{x\in D_c}logP(x|{\theta }_c)$。对${\theta }_c$进行极大似然估计，就是去寻找最大化似然的参数值$\widehat{{\theta }_c}$

3. 朴素贝叶斯分类器 naïve Bayes classifier：采用属性条件独立性假设 attribute conditional independence assumption，假设每个属性独立地对分类结果发生影响。其分类过程就是基于训练集D来估计类先验概率$P(c)$，并为每个属性估计条件概率$P(x_i|c)$。

4. 半朴素贝叶斯分类器 semi-naïve Bayes classifiers：利用独依赖估计 One-Dependent Estimator，ODE。适当考虑一部分属性之间的相互依赖信息，从而既不需要进行完全联合概率计算，又不至于彻底忽略了比较强的属性依赖关系。

5. 隐变量 latent variable：未观测变量称为隐变量。

   EM Expectation-Maximization 算法：迭代法估计参数隐变量。E——以当前参数推断隐变量分布，并对对数似然求期望；M——寻找参数最大化期望似然。

第八章：集成学习

1. 集成学习 ensemble learning：通过构建并结合多个学习器来完成学习任务。

继承学习的结果通过投票法voting 产生，即少数服从多数。要获得好的集成，个体学习器应好而不同，即学习器不能太坏并且要有多样性。假设基学习器的误差相互独立，则随着集成中个体分类器树木的增大，集成的错误率将指数级下降最终趋向于零。但是现实任务中，个体学习器是为了解决同一个问题训练出来的，他们显然不可能相互独立。因此个体学习器的准确性和多样性存在冲突。集成学习研究的核心就是如何产生好而不同的个体学习器。

集成学习方法：

• Boosting：将弱学习器提升为强学习器的算法，调整每一次训练的样本分布，使后续基学习器对之前基学习器做错的训练样本产生更多关注。个体学习器之间存在强依赖关系、必须串行生成的序列化方法。
• Bagging，随机森林 Random Forest, RF：个体学习器之间不存在强依赖关系、可同时生成的并行化方法。Bagging通过自助采样法 bootstrap sampling，在总数据集中取出一部分样本，再放入总数据集中，因此这些数据在下一次采样时仍有可能被选中。随机森林在以决策树为基学习器构建Bagging集成的基础上，进一步在决策树的训练过程中引入随机属性选择。因此随机森林的多样性不仅来自样本扰动，还来自属性扰动。

2. 基学习器结合策略：

   • 平均法
     • 简单平均 simple averaging
     • 加权平均weighted averaging
   • 投票法
     • 绝对多数投票法 majority voting：得票超过半数
     • 相对多数投票法 plurality voting：得票最多
     • 加权投票法 weighted voting
   • 学习法：Stacking先从初始数据集训练出初级学习期，然后生成一个新数据集用于训练次级学习器。
   • 多样性
     • 误差-分歧分解 error-ambiguity decomposition：个体学习器准确性越高，多样性越大，则集成越好。
     • 多样性度量
       • 不合度量 disagreement measure
       • 相关系数 correlation coefficient
       • Q-统计量 Q-statistic
       • k-统计量 k-statistic
     • 多样性增强
       • 数据样本扰动
       • 输入属性扰动：输入子空间算法 random subspace 从初始属性集中抽取若干属性子集
       • 输出表示扰动：翻转法 Flipping Output 随机改变一些训练样本的标记
       • 算法参数扰动：负相关法 Negative Correlation显式地通过正则化项来强制个体神经网络使用不同参数

第九章：聚类

1. 无监督学习 unsupervised learning：训练样本的标记信息是未知的，目标是通过无标记训练样本的学习来揭示数据的内在性质及规律，为进一步的数据分析提供基础。

   聚类 clustering：将数据集中的样本划分为若干个通常是不相交的子集，每个自己成为一个簇 cluster。聚类过程仅能机动生成簇结构，簇所对应的感念语义仍需由使用者来把握和命名。聚类既能作为一个单独过程，用于寻找数据内在的分布结构，也可作为分类等其他学习任务的前驱过程。

2. 性能度量：我们希望聚类结果簇内相似度 intra-cluster similarity高而簇间相似度 inter-cluster similarity低

   • 外部指标 external index：将聚类结果与某个参考模型 reference model比较
     • Jaccard系数 Jaccard Coefficient, JC
     • FM指数 Fowlkes and Mallows Index, FMI
     • Rand指数 Rand Index, RI
   • 内部指标 internal index：直接考察聚类结果而不利用任何参考模型
     • DB指数 Davies-Bouldin Index, DBI
     • Dunn指数 Dunn Index, DI

3. 距离计算

   • 闵可夫斯基距离 Minkowski distance，即p-范数
   • 欧氏距离
   • 曼哈顿距离 1-范数

4. 原型聚类 prototype-based clustering：假设聚类结构能通过一组原型刻画。算法先对原型进行初始化，然后对原型进行迭代更新求解。

   • k均值算法：针对聚类所得簇划分$C=[C_1,C_2,...,C_k]$最小化平方误差，$E=\sum _{i=1}^k\sum _{x\in C_i}||x-{\mu }_i|{|}_2^2$，采用贪心策略，迭代优化求解此式。K均值算法刻画了簇内样本围绕簇均值向量的紧密程度，E值越小则簇内样本相似度越高。
   • 学习向量量化 Learning Vector Quantization，LVQ：试图找到一组原型向量刻画聚类结构，但是LVQ假设数据样本带有类别标记，学习过程利用样本的这些监督信息来辅助聚类。
   • 高斯混合聚类 Mixture of Gaussian：采用概率模型表达聚类原型，簇划分由原型对应后验概率决定。
   • 密度聚类 density-based clustering：假设聚类结构能通过样本分布的紧密程度确定。从样本密度的角度来考察样本之间的可连接性，并基于可连接样本不断扩展聚类簇以获得最终的聚类结果。DBSCAN算法
   • 层次聚类 hierarchical clustering：在不同层次对数据集进行划分，形成树形聚类结构。AGNES算法将数据集中地每个样本看作一个初始聚类簇，然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并。

第十章：降维与度量学习

1. k近邻学习 k-nearest Neighbor, kNN: 给定测试样本，基于某种距离量度找出训练集中与其最靠近的k个训练样本，然后基于这k个邻居的信息进行预测。最近邻分类器(1NN)虽然简单，但是他的泛化错误率不超过贝叶斯最优分类器的错误率的两倍。

   密采样 dense sample：任一测试样本x附近任意小的$\sigma$距离范围内总能找到一个训练样本，即训练样本的采样密度足够大。

   问题：现实应用中属性维度巨大，不一定能满足密采样条件。在高维情形下出现数据样本稀疏、距离计算困难的问题——维数灾难 curse of dimensionality

2. 降维 dimension reduction：通过某种数学变换将原始高维属性空间转变为一个低维子空间，在子空间中样本密度大幅度提高。因为在很多时候，人们观测到的数据样本虽然是高维的，但与学习任务相关的也许仅仅是某个低维分布，即只是高维空间中的一个低维嵌入 embedding。原始高维空间中的样本点，在这个低维嵌入子空间中更容易学习。

   

   • 多维缩放 Multiple Dimensional Scaling, MDS：要求原始空间中样本之间的距离在低维空间中得到保持
   • 线性降维方法：通过线性变换$Z=W^{T}X$来进行降维

3. 超平面：对于正交属性空间中的样本点，如何用一个超平面对所有样本进行恰当地表达？

   • 最近重构性：样本点到这个超平面的距离足够近
   • 最大可分性：样本点在这个超平面上的投影能尽可能分得开

   主成分分析 Principle Component Analysis, PCA：常用的降维方法

   • 从最近重构性推导：应最小化原样本点与基于投影重构的样本点之间的距离
   • 从最大可分性推导：使投影后样本点的方差最大化

   PCA仅需保留标准正交基向量与样本的均值向量即可通过简单地向量减法和矩阵向量乘法将新样本投影至低维空间中。在低维空间中最小的特征值对应的特征向量被抛弃了，这是降维导致的信息丢失，但这是必要的。舍弃这部分数据之后能使样本的采样密度增大，同时当数据受到噪声影响，最小特征值所对应的特征向量往往与噪声有关。

4. 核化线性降维：线性降维方法有可能丢失原本的低维结构。核化线性降维基于核技巧对线性降维方法进行核化以此进行非线性降维。

   • 核主成分分析 Kernelized PCA, KPCA：引入核函数，通过核函数将样本映射到高维特征空间，再在特征空间中实施PCA

5. 流形学习 manifold learning：拓扑流形概念的降维方法。若低维流形嵌入到高维空间中，则数据样本在高维空间的分布虽然看上去非常复杂，但在局部上仍具有欧式空间的性质。因此可以很容易地在局部建立降维映射关系，然后再设法将局部映射关系推广到全局。

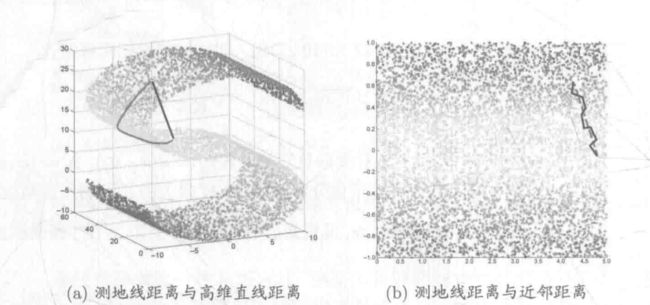
   • 测地线 geodesic距离：两点之间的本真距离

   • 等度量映射 Isometric Mapping, Isomap：保持近邻样本之间的距离。计算两点之间测地线距离的问题，转变为计算近邻连接图上两点之间的最短路径问题。（摸点前进）

   

   • 局部线性嵌入 Locally Linear Embedding, LLE：保持邻域内样本之间的线性关系，即保持$x_i=w_{ij}{x}_j+w_{ij}{x}_k+w_{il}{x}_l$

6. 度量学习 metric learning：对高维数据进行降维的主要目的是希望找到一个合适的低维空间，在此空间中进行学习能比原始空间性能更好。事实上，每个空间对应了在样本属性上定义的一个距离度量，而寻找合适的空间，实质上就是寻找一个合适的距离度量。度量学习的动机是尝试学习出一个合适的距离度量。

第十一章：特征选择与稀疏学习

1. 特征选择 feature selection：从给定特征集合中选择出相关特征子集的过程，是一个重要的数据预处理过程 data preprocessing。在机器学习任务中，获得数据之后通常先进行特征选择，然后再训练学习器。

   特征选择的原因：

   • 维数灾难问题：属性过多，与降维相似的动机，如果能选择出重要特征，仅在一部分特征上构建模型，则维数灾难问题将大为减轻。
   • 去除不相关特征将降低学习任务的难度

   冗余特征 redundant feature：所包含的信息能从其他特征中推演出来。长宽与面积。

   特征选择过程：想要从初始特征集合中选取一个包含了所有重要信息的特征子集，先产生一个候选子集，基于评价结果产生下一个候选子集。

   • 子集搜索 subset search：
     • 前向搜索：从单特征子集开始由少到多逐渐增加相关特征。
     • 后向搜索：从完整特征集合开始，每次尝试去掉一个无关特征。
   • 子集评价 subset evaluation：计算子集的信息熵与信息增益，信息增益越大，特征子集包含的有助于分类的信息越多。

2. 过滤式选择 ：先对数据集进行特征选择，然后再训练学习期，特征选择的过程与后续学习器无关。相当于先用特征选择过程对初始特征进行过滤，再用过滤后的特征来训练模型。

3. 包裹式选择：直接把最终将要使用的学习器的性能作为特征子集的评价准则。即包裹式选择的目的就是为了给学习器选择最有利于其性能、量身定做的特征子集。

4. 嵌入式选择：在过滤式和包裹式特征选择方法中，特征选择过程与学习器训练过程有明显的分别；嵌入式特征选择将特征选择与学习器训练过程融为一体，在同一个优化过程中完成，即在学习器训练过程中自动进行了特征选择。

5. 稀疏表示sparse representation：

   • 设数据集D每行对应一个样本，每列对应于一个特征。矩阵中许多列与当前学习任务无关，通过特征选择去除这些列，则学习器训练过程仅需在较小的矩阵上进行。
   • D所对应矩阵中存在很多零元素，但不是以整行整列形式出现。

6. 字典学习 dictionary learning：学习出一个字典，为普通稠密表达的样本找到合适的字典，将样本转化为合适的稀疏表示形式。

7. 压缩感知 compressed sensing：利用信号本身的稀疏性，从部分观测样本中恢复原信号。

   奈奎斯特采样定理：采样频率达到模拟信号的最高频率的两倍，则采样后的数字信号就保留了模拟信号的全部信息。

第十三章：半监督学习

1. 主动学习 active learning：用标签的数据集训练一个模型，拿这个模型去预测未带标签的数据，把新获得的有标记样本加入标签数据集重新训练模型。

2. 半监督学习 semi-supervised learning：学习器不依靠外界交互，自动地利用未标记样本来提升学习性能。

   未标记样本虽然没有包含直接的标记信息，但若果他们与有标记样本是从同样的数据源独立同分布采样而来，则他们所包含的关于数据分布的信息对建立模型将大有裨益。

3. 利用未标记样本的假设：

   • 聚类假设 cluster assumption：假设数据存在簇结构，同一个簇的样本属于同一个类别。
   • 流形假设 manifold assumption：假设数据分布在一个流形结构上，临近的样本拥有相似的输出值。

4. 生成式方法 generative methods：假设所有数据无论是否有标记都是有由同一个潜在的模型生成的。因此，我们能通过潜在模型的参数将未标记数据与学习目标联系起来，而未标记数据的标记可看做模型的缺失参数，可基于EM算法进行极大似然估计求解。

5. 半监督支持向量机 Semi-Supervised Support Vector Machine, S3VM：试图找到能将两类有标记样本分开，且穿过数据低密度区域的划分超平面。

   • TSVM Transductive Support Vector Machine：先利用labeled学得一个SVM，然后利用这个SVM对unlabeled进行标记指派 label assignemnt，即将SVM预测的结果作为伪标记 pseudo-label赋予unlabeled，此时得到一个标准SVM问题，鱼时刻求解出新的划分超平面和松弛向量。接下来，TSVM找出两个标记指派为异类且很可能发生错误的未标记样本，交换他们的标记，在重新求解更新后的划分超平面。直到有标记数据与无标记数据的平衡参数趋于一致。

6. 半监督聚类 semi-supervised clustering：聚类是典型的无监督学习任务，但是在现实聚类任务中我们往往能够获得一些额外的监督信息。

   • 监督信息
     • 必连 must-link与勿连 cannot-link：前者指样本必属于同一个簇；后者指样本必不属于同一个簇。——约束k均值算法
     • 少量的有标记样本——约束种子k均值算法

第十六章：强化学习

1. 强化学习 reinforcement learning：多次种瓜，在种瓜过程中不断摸索，然后才能总结出更好的种瓜策略。（反思）

马尔科夫决策过程 Markov Decision Process, MDP：机器处于环境E中，状态空间为X，其中每个状态$x\in X$是机器感知到的环境的描述。

机器与环境的关系：在环境中状态的转移、奖赏的返回是不受机器控制的，机器只能通过选择要执行的动作来影响环境，也只能通过观察转移后的状态和返回的奖赏来感知环境。机器要做的是通过在环境中不断地尝试而学得一个策略 policy。策略的优劣取决于长期执行这一策略后得到的累计奖赏。强化学习的目的是找到能使长期积累奖赏最大化的策略。

2. 最大化单步奖赏：

   • 须知道每个动作带来的奖赏
   • 要执行奖赏最大的动作

   问题：一个动作的奖赏是来自于一个概率分布，仅通过一次尝试并不能获得平均奖赏值。

3. K-摇臂赌博机 K-armed bandit：

   • 为得到每个摇臂的期望奖赏——仅探索 exploration-only法：将所有的尝试机会平均分配给每个要摇臂（轮流按下），最后每个摇臂各自的平均吐币概率作为其奖赏期望的期望估计。
   • 为执行奖赏最大的动作——仅利用 exploitation-only法：按下目前最优的（平均奖赏最大的）

   探索-利用困境 Exploration-Exploitation dilemma：探索与利用两者矛盾。想要累计奖赏最大，必须在探索与利用之间达成较好的折中。

   $ϵ$-贪心：基于一个概率对探索和利用进行折中，每次尝试时，以$ϵ$的概率进行探索，即以均匀概率随机选取一个摇臂。以$1-ϵ$的概率进行利用，即选择当前平均奖赏最高的摇臂。

4. 策略评估：在模型已知时，对任意策略$\pi$能估计出该策略带来的期望累积奖赏。利用状态值函数 state value function。

   策略改进：对某个策略的累积奖赏进行评估后，希望对其进行改进。了理想的策略应该能最大化累积奖赏。

5. 蒙特卡罗强化学习：多次采样，然后求取平均累积奖赏来作为期望累积奖赏的近似

6. 直接模仿学习 imitation learning：直接模仿人类专家，对专家决策轨迹数据进行分类或回归算法学得策略模型。学得的这个策略模型可作为机器进行强化学习的初始策略，再通过强化学习方法基于环境反馈进行改进，从而获得更好的策略。

7. 逆强化学习 inverse reinforcement learning：从人类专家提供的范例数据中反推出奖赏函数。