机器学习入门课程学习笔记(斯坦福吴恩达)(上篇)
文章目录
- 一、简介
-
- 1.1 什么机器学习
- 1.2 监督学习(Supervised Learning)
- 1.3 非监督学习(Unsupervised Learning)
- 二、 模型和代价函数(Model and Cost Function)
-
- 2.1 模型描述(Model Representation)
- 2.2 代价函数(Cost Function)
- 2.3 梯度下降(Gradient Descent)
- 三、线性代数
-
- 3.1 矩阵和向量
- 3.2 矩阵的加法和标量乘法(Addition and Scalar Multiplication)
- 3.2 矩阵与向量相乘(Matrix-vector Multiplication)
- 3.3 矩阵与矩阵相乘(Matrix-matrix Multiplication)
- 3.4 矩阵乘法的性质(Matrix Multiplication Properties)
- 3.5 矩阵的逆和转置(Inverse and Transpose)
- 四、多元线性回归(Multivariate Linear Regression)
-
- 4.1 多个特征(Multiple features)
- 4.2 多元线性回归中的梯度下降
- 4.3 梯度下降实战-特征缩放(Feature Scaling)
- 4.4 梯度下降实战-学习率(Learning Rate)
- 4.5 特征和多项式回归(Features and Polynomial Regression)
- 4.6 正规方程(Normal Equation)
- 4.7 正规方程不可逆(Normal Equation Noninvertibility)
- 五、Octave教程
- 六、逻辑回归
-
- 6.1 分类问题(Classification)
- 6.2 Hypothesis Representation
- 6.3 决策边界(Decision Boundary)
- 6.4 逻辑回归的代价函数
- 6.5 简化代价函数和梯度下降(Simplified Cost Function and Gradient Descent )
- 6.6 高级优化(Advanced Optimization)
- 6.7 多分类问题:一对多(Multiclass Classification: One-vs-all)
- 七、解决过拟合问题
-
- 7.1 过拟合问题
-
- 理解高偏差和高方差
- 7.2 包含正则化的代价函数
- 7.3 正则化的线性回归(Regularized Linear Regression)
- 7.4 正则化的逻辑回归(Regularized Logistic Regression)
- 八、神经网络(Neural Networks)
-
- 8.1 非线性假设(Non-linear Hypotheses)
- 8.2 神经和大脑(Neurons and the Brain)
- 8.3 模型表示(Model Representation)
- 8.4 样例1(Examples and Intuitions)
- 8.5 多分类问题(Multiclass Classification)
- 九、神经网络(二)
-
- 9.1 代价函数
- 9.2 反向传播算法(Backpropagation Algorithm)
- 9.5 梯度检测
- 9.6 随机初始化
- 9.7 神经网路总结
一、简介
1.1 什么机器学习
机器学习的定义:一个计算机程序可从经验E(Experience)中学习如何完成任务T(Task),并且随着经验E的增加,性能指标P (performance measure)会不断提高
机器学习的分类:
- 监督学习(Supervised Learning):给定一个数据集,该数据集包含输出结果(标签),程序通过学习,来给输入数据打标签。例如:喂给程序n张动物图片,并且告知它每张图片是什么动物,程序经过学习后,喂给程序一张未打标签的图片,让程序判断这是什么动物
- 非监督学习(Unsupervised Learning):与监督学习正好相反。给定一个数据集,但不给出每个数据集的输出,让程序自己去给数据集进行分类。例如:给定一组基因数据,根据给定的变量(如寿命,地理位置等),自动将其进行分组。
1.2 监督学习(Supervised Learning)
给定一个数据集,该数据集包含输出结果(标签),程序通过学习,来给输入数据打标签。例如:喂给程序n张动物图片,并且告知它每张图片是什么动物,程序经过学习后,喂给程序一张未打标签的图片,让程序判断这是什么动物
监督学习问题的分类:
- 分类问题(Classification Problem):预测的结果是离散值。例如:要预测一张动物照片属于猫、狗或其它等。
- 回归问题(Regression Problem):预测的结果是连续值。例如:预测房屋的价格,结果可以是10000,10001, …
1.3 非监督学习(Unsupervised Learning)
给定一个数据集,但是并不会告诉机器“每个数据集是什么”,然后让机器自己去对这个数据集进行分类。比如给定一组衣服尺寸数据,通过机器学习,将衣服分成“大”、“中”、“小”三类,训练好模型后,再给定一个衣服尺寸数据,机器就可以识别出这是大号还是中号或小号。
二、 模型和代价函数(Model and Cost Function)
2.1 模型描述(Model Representation)
- m m m :训练数据集的样本数量
- x ( i ) x^{(i)} x(i):第 i i i 个样本的输入(特征)
- y ( i ) y^{(i)} y(i): 第 i i i 个样本的输出(目标值)
- ( x ( i ) , y ( i ) ) (x^{(i)}, y^{(i)}) (x(i),y(i)):第 i i i 个样本
- θ 0 , θ 1 , θ 2 , … \theta_0,\theta_1,\theta_2,\dots θ0,θ1,θ2,… :要训练的参数
- h θ ( x ) h_\theta(x) hθ(x) 或 h ( x ) h(x) h(x):训练出的模型(函数)
2.2 代价函数(Cost Function)
代价函数是用来描述“当前模型预测的精确程度”,一般来说,代价函数的值越大,预测的值越不精准,所以,我们优化模型的其中一个目标就是使代价函数尽可能的小
代价函数表示方法不唯一,通常使用以下表示方法:
J ( θ ) = 1 2 m ∑ i = 1 m ( y ^ i − y i ) 2 = 1 2 m ∑ i = 1 m ( h θ ( x i ) − y i ) 2 J(\theta) = \frac{1}{2m} \sum_{i=1}^{m}(\hat{y}_i-y_i)^2 = \frac{1}{2m} \sum_{i=1}^{m}(h_\theta(x_i)-y_i)^2 J(θ)=2m1i=1∑m(y^i−yi)2=2m1i=1∑m(hθ(xi)−yi)2
公式解释:
- J ( θ ) J(\theta) J(θ):代价函数,其中 θ \theta θ 为当前的模型参数。目标就是不断优化参数 θ \theta θ 来使代价函数的值变小
- ( y ^ i − y i ) 2 (\hat{y}_i-y_i)^2 (y^i−yi)2: y ^ \hat{y} y^ 为预测的值, y y y 为实际值。使用预测的值减去实际值,来求得误差值。加平方有两个原因:①消除负号 ②方便求导(如果使用绝对值会不方便求导)
- 1 2 m \frac{1}{2m} 2m1 : 除以 m m m 是为了求平均。除以2为了方便求导,因为求导后,2次方会正好把这个2消掉
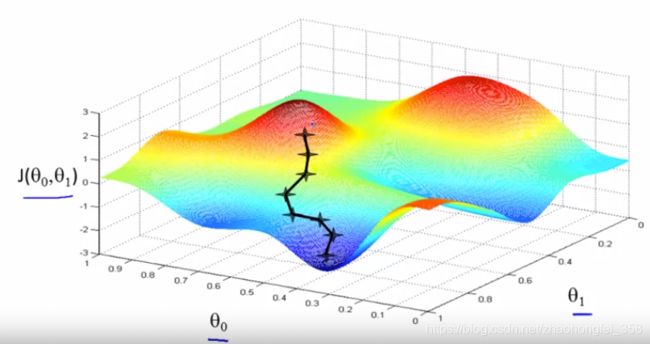
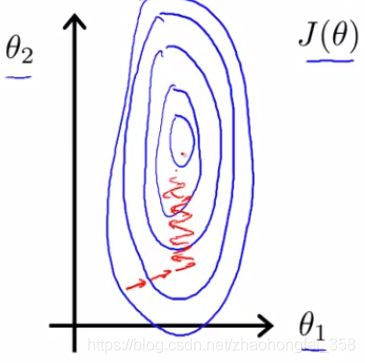
2.3 梯度下降(Gradient Descent)
梯度下降是用来找出当 θ \theta θ 取何值时, J ( θ ) J(\theta) J(θ) 取“最小值” 。
核心思想:对 J ( θ ) J(\theta) J(θ) 进行求导,算出当前 J ( θ ) J(\theta) J(θ)的方向, 然后向着 J ( θ ) J(\theta) J(θ)减小的方向移动 θ \theta θ,直到 θ \theta θ 趋于0
梯度下降算法伪代码:
r e p e a t u n t i l c o n v e r g e n c e { θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) ( f o r j = 0 a n d j = 1 ) } \begin{aligned} &repeat~~until ~~convergence ~~\{ \\ &~~~~~~~~ \theta_j ~:=~ \theta_j - \alpha\frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1) ~~~~(for~~ j=0 ~ and ~ j=1)\\ &\} \end{aligned} repeat until convergence { θj := θj−α∂θj∂J(θ0,θ1) (for j=0 and j=1)}
解释:
:=:赋值操作。在其他语言中,一般使用=,而非:=- repeat until convergence:重复直到收敛为止。不断重复括号里的操作,直到 θ j \theta_j θj 收敛于某一值,也就是 J ( θ 0 , θ 1 ) J(\theta_0, \theta_1) J(θ0,θ1) 趋近于0
- θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) \theta_j ~:=~ \theta_j - \alpha\frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1) θj := θj−α∂θj∂J(θ0,θ1) : α \alpha α为一指定常数,称为学习率(learning rate)。每次 θ j \theta_j θj 向 J ( θ 0 , θ 1 ) J(\theta_0, \theta_1) J(θ0,θ1) 减小的方向移动一点
- ( f o r j = 0 a n d j = 1 ) (for~~ j=0 ~ and ~ j=1) (for j=0 and j=1) : j j j 为 θ \theta θ 的下标,在该例中,有两个需要学习的参数,所以需要对 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 都做上面这个操作
C o r r e c t : S i m u l t a n e o u s u p d a t e t e m p 0 = θ 0 − α ∂ ∂ θ 0 J ( θ 0 , θ 1 ) t e m p 1 = θ 1 − α ∂ ∂ θ 1 J ( θ 0 , θ 1 ) θ 0 : = t e m p 0 θ 1 : = t e m p 1 \begin{aligned} &Correct: Simultaneous~ update \\ & temp0 = \theta_0 - \alpha\frac{\partial}{\partial \theta_0} J(\theta_0, \theta_1) \\ & temp1 = \theta_1 - \alpha\frac{\partial}{\partial \theta_1} J(\theta_0, \theta_1) \\ & \theta_0 := temp0 \\ & \theta_1 := temp1 \\ \end{aligned} Correct:Simultaneous updatetemp0=θ0−α∂θ0∂J(θ0,θ1)temp1=θ1−α∂θ1∂J(θ0,θ1)θ0:=temp0θ1:=temp1
需要注意: θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 要同时更新,他们都更新后才能进入下一轮循环。
学习率 α \alpha α:学习率决定每次移动的步长
三、线性代数
3.1 矩阵和向量
矩阵(Matrix):矩形的一组数字类型的数组,一般用大写字母表示。例如:
A = [ 123 444 454 1238 4264 1128 ] A=\begin{bmatrix} 123 & 444 \\ 454 & 1238 \\ 4264 & 1128 \\ \end{bmatrix} A=⎣⎡123454426444412381128⎦⎤
矩阵的维度(Dimension of matrix):矩阵是一个二维数组,维度用 行 数 × 列 数 行数\times 列数 行数×列数 表示。例如,上面这个矩阵维度为 3 × 2 3\times 2 3×2,记作 R 3 × 2 \reals^{3\times 2} R3×2
矩阵的元素(Matrix Elements ( entries of matrix )): A i j A_{ij} Aij 表示矩阵 A A A 中的第 i i i 行 第 j j j 列的元素。例如, A 11 = 123 A_{11}=123 A11=123 , A 32 = 1128 A_{32}=1128 A32=1128
向量(Vector):一个 n × 1 n\times 1 n×1 的矩阵就是一个向量,一般用小写字母表示。例如:
y = [ 213 54 314 ] y = \begin{bmatrix} 213 \\ 54 \\ 314 \\ \end{bmatrix} y=⎣⎡21354314⎦⎤
向量的元素: y i y_i yi 表示向量的第 i i i 个元素。例如 y 2 = 54 y_2=54 y2=54
3.2 矩阵的加法和标量乘法(Addition and Scalar Multiplication)
矩阵的加法(Matrix Addition):两个矩阵相加得到一个新的矩阵。做法为对应元素相加,要求两个矩阵维度必须一样,要不然没法对应元素相加。例如:
[ 1 0 2 5 3 1 ] + [ 4 0.5 2 5 0 1 ] = [ 5 0.5 4 10 3 2 ] \begin{bmatrix} 1 & 0 \\ 2 & 5 \\ 3 & 1 \\ \end{bmatrix} + \begin{bmatrix} 4 & 0.5 \\ 2 & 5 \\ 0 & 1 \\ \end{bmatrix} = \begin{bmatrix} 5 & 0.5 \\ 4 & 10 \\ 3 & 2 \\ \end{bmatrix} ⎣⎡123051⎦⎤+⎣⎡4200.551⎦⎤=⎣⎡5430.5102⎦⎤
标量乘法(Scalar Multiplication): 矩阵乘以一个数得到一个新的矩阵,做法为每个元素都乘以该数。例如:
3 × [ 1 0 2 5 3 1 ] = [ 3 0 6 15 9 3 ] 3 \times \begin{bmatrix} 1 & 0 \\ 2 & 5 \\ 3 & 1 \\ \end{bmatrix} = \begin{bmatrix} 3 & 0 \\ 6 & 15 \\ 9 & 3\\ \end{bmatrix} 3×⎣⎡123051⎦⎤=⎣⎡3690153⎦⎤
3.2 矩阵与向量相乘(Matrix-vector Multiplication)
矩阵与向量相乘(Matrix-vector Multiplication):矩阵乘以向量然后得到一个新的向量,做法为矩阵的每一个行的元素与向量元素对应相乘再相加。要求矩阵列的维度要和向量维度一致。例如:
[ 1 3 4 0 2 1 ] [ 1 5 ] = [ 1 × 1 + 3 × 5 4 × 1 + 0 × 5 2 × 1 + 1 × 5 ] = [ 16 4 7 ] \begin{bmatrix} 1 & 3 \\ 4 & 0 \\ 2 & 1\\ \end{bmatrix} \begin{bmatrix} 1 \\ 5 \\ \end{bmatrix} = \begin{bmatrix} 1\times 1+3\times 5\\ 4\times1+ 0\times5\\ 2\times1+1\times5\\ \end{bmatrix} = \begin{bmatrix} 16\\ 4\\ 7\\ \end{bmatrix} ⎣⎡142301⎦⎤[15]=⎣⎡1×1+3×54×1+0×52×1+1×5⎦⎤=⎣⎡1647⎦⎤
3.3 矩阵与矩阵相乘(Matrix-matrix Multiplication)
矩阵与矩阵相乘(Matrix-matrix Multiplication):两个矩阵相乘得到一个新的矩阵,做法为第1个矩阵的 i i i 行与第2个矩阵的 j j j 列对应元素相乘再相加作为结果矩阵的第 i i i行第 j j j列的元素。要求第一个矩阵的列数要与第二个矩阵的行数一致。例如:
[ 1 3 2 4 0 1 ] [ 1 3 0 1 5 2 ] = [ 1 × 1 + 3 × 0 + 2 × 5 1 × 3 + 3 × 1 + 2 × 2 4 × 1 + 0 × 0 + 1 × 5 4 × 3 + 0 × 1 + 1 × 2 ] = [ 11 10 9 14 ] \begin{bmatrix} 1 & 3 & 2\\ 4 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 3\\ 0 & 1\\ 5 & 2\\ \end{bmatrix} = \begin{bmatrix} 1 \times 1+3\times 0+2\times 5 & 1\times 3+3\times 1+2\times 2\\ 4\times 1+0\times 0+1\times 5 & 4\times 3+0\times 1+1\times 2\\ \end{bmatrix} = \begin{bmatrix} 11 & 10\\ 9 & 14 \\ \end{bmatrix} [143021]⎣⎡105312⎦⎤=[1×1+3×0+2×54×1+0×0+1×51×3+3×1+2×24×3+0×1+1×2]=[1191014]
3.4 矩阵乘法的性质(Matrix Multiplication Properties)
- A × B ≠ B × A A\times B \neq B\times A A×B=B×A
- ( A × B ) × C = A × ( B × C ) (A\times B) \times C = A\times (B \times C) (A×B)×C=A×(B×C)
- n × n n\times n n×n 的矩阵称为方阵(square matrix)
- 对角线全为1,其余全为0的方阵称为单位矩阵(identity matrix),记作 I I I 或 E E E 。 例如:
[ 1 0 0 0 1 0 0 0 1 ] \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{bmatrix} ⎣⎡100010001⎦⎤ - A ⋅ I = I ⋅ A = A A\cdot I=I \cdot A = A A⋅I=I⋅A=A
3.5 矩阵的逆和转置(Inverse and Transpose)
逆矩阵(inverse matrix):如果一个矩阵 A A A 为方阵,且存在矩阵 B B B,满足 A B = B A = I AB=BA=I AB=BA=I,则称矩阵 B B B 为矩阵 A A A 的逆矩阵,记作 A − 1 A^{-1} A−1 。即 A A − 1 = A − 1 A = I AA^{-1} = A^{-1}A=I AA−1=A−1A=I
逆矩阵的性质:
- 只有方阵才有逆矩阵,且与逆矩阵维度相同
- 不是所有矩阵都有逆矩阵
转置矩阵(transposed matrix):如果一个 m × n m\times n m×n 矩阵 A A A 和另一个 n × m n\times m n×m 的矩阵 B B B ,满足 A i j = B j i A_{ij} = B_{ji} Aij=Bji,则称 B B B 矩阵为 A A A矩阵的转置矩阵,记作 A T A^T AT 。 例如:
A = [ 1 2 0 3 5 9 ] 则 A T = [ 1 3 2 5 0 9 ] A = \begin{bmatrix} 1 & 2 & 0 \\ 3 & 5 & 9 \\ \end{bmatrix} ~~~~~~则 ~~~A^T = \begin{bmatrix} 1 & 3 \\ 2 & 5 \\ 0 & 9 \\ \end{bmatrix} A=[132509] 则 AT=⎣⎡120359⎦⎤
四、多元线性回归(Multivariate Linear Regression)
4.1 多个特征(Multiple features)
多元线性回归:有多个特征的线性回归问题
符号(Notation):
- n n n :表示特征的数量
- x ( i ) x^{(i)} x(i) :第 i i i 个样本的输入
- x j ( i ) x_j^{(i)} xj(i):第 i i i 个样本的第 j j j 个特征的值
多元线性回归方程: h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n h_\theta(x)=\theta_0 + \theta_1x_1 +\theta_2x_2 + \cdots + \theta_nx_n hθ(x)=θ0+θ1x1+θ2x2+⋯+θnxn
为了方便向量化,一般定义 x 0 = 1 x_0=1 x0=1,同时记:
x = [ x 0 x 1 x 2 ⋯ x n ] ∈ R n + 1 θ = [ θ 0 θ 1 θ 2 ⋯ θ n ] ∈ R n + 1 x = \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ \cdots \\ x_n \\ \end{bmatrix} \in \reals ^{n+1} ~~~~~~~~~~~ \theta = \begin{bmatrix} \theta_0 \\ \theta_1 \\ \theta_2 \\ \cdots \\ \theta_n \\ \end{bmatrix}\in \reals ^{n+1} x=⎣⎢⎢⎢⎢⎡x0x1x2⋯xn⎦⎥⎥⎥⎥⎤∈Rn+1 θ=⎣⎢⎢⎢⎢⎡θ0θ1θ2⋯θn⎦⎥⎥⎥⎥⎤∈Rn+1
则,线性回归方程为:
h θ ( x ) = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n = θ T x \begin{aligned} h_\theta(x) &=\theta_0x_0 + \theta_1x_1 +\theta_2x_2 + \cdots + \theta_nx_n \\\\ &= \theta^Tx \end{aligned} hθ(x)=θ0x0+θ1x1+θ2x2+⋯+θnxn=θTx
4.2 多元线性回归中的梯度下降
假设(Hypothesis): h θ ( x ) = θ T x = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n h_\theta(x)= \theta^Tx=\theta_0x_0 + \theta_1x_1 +\theta_2x_2 + \cdots + \theta_nx_n hθ(x)=θTx=θ0x0+θ1x1+θ2x2+⋯+θnxn
参数(Parameters): θ = ( θ 0 , θ 1 , ⋯ , θ n ) T \theta = (\theta_0, \theta_1, \cdots, \theta_n)^T θ=(θ0,θ1,⋯,θn)T
代价函数(Cost function): J ( θ 0 , θ 1 , ⋯ , θ n ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_0, \theta_1, \cdots, \theta_n) = \frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})^2 J(θ0,θ1,⋯,θn)=2m1i=1∑m(hθ(x(i))−y(i))2
梯度下降: R e p e a t { θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) } ( 注 意 要 同 时 更 新 θ j , j = 0 , 1 , ⋯ , n ) \begin{aligned} &Repeat ~~\{ \\ & ~~~~~~~\theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} \\ &\} \\\\ & (注意要同时更新 ~\theta_j,~~~~j=0,1,\cdots, n) \end{aligned} Repeat { θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i)}(注意要同时更新 θj, j=0,1,⋯,n)
4.3 梯度下降实战-特征缩放(Feature Scaling)
问题提出: 若特征的量纲不一致,那么在进行梯度下降的时候,在量纲大的方向上下降过多,而在量纲小的方向下降过少。例如:
- x 1 x_1 x1 = 房屋面积 (0 - 2000 m2)
- x 2 x_2 x2 = 房间数量 (0-5)
特征缩放(feature scaling):让每一个特征都缩放到 [ − 1 , 1 ] [-1, 1] [−1,1] 之间,即 − 1 ≤ x i ≤ 1 -1\le x_i \le 1 −1≤xi≤1
特征缩放常用方法(参考资料):
- 均值归一化(Mean Normalization) :使用 x i − μ i x_i - \mu_i xi−μi 替换 x i x_i xi,使特征的均值约等于0。公式为: x s c a l e = x − μ S x_{scale} = \frac{x-\mu}{S} xscale=Sx−μ
其中, μ \mu μ 为 x x x 对应特征的平均值,S为特征的范围之差(max-min),S也可以使用标准差。
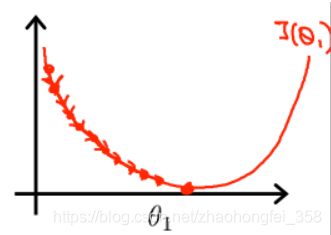
4.4 梯度下降实战-学习率(Learning Rate)
随着梯度下降迭代次数的增多, J ( θ ) J(\theta) J(θ)也会越来越小,曲线大概如下图所示:
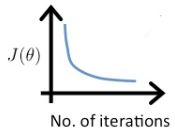
梯度下降的收敛:一般认为,当 J ( θ ) J(\theta) J(θ) 在一次迭代后,减小的量小于 1 0 − 3 10^{-3} 10−3 ,则认为梯度下降已经收敛,可以退出循环了。
学习率 α \alpha α 的总结:
- α \alpha α 太小 : 收敛的太慢
- α \alpha α 太大 :可能会导致不收敛,甚至发散。即每次 J ( θ ) J(\theta) J(θ) 不减反增
学习率 α \alpha α的选择:一般先选择一个很小的数,然后逐渐增大进行尝试。例如: …, 0.001, 0.01, 0.1, 1, …
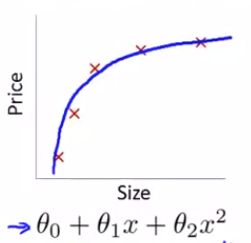
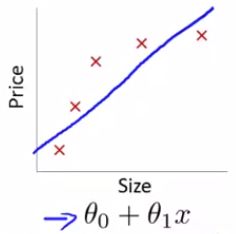
4.5 特征和多项式回归(Features and Polynomial Regression)
由于预测的模型不一定是直线 θ 0 + θ 1 x \theta_0+\theta_1x θ0+θ1x,有可能是二次曲线、三次曲线、…
多项式回归:对一个特征,定义回归方程时,包含特征的高次方。
h θ ( x ) = θ 0 + θ 1 x + θ 2 x 2 + θ 3 x 3 + ⋯ h_\theta(x) = \theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + \cdots hθ(x)=θ0+θ1x+θ2x2+θ3x3+⋯
对于多项式回归方程,处理方式为将x的高次方当成其他特征进行处理即可: x 1 = x , x 2 = x 2 , x 3 = x 3 , . . . x_1 = x ~~,~~~ x_2 = x^2 ~~,~~~ x_3 = x^3 ~~, ~~~ ... x1=x , x2=x2 , x3=x3 , ...
除了定义高次方外,也可以定义其他次方,例如
h θ ( x ) = θ 0 + θ 1 x + θ 2 x 2 + θ 3 x h_\theta(x) = \theta_0 + \theta_1x + \theta_2x^2 + \theta_3\sqrt{x} hθ(x)=θ0+θ1x+θ2x2+θ3x
4.6 正规方程(Normal Equation)
多元线性回归的正规方程解:不使用梯度下降法,而是通过数学公式,直接计算出 θ \theta θ
设有 m m m 个样本 ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , ⋯ , ( x ( m ) , y ( m ) ) (x^{(1)},y^{(1)}), (x^{(2)},y^{(2)}),\cdots, (x^{(m)},y^{(m)}) (x(1),y(1)),(x(2),y(2)),⋯,(x(m),y(m)),每个样本有 n n n 个特征,即:
x ( i ) = [ x 0 ( i ) x 1 ( i ) x 2 ( i ) ⋯ x n ( i ) ] ∈ R n + 1 X = [ ( x ( 1 ) ) T ( x ( 2 ) ) T ( x ( 3 ) ) T ⋯ ( x ( m ) ) T ] m × ( n + 1 ) x^{(i)} = \begin{bmatrix} x_0^{(i)} \\ x_1^{(i)} \\ x_2^{(i)} \\ \cdots \\ x_n^{(i)} \\ \end{bmatrix} \in \R^{n+1} ~~~~~~~~X = \begin{bmatrix} (x^{(1)})^T \\ (x^{(2)})^T \\ (x^{(3)})^T \\ \cdots \\ (x^{(m)})^T \\ \end{bmatrix}_{m\times (n+1)} x(i)=⎣⎢⎢⎢⎢⎢⎡x0(i)x1(i)x2(i)⋯xn(i)⎦⎥⎥⎥⎥⎥⎤∈Rn+1 X=⎣⎢⎢⎢⎢⎡(x(1))T(x(2))T(x(3))T⋯(x(m))T⎦⎥⎥⎥⎥⎤m×(n+1)
则,使得 J ( θ ) J(\theta) J(θ) 最小的 θ \theta θ 为:
θ = ( X T X ) − 1 X T y \theta = (X^T X)^{-1} X^Ty θ=(XTX)−1XTy
时间复杂度:O(n3) ,n为特征数
梯度下降法与正规方程法的比较:
| 梯度下降法 | 正规方程法 |
|---|---|
| 需要考虑学习率 α \alpha α | 不需要选择学习率 |
| 需要多次迭代 | 需需要迭代 |
| 适用于特征比较多的场景,即 n 比较大 | 不适用与特征多的场景 |
4.7 正规方程不可逆(Normal Equation Noninvertibility)
在使用正规方程求解 θ \theta θ 时,有可能出现 X T X X^TX XTX 没有逆矩阵的情况。
主要有以下情况:
1.当特征中存在成比例的特征,则会导致不可逆(会导致 ∣ X ∣ = 0 |X|=0 ∣X∣=0),例如:
- x 1 x_1 x1 = 房屋面积(m2)
- x 2 x_2 x2 = 房屋面积 (亩)
解决方案:只保留一个
2.特征太多了,导致 n ≥ m n\ge m n≥m
解决方案:删除部分特征,或使用正则化(regularization)
五、Octave教程
略,现在不用学这个了,直接用Numpy不香么
六、逻辑回归
6.1 分类问题(Classification)
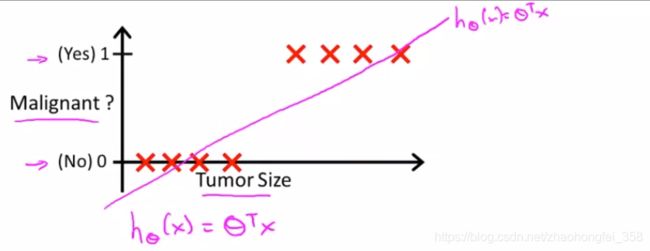
二分类问题:分类结果只包含两种类别,使用 0 , 1 0,1 0,1 表示,即 y ∈ { 0 , 1 } y\in \{0,1\} y∈{0,1}。 其中 0 代表 Negative Class(例如良性肿瘤),1 代表 Positive Class(例如恶性肿瘤)。 具体0,1谁表示什么无所谓。
只使用线性回归处理的弊端:
- 如果 h θ ( x ) ≥ 0.5 h_\theta(x) \ge 0.5 hθ(x)≥0.5 ,预测 y = 1 y=1 y=1
- 如果 h θ ( x ) < 0.5 h_\theta(x) < 0.5 hθ(x)<0.5 ,预测 y = 0 y=0 y=0
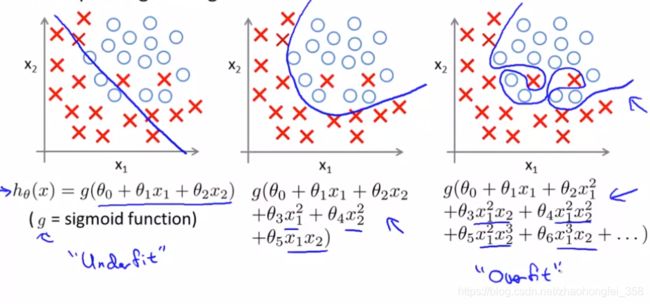
但如果再增加一些极端的点,获得的模型就会如同下面蓝色线,这个模型显然不够好。

而且,线性回归的 h θ ( x ) h_\theta(x) hθ(x) 可能 > 1 >1 >1 也可能 < 0 <0 <0
而逻辑回归满足: 0 ≤ h θ ( x ) ≤ 1 0 \le h_\theta(x) \le 1 0≤hθ(x)≤1
6.2 Hypothesis Representation
逻辑回归是处理二分类问题的
它需要使 0 ≤ h θ ( x ) ≤ 1 0 \le h_\theta(x) \le 1 0≤hθ(x)≤1
逻辑回归模型的假设公式为:
h θ ( x ) = g ( θ T x ) = 1 1 + e − θ T x 其 中 g ( z ) = 1 1 + e − z h_\theta(x) = g(\theta^Tx) =\frac{1}{1+e^{-\theta^Tx}}~~~~~其中 g(z) = \frac{1}{1+e^{-z}} hθ(x)=g(θTx)=1+e−θTx1 其中g(z)=1+e−z1
g ( z ) g(z) g(z) 被称为Sigmoid Function,其函数图像为:

h θ ( x ) h_\theta(x) hθ(x)的结果为对于输入x,使得y=1的概率,即 h θ ( x ) = P ( y = 1 ∣ x ; θ ) h_\theta(x) =P(y=1|x;\theta) hθ(x)=P(y=1∣x;θ) 。例如: h θ ( x ( 1 ) ) = 0.7 h_\theta(x^{(1)}) = 0.7 hθ(x(1))=0.7,表示对于样本 x ( 1 ) x^{(1)} x(1), y = 1 y=1 y=1的概率为0.7
6.3 决策边界(Decision Boundary)
决策边界(Decision Boundary):将数据分成两个类比的边界线。
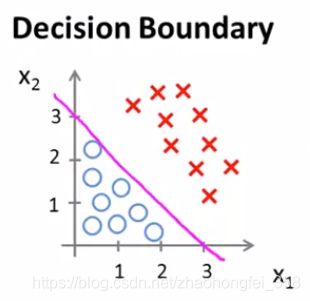
例如,我们经过训练得到了一条决策边界: − 3 + x 1 + x 2 = 0 -3 + x_1+x_2 =0 −3+x1+x2=0
- 当样本 − 3 + x 1 + x 2 ≥ 0 -3 + x_1+x_2 \ge 0 −3+x1+x2≥0 时, g ( − 3 + x 1 + x 2 ) ≥ 0.5 g(-3 + x_1+x_2) \ge 0.5 g(−3+x1+x2)≥0.5 , 预测为红X
- 当样本 − 3 + x 1 + x 2 < 0 -3 + x_1+x_2 <0 −3+x1+x2<0 时, g ( − 3 + x 1 + x 2 ) < 0.5 g(-3 + x_1+x_2) <0.5 g(−3+x1+x2)<0.5 ,预测为蓝〇
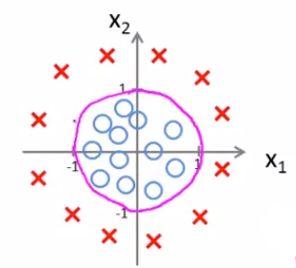
样例2,非线性的决策边界: − 1 + x 1 2 + x 2 2 = 0 -1+x_1^2+x_2^2 = 0 −1+x12+x22=0
- 当 − 1 + x 1 2 + x 2 2 ≥ 0 -1+x_1^2+x_2^2 \ge 0 −1+x12+x22≥0 时, g ( − 1 + x 1 2 + x 2 2 ) ≥ 0.5 g(-1+x_1^2+x_2^2)\ge 0.5 g(−1+x12+x22)≥0.5, 预测为红X
- 当 − 1 + x 1 2 + x 2 2 < 0 -1+x_1^2+x_2^2 < 0 −1+x12+x22<0 时, g ( − 1 + x 1 2 + x 2 2 ) < 0.5 g(-1+x_1^2+x_2^2) < 0.5 g(−1+x12+x22)<0.5, 预测为蓝〇
6.4 逻辑回归的代价函数
逻辑回归的代价函数部分公式如下:
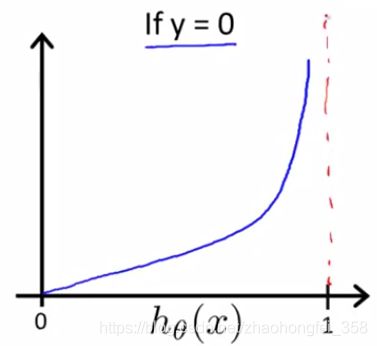
C o s t ( h θ ( x ) , y ) = { − log ( h θ ( x ) ) if y = 1 − log ( 1 − h θ ( x ) ) if y = 0 注意底数是 e , 不 是 2 Cost(h_\theta(x), y) = \begin{cases} -\log(h_\theta(x)) &\text{if } ~~y=1 \\ -\log (1-h_\theta(x)) &\text{if } ~~ y=0 \end{cases}~~~~~~\text{注意底数是} e,不是2 Cost(hθ(x),y)={−log(hθ(x))−log(1−hθ(x))if y=1if y=0 注意底数是e,不是2
− log ( h θ ( x ) ) -\log(h_\theta(x)) −log(hθ(x)) 的函数图像如下,预测结果 h θ ( x ) h_\theta(x) hθ(x) 越偏离真实结果1,那么代价就越大

− log ( 1 − h θ ( x ) ) -\log (1-h_\theta(x)) −log(1−hθ(x)) 的函数图像如下,预测结果 h θ ( x ) h_\theta(x) hθ(x) 越偏离真实结果0,那么代价就越大
6.5 简化代价函数和梯度下降(Simplified Cost Function and Gradient Descent )
梯度下降的代价函数部分公式如下:
C o s t ( h θ ( x ) , y ) = { − log ( h θ ( x ) ) if y = 1 − log ( 1 − h θ ( x ) ) if y = 0 注意底数是 e , 不 是 2 Cost(h_\theta(x), y) = \begin{cases} -\log(h_\theta(x)) &\text{if } ~~y=1 \\ -\log (1-h_\theta(x)) &\text{if } ~~ y=0 \end{cases}~~~~~~\text{注意底数是} e,不是2 Cost(hθ(x),y)={−log(hθ(x))−log(1−hθ(x))if y=1if y=0 注意底数是e,不是2
将其合并为一个式子为:
Cost ( h θ ( x ) , y ) = − y log ( h θ ( x ) ) − ( 1 − y ) log ( 1 − h θ ( x ) ) \operatorname{Cost}\left(h_{\theta}(x), y\right)=-y \log \left(h_{\theta}(x)\right)-(1-y) \log \left(1-h_{\theta}(x)\right) Cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))
完整的线性回归代价函数公式如下:
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J(\theta)=-\frac{1}{m} \sum_{i=1}^{m}\left[y^{(i)} \log \left(h_{\theta}\left(x^{(i)}\right)\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right] J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
对应的梯度下降公式为(详细推导公式):
θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_{j}:=\theta_{j}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)} θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i)
向量化的实现为(向量化过程):
θ : = θ − α m X T ( g ( X θ ) − y ⃗ ) \theta:=\theta-\frac{\alpha}{m} X^{T}(g(X \theta)-\vec{y}) θ:=θ−mαXT(g(Xθ)−y)
6.6 高级优化(Advanced Optimization)
除梯度下降法之外,其他使 θ \theta θ 最优的算法有:
- 共轭梯度(Conjugate gradient)
- BFGS
- L-BFGS
上述算法的优点:
- 不需要手动选择学习率 α \alpha α
- 比梯度下降快
上述算法的缺点:
- 实现复杂
6.7 多分类问题:一对多(Multiclass Classification: One-vs-all)
对于多分类问题,只需要将每个类别分别进行一对多处理即可
为每一个类别 i i i 训练一个逻辑回归模型 h θ ( i ) ( x ) h_\theta^{(i)}(x) hθ(i)(x),用来预测 y = i y=i y=i 的可能性,当需要预测新的输入 x x x 时,使用所有的模型进行预测,选择概率最大的作为预测结果: max i h θ ( i ) ( x ) \max _{i} h_{\theta}^{(i)}(x) maxihθ(i)(x)
h θ ( i ) ( x ) = P ( y = i ∣ x ; θ ) h_{\theta}^{(i)}(x)=P(y=i | x ;~ \theta) hθ(i)(x)=P(y=i∣x; θ)
- 首先,将
X和口,看成一个类别,得到 h θ ( 1 ) ( x ) h_\theta^{(1)}(x) hθ(1)(x)
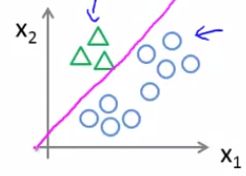
2. 然后,将 △ 和 X 看成一个类别,得到 h θ ( 2 ) ( x ) h_\theta^{(2)}(x) hθ(2)(x)

3. 最后,将 △ 和 口 看成一个类别,得到 h θ ( 3 ) ( x ) h_\theta^{(3)}(x) hθ(3)(x)

七、解决过拟合问题
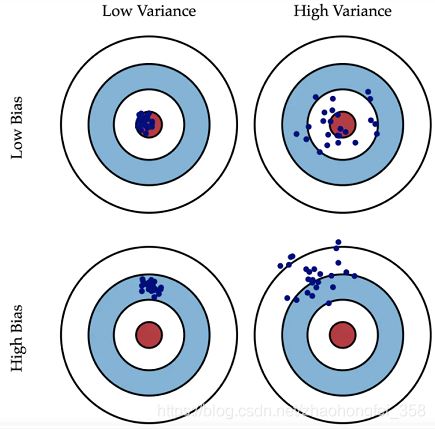
7.1 过拟合问题
过拟合(Overfitting):如果我们特征太多(特征的高次方太多),那样学习的假设函数就可以非常好的拟合,但是却不能很好的进行泛化(预测新的输入)
Overfitting:If we have too many features, the learned hypothesis may fit the training set very well ( J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 ≈ 0 J(\theta)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} \approx 0 J(θ)=2m1∑i=1m(hθ(x(i))−y(i))2≈0 ), but fail to generalize to new examples
过拟合:
- 拟合的太好,不能很好泛化
- 高方差,低偏差
欠拟合:
- 拟合的不够好
- 低方差,高偏差
例如,我们有一个预测房价的模型:
如果假设为直线,就会出现欠拟合(underfit) 问题,它会有较高的偏差(高偏差(High Bias)):
如果假设函数的特征太多,拟合的太好了,反而不好,称为过拟合(overfit),它会有较高的方差(高方差(High Variance)):
理解高偏差和高方差
过拟合的处理:
- 减少特征的数量:①手动选择保留哪些特征 ②使用模型选择算法(Model selection algorithm)
- 正则化(Regularization):①保留所有特征,但是减少参数 θ j \theta_j θj 的量级(magnitude); 当特征比较多时,该方法就比较好了,因为每一个特征都为预测 y y y 贡献了自己的一点力量
7.2 包含正则化的代价函数
正则化(Regularization)的目的:
- 防止过拟合
- 简化假设模型(“Simpler” hypothesis)
正则化的实现思路:为每个一 θ j \theta_j θj 增加一个惩罚,让每个 θ j \theta_j θj 都变小一点,这样最后的曲线就相对圆滑
正则化的代价函数公式:
J ( θ ) = 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 ] J(\theta)=\frac{1}{2 m}\left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\lambda \sum_{j=1}^{n} \theta_{j}^{2}\right] J(θ)=2m1[i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2]
其中 λ \lambda λ 被称为正则化参数(Regularization Paramter) 是一个常数
注意:正则化是从 θ 1 \theta_1 θ1 开始,因为 θ 0 \theta_0 θ0 是截距,不用参与正则化
λ \lambda λ 不能过大,如果过大,对每一个 θ j \theta_j θj 的惩罚太大,最后他们全成0了,最后就会欠拟合,例如:
7.3 正则化的线性回归(Regularized Linear Regression)
正则化的代价函数公式:
J ( θ ) = 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 ] J(\theta)=\frac{1}{2 m}\left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\lambda \sum_{j=1}^{n} \theta_{j}^{2}\right] J(θ)=2m1[i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2]
无正则化的梯度下降公式:
R e p e a t { θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) } \begin{aligned} &Repeat ~~\{ \\ & ~~~~~~~\theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} \\ &\} \\\\ \end{aligned} Repeat { θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i)}
正则化后的梯度下降公式:
R e p e a t { θ j : = θ j − α [ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] } \begin{aligned} &Repeat ~~\{ \\ & ~~~~~~~\theta_j := \theta_j - \alpha \left[ \frac{1}{m} \sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} +\frac{\lambda}{m} \theta_j \right] \\ &\} \\\\ \end{aligned} Repeat { θj:=θj−α[m1i=1∑m(hθ(x(i))−y(i))xj(i)+mλθj]}
整理后得:
θ j : = θ j ( 1 − α λ m ) − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_{j}:=\theta_{j}\left(1-\alpha \frac{\lambda}{m}\right)-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)} θj:=θj(1−αmλ)−αm1i=1∑m(hθ(x(i))−y(i))xj(i)
要保证 ( 1 − α λ m ) \left(1-\alpha \frac{\lambda}{m}\right) (1−αmλ) < 1,这样才能起到惩罚的作用,每次让 θ j \theta_j θj 减少的更多一点
无正则化的线性回归正规方程解:
θ = ( X T X ) − 1 X T y \theta = (X^T X)^{-1} X^Ty θ=(XTX)−1XTy
正则化后的线性回归正规方程解:
θ = ( X T X + λ [ 0 1 1 ⋱ 1 ] ) − 1 X T y \theta=\left(X^{T} X+\lambda\left[\begin{array}{llll} 0 & & & \\ & 1 & & \\ & & 1 & & \\ & & & \ddots & \\ & & & & 1\\ \end{array}\right]\right)^{-1} X^{T} y θ=⎝⎜⎜⎜⎜⎛XTX+λ⎣⎢⎢⎢⎢⎡011⋱1⎦⎥⎥⎥⎥⎤⎠⎟⎟⎟⎟⎞−1XTy
7.4 正则化的逻辑回归(Regularized Logistic Regression)
正则化后的逻辑回归的代价函数为:
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta)=-\frac{1}{m} \sum_{i=1}^{m}\left[y^{(i)} \log \left(h_{\theta}\left(x^{(i)}\right)\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right] + \frac{\lambda}{2m} \sum_{j=1}^n \theta_j^2 J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2
无正则化的逻辑回归的梯度下降公式:
θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_{j}:=\theta_{j}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)} θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i)
正则化后的逻辑回归的梯度下降公式:
θ j : = θ j − α [ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] \theta_{j}:=\theta_{j}-\alpha \left[ \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)} + \frac{\lambda}{m} \theta_j \right] θj:=θj−α[m1i=1∑m(hθ(x(i))−y(i))xj(i)+mλθj]
八、神经网络(Neural Networks)
8.1 非线性假设(Non-linear Hypotheses)
线性假设的弊端:特征太多了
假设现在预测房价模型:
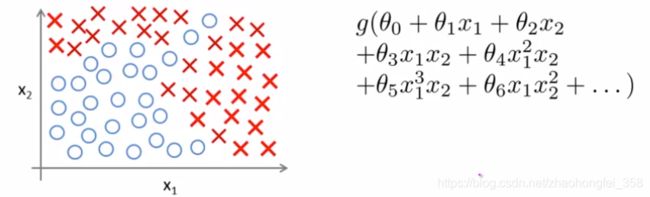
使用逻辑回归模型,假设函数为右侧。我们有两个特征 x 1 , x 2 x_1 , x_2 x1,x2,模型特征却有 x 1 , x 2 , x 1 x 2 , . . . x_1,x_2,x_1x_2,... x1,x2,x1x2,... 无数个。
如果有100个特征,次方弄到2,那么最终的模型特征数量就总共有5150个特征,分别是 x 1 , x 2 , ⋯ , x 100 , x 1 2 , x 1 x 2 , ⋯ , x 1 x 100 , x 2 2 , x 2 x 3 , ⋯ , x 2 x 100 , ⋯ , x 100 2 x_1, x_2, \cdots, x_{100}, x_1^2, x_1x_2, \cdots,x_1x_{100},x_2^2,x_2x_3,\cdots,x_2x_{100},\cdots,x_{100}^2 x1,x2,⋯,x100,x12,x1x2,⋯,x1x100,x22,x2x3,⋯,x2x100,⋯,x1002
如果有100个特征,次方弄到3,最终会约有17w个模型特征。
所以,要提出非线性的模型假设
8.2 神经和大脑(Neurons and the Brain)
科普,可略
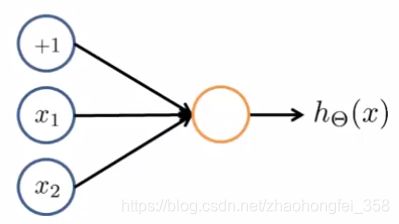
8.3 模型表示(Model Representation)

Dendrite(树突): 从树突输入数据
Nucleus(细胞核):由细胞核处理数据
Axon(轴突):通过轴突输出处理结果,或将处理结果反馈到下一层继续处理
神经网是以上述为思路构建的。
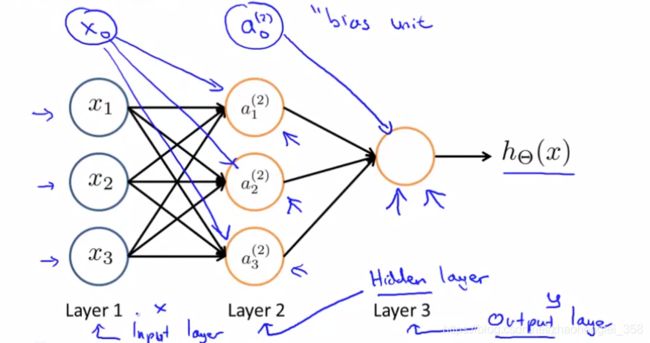
- x 1 , x 2 , x 3 x_1, x_2, x_3 x1,x2,x3: 输入的特征值。 x 1 x_1 x1上面还有一个 x 0 x_0 x0,称为偏置单元(Bias Unit),恒等于1。
- 激活函数(activation function):橙色的圈为激活函数,一般选用Sigmoid函数
- h θ ( x ) h_\theta (x) hθ(x):模型的输出
- 权重(weight): x 1 x_1 x1 到
激活函数之间的那条线,也就是 θ j \theta_j θj,在神经网络中,称为权重(weight)
- 输入层(Input Layer):Layer 1,数据从该层输入
- 隐藏层(Hidden Layer):Layer 2 到 Layer L-1,(L为层数),在第二层到最后一层之间的层称为隐藏层。隐藏层的每一个结点都是一个激活函数
- 输出层(Output Layer):Layer L,最后一层,该层得到的结果为输出结果
符号表示:
- a i ( j ) a_i^{(j)} ai(j) : 在第 j j j 层的第 i i i 个激活单元
- Θ ( j ) \Theta^{(j)} Θ(j):控制从 j j j 层 到 j + 1 j+1 j+1 层函数映射的矩阵的权重矩阵。 Θ ( j ) \Theta^{(j)} Θ(j) 的维数:如果神经网络的 j j j层有 s j s_j sj 个单元(units), j + 1 j+1 j+1 层有 s j + 1 s_{j+1} sj+1 个单元,那么 Θ ( j ) \Theta^{(j)} Θ(j) 是 s j + 1 × ( s j + 1 ) s_{j+1} \times (s_j + 1) sj+1×(sj+1) 维的
- Θ k , i ( j ) \Theta^{(j)}_{k,i} Θk,i(j):第 j j j 层,第 k k k 个结点的第 i i i 个权重的值
神经网络的向量化:
令 x = [ x 0 x 1 ⋯ x n ] z ( j ) = [ z 1 ( j ) z 2 ( j ) ⋯ z n ( j ) ] 令 ~~~~x=\left[\begin{array}{c} x_{0} \\ x_{1} \\ \cdots \\ x_{n} \end{array}\right]~~~~~ z^{(j)}=\left[\begin{array}{c} z_{1}^{(j)} \\ z_{2}^{(j)} \\ \cdots \\ z_{n}^{(j)} \end{array}\right] 令 x=⎣⎢⎢⎡x0x1⋯xn⎦⎥⎥⎤ z(j)=⎣⎢⎢⎢⎡z1(j)z2(j)⋯zn(j)⎦⎥⎥⎥⎤
则有:
z ( j ) = Θ ( j − 1 ) a ( j − 1 ) a ( j ) = g ( z ( j ) ) h Θ ( x ) = a ( j + 1 ) = g ( z ( j + 1 ) ) \begin{aligned} z^{(j)} & =\Theta^{(j-1)} a^{(j-1)} \\\\ a^{(j)} &= g(z^{(j)}) \\\\ h_{\Theta}(x) &=a^{(j+1)}=g\left(z^{(j+1)}\right) \end{aligned} z(j)a(j)hΘ(x)=Θ(j−1)a(j−1)=g(z(j))=a(j+1)=g(z(j+1))
例如,对于上面的神经网络,有:
a 1 ( 2 ) = g ( Θ 10 ( 1 ) x 0 + Θ 11 ( 1 ) x 1 + Θ 12 ( 1 ) x 2 + Θ 13 ( 1 ) x 3 ) a 2 ( 2 ) = g ( Θ 20 ( 1 ) x 0 + Θ 21 ( 1 ) x 1 + Θ 22 ( 1 ) x 2 + Θ 23 ( 1 ) x 3 ) a 3 ( 2 ) = g ( Θ 30 ( 1 ) x 0 + Θ 31 ( 1 ) x 1 + Θ 32 ( 1 ) x 2 + Θ 33 ( 1 ) x 3 ) h Θ ( x ) = a 1 ( 3 ) = g ( Θ 10 ( 2 ) a 0 ( 2 ) + Θ 11 ( 2 ) a 1 ( 2 ) + Θ 12 ( 2 ) a 2 ( 2 ) + Θ 13 ( 2 ) a 3 ( 2 ) ) \begin{aligned} a_{1}^{(2)} &=g\left(\Theta_{10}^{(1)} x_{0}+\Theta_{11}^{(1)} x_{1}+\Theta_{12}^{(1)} x_{2}+\Theta_{13}^{(1)} x_{3}\right) \\\\ a_{2}^{(2)} &=g\left(\Theta_{20}^{(1)} x_{0}+\Theta_{21}^{(1)} x_{1}+\Theta_{22}^{(1)} x_{2}+\Theta_{23}^{(1)} x_{3}\right) \\\\ a_{3}^{(2)} &=g\left(\Theta_{30}^{(1)} x_{0}+\Theta_{31}^{(1)} x_{1}+\Theta_{32}^{(1)} x_{2}+\Theta_{33}^{(1)} x_{3}\right) \\\\ h_{\Theta}(x) &=a_{1}^{(3)}=g\left(\Theta_{10}^{(2)} a_{0}^{(2)}+\Theta_{11}^{(2)} a_{1}^{(2)}+\Theta_{12}^{(2)} a_{2}^{(2)}+\Theta_{13}^{(2)} a_{3}^{(2)}\right) \end{aligned} a1(2)a2(2)a3(2)hΘ(x)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)=a1(3)=g(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))
将其向量化,可以表示为如下:
z ( 2 ) = Θ ( 1 ) x = Θ ( 1 ) a ( 1 ) a ( 2 ) = g ( z ( 2 ) ) 其 中 x = [ x 0 x 1 x 2 x 3 ] z ( 2 ) = [ z 1 ( 2 ) z 2 ( 2 ) z 3 ( 2 ) ] \begin{aligned} z^{(2)} & = \Theta^{(1)} x = \Theta^{(1)} a^{(1)} \\\\ a^{(2)} & = g(z^{(2)}) \\ \end{aligned} ~~~~~~~其中~~ x=\left[\begin{array}{l} x_{0} \\ x_{1} \\ x_{2} \\ x_{3} \end{array}\right] \quad~~ z^{(2)}=\left[\begin{array}{c} z_{1}^{(2)} \\\\ z_{2}^{(2)} \\\\ z_{3}^{(2)} \end{array}\right] z(2)a(2)=Θ(1)x=Θ(1)a(1)=g(z(2)) 其中 x=⎣⎢⎢⎡x0x1x2x3⎦⎥⎥⎤ z(2)=⎣⎢⎢⎢⎢⎢⎡z1(2)z2(2)z3(2)⎦⎥⎥⎥⎥⎥⎤
第三层为:
增 加 偏 置 节 点 a 0 ( 2 ) = 1 z 3 = Θ ( 2 ) a ( 2 ) h Θ ( x ) = a ( 3 ) = g ( z ( 3 ) ) \begin{aligned} & 增加偏置节点 ~~~a_0^{(2)} = 1\\\\ & z^{3} = \Theta^{(2)}a^{(2)}\\\\ & h_\Theta(x) = a^{(3)} = g(z^{(3)}) \end{aligned} 增加偏置节点 a0(2)=1z3=Θ(2)a(2)hΘ(x)=a(3)=g(z(3))
8.4 样例1(Examples and Intuitions)
假设,我们要构建模型来预测 y = x 1 AND x 2 ~~~~~~y = x_1~ \text{AND}~ x_2~~~~~~~~~ y=x1 AND x2 (1&1 = 1, 0&1 = 0, 0&0=0)
我们可以构架纳入下神经网络:
通过机器学习,我们得到了 Θ ( 1 ) = ( − 30 , + 20 , + 20 ) T \Theta^{(1)} =(-30, +20, +20)^T Θ(1)=(−30,+20,+20)T,即:
将 x 1 , x 2 x_1, x_2 x1,x2 代入 sigmoid 函数,可得:
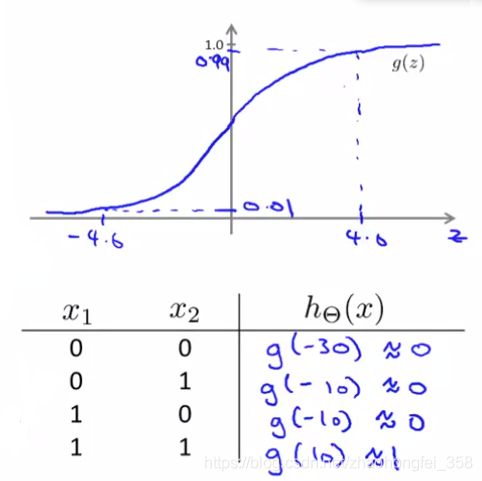
可以看出,我们预测的模型是正确的,可以满足一开始的预期 y = x 1 AND x 2 y = x_1~ \text{AND}~ x_2 y=x1 AND x2
同理,也可以构建 OR Function 的神经网络模型,如下:

8.5 多分类问题(Multiclass Classification)
上述例子为二分类问题,这样输出 y ∈ { 0 , 1 } y \in \{0,1\} y∈{0,1},这样只需要用一个输出结点即可。
如果是一对多问题,例如:

我们需要将图片分成如下4个类别,则相应神经网络的输出结点应该是4个:
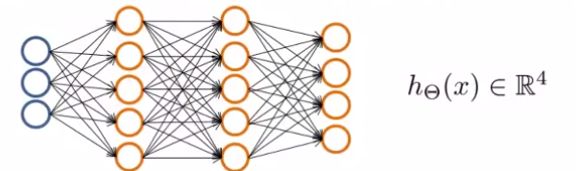
当为Pedestrian时: h Θ ( x ) ≈ [ 1 0 0 0 ] , 当为Car时: h Θ ( x ) ≈ [ 0 1 0 0 ] , 当为Motorcycle时: h Θ ( x ) ≈ [ 0 0 1 0 ] , etc. \begin{aligned} &\text { 当为Pedestrian时: } h_{\Theta}(x) \approx\left[\begin{array}{l} 1 \\ 0 \\ 0 \\ 0 \end{array}\right],~~~ \text { 当为Car时:}h_{\Theta}(x) \approx\left[\begin{array}{l} 0 \\ 1 \\ 0 \\ 0 \end{array}\right], \text { 当为Motorcycle时:} h_{\Theta}(x) \approx\left[\begin{array}{l} 0 \\ 0 \\ 1 \\ 0 \end{array}\right], \text { etc. }\\ \end{aligned} 当为Pedestrian时: hΘ(x)≈⎣⎢⎢⎡1000⎦⎥⎥⎤, 当为Car时:hΘ(x)≈⎣⎢⎢⎡0100⎦⎥⎥⎤, 当为Motorcycle时:hΘ(x)≈⎣⎢⎢⎡0010⎦⎥⎥⎤, etc.
九、神经网络(二)
9.1 代价函数
- L = L = L= 神经网络的层数。在上图中 L = 4 L=4 L=4
- s l = s_l = sl= l l l 层的结点个数(不计算偏置节点(bias unit))。上图中, s 1 = 3 , s 2 = s 3 = 5 , s 4 = s L = 4 s_1=3,s_2=s_3=5,s_4=s_L=4 s1=3,s2=s3=5,s4=sL=4
- K K K = 多分类问题的类别数量。输出维度为 y ∈ R K y\in \reals^K y∈RK 。如果是二分类问题,结果为0,1,此时 y ∈ { 0 , 1 } y\in \{0,1\} y∈{0,1}
逻辑回归的代价函数如下:
J ( θ ) = − 1 m [ ∑ i = 1 m y ( i ) log h θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta)=-\frac{1}{m}\left[\sum_{i=1}^{m} y^{(i)} \log h_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]+\frac{\lambda}{2 m} \sum_{j=1}^{n} \theta_{j}^{2} J(θ)=−m1[i=1∑my(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2
神经网络的代价函数如下:
J ( Θ ) = − 1 m [ ∑ i = 1 m ∑ k = 1 K y k ( i ) log ( h Θ ( x ( i ) ) ) k + ( 1 − y k ( i ) ) log ( 1 − ( h Θ ( x ( i ) ) ) k ) ] + λ 2 m ∑ l = 1 L − 1 ∑ i = 1 s l ∑ j = 1 s l + 1 ( Θ j i ( l ) ) 2 \begin{aligned} J(\Theta)= & -\frac{1}{m}\left[\sum_{i=1}^{m} \sum_{k=1}^{K} y_{k}^{(i)} \log \left(h_{\Theta}\left(x^{(i)}\right)\right)_{k}+\left(1-y_{k}^{(i)}\right) \log \left(1-\left(h_{\Theta}\left(x^{(i)}\right)\right)_{k}\right)\right] \\\\ &+\frac{\lambda}{2 m} \sum_{l=1}^{L-1} \sum_{i=1}^{s_{l}} \sum_{j=1}^{s_{l+1}}\left(\Theta_{j i}^{(l)}\right)^{2} \end{aligned} J(Θ)=−m1[i=1∑mk=1∑Kyk(i)log(hΘ(x(i)))k+(1−yk(i))log(1−(hΘ(x(i)))k)]+2mλl=1∑L−1i=1∑slj=1∑sl+1(Θji(l))2
其中:
h Θ ( x ) ∈ R K ( h Θ ( x ) ) k = k t h output ( 第 k 个 类 别 的 输 出 值 ) h_{\Theta}(x) \in \mathbb{R}^{K} \quad\left(h_{\Theta}(x)\right)_{k}=k^{t h} \text { output } (第k个类别的输出值)\\ hΘ(x)∈RK(hΘ(x))k=kth output (第k个类别的输出值)
注意: ∑ i = 1 s l ∑ j = 1 s l + 1 \sum_{i=1}^{s_{l}} \sum_{j=1}^{s_{l+1}} ∑i=1sl∑j=1sl+1 分别是 S l S_l Sl 和 S l + 1 S_{l+1} Sl+1 ,而不是 s l sl sl 和 s l + 1 s_l +1 sl+1
公式解释:
- 上半部分和逻辑回归类似,但不一样的地方在 ∑ k = 1 K \sum_{k=1}^{K} ∑k=1K 。在逻辑回归的二分类中, y ∈ { 0 , 1 } y \in \{0,1\} y∈{0,1},其中 log h θ ( x ( i ) ) \log h_{\theta}\left(x^{(i)}\right) loghθ(x(i)) 计算 y = 1 y=1 y=1 的部分, ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) \left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right) (1−y(i))log(1−hθ(x(i)))计算 y = 0 y=0 y=0 的部分。而在多分类问题, y ∈ R K y\in \reals^K y∈RK, 也就是有K个 { 0 , 1 } \{0,1\} {0,1},这样在计算代价函数时,要把这 K K K 种结果求和
- 下半部分是参数正则化。对于逻辑回归,只有 n n n 个 θ j \theta_j θj 需要进行正则化。但在神经网络中就多了,因为有 L L L 层,所以需要遍历 1 1 1 到 L − 1 L-1 L−1 层(最后一层为输出层,所以就没有线( θ \theta θ)了),所以就有了 ∑ l = 1 L − 1 \sum_{l=1}^{L-1} ∑l=1L−1 。 对于 l l l层,因为有 s l s_l sl 个结点(不算偏置结点),所以就有了 ∑ i = 1 s l \sum_{i=1}^{s_{l}} ∑i=1sl 。 而 l l l 层的每一个结点都要与它的下一层( s l + 1 s_{l+1} sl+1层)结点连条线(每条线代表一个 Θ j i ( l ) \Theta_{ji}^{(l)} Θji(l) 权重),所以就有了 ∑ j = 1 s l + 1 \sum_{j=1}^{s_{l+1}} ∑j=1sl+1
9.2 反向传播算法(Backpropagation Algorithm)
反向传播算法的用途:计算出 Θ \Theta Θ
与其他算法一致,我们得到了代价函数 J ( Θ ) J(\Theta) J(Θ),目标是最小化 J ( Θ ) J(\Theta) J(Θ),即
min Θ J ( Θ ) \min _{\Theta} J(\Theta) ΘminJ(Θ)
所以需要编码来计算:
- J ( Θ ) J(\Theta) J(Θ)
- ∂ ∂ Θ i j ( l ) J ( Θ ) \frac{\partial}{\partial \Theta_{ij}^{(l)}}J(\Theta) ∂Θij(l)∂J(Θ)
正向传播算法的用途:给定权重 Θ \Theta Θ 和 输入 x x x,求出输出 h Θ ( x ) h_\Theta(x) hΘ(x)
正向传播算法思路:从输入层开始,一层一层计算,最终得出输出结果
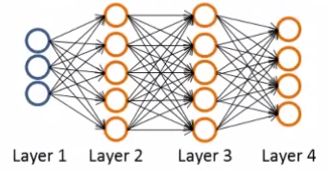
例如,对于该神经网络,使用正向传播算法计算 h Θ ( x ) h_\Theta(x) hΘ(x) 的过程如下:
a ( 1 ) = x z ( 2 ) = Θ ( 1 ) a ( 1 ) a ( 2 ) = g ( z ( 2 ) ) ( add a 0 ( 2 ) ) z ( 3 ) = Θ ( 2 ) a ( 2 ) a ( 3 ) = g ( z ( 3 ) ) ( add a 0 ( 3 ) ) z ( 4 ) = Θ ( 3 ) a ( 3 ) a ( 4 ) = h Θ ( x ) = g ( z ( 4 ) ) \begin{aligned} a^{(1)} &=x \\ z^{(2)} &=\Theta^{(1)} a^{(1)} \\ a^{(2)} &=g\left(z^{(2)}\right) \quad\left(\operatorname{add} a_{0}^{(2)}\right) \\ z^{(3)} &=\Theta^{(2)} a^{(2)} \\ a^{(3)} &=g\left(z^{(3)}\right)\left(\operatorname{add} a_{0}^{(3)}\right) \\ z^{(4)} &=\Theta^{(3)} a^{(3)} \\ a^{(4)} &=h_{\Theta}(x)=g\left(z^{(4)}\right) \end{aligned} a(1)z(2)a(2)z(3)a(3)z(4)a(4)=x=Θ(1)a(1)=g(z(2))(adda0(2))=Θ(2)a(2)=g(z(3))(adda0(3))=Θ(3)a(3)=hΘ(x)=g(z(4))
以 a ( 4 ) a^{(4)} a(4) 为例,将其展开:
a ( 4 ) = g ( z ( 4 ) ) = g ( Θ ( 3 ) a ( 3 ) ) = g ( [ Θ 10 ( 3 ) a 0 ( 3 ) + Θ 11 ( 3 ) a 1 ( 3 ) + ⋯ + Θ 15 ( 3 ) a 5 ( 3 ) Θ 20 ( 3 ) a 0 ( 3 ) + Θ 21 ( 3 ) a 1 ( 3 ) + ⋯ + Θ 25 ( 3 ) a 5 ( 3 ) Θ 30 ( 3 ) a 0 ( 3 ) + Θ 31 ( 3 ) a 1 ( 3 ) + ⋯ + Θ 35 ( 3 ) a 5 ( 3