深度学习基础知识点（一）CNN卷积神经网络——1.卷积方面的原理

目录

1.感受野受哪几个参数的影响，计算感受野的大小 ？

2.上采样方式subpixel，反卷积，resize

3.卷积核大小为什么是奇数？

4.CNN为什么参数共享?

5.Dropout是什么？为什么Dropout可以防止过拟合？

Dropout具体工作流程

Dropout在测试时需要怎么补偿？

为什么说Dropout可以解决过拟合？

6.CNN的平移不变怎么体现？

7.为什么CNN比DNN在图像领域更具优势？

---

1.感受野受哪几个参数的影响，计算感受野的大小 ？

关于感受野的总结 - 知乎

感受野被定义为卷积神经网络特征所能看到输入图像的区域，换句话说特征输出受感受野区域内的像素点的影响。

比如下图（该图为了方便，将二维简化为一维），这个三层的神经卷积神经网络，每一层卷积核的_ = 3 ， = 1，那么最上层特征所对应的感受野就为如图所示的7x7。

计算方式：

如果有dilated conv的话，计算公式为：

2.上采样方式subpixel，反卷积，resize

subpixel：亚像素卷积，是一种正常卷积的简化形式，并加了很强的假设，结果就是去除了大量的卷积运算。结果一般是一张更大的图片，可用作超分辨率。

一个正常的反/逆/转置卷积如下：

把一个3x3的小图片变成一个5X5的大图片。白色虚线区域全填0。subpixel作者认为，这些白色的填0区域，是无效信息，甚至对求梯度优化有害处。明明可以直接从原图得到信息，何必非要填0呢。于是作者搞了这个：

第一个白色矩阵图片是输入层。第二个、第三个白色张量是隐藏层，做步长为1的正常卷积。第四个彩色图片，经过子像素卷积，得到最后一张斑斓的大图。

PixelShuffle(像素重组)的主要功能是将低分辨的特征图，通过卷积和多通道间的重组得到⾼分辨率的特征图。这⼀⽅法最初是为了解决图像超分辨率问题⽽提出的，这种称为Sub-Pixel Convolutional Neural Network的⽅法成为了上采样的有效⼿段。
要把⼀张低分辨输⼊转变为⾼分辨输出，论⽂ESPCN中提出⽤基于特征抽取和亚像素卷积的⽅法来扩⼤特征图，将特征图从低分辨空间转换到⾼分辨空间中去。
上图中左侧第⼀部分是⽤于对图像的特征进⾏抽取。⽽后在倒数第⼆层⽣成 r*r 个通道特征图，这⾥ r 就是希望上采样的倍数。
pixelshuffle的主要功能就是将这 r*r 个通道的特征图组合为新的 w*r,h*r 的上采样结果。具体来说，就是将原来⼀个低分辨的像素划分为r*r个更⼩的格⼦，利⽤r*r个特征图对应位置的值按照⼀定的规则来填充这些⼩格⼦。按照同样的规则将每个低分辨像素划分出的⼩格⼦填满就完成了重组过程。在这⼀过程中模型可以调整 r*r 个shuffle通道权重 不断优化⽣成的结果。
主要实现了这样的功能：N * (C * r * r) * W * H  →  N * C * (H * r) * (W * r)
利⽤这些⽅法可以来改进特征图上采样过程中出现的问题，特别是在图像超分辨和图像增强的算法中需要对特征图进⾏上下采样的过程，可以解决插值和解卷积的⼀些⼈⼯痕迹问题。

最上面一排是输入的模糊图像x。中间是超分辨后的图片f(x)。最下面是对照样例y。

3.卷积核大小为什么是奇数？

• 奇数卷积核更容易做padding。我们假设卷积核大小为k*k，为了让卷积后的图像大小与原图一样大，根据公式可得到padding=（k-1）/2，k只有在取奇数的时候，padding才能是整数，就可以从图像的两边对称padding，否则不好进行图片填充。
• 保护位置信息。在CNN中，一般会以卷积核的某个点进行窗口滑动，通常这个基准点是卷积核的中心点。奇数有central pixel，保证了锚点刚好在中间，方便以模块中心为标准进行滑动卷积，避免了位置信息发生偏移 。由于奇数核拥有天然的绝对中心点，因此也可以更好地获取中心信息。

4.CNN为什么参数共享?

权值共享 : 卷积核的参数实际上也可以叫做权重，它描述了局部连接中该位置的输入对于相应输出的影响力（重要性）。

一个卷积层中可以有多个不同的卷积核，而每一个卷积核都对应着一个滤波后映射出的新图像(Feature map)，同一个新图像的所有像素全部来自于同一个卷积核，这就是卷积核的参数共享。

卷积中不做参数共享，则每一个输出对应一组参数值，参数量仍然庞大。

5.Dropout是什么？为什么Dropout可以防止过拟合？

深度学习中Dropout原理解析 - 知乎

Dropout：在每个训练批次中，通过忽略一半的特征检测器（让一半的隐层节点值为0），可以明显地减少过拟合现象。这种方式可以减少特征检测器（隐层节点）间的相互作用，检测器相互作用是指某些检测器依赖其他检测器才能发挥作用。

Dropout说的简单一点就是：我们在前向传播的时候，让某个神经元的激活值以一定的概率p停止工作，这样可以使模型泛化性更强，因为它不会太依赖某些局部的特征，如下图所示。

Dropout具体工作流程

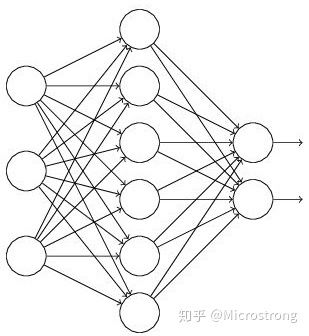
假设我们要训练这样一个神经网络，如下图所示。

输入是x输出是y，正常的流程是：我们首先把x通过网络前向传播，然后把误差反向传播以决定如何更新参数让网络进行学习。使用Dropout之后，过程变成如下：

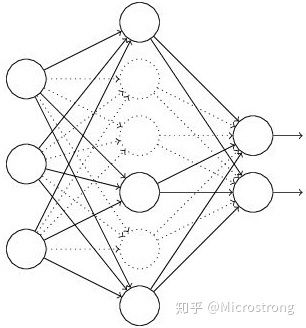
（1）首先随机（临时）删掉网络中一半的隐藏神经元，输入输出神经元保持不变（下图中虚线为部分临时被删除的神经元）

（2） 然后把输入x通过修改后的网络前向传播，然后把得到的损失结果通过修改的网络反向传播。一小批训练样本执行完这个过程后，在没有被删除的神经元上按照随机梯度下降法更新对应的参数（w，b）。

（3）然后继续重复这一过程：

• 恢复被删掉的神经元（此时被删除的神经元保持原样，而没有被删除的神经元已经有所更新）
• 从隐藏层神经元中随机选择一个一半大小的子集临时删除掉（备份被删除神经元的参数）。
• 对一小批训练样本，先前向传播然后反向传播损失并根据随机梯度下降法更新参数（w，b） （没有被删除的那一部分参数得到更新，删除的神经元参数保持被删除前的结果）。

不断重复这一过程。

Dropout在测试时需要怎么补偿？

Dropout代码层面的一些公式推导及代码实现思路：

（1）在训练模型阶段

无可避免的，在训练网络的每个单元都要添加一道概率流程。

图：标准网络和带有Dropout网络的比较

对应的公式变化如下：

• 没有Dropout的网络计算公式：

• 采用Dropout的网络计算公式：

上面公式中Bernoulli函数是为了生成概率r向量，也就是随机生成一个0、1的向量。

代码层面实现让某个神经元以概率p停止工作，其实就是让它的激活函数值以概率p变为0。比如我们某一层网络神经元的个数为1000个，其激活函数输出值为y1、y2、y3、......、y1000，我们dropout比率选择0.4，那么这一层神经元经过dropout后，1000个神经元中会有大约400个的值被置为0。

注意： 经过上面屏蔽掉某些神经元，使其激活值为0以后，我们还需要对向量y1……y1000进行缩放，也就是乘以1/(1-p)。如果你在训练的时候，经过置0后，没有对y1……y1000进行缩放（rescale），那么在测试的时候，就需要对权重进行缩放，操作如下。

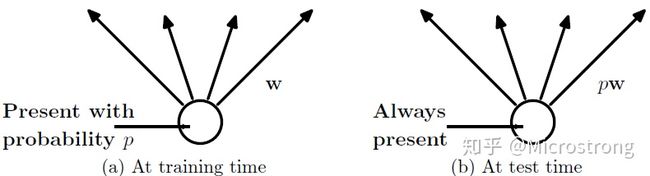
（2）在测试模型阶段

预测模型的时候，每一个神经单元的权重参数要乘以概率p。

图：预测模型时Dropout的操作

测试阶段Dropout公式：

为什么说Dropout可以解决过拟合？

（1）取平均的作用： 先回到标准的模型即没有dropout，我们用相同的训练数据去训练5个不同的神经网络，一般会得到5个不同的结果，此时我们可以采用 “5个结果取均值”或者“多数取胜的投票策略”去决定最终结果。例如3个网络判断结果为数字9，那么很有可能真正的结果就是数字9，其它两个网络给出了错误结果。这种“综合起来取平均”的策略通常可以有效防止过拟合问题。因为不同的网络可能产生不同的过拟合，取平均则有可能让一些“相反的”拟合互相抵消。dropout掉不同的隐藏神经元就类似在训练不同的网络，随机删掉一半隐藏神经元导致网络结构已经不同，整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合，一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。

（2）减少神经元之间复杂的共适应关系： 因为dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用，阻止了某些特征仅仅在其它特定特征下才有效果的情况 。迫使网络去学习更加鲁棒的特征 ，这些特征在其它的神经元的随机子集中也存在。换句话说假如我们的神经网络是在做出某种预测，它不应该对一些特定的线索片段太过敏感，即使丢失特定的线索，它也应该可以从众多其它线索中学习一些共同的特征。从这个角度看dropout就有点像L1，L2正则，减少权重使得网络对丢失特定神经元连接的鲁棒性提高。

（3）Dropout类似于性别在生物进化中的角色：物种为了生存往往会倾向于适应这种环境，环境突变则会导致物种难以做出及时反应，性别的出现可以繁衍出适应新环境的变种，有效的阻止过拟合，即避免环境改变时物种可能面临的灭绝。

6.CNN的平移不变怎么体现？

平移不变性/平移同变性

在欧几里得几何中，平移是一种几何变换，表示把一幅图像或一个空间中的每一个点在相同方向移动相同距离。比如对图像分类任务来说，图像中的目标不管被移动到图片的哪个位置，得到的结果（标签）应该是相同的，这就是卷积神经网络中的平移不变性。

平移不变性意味着系统产生完全相同的响应（输出），不管它的输入是如何平移的 。平移同变性（translation equivariance）意味着系统在不同位置的工作原理相同，但它的响应随着目标位置的变化而变化 。比如，实例分割任务，就需要平移同变性，目标如果被平移了，那么输出的实例掩码也应该相应地变化。一个像素在某一个实例中可能是前景，但是在相邻的一个实例中可能就是背景了，也就是说，同一个像素在不同的相对位置，具有不同的语义，对应着不同的响应，这说的也是平移同变性。

卷积神经网络的平移不变性

平移不变，意思是一只猫头不管在图片的那个位置，cnn都能捕捉到猫头。

简单地说，卷积+最大池化约等于平移不变性。

• 卷积：简单地说，图像经过平移，相应的特征图上的表达也是平移的。下图只是一个为了说明这个问题的例子。输入图像的左下角有一个人脸，经过卷积，人脸的特征（眼睛，鼻子）也位于特征图的左下角。假如人脸特征在图像的左上角，那么卷积后对应的特征也在特征图的左上角。 （如下两幅图所示）

  

• 池化：比如最大池化，它返回感受野中的最大值，如果最大值被移动了，但是仍然在这个感受野中，那么池化层也仍然会输出相同的最大值。再比如平均池化，对于mean来说除非整个感受野内的值都发生同向的剧烈变动，不然mean出啦的值也不会差别那么大。

       所以这两种操作共同提供了一些平移不变性，即使图像被平移，卷积保证仍然能检测到它的特征，池化则尽可能地保持一致的表达。

       卷积的平移不变性就是通过卷积+池化以后不管某一特征移动了位置，总可以检测出来输入到下一层中，又由于全连接是加权求和计算，被激活的特征又可以传导到下一层中。

7.为什么CNN比DNN在图像领域更具优势？

对于图像分类任务，相对于全连接的DNN，CNN模型的主要优点有哪些？_Data+Science+Insight的博客-CSDN博客_cnn模型的优势

【深度学习基础知识 - 40】CNN为什么比DNN在图像领域更具优势_雁宇up的博客-CSDN博客_cnn比dnn好在哪里

DNN,CNN和RNN优缺点/区别_猫不吃老鼠的博客-CSDN博客_rnn缺点

DNN的输入是向量形式，并未考虑到图像的结构信息，没有像素的排列方式的先验知识。每一层都会做一个全局的特征提取，但是由于这个过程并非递进的，因此最终的特征质量并不好，因此难以在图像领域发挥出优势。CNN模型输入的一般都是图像矩阵，然后通过卷积操作进行特征提取，每次卷积都会考虑特征的上下文信息，CNN的架构嵌入了此先验知识。并且随着模型的加深，从浅层提取的局部特征不断地处理、整合得到深层的高维特征。较低的层通常在图像的较小区域中标识特征，而较高的层将较低层的特征组合为较大的特征。在这个过程中，特征的整合是缓慢有序发生的。这对大多数自然图像都能很好地工作，从而使CNN与DNN相比具有领先优势。 

图像通过卷积操作后仍然保留原先的位置关系，当CNN学会了可以检测到特定特征的内核后，便可以在图像中的任何位置检测到该特征。相反，当DNN在一个位置学习某个特征时，它只能在该特定位置检测到它。

因为连续的层仅部分连接并且由于其大量复用权重，所以CNN的参数比全连接的DNN少得多，这使其训练速度快得多，降低了过拟合的风险，并且需要的训练数据也少得多。

由于图像通常具有非常重复的特征，因此对于CNN而言，使用较少的训练实例，可以比DNN更好地泛化图像处理任务（例如分类）。

8.预训练

Frozen：冷冻，冰冻。
Fine-Tuning：微调，更好的对参数进行调整使得更适应当前任务。

预训练的好处

• 训练数据较少时, 难以训练复杂网络。
• 加快训练任务的收敛速度。
• 初始化效果好，有利于优化 。

什么是预训练

在CV里，网络底层参数使用其它任务学习好的参数，高层参数仍然随机初始化。之后，用该任务的训练数据训练网络，底层参数微调。