神经网络丨BP算法(案例代码实现)
下面的代码是利用矩阵的知识点做的,如果学过矩阵论,下面的代码应该比较容易理解。本文内容来源于B站up主东方耀888,视频讲解非常简单易懂,跟着敲一遍就会了。
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
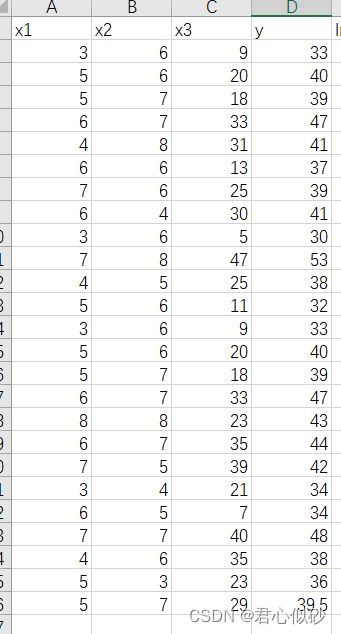
df = pd.read_excel('C:/Users/Dell/Desktop/郑佳重要/不确定理论/liuhuigui.xlsx')
x = df[['x1','x2','x3']]
y = df[['y']]
#归一化处理
x_scaler = MinMaxScaler(feature_range=(-1,1))
y_scaler = MinMaxScaler(feature_range=(-1,1))
x = x_scaler.fit_transform(x)
y = y_scaler.fit_transform(y)
#对样本数据进行转置
sample_in = x.T
sample_out = y.T
#网络参数bp
max_epochs = 1000 #迭代次数
learn_rate = 0.035
mse_final = 6.5e-4 #结束条件
sample_number = x.shape[0]
input_number = 3
output_number = 1
hidden_unit_number = 3 #隐层神经元个数,可更改
#学习 训练 超级参数
#3*3矩阵
w1 = 0.5 * np.random.rand(hidden_unit_number,input_number) - 0.1
#1*3矩阵
w2 = 0.5 * np.random.rand(output_number,input_number) - 0.1
#3*1矩阵
b1 = 0.5 * np.random.rand(hidden_unit_number,1) - 0.1
#1*1矩阵
b2 = 0.5 * np.random.rand(output_number,1) - 0.1
def sigmoid(z):
return 1.0/(1 + np.exp(-z))
#计算误差
mse_history = []
for i in range(max_epochs):
#隐层输出,就是前文里面的outh1
hidden_out = sigmoid(np.dot(w1, sample_in) + b1)
#前文的y
network_out = np.dot(w2, hidden_out) + b2
#误差
err = sample_out - network_out
mse = np.average(np.square(err))
mse_history.append(mse)
if mse < mse_final:
break
#bp反向传播,求偏导的过程
delta2 = -err
delta1 = np.dot(w2.transpose(), delta2) * hidden_out * (1 - hidden_out)
delta_w2 = np.dot(delta2, hidden_out.transpose())
delta_b2 = np.dot(delta2, np.ones((sample_number, 1)))
delta_w1 = np.dot(delta1, sample_in.transpose())
delta_b1 = np.dot(delta1, np.ones((sample_number,1)))
w2 -= learn_rate * delta_w2
b2 -= learn_rate * delta_b2
w1 -= learn_rate * delta_w1
b1 -= learn_rate * delta_b1
#预测值和真实值对比图
#隐层输出
hidden_out = sigmoid((np.dot(w1, sample_in) + b1))
#输出层输出
network_out = np.dot(w2, hidden_out) + b2
#反转获取实际值
network_out = y_scaler.inverse_transform(network_out.T)
sample_out = y_scaler.inverse_transform(y)
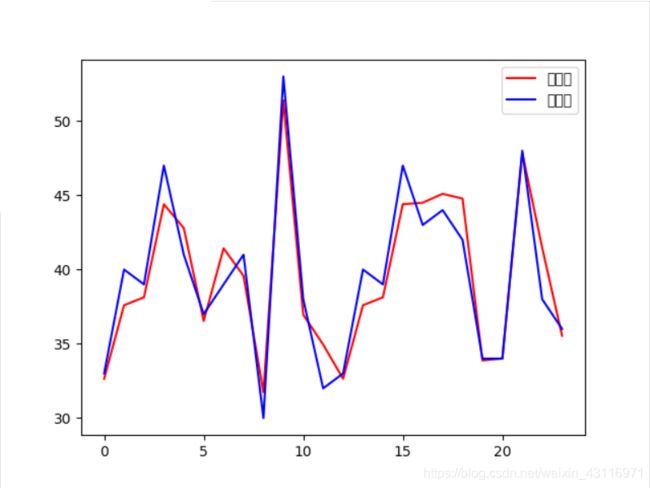
plt.plot(network_out, color="r", label="预测值")
plt.plot(sample_out, color="blue", label="真实值")
plt.legend()
plt.show()看一下拟合后的样子吧,最后还需要使用测试集来计算误差,如果测试集的误差大于训练集,就说明过拟合,想要防止过拟合有几种方法:1、设置正则规则2、增加训练样本数目3、减小模型的参数个数(降维)。
文章中使用到的数据集。